基于IPSO-SVR模型的煤层底板突水量预测

王 鹏，朱希安，王占刚，刘德民

(1.北京信息科技大学 信息与通信工程学院，北京100101；2.华北科技学院 安全工程学院，北京 101601)

0 引言

矿井突水事故严重影响煤矿从业人员生命安全[1]。矿井发生突水事故时，精准地预测煤层底板突水量对于矿井安全生产具有指导作用。目前针对煤层底板突水量的预测有遗传预测法、神经网络预测法、灰色系统理论预测法等多种方法，取得了较好的效果。但如果影响煤层底板突水量的因素发生大幅波动，上述模型的预测误差将会加大：神经网络预测法样本依赖性强；遗传预测法易陷入局部极值。

煤层底板突水量预测中样本量较小且非线性强，支持向量回归机算法(support vector regression，SVR)是较好的解决方法[2]。但在使用SVR模型进行矿井底板突水量的预测中，该模型的惩罚系数C、核函数宽度系数σ和不敏感区域损失函数的宽度ε有随机选取的问题[3]，致使其预测精度低。粒子群算法(particle swarm optimization，PSO)需要调节的参数少，寻优精度高，全局寻优能力强，受到广泛关注。本文提出基于IPSO-SVR(改进的粒子群算法以优化支持向量回归机算法)的煤层底板突水量预测模型，改变粒子群算法的惯性权重因子定义以及引入混沌映射思想，利用改进的粒子群算法对SVR模型的参数(C，σ，ε)进行寻优，实现对突水量的精准预测。

1 IPSO-SVR预测模型整体设计

以王家岭等煤矿的突水点为实例搜集影响煤层底板突水量因素的样本集，对数据进行归一化处理，并按3∶1的比例将样本集分为训练集和测试集。首先初始化改进的粒子群算法种群参数，之后调用SVR算法计算适应度值，迭代寻优得到最佳的SVR模型参数。通过对训练集进行学习建立IPSO-SVR煤层底板突水量预测模型，并对测试集中的数据进行预测，将测试样本结果和实际值进行比较，并分析其绝对误差和相对误差。IPSO-SVR矿井底板突水量预测模型如图1所示。

图1 IPSO-SVR矿井底板突水量预测模型

2 IPSO-SVR模型算法原理

2.1 PSO模型算法

粒子群算法是一种仿生优化算法，经过一定的迭代过程可寻得最优解。在该模型空间中的每个粒子对应一个空间解：li=(li1,li2,…,lin) (i=1,2,…,m)。其中m为空间中粒子的个数，n为某个粒子的维数。粒子的速度记为vi=(vi1,vi2,…,vin)，其速度决定了粒子飞行的方向和距离。标准粒子群算法步骤为：首先初始化粒子的位置和速度，计算每个粒子的适应度函数；每次迭代后计算粒子的个体最优值和群体最优值，并根据式(1)、式(2)更新粒子的位置和速度：

(1)

(2)

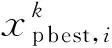
2.2 IPSO模型算法

通过为粒子增加混沌运动、改变粒子的惯性权重因子的定义方式，改变粒子的运动轨迹，加强PSO算法搜索能力、提高算法精度和效率，有效提升SVR模型参数选择能力。

1)根据混沌运动的遍历性，在粒子群算法的每次迭代过程中均可得到一个优化值，将该值与粒子群算法每次迭代所得到的个体最优值进行比较，如果经混沌优化后的值好于标准粒子群算法得到的个体最优值，则用混沌优化后的值代替标准粒子群算法得到的个体最优值。

产生混沌的规则有很多种，如Henon map、Logistic map、Tent map、Ikeda map、Lozi′s等[4]，本文选用遍历性更优的Lozi′s映射的混沌技术方程：

g(k)=1-a|g(k-1)|+d(k-1)

(3)

d(k)=u·g(k-1)

(4)

式中：g(k)∈[0,1]，为混沌变量；k为迭代次数；a为参数，通常取1.7；d(k)代表被映射到优化空间的优化变量；u为参数，通常取0.5。

2)由式(1)可知，粒子的惯性权重因子ω能够影响下一次迭代过程的粒子飞行速度，所以选择一个合适的惯性权重因子可调整算法的搜索能力。若ω值较大，可加强全局搜索能力，避免陷入局部最优；若ω值较小，全局搜索能力变弱，虽然收敛精度变高，但算法易陷入局部最优值。

为加强PSO算法的局部和全局搜索性能，本文将惯性权重因子ω值进行由大到小的线性定义：

(5)

式中：ωmax为惯性权重因子的最大值；ωmin为惯性权重因子的最小值；kmax为设定的最大迭代次数；k为当前迭代次数。

通过动态调整惯性权重因子，IPSO算法能够使粒子在迭代初期进行大范围的搜索。在迭代后期，随着惯性权重因子不断减小，粒子的飞行速度也随之减小，可进行细致的局部搜寻，以免因飞行速度过快而错过最优值。

2.3 SVR模型算法

支持向量机(support vector machine，SVM)是一种基于统计学习理论的机器学习方法，可用于求解回归问题和分类问题。本文使用的支持向量回归机(SVR)是由支持向量机在求解回归问题中的推广[5]。

(6)

式中：w为高维空间中的权重向量；b为阈值；φ(xi)为非线性函数；ε为表示不敏感损失函数宽度的设计参数。

在将低维空间中的样本映射到高维空间并构造线性回归超平面的过程中，引入核函数K(xi，xj)的概念，则可得到回归估计函数：

(7)

式中：αi和αi*为拉格朗日待定系数，求解过程文献[6]作了详尽的解释，本文不再赘述。

由于径向基函数具有较强的泛化能力，故K(xi，x)选取径向基核函数：

(8)

式中σ为核函数的宽度系数。

2.4 IPSO-SVR算法模型

适应度函数的选择体现了优化问题的目标函数与粒子个体适应度值之间的映射关系，该函数选择合适与否决定了算法的收敛速度以及最后的预测精度[7]。结合煤层底板突水量预测问题，本文采用支持向量机中函数复杂性小的不敏感损失函数作为改进的粒子群算法的适应度函数，它表示为能够反映SVR回归性能的均方差：

(9)

式中：m为测试样本个数；y(xi)为i处实际突水量；f(xi)为对i处预测的突水量。

SVR算法的泛化程度受3个重要参数的影响[8]，分别是惩罚系数C、径向基核函数的核函数宽度系数σ和不敏感区域损失函数的宽度ε，这3个参数选取的好坏决定了SVR算法的预测准确度和精度。基于改进的粒子群算法(IPSO)通过迭代寻优找出SVR算法的上述3个参数并预测，IPSO-SVR煤层底板突水量预测模型参数寻优流程如图2所示。

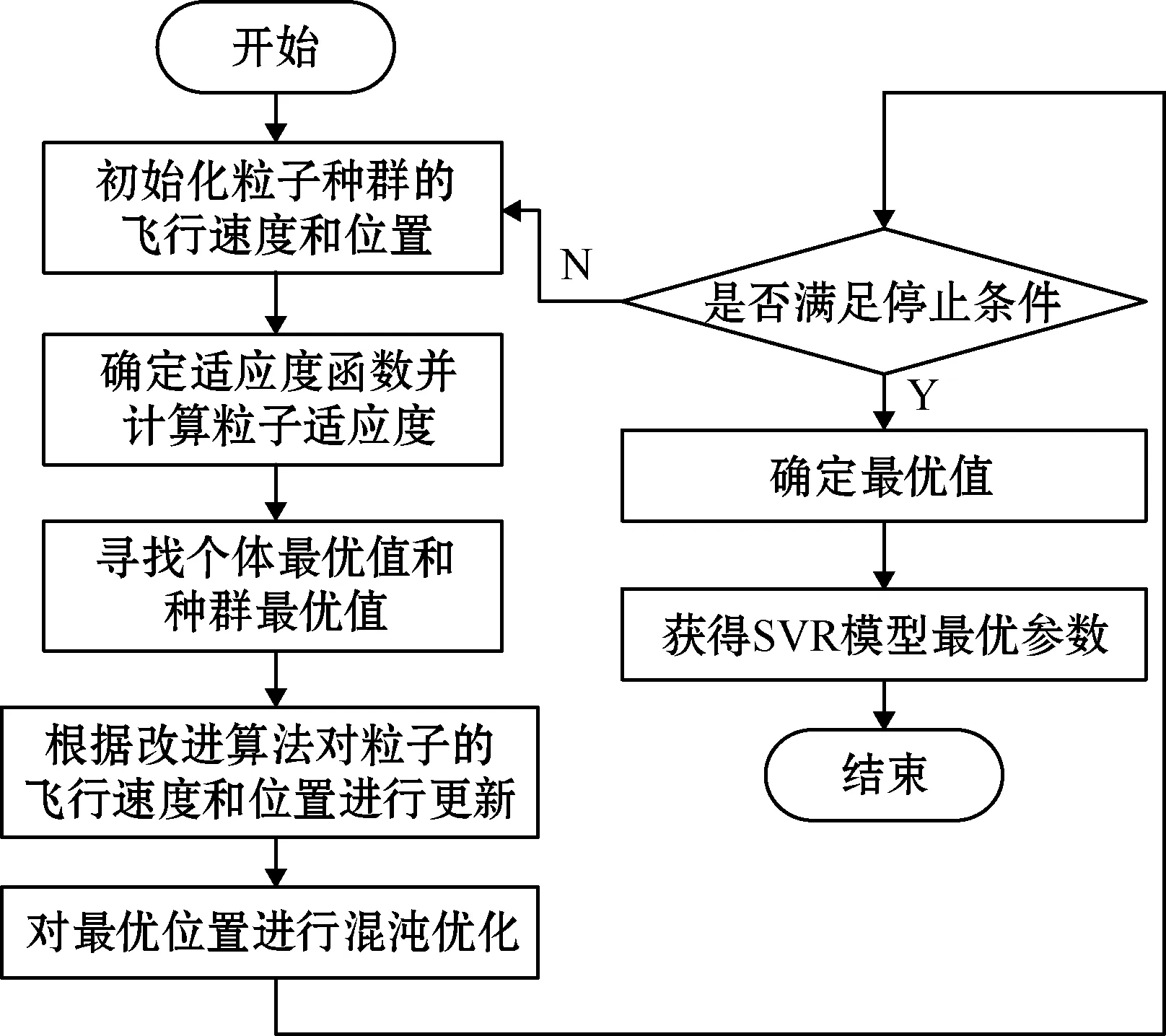
图2 IPSO算法参数寻优流程

3 煤层底板突水量预测实例

3.1 突水因素选取

在煤层底板突水量的预测问题上，需要对影响底板突水量的特征因素进行分析并筛选。以王家岭等矿井突水实际案例为依据，本文选取水压、含水层、隔水层厚度、底板破坏深度和断层落差为特征因素[9]，将这些因素作为煤层底板突水量预测模型的输入向量，输出即为对应工作面突水量的预测值。

3.2 样本集建立

为减小随机因素带来的不稳定差异，本文从实际案例中选取24组数据，将其中18个作为训练样本集，6个作为测试样本集。由于搜集到的影响突水量的数据存在不同的数量级，为消除量纲对实验结果的影响，需要对数据进行归一化预处理[10]，即将数据规范到0～1之间。对于可定量表示的因素用具体值表示；不可定量表示的因素用二值模式表示，例如影响因素的含水层中薄层灰岩用1表示，厚层灰岩用0表示，其余因素则用连续数值表示，对于缺失的值采用平均值代替。归一化方法为

(10)

式中：xmax为单项影响因素数据中的最大值；xmin为单项影响因素数据中的最小值。

经归一化处理后的部分数据集如表1所示。

表1 归一化处理样本集

3.3 参数优化及预测模型建立

为验证改进算法在矿井突水量预测中的可行性，本文基于Matlab环境进行仿真。惯性权重因子的最大值是算法初始值，惯性权重因子的最小值是算法终止值，通常设置最大惯性权重因子ωmax=0.9，最小惯性权重因子ωmin=0.4，最大迭代次数k=200，粒子个数m=40。通过改进的粒子群算法进行参数寻优，多次迭代后可得IPSO-SVR模型的惩罚系数C=72.65，径向基核函数的核函数宽度系数σ=18.516，不敏感区域损失函数的宽度ε=0.128。本文使用此参数进行样本测试集的IPSO-SVR模型煤层底板突水量预测。

3.4 模型验证

本文共设定6个测试样本，利用PSO-SVR模型求出该模型适合的惩罚系数C、径向基核函数宽度系数σ、不敏感区域损失函数宽度ε。分别使用IPSO-SVR模型、PSO-SVR模型进行矿井底板突水量的预测，反归一化后的预测结果如表2所示。该表反映了突水点的实际突水量、IPSO-SVR模型和PSO-SVR模型的预测突水量及这两个模型的绝对误差和相对误差。

从表2可以看出，使用IPSO-SVR模型预测的6组突水点的突水量与使用PSO-SVR模型预测值相比，前者预测值更接近实际值，每个突水点的预测突水量的绝对误差和相对误差也均比PSO-SVR模型明显减小。表明IPSO-SVR模型的预测精度比改进前更高、效果更好，进一步提高了预测的精准度。

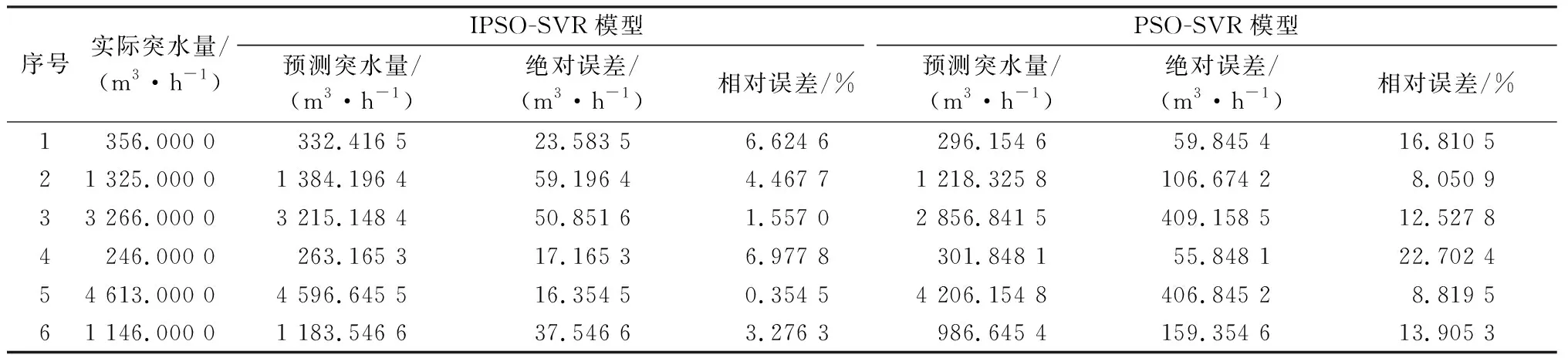
表2 不同模型预测结果精度比较

4 结束语

1) 针对矿井底板突水这种非线性、小样本问题，本文在改进的粒子群算法中提出引入粒子混沌运动和动态改变粒子惯性权重因子的思想，强化了粒子种群的多样性和遍历性，获取支持回归向量机更为精准的惩罚系数、径向基核函数宽度系数、不敏感区域损失函数宽度，避免了参数的人为随机选择问题，建立基于IPSO-SVR的煤层底板突水量预测模型。

2) 结合王家岭煤矿等24个矿井煤层底板突水实例，以水压、含水层、隔水层厚度、底板破坏深度和断层落差为特征因素，使用IPSO-SVR模型和PSO-SVR模型进行突水量的预测。预测结果表明IPSO-SVR模型较改进前预测效果更好，有效强化了算法的全局搜索、提高了算法精度。该模型可以应用于煤层底板突水量预测研究，有助于进行辅助决策，减少矿井中的人员伤亡和财产损失。