基于3DCNN的锅炉再热器管壁减薄预测

闫佳瑛，朱希安

(北京信息科技大学 信息与通信工程学院，北京 100101)

0 引言

锅炉受热面管壁长期处于复杂恶劣的工作环境，易发生腐蚀和泄漏现象，导致发电机组的事故主要集中于锅炉受热管[1-2]。不同学者通过对锅炉受热面腐蚀情况的研究，针对腐蚀原因提出一系列防腐蚀措施，但腐蚀现象仍然是不可避免的[3-4]。

为减少锅炉事故的发生，对受热管壁进行剩余寿命评估非常必要，而剩余寿命评估需要掌握管壁减薄情况。杨淑海[5]采用远场涡流法对管壁厚度进行了检测。于宝虹等[6]采用超声波法对高炉喷煤管道的壁厚减薄情况进行了分析。牟彦春等[7]提出超声相控阵技术对电站锅炉管道进行检测。但上述涡流法及超声波法的实施都需要凭借历史经验安排停机检测，耗费大量的时间成本。

随着电力工业的调整升级和锅炉设备日趋智能化的发展，海量的锅炉运行数据得以累积。通过预测模型结合历史数据对管壁厚度变化趋势进行预测已成为当下的研究趋势。王文辉[8]采用广义回归神经网络对油气管道腐蚀程度进行预测；吴庆伟等[9]利用支持向量机的方法预测了输油管壁厚度的减薄速率。本文以锅炉历史运行数据作为输入，结合3DCNN建立管壁厚度预测模型，对锅炉的管壁减薄情况进行预测。

1 三维卷积神经网络

3DCNN基本结构包括卷积层、池化层、全连接层和输出层。卷积层主要功能是提取锅炉数据的时间维度信息，保证时间连续数据的关联信息不被丢弃，提取时间和空间维度上都具有区分性的特征。经卷积层处理后的数据直接进入池化层，通过池化层可以在缩减数据规模的同时保留有效特征信息，降低训练难度，提高全连接层和输出层的处理速度和预测精度。

1.1 卷积层

卷积层采用3D卷积运算，将时间维度信息作为数据的一个维度。3DCNN卷积层中的运算如图1所示。

在该层中卷积核按照指定步长对输入矩阵进行卷积操作，并且利用激活函数获取卷积操作后的非线性特征，其数学式为

+bij

(1)

1.2 池化层

卷积运算后得到的特征维数较高，为了减小计算量规模，同时为了增强网络的不变性，需要对数据进行池化。池化运算使得特征立方体在时间维度上具有一定的不变性，在保证数据特征的前提下大大减小了计算量。池化的计算式为

(2)

式中：u为三维输入向量；v为经过三维池化操作后的输出；(s,t,r)为坐标上(x,y,z)三个方向上的采样步长；S为采样区域大小。

1.3 全连接层

全连接层类似于传统的人工神经网络，该层中的每个神经层与其前一层的所有神经元进行全连接。全连接层能够整合卷积层和池化层中具有类别区分性的局部信息。

2 数据准备

2.1 数据来源

本文数据来源于神华集团某电厂两台660 MW的超临界机组，具有一定的普适性。以该机组锅炉再热器为试验对象，该机组锅炉的再热器测点布置于尾部竖井中，与烟气成逆流布置，共110组受热面，沿炉膛宽度均匀分布，每组受热面有9根管子。

选取1号机组2017年5～11月的运行数据及2号机组2018年2～8月运行数据进行分析研究。每台机组的再热器管组有100个测点，共有200组数据。但由于传感器失效及失效换管的情况，最终有效测点数据共有192组。1号锅炉部分样本位置及厚度测量如表1所示。

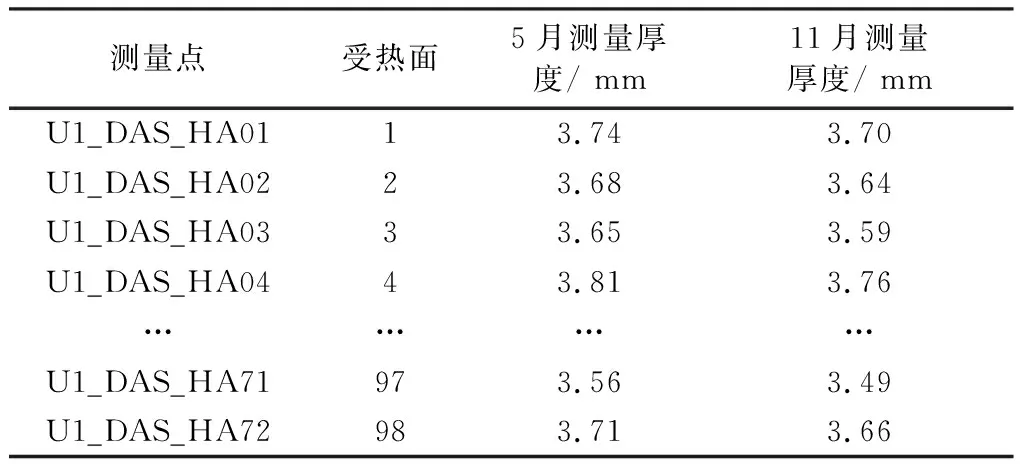
表1 部分测点点号及所在位置

2.2 输入数据选择

本文以锅炉再热器数据为研究对象，再热器的主要功能是将汽轮机排汽重新加热成再热蒸汽，提高电厂循环热效率。影响再热器管壁减薄程度的因素主要包含管壁材质、飞灰磨损及腐蚀[10-12]。

2.2.1 管壁材质

低温再热器管壁材质要适应长期高温高压环境。主要应用材质有20G、25MnG及12CrMoG等。不同材质的制作工艺及化学成分不同，受不同因素影响导致的腐蚀减薄程度也不同。

2.2.2 飞灰磨损

再热器外表面直接接触高温烟气，烟气中存在高速移动的飞灰或未燃尽颗粒，对管壁造成磨损。飞灰的产生原因复杂，与多个锅炉参数有关，包括：入炉煤量、煤质、过剩空气系数、机组负荷、入炉风量。

2.2.3 腐蚀

再热器管壁在长期高温环境下，管壁外侧金属直接与烟气中的氧、硫和碳元素接触，发生不可逆转的物理化学反应。再热器内部流动着具有一定压力的蒸汽，蒸汽在高温催化下会与金属管壁发生反应形成氧化垢，随着高温环境的进一步影响，氧化垢会脱落造成恶性循环。

为防止模型过于复杂，根据以上分析，确定以蒸汽温度、蒸汽压力、负荷、过剩空气系数、蒸汽流量、测点实时温度、排烟温度、给水温度、入炉风量、一次风温及二次风温等11个变量作为外部输入变量。

2.3 数据预处理

由于机组工况复杂，测量设备时常出现故障，导致数据采集不成功，且由于工作环境特殊，出现测量设备故障难以第一时间进行维修，会导致数据出现连续多天的缺失及异常值的出现，为保证时序数据的连续性，本文分别采用中位数补齐的方式填补缺失值；以箱型图对异常值进行筛除，并以中位数补齐方法进行填补。

由于数据样本量纲难以统一，采用归一化的方法对数据进行处理。由于数据每小时更新一次，每天的数据尺寸为24×11，以每180天为一个数据周期，则模型的每个输入样本尺寸为180×24×11。

3 模型设计

3.1 模型搭建步骤

本文在Python环境下搭建3DCNN管壁厚度损失预测模型，以再热器的历史运行数据作为外部输入变量，以管壁实际减薄损失值为因变量。通过对比测试值与真实值的误差，不断调整模型参数，具体步骤如下：

1) 对历史数据进行预处理，分别进行异常值检测与缺失值填补；将每一组样本尺寸处理为180×24×11。

2) 将数据分为训练集和测试集，分别作为3DCNN的输入进行训练和验证，调整模型参数及结构。

3) 以测试集的预测值与真实值之间的平均绝对误差及最大绝对误差为评判标准，评价整体模型的优劣程度。

3.2 模型流程图

基于3DCNN的管壁厚度损失预测模型流程如图2所示。

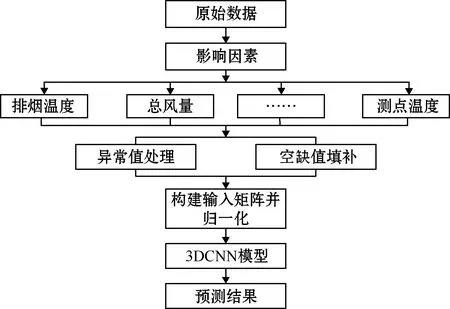
图2 基于3DCNN的管壁厚度损失预测流程

4 试验验证

由于难以根据历史经验设置模型结构参数，需要不断调整参数来找出适合的值。为减少训练的时间成本，最大程度避免过拟合及陷入局部最优等情况，下面讨论卷积核的数目及尺寸两种因素对预测效果的影响，以平均绝对误差及最大绝对误差为评价指标。以随机180组数据作为训练集，以12组数据作为测试集。

4.1 卷积核数目

卷积核个数的增加能够充分提取训练样本中的差别信息，但数目过多会陷入局部最优的误区。本试验在卷积层中分别配置不同的卷积核个数，在不同配置方案下，对预测值与实际值进行比较，试验结果如表2所示。

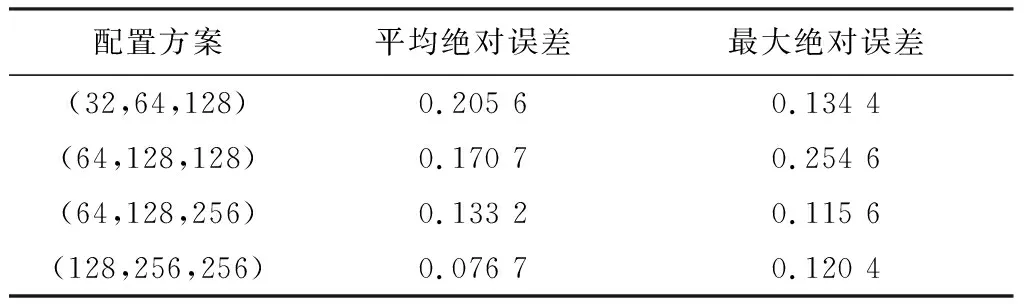
表2 不同卷积核数目的试验结果

由表2可以看出，随着各配置方案中各层卷积数目的增加，平均绝对误差呈下降趋势，在配置方案为(128,256,256)情况下，平均绝对误差最小且最大绝对误差相对较小。故本文配置方案为(128,256,256)形式。

4.2 卷积核尺寸

卷积核的尺寸直接影响特征提取的效果，影响模型的运算速度及效果。将卷积核尺寸分别设置为3×3×3、5×5×5、7×7×7及9×9×9等4种情况。试验结果如表3所示。由表可见，当卷积核尺寸为3×3×3时，预测效果最优。

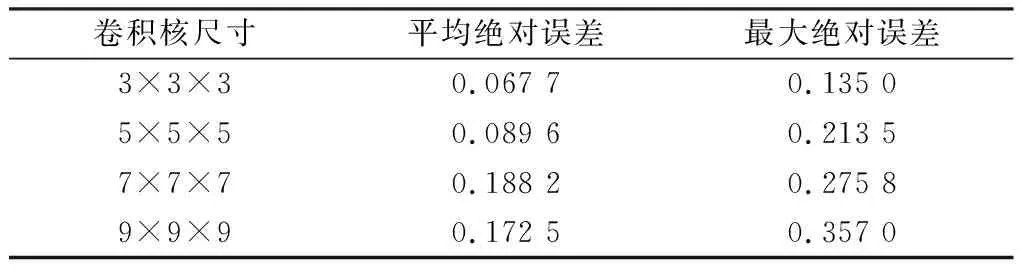
表3 不同卷积核尺寸的试验结果

4.3 模型最终结构

通过上述试验结果及分析，确立3DCNN模型包含3层卷积层，卷积核的步长均为1。模型为保证边界数据信息不丢失均采用SAME的补零方式，加入补零操作后，卷积层的输入维度和输出维度一致。详细结构如表4所示。表中C表示卷积层；S表示池化层；Fc表示全连接层。

表4 3DCNN模型最终结构

4.4 试验结果分析

由训练模型得到的预测结果与真实值的对比情况如表5所示。

表5 测试集结果对比 mm

通过分析试验结果，预测值与实际值最大绝对误差为12.04%，平均绝对误差为6.77%。说明该模型能够通过对历史运行状态的分析预测管壁厚度的变化情况。

5 结束语

本文运用新建的3DCNN模型对再热器管壁厚度减薄情况进行预测，该模型在测试集上的平均绝对误差为6.77%，具有较强的预测功能，可以准确高效地对管壁减薄情况进行预测。

该方法虽然预测效果较好，但存在历史数据庞大、训练模型消耗时间长的缺点，且存在超参数过多的问题，需要进一步研究改进。