针对多振源密频及波动线谱主动控制的改进算法及试验*

李 彦，何 琳 ，王迎春，王春雨，尹天齐

(1. 海军工程大学 振动与噪声研究所， 湖北 武汉 430033；2. 海军工程大学 船舶振动噪声重点实验室， 湖北 武汉 430033)

船舶机械振动含有丰富而突出的线谱成分，这些线谱能量集中、幅值远高于周围频率宽带噪声，且各线谱幅值、频率均会随着机械运转工况而波动。船舶机械振动线谱对船舶辐射噪声有重要影响，机械设备主动隔振技术作为一种抑制线谱的有效手段而日益受到重视。

对船舶机械振动线谱的实测和特征分析表明，为了实现更好的线谱控制效果，机械主动隔振的有源控制算法需要突破以下难点：①有多根线谱振动需要进行控制，采用传统的宽带自适应算法只能有效控制其中最强的1～2个频率振动；②机械设备由多个隔振器支承，结构通常较复杂，次级通道矩阵特征值分散度大，造成收敛稳定性和速度难以兼顾[1]；③机械设备的振幅和频率均可能出现波动，控制算法应具有较快收敛速度并对频率波动具有较好鲁棒性，才能取得良好线谱控制效果；④通常会将多台船舶机械安装在公共浮筏隔振装置上，多台机组同时运转，因此激发处于同一窄带、频率相近但有细微差别的多线谱振动，运转工况波动还可能引起多线谱频率同时波动、引发多振源密频线谱控制难题。

窄带自适应控制算法是在传统宽频自适应算法基础上，针对多线谱控制需求提出的，该类算法[1-3]采用分离提取参考信号和误差信号中不同频率线谱成分，多个控制子系统并行控制多个线谱成分。因此可针对难点①的多根线谱振动(噪声)控制取得良好效果。其中常见的窄带FxLMS算法[1-3]已在精密平台等方面得到了较多应用，但对于机械设备多通道主动隔振系统耦合性复杂的情况，FxLMS算法的次级通道矩阵特征值分散度大，仍存在收敛速度慢、稳定性差的控制难题[1,4]。

针对难点②，海军工程大学的李彦等[4]在Elliott频域多通道Fx-Newton算法[1]的基础上，提出了时域窄带多通道Fx-Newton算法。该算法的收敛速度对多通道耦合特性不敏感，可显著提高机械振动主动控制的收敛速度和稳定性；并且突破了此类算法通常在频域实现的局限性，无须时频变换、可确保实时性。该算法已较好地解决了工程实际中机械设备振动主动控制的多线谱、多通道耦合、收敛速度和稳定性兼顾等技术难题，但仍难以满足线谱频率波动和多振源密频耦合等实船复杂工况下的线谱主动控制需求。

本文在时域窄带多通道Fx-Newton算法(简称“窄带Fx-Newton算法”)优点的基础上，针对难点③的频率波动线谱主动控制需求，研究了窄带滤波相位失真的自适应补偿器，提出了对线谱频率波动具有高鲁棒性的改进算法(简称“相位补偿Fx-Newton算法”)；针对难点④的多振源密频线谱的主动控制需求，研究了从多振源分离提取互不相关的多参考信号，从而实现多振源密频线谱高效、稳定控制的改进算法(简称“多参考Fx-Newton算法”)，并且算法功能模块可以针对工况进行组合调用。

1 算法频域公式

本文研究的相位补偿Fx-Newton算法和多参考Fx-Newton算法是在时域执行的，但考虑到频域分析方法的简洁性和直观性，算法原理公式首先采用频域方法进行推导。

1.1 Fx-Newton算法频域公式

设主动控制系统的作动器和误差传感器的数量都是L。多通道Fx-Newton算法的控制器频响自适应更新公式[4-5]为：

(1)

控制器的最优解[4-5]为：

(2)

更普遍地，对于作动器和误差传感器数量分别为L、K的主动控制系统(K≥L)，多通道Fx-Newton算法的控制器更新公式为：

(3)

控制器的最优解[1, 5]为：

(4)

1.2 相位补偿Fx-Newton算法频域公式

振动信号通常由多个频率分量叠加，频域算法需进行时频变换，故会导致实时性差；而时域算法中，需要提取才能获得单频线谱信号，其中一种方法是辨识频率后采用正弦发生器输出单频参考信号[6]，但该算法对频率失配(估计频率与实际频率有偏差)的鲁棒性较差[7]。

通常采用窄带带通滤波器(以下简称“窄带滤波器”)提取单频线谱信号[1,4]，其优点是无须估计频率，提取的信号频率与原信号一致。

窄带Fx-Newton算法频域原理如图1所示。设窄带滤波器在频率ω处频响为复数B，滤波前的参考信号、扰动信号和误差信号在频率ω处的频谱分别为Xo，Do和Eo，滤波后的信号X=BXo，D=BDo，E=BEo，控制信号Y=WX。

图1 含窄带滤波器的Fx-Newton算法频域原理Fig.1 Frequency-domain schematic diagram of Fx-Newton algorithm with narrowband-pass filter

窄带Fx-Newton算法频域迭代公式[4-5]为：

(5)

其中，R为次级通道广义逆模型滤波后的参考信号频谱。

(6)

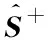
但对于机械运转频率在一定范围波动的情况，控制器最优系数为：

Wopt=-B-1S+X-1D=-B-1S+(Xo)-1Do

(7)

频率波动会使相频响应陡峭的滤波器出现较大波动，从而导致最优解Wopt本身不断波动，影响寻优控制效果。

针对线谱频率波动，研究了窄带滤波相位失真的自适应补偿器，用于抑制线谱频率波动时由窄带滤波环节引起的最优解波动，从而提高主动控制的鲁棒性。

相位补偿Fx-Newton算法频域原理如图2所示。设相位差补偿器在ω处频响为复数C、串联在窄带滤波器之后，有X=CBXo。若补偿器频响为C=B-1，则有Wopt=-S+(Xo)-1Do，可使Wopt不受窄带滤波器频响特性影响。

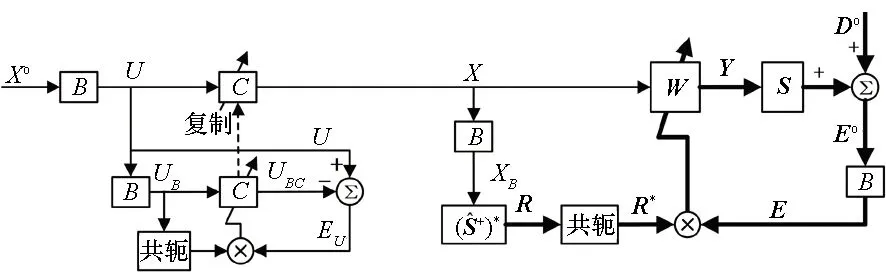
图2 相位补偿Fx-Newton算法频域原理Fig.2 Frequency-domain diagram of the Fx-Newton algorithm with phase-shift compensator

该相位差补偿器的频响C需随ω波动而调整，采用一个在线自适应调整环节实现，并与控制子系统相对独立，如图2所示。U=BXo，UB=BU，UBC=CUB，则有：

EU=U-UBC=U-CUB

(8)

(9)

(10)

其中，JU为性能函数，gU为其相对于C的梯度。

因此相位差补偿器的频域迭代公式为：

(11)

其中，ε为收敛步长。式(11)为单通道LMS算法，无须调用控制系统次级通道和控制器系数，不受隔振装置物理特性影响，运算量小、收敛速度快。当ω波动时，式(11)快速收敛，使EU→0，CBU→U，从而保持C→B-1。

1.3 多参考Fx-Newton算法频域公式

在船舶中常将多台机械安装在公共浮筏上，可能激发处于同一窄带、频率相近但有细微差别的多线谱振动，本文以同一窄带的双线谱控制为例进行研究。

由于误差信号中的窄带双谱很难分离，采用同一个控制器对窄带双线谱进行控制很困难。但根据自适应控制的相关性特性，若能从两个振源分别获得两个参考信号[8-9]，并确保参考信号与对应振源相关性较强、与另外振源相关性较弱，然后将两个参考信号分别输入两个并行控制器，则即使误差信号中同时含有两个振源引起的振动，也可取得较好控制效果。

在能获得独立参考信号的前提下，本文的多参考Fx-Newton算法频域原理如图3所示。在实际应用中，多台机械振源的独立参考信号可以是旋转机械的转速信号、往复机械的脉冲信号、机脚加速度信号等。

图3 双参考Fx-Newton算法频域原理Fig.3 Frequency-domain diagram of the double-reference Fx-Newton algorithm

图3中变量定义与图1中一致，区别在于顶标“—”对应第二个振源，不带顶标则对应第一个振源。

经窄带滤波后，双线谱密频误差信号为：

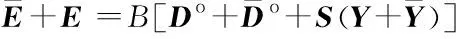
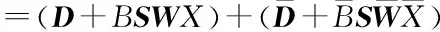
(12)

控制算法的性能函数为：

(13)

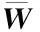
(14)

(15)

由此可得，双参考Fx-Newton算法频域迭代公式为：

(16)

(17)

其中，

(18)

(19)

2 算法时域实现

2.1 相位补偿Fx-Newton算法的时域实现

图4 线谱频率ω处的2阶时频滤波器Fig.4 The 2nd-order time-frequency filter for sinusoid at frequency ω

对于相位补偿Fx-Newton算法，图2中的相位差补偿器在时域实现的结构如图5所示，同样基于2阶时频滤波结构进行相位补偿滤波。补偿器的实部系数cR和虚部系数cI参照频域式(8)和式(11)进行时域迭代调整。图5中时域信号u(n)与图2中频域信号U的实部成分相对应，而uQ(n)与u(n)正交，对应频域信号U的虚部成分，后续其他信号e(n)、d(n)等定义均可依此类推。

图5 窄带滤波相位差的自适应补偿器结构Fig.5 Adaptive phase-shift compensator for the narrowband pass filtering in time domain

2.2 多参考Fx-Newton算法的时域实现

对于多参考Fx-Newton算法，图3的频域原理框图在时域实现的结构如图6所示(以双参考、1个窄带频段、具有3个误差传感器和2个作动器的系统为例)。从图6中可知，首先应对双振源的参考信号分别进行提取、相位差补偿、次级通道广义逆模型滤波，其误差信号无须区分，然后进行两个参考子系统的控制器系数更新和控制信号生成，最后将两个子系统控制信号叠加输出。

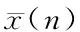
(20)

(21)

图6 多参考Fx-Newton算法时域结构Fig.6 Multi-reference Fx-Newton algorithm in time domain

(22)

最终输出的控制信号为各参考信号子系统的叠加：

(23)

图6中的相位差补偿模块可以针对工况进行组合调用，若实际工作时线谱频率较稳定，可不采用该补偿环节。

3 实验研究

3.1 双振源密频线谱的控制实验

3.1.1 实验台架及测点布置

本实验在双机组浮筏隔振装置上进行，如图7所示，浮筏上共安装有两台空气压缩机组，各由12只橡胶隔振器支撑，筏架与基座之间由6个气囊隔振器连接，总承载约5 t。6个气囊隔振器内集成有磁悬浮作动器(称为作动器A1～A6)，作为主动控制次级振源；以基座6个主被动隔振器附近的加速度为误差信号(称为测点e1～e6)。

图7 浮筏隔振装置的主动作动器及测点布置Fig.7 Experimental setup of active actuators and measuring points for the raft isolation device

两台空气压缩机组运转可激发宽频与多根线谱振动。此外，浮筏上表面的前部和后部共安装有2只电磁惯性振子激振器(分别称为激振器1和2)，也可作为初级振源输出较理想的窄带双线谱信号。

3.1.2 激振器输出窄带双线谱时控制效果对比

通过惯性激振器激发频率相近、处于同一个窄带频段的双线谱振动(60 Hz与62 Hz)。采用单参考Fx-Newton算法进行两组实验，然后采用多参考Fx-Newton算法进行第三组实验。其中，第一组实验的参考信号为激振器1激励电压(称为ref 1)，包含62 Hz成分；第二组实验的参考信号为中层筏架加速度信号(称为ref 2)，包含60 Hz与62 Hz成分；第三组实验的双参考信号分别为两个激振器的激励电压。

图8(a)为参考信号ref 1的Fx-Newton算法控制过程中误差测点振动时频谱图(基于短时傅里叶变换(Short-Time Fourier Transform,STFT))，可知该算法难以同时抑制同一窄带频段的双线谱振动，仅对其中一根线谱有抑制效果，因为其参考信号仅包含与一个振源相关的成分。图8(b)为参考信号ref 2的Fx-Newton算法试验结果，其参考信号同时包含60 Hz与62 Hz成分，不仅没有取得线谱抑制效果，而且还导致同一窄带频段的双线谱振动控制发散了。试验结果表明，用单参考Fx-Newton算法难以控制多个振源引发的窄带多线谱振动。

(a) 采用62 Hz单参考信号(ref 1)(a) Single-reference with 62 Hz(ref 1)

(b) 采用60 Hz与62 Hz叠加单参考信号(ref 2)(b) Single-reference with 60 Hz and 62 Hz(ref 2)图8 单参考Fx-Newton算法控制的误差测点短时傅里叶时频谱Fig.8 Evolution of the average STFT power spectra of the error signals for the Fx-Newton algorithm with single reference

图9为双参考Fx-Newton算法的误差测点振动时频谱图，两根线谱都被迅速、有效控制，最终被淹没于背景噪声，说明本文算法对同一窄带频段双线谱振动取得了很好的控制效果。

图9 双参考Fx-Newton算法控制的误差测点振动时频谱Fig.9 Evolution of the average power spectra of the error signals for the double-reference Fx-Newton algorithm

该算法的控制信号为各参考信号子系统的控制信号叠加，因此若能获得独立参考信号，该算法可适用于三个及更多振源的主动控制。

3.1.3 两台空压机组运转激励窄带双线谱时的控制效果

在实验装置上，让两台空压机组同时运转，转速约1500 r/min，基频约25 Hz，各次谐频分别为50 Hz、75 Hz等。首先在不进行主动控制的情况下采集250 s数据分析其振动特性，图10(a)为双机组同时运转时基座测点75 Hz附近振动时域波形，可知振幅忽高忽低，幅值呈现周期性的强弱变化，即出现了“拍”的现象，这是因为两台空压机组的转速很接近但又有轻微差别，从而引发了窄带密频双线谱振动。图10(b)为基座e1～e6测点平均功率随时间变化曲线，更直观地呈现振动功率周期性强弱变化。

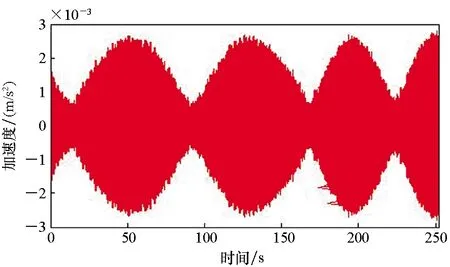
(a) 误差测点75 Hz振动的时域数据(a) Time domain record of the error signal at 75 Hz

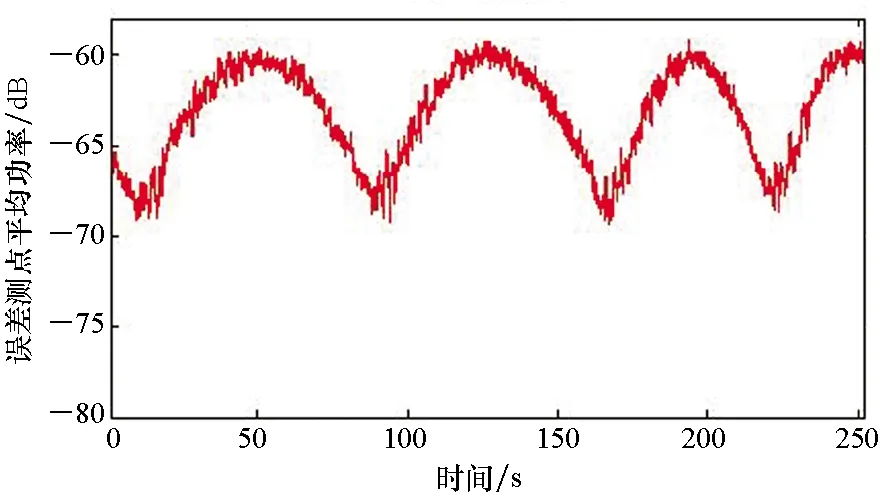
(b) 误差测点75 Hz振动功率随时间变化过程(b) Evolution of the average power of the error signals at 75 Hz图10 不进行主动控制时，误差测点75 Hz振动时域波形及功率Fig.10 Time domain record and evolution of average power of the error signals at 75 Hz without active control

然后采用双参考Fx-Newton算法进行主动控制(双参考信号分别为两台空压机的机脚振动)，实验结果如图11所示。

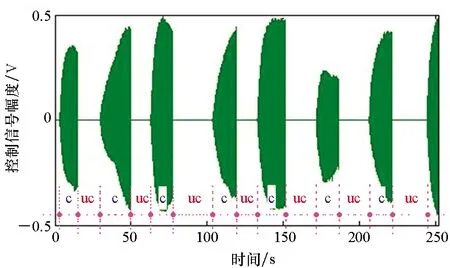
(a) 控制信号时域波形(a) Time domain record of the error signal

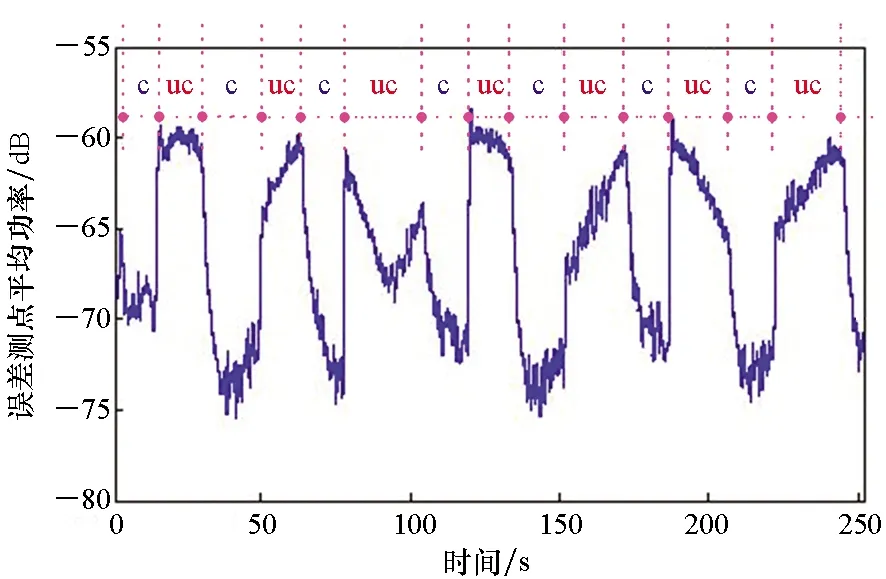
(b) 误差测点75Hz振动功率随时间变化过程(b) Evolution of the average power of the error signals at 75 Hz图11 主动控制开启/关闭时，控制信号时域波形及误差测点75 Hz振动功率Fig.11 Time domain record of control signal and the evolution of average power of error signals at 75 Hz with active control on/off

考虑到“拍”现象导致的振幅强弱变化，每隔10～20 s开启/关闭主动控制算法以便于对比观察控制/不控制状态下的振动功率差别。图11(a)为控制信号时域波形，可明确区分控制/不控制状态的分段，分别标记为“c”和“uc”，并相应地将图11(b)基座误差测点平均振动功率曲线也分成控制/不控制的14个分段。观察图11(b)并对比图10(b)可知，本文提出的多参考Fx-Newton算法效果非常好，可对两台空压机组运转激励的窄带密频双线谱振动进行有效抑制，一旦切换到“控制状态”，则基座误差测点振动迅速降低，控制效果达到14 dB左右。

3.2 频率波动线谱的控制实验

3.2.1 实验台架及测点布置

本实验在如图12所示的单层隔振装置上进行，上层平台与基座之间由6个气囊隔振器连接，总承载约3.6 t。6个气囊内集成有磁悬浮作动器(称为作动器A1～A6)，作为主动控制的次级振源；以基座6个主被动隔振器附近的加速度为误差信号(称为测点e1～e6)。上层平台安装有电磁惯性振子激振器作为初级振源，输出频率波动的扫频线谱振动。

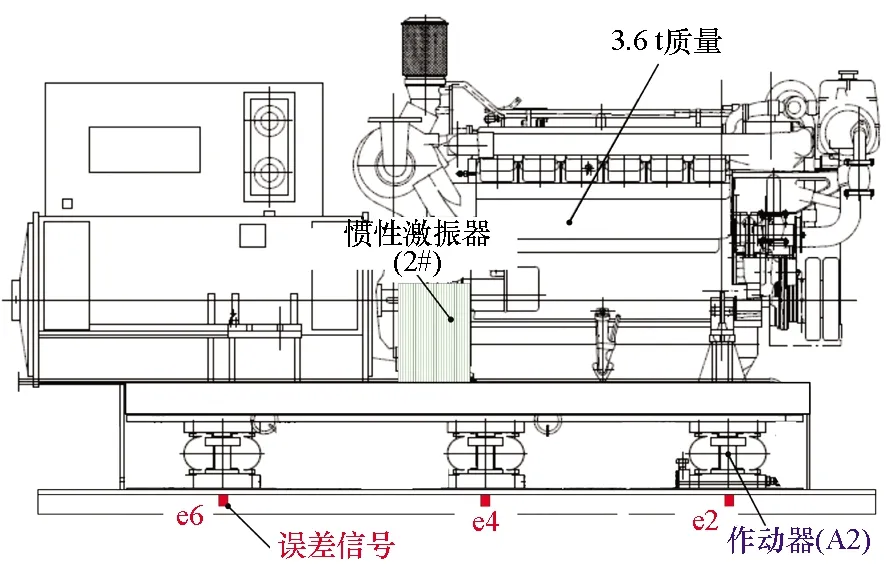
图12 单层隔振装置的主动作动器及测点布置Fig.12 Experimental setup of active actuators and measuring points for the single-layer isolation device

3.2.2 单激振器输出频率波动线谱时控制效果对比

以激振器1#作为初级振源，输出扫频线谱，在频率fo-2.5 Hz到fo+2.5 Hz之间线性扫描，扫频速度0.2 Hz/s，采用Fx-Newton算法和相位补偿Fx-Newton算法分别进行主动控制，参考信号为惯性激振器动子加速度，实测对比两种算法对频率波动线谱的控制效果，结果如图13～14所示。

对比图13(a)和图13(b)时频谱图(6个误差测点平均)可知，在中心频率fo=80 Hz扫频工况下，采用Fx-Newton算法控制后，由于频率波动导致窄带提取的参考信号相位剧烈波动，引起最优控制系数波动，控制算法难以寻优，因此线谱功率有一定降低，但效果不够明显；而采用相位补偿Fx-Newton算法后，其相位补偿环节可以抑制窄带参考信号的相位波动，使最优控制系数稳定，控制后的线谱功率降低到更接近背景噪声水平；从图13(c)可知，相位补偿Fx-Newton算法对扫频线谱的控制效果改善了约15 dB。从图14可知，中心频率fo=110 Hz扫频工况下的主动控制试验也有类似结果，相位补偿Fx-Newton算法控制效果提高约13 dB。

(a) Fx-Newton算法(a) Fx-Newton algorithm

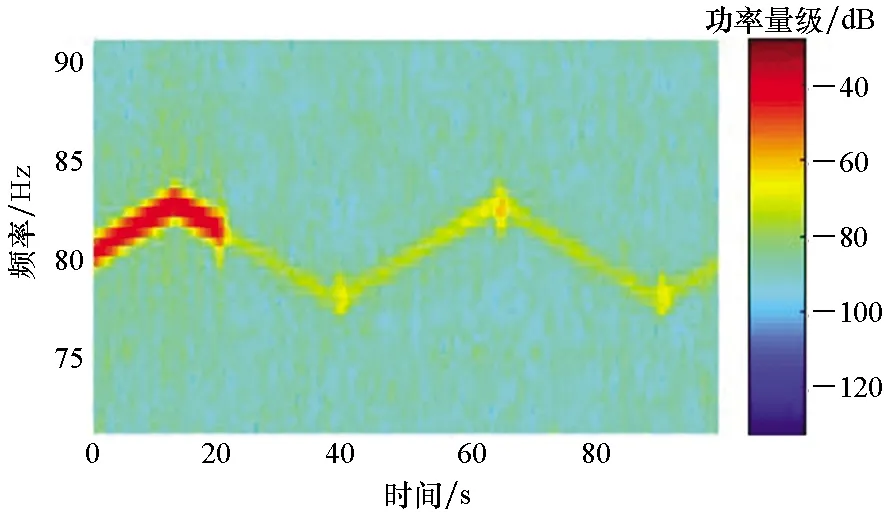
(b) 相位补偿Fx-Newton算法(b) Fx-Newton algorithm with phase-shift compensator

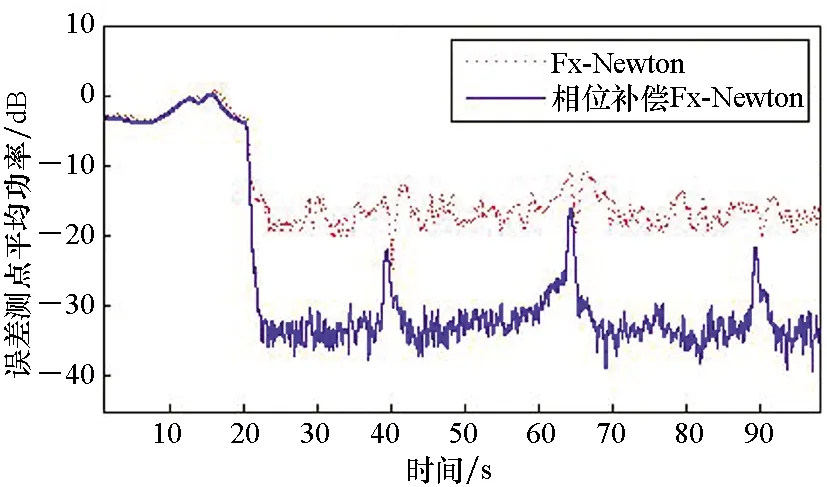
(c) 两种算法对比(c) Comparison of two algorithms图13 fo=80 Hz时，无/有相位补偿的Fx-Newton算法的误差信号功率收敛过程 Fig.13 Evolution of the average power spectra of the error signals for the Fx-Newton algorithm with and without phase-shift compensator when fo=80 Hz

(a) Fx-Newton算法(a) Fx-Newton algorithm

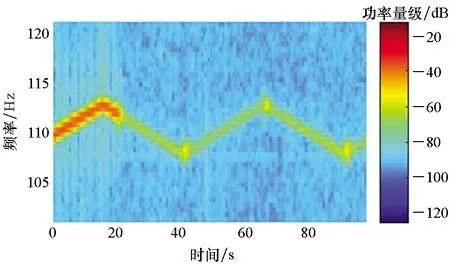
(b) 相位补偿Fx-Newton算法(b) Fx-Newton algorithm with phase-shift compensator

(c) 两种算法对比(c) Comparison of two algorithms图14 fo=110 Hz时，无/有相位补偿的Fx-Newton算法的误差信号功率收敛过程 Fig.14 Evolution of the average power spectra of the error signals for the Fx-Newton algorithm with and without phase-shift compensator when fo=110 Hz

图15为中心频率fo=80 Hz扫频、然后频率往复突变工况下的实验结果。可知Fx-Newton算法和相位补偿Fx-Newton算法在线谱频率跳变后，均未出现不稳定发散问题；频率跳变后，两种算法均出现了很短时间(<0.5 s)的超调，其中相位补偿Fx-Newton算法由于补偿环节的存在，超调量比Fx-Newton算法高约2 dB，但是后续两种算法均能重新快速收敛、恢复控制效果，鲁棒性好；相位补偿Fx-Newton算法控制效果仍远优于Fx-Newton算法。

(a) Fx-Newton算法(a) Fx-Newton algorithm

(b) 相位补偿Fx-Newton算法(b) Fx-Newton algorithm with phase-shift compensator

(c) 两种算法对比(c) Comparison of two algorithms图15 fo=80 Hz时，扫频且频率突变工况下，无/有相位补偿的Fx-Newton算法误差信号功率收敛过程Fig.15 Evolution of the average power spectra of the error signals for the Fx-Newton algorithm with and without phase-shift compensator, when fo=80 Hz and frequency sweeps and jumps

3.3 频率波动双振源密频线谱的控制实验

以激振器1#和2#作为两个初级振源，输出同一窄带内的双扫频线谱，采用具有相位补偿功能的双参考Fx-Newton算法进行主动控制，参考信号为两个惯性激振器动子加速度。

图16的工况为中心频率fo=80 Hz，两个激振器分别以fo-2.5 Hz和fo+2.5 Hz为起点频率，在fo-2.5 Hz到fo+2.5 Hz之间扫频，速度0.2 Hz/s。从图16可知，在双线谱频率波动反向扫频工况下，本文算法取得了良好控制效果，控制后的线谱基本淹没于背景噪声。

图16 相位补偿双参考Fx-Newton算法的误差信号功率收敛过程Fig.16 Evolution of the average power spectra of the errors for the double-reference Fx-Newton algorithm with phase-shift compensator

图17的工况为中心频率fo=80 Hz，两个激振器分别以fo-2.5 Hz和fo-1.5 Hz为起点频率，以fo+1.5 Hz和fo+2.5 Hz为终点频率，扫频并且频率往复突变。从图17(a)可知，在频率差为1 Hz的密频双线谱同向扫频工况下，本文算法控制后的线谱也基本淹没于背景噪声；在频率跳变后，能重新快速收敛、恢复控制效果，具有很好的稳定性。对比图17(a)和图17(b)可知，扫频速度提高一倍，本文算法控制效果略有下降，但仍较优良，稳定性仍较好。

(a) 扫频速度0.1 Hz/s(a) Swept speed of 0.1 Hz/s

(b) 扫频速度0.2 Hz/s(b) Swept speed of 0.2 Hz/s图17 扫频且频率突变工况下，相位补偿双参考Fx-Newton算法的误差信号功率收敛过程Fig.17 Evolution of the average power spectra of the errors for the double-reference Fx-Newton algorithm with phase-shift compensator, when the frequency sweeps and jumps

4 结论

针对工程实际中机械设备振动线谱频率波动以及多台机组运转激励出密频振动线谱带来的主动控制难题，在前期研究的收敛速度快、稳定性好的多通道窄带Fx-Newton算法基础上进行改进，提出相位补偿Fx-Newton算法和多参考Fx-Newton算法，推导了算法频域公式，给出时域实现公式，并进行了实验研究。

实验结果表明，用单参考Fx-Newton算法难以控制多个振源引发的窄带多线谱振动，而双参考Fx-Newton算法对双激振器、双空压机机组激励出的同一窄带频段双线谱振动都可取得很好的控制效果。相位补偿Fx-Newton算法对于频率波动线谱的控制效果，比Fx-Newton算法提高了13～15 dB，并且在频率突变等情况下具有良好的鲁棒性。本文还将相位补偿与双参考算法结合，进行了频率波动双振源密频线谱的控制实验，也取得了良好的控制效果，进一步验证了控制算法的鲁棒性。