基于最小二乘拟合的无人机运动目标测速方法

2021-04-09郑献民殷少锋林宏旭

兵器装备工程学报 2021年3期

郑锴，郑献民，殷少锋，林宏旭

(中国人民解放军32146部队，河南焦作 454000)

运动目标(如车辆、船艇、装甲集群等)参数已成为全面化和动态化战场态势的要素，是火力武器系统(如远程火箭炮、自行加榴炮等)对运动目标打击的难点问题。运动目标的拦阻射击或精确打击，需要依据运动目标的实时位置和速度等信息来确定射击时机和射击诸元。尤其对于非制导武器或修正能力弱的制导武器，由于发射后无法实时修正或修正有限，如果在发射时不依据目标位置和速度等信息给出修正量，攻击运动目标难以实现。

传统的运动目标侦察设备主要有地面光电侦测设备和活动目标侦察雷达。地面光电侦测设备测量方法，通常为前沿观察所侦察兵利用激光测距机等设备，进行目标定位并人工外推解算，其误差较大、效率较低、难以应用于远程火力；活动目标侦察雷达测量方法，通常为利用多普勒效应进行侦测，其作用范围和测量精度受限。基于无人机光电云台的运动目标参数测量，具有作用范围广、测量精度高、使用灵活、隐蔽性好等优点[1-5]。当前，国内外学者对无人机固定目标定位进行了较为广泛的研究[6-8]，但对无人机运动目标定位和测速的研究较少[1-5]。运动目标定位和测速，受无人机平台和光电云台测量误差、目标运动模式的影响，运动目标参数测量的实时性和高精度是难点问题。现役无人机对运动目标定位和测速的能力较为薄弱，无人机保障火力武器系统对运动目标打击的演练往往难以实施。

无人机运动目标测速方法主要有目标跟踪测速和目标定位测速法[1-5]。目标跟踪测速法是基于目标跟踪和全微分思想进行解算，该方法测速精度和效率较高，但是其要求无人机具备飞机机体和光电云台的姿态角速度、激光测距变化速率等测量信息；目标定位测速法是利用运动目标在不同时刻的位置坐标，通过一定的数据处理方法得到目标速度值，该方法实时性好、易于实现。

由于受系统误差和测量噪声等的影响，数据处理是目标定位测速的关键环节。常用的处理方法有：均值法、最小二乘法、递推最小二乘法、卡尔曼滤波方法、最小二乘拟合法等[9-15]。均值法适用于匀速直线运动，将观测采样点间的距离除以时间求得速度；最小二乘法是基于匀速直线运动模型构建超定方程组，并采用最小二乘法解出速度，在采样非等间隔、机动运动等情况下应用受限；递推最小二乘和卡尔曼滤波方法，均是基于特定运动模型和递推思想进行速度求解，计算较复杂、收敛速度较慢，如果初值选择不当，可能会出现发散情况；最小二乘拟合法是通过构建目标运动轨迹的多项式函数，对轨迹多项式函数求导得到目标的运动速度。

本文提出了一种基于最小二乘拟合的无人机运动目标参数测量方法。该方法的主要流程为：1)通过基于成像模型的共线定位方法，实现序列图像中运动目标的定位解算；2)通过基于最小二乘多项式拟合法，构建运动目标位置、速度和加速度的多项式，求得所需时刻运动目标的位置、速度和加速度等矢量参数。该方法精度高、通用性强、可靠性好，适用于非等周期的采样点数据，不依赖于目标运动模型(匀速直线、变速直线、转向机动等模型)，能够获取采样点之外的位置和速度数据，支持单运动目标和多运动目标的参数测量。

1 基于最小二乘拟合的运动目标测速

无人机对运动目标测速，是通过采集无人机的侦察影像(如序列航空相片、侦察视频、视频序列静帧图像等)和遥测参数，基于无人机位置和姿态角、光电平台姿态角、运动目标的图像像素等数据，实现对运动目标的位置坐标、速度大小和方向、加速度等参数的解算。典型应用为：通过专用接口和采集模块采集无人机的遥测数据和侦察影像，快速解算和分析运动目标参数，并上传至指挥所和火力武器分队，进而实施对运动目标的打击。

1.1 基于成像模型的目标定位原理

无人机序列图像中存在运动目标，可利用无人机位置和姿态角、光电平台姿态角等遥测参数，基于成像模型的定位方法，计算出目标在不同序列图像中的位置坐标。基于成像模型的定位方法实时性好、易于实现，可解算出图像上任意点的坐标[6-7]。

图1所示为运动目标定位的示意图。定位过程中使用了像空间坐标系、无人机机体坐标系、无人机地理坐标系、平面直角坐标系等4个坐标系，各坐标系定义如下：

图1 运动目标定位示意图

1) 像空间坐标系OsXsYsZs(下文简称s系)。

原点Os为光学成像投影中心，相机光轴为OsYs轴；OsXs轴、OsZs轴分别平行于成像面阵外框且与图像显示存储方向一致。

2) 无人机机体坐标系ObXbYbZb(下文简称b系)。

坐标原点Ob为无人机质心，ObYb轴与机体纵轴重合，指向头部为正；ObZb轴在纵向对称面内，向上为上；ObXb轴垂直于ObYbZb平面，从后往前看向右为正；当光电云台偏转角为零，无人机机体坐标系与像空间坐标系三轴平行。

3) 无人机地理坐标系OeXeYeZe(下文简称e系)。

坐标原点Oe为无人机质心，OeXe轴指向正东，OeYe轴指向正北，OeZe轴垂直于OeXeYe平面，向上为正；当无人机姿态角为零，无人机地理坐标系与无人机机体坐标系三轴平行。

4) 平面直角坐标系OgXgYgZg(下文简称g系)。

平面直角坐标系与无人机地理坐标系三轴平行。

设航空相机或摄像机云台的高低角为α，方位角为β，设无人机的航向角为ψ，俯仰角为θ，倾斜角为γ。根据坐标变换原理，得到不同坐标系之间的坐标变换矩阵：

像空间坐标系s到无人机机体坐标系b的坐标变换矩阵表示为：

(1)

无人机机体坐标系b到无人机地理坐标系e的坐标变换矩阵表示为：

(2)

设目标在无人机地理坐标系e中的坐标为(xe，ye，ze)，目标在像空间坐标系s中的坐标为(xs，ys，-f)，f为相机或摄像机焦距。则两者之间的坐标变换关系表示为：

(3)

设目标在平面直角坐标系g中的坐标为(xg，yg)，无人机在平面直角坐标系g中的坐标为(xa，ya)，H为无人机与地面目标点的相对高度。则基于无人机姿态数据、航空相机或摄像机的姿态数据和内参数等遥测参数，根据成像模型可得：

(4)

结合式(3)和式(4)，可得出共线条件方程为：

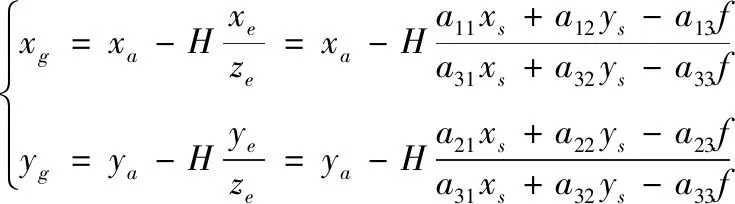
(5)

1.2 基于最小二乘多项式拟合的测速方法

基于成像模型的定位受测量误差影响较大，运动目标存在定位误差。由式(4)可知，序列图像中目标位置信息会受到无人机坐标(xA，yA)、无人机相对高度(H)、无人机姿态角(ψ，θ，γ)、云台姿态角(α，β)、成像焦距(f)等测量因素的影响，从而将导致定位数据在真实数据附近随机波动。对运动目标定位数据进行最小二乘多项式拟合，求得目标位置的平滑曲线多项式，能够一定程度上抑制系统噪声和测量误差等对目标定位和测速的影响。

最小二乘多项式拟合是一种数学上的近似和优化，利用已知数据拟合得到曲线多项式，使得已知数据和曲线的距离平方和最小[12-15]。基于最小二乘多项式拟合的目标测速，可应用于多种机动运动模式，适用于仅有少量采样数据、采样非等间隔等情况，能够推测解算出观测采样点之外时刻的速度值。

采用多项式拟合目标的运动轨迹，多项式表示为：

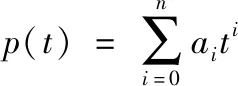
(6)

式(6)中：t为时间；p(t)为t时刻的拟合位置值；ai为系数；n为拟合多项式的阶数；m为采样点数。当n+1

将式(6)扩展成矩阵形式为：

P=CA

(7)

其中，pi为第i个采样点的位置，其为二维坐标(xi，yi)；ti为第i个采样点的时刻值。

基于最小二乘法，求解式(6)为：

A=(CΤC)-1CΤP

(8)

车辆、船艇、装甲集群等目标一般运动过程中机动性较小，因此位置坐标对时间的四阶导数或五阶导数，一般已趋近于零，拟合多项式的阶数n一般可取3或者4。此处若选择n=3，则位置、速度、加速度的拟合多项式可分别表示如下：

① 位置拟合多项式：p=a0+a1t+a2t2+a3t3。

② 速度拟合多项式：v=a1+a2t+a3t2。

③ 加速度拟合多项式：s=a2+a3t。

实际应用时，通常分别对位置坐标x、y进行拟合为：px=a0x+a1xt+a2xt2+a3xt3，py=a0y+a1yt+a2yt2+a3yt3；速度表示为：vx=a1x+a2xt+a3xt2，vy=a1y+a2yt+a3yt2。

无人机对地面运动目标测速，可假定地面为平面，主要关注目标质心在平面直角坐标系中的位置坐标，忽略目标的高程信息。设目标在tm时刻的位置为(xm，ym)，速度为(vmx，vmy)。如图2所示，速度vm和运动方向角ψm计算如下：

(9)

图2 运动目标速度示意图

2 实验测试

针对无人机对运动目标速度测量的应用需求，利用 VC++ 与QT开发环境，设计了无人机信息综合处理软件。该软件主要包括数据采集、图像预处理、图像拼接、目标检测识别、目标跟踪、目标定位等功能模块。运动目标测速为目标定位模块的重要功能，分别采用了均值法、卡尔曼滤波法和最小二乘拟合法，实现了运动目标测速功能。图3为无人机的一组序列航拍相片，以该组图像为例开展测试验证，对图3中方框标注的运动车辆进行速度测量。图4为基于最小二乘拟合的无人机运动目标测速结果图。分别采用了均值法、卡尔曼滤波法和最小二乘拟合法进行了运动目标测速测试。均值法测试结果为：目标速度大小22.4 m/s和方向159.8°，需要注意的是该方法主要针对匀速直线运动，应用于其他运动模式在理论上存在计算误差；对于卡尔曼滤波方法而言，由于测试样本数量少，滤波方法不能收敛，未能获得稳定的输出值。