风载荷作用下井基导弹冷发射动力学仿真

高 宇，周仕明，李道奎

(国防科技大学 空天科学学院， 长沙 410073)

与传统发射技术相比，井基冷发射技术反应快、精度高、威力大，是当今弹道导弹发射技术的研制重点[1]。垂直冷发射的导弹从出筒后至点火前处于完全失重状态，风载荷对其飞行姿态具有不可忽略的影响[2]。罗超等[3]通过数值模拟车载导弹的冷发射过程，研究了导轨滑块间隙和风速对导弹出筒姿态的影响；李显龙等[4]利用数值风洞技术，分析了平均风和脉动风作用下的车载导弹冷发射动力学响应；张筱等[5]建立了SS-18导弹冷发射系统的多体动力学模型，模拟各初始扰动对导弹出筒姿态的影响；岳玉娜等[6]以舰载导弹为研究对象，得到了海面风载荷作用下导弹出筒轨迹的变化曲线。

井基导弹具有较强的环境适应性和抗击打能力，常被用于执行恶劣环境下的作战任务[7]，但现有文献中对井下冷发射导弹受高速风载作用的系统研究尚为空白。本文针对某典型井基导弹问题，建立考虑风载荷对导弹作用的有限元仿真模型，模拟恶劣环境冷发射过程中风载荷对导弹的扰动，分析各级风力下导弹的动力学响应规律，研究结果对改善导弹出筒姿态、保证冷发射过程的安全性与可靠性具有一定的参考价值。

1 冷发射系统原理

某典型井基导弹冷发射系统结构简图如图1。

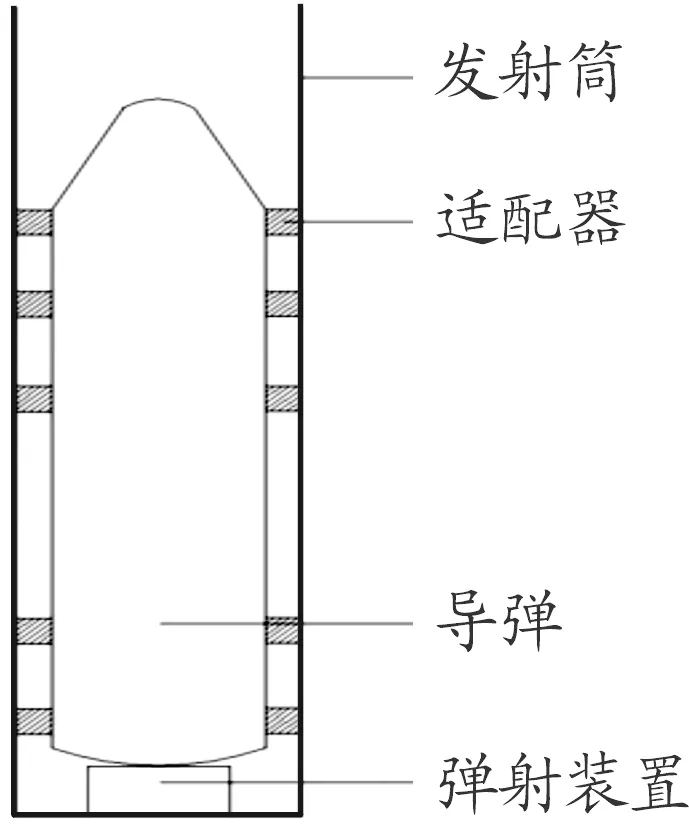
图1 导弹冷发射系统结构简图

冷发射系统包含发射筒、弹射装置、适配器和导弹4部分。发射筒垂直放置于发射井中，筒体与井壁之间设有支撑减振系统；弹射装置安装于发射筒底部，通过释放高压燃气-蒸汽混合气体产生推力[8]，作用于导弹尾罩将其弹射出筒；导弹与发射筒之间设置有多级适配器，通过锁紧装置固定在导弹表面，在导弹出筒过程中起支撑、导向和减振作用[9]，各级适配器出筒后依次与弹体脱离。导弹被弹射出筒一段距离后点火作程序飞行。

2 冷发射系统动力学建模

2.1 动力学原理

本文采用Newmark法[10]计算冷发射系统的动力学响应。弹体的动力学方程为

(1)

其中：M为导弹质量矩阵；C为导弹阻尼矩阵；K为导弹刚度矩阵；U为弹体位移；Rt为弹体所受外载荷矢量。

Newmark法假定在时间间隔[t，t+Δt]内加速度呈线性变化，即

(2)

(3)

式中α和δ为按积分的精度和稳定性要求可以调整的参数。将式(2)(3)代入式(1)中整理可得

(4)

(5)

(6)

2.2 风载荷简化

研究冷发射系统在恶劣工况下的动力学响应时，风载荷是主要考虑的一项外界激励因素。相比于车载和舰载冷发射导弹，井基导弹贮存环境好、反应速度快、抗打击能力强，更适用于执行恶劣环境下的发射任务，需要选取较高风级的载荷进行模拟。井基垂直发射导弹与车载、舰载导弹相比体量也更大，受风载作用面积和作用时长相应增加，动力学响应更加明显[12]，在建模时应当分段逐级对其加载，以更好得模拟大长细比导弹的出筒姿态。

在实际研究中，除了特殊地形要求外，一般忽略铅垂风对结构的影响，只考虑水平风载荷。根据风载荷作用周期的长短，又可以将水平风分解为周期较长、幅值稳定的平均风和周期较短、随机变化的脉动风[13]，如图2所示。

图2 风压时程曲线

工程中常用风压来表示风载荷的大小，任一高度处的风压为上述两类风的叠加，即

wz=wzs+wzd

(7)

其中，wz为总风压(Pa);wzs为平均风压(Pa);wzd为脉动风压(Pa)。

平均风压由于场地地貌、结构高度、结构体型不同而不同，表达为

wzs=μsμzw0

(8)

式中:μs为风载荷体型系数；μz为风压高度变化系数；w0为基本风压(Pa)。对于井下冷发射的导弹，在出筒后至点火前始终处于近地面高度，可以忽略高度对风压的影响，将平均风载荷简化为恒定值。

在脉动风的计算中，功率谱密度函数是衡量风载荷大小的一项重要指标，它反映了风载荷在频域上功率密度的大小。我国一般采用Davenport谱作为功率谱密度函数[14]，其表达式如下

(9)

式中，Sv(n)是脉动风速功率谱密度函数(m2/s)；v10是标准高度为10 m处的平均风速( m/s)；k是地面粗糙度系数；n是脉动风频率(Hz)；x常取1 200n/v10。

由式(9)易得，脉动风频率与功率谱密度函数成反比。不妨取v10为7级风最大风速17.1 m/s，地面粗糙系数k为0.005，时间步长0.01 Hz，借助MATLAB软件计算该工况下的脉动风功率谱密度函数曲线如图3所示。

图3 脉动风速功率谱密度函数曲线

由图3可知，脉动风的功率随频率增加呈指数衰减，在0～0.5 Hz频率范围内其功率相对较高，脉动风载荷对结构的影响较大。考虑到冷发射过程持续时间很短，脉动风对导弹出筒过程的影响主要依靠其低频部分，而这段时间内低频脉动风的变化很小，可以将其近似为恒定载荷。

通过上述两次简化，本文将平均风载荷与脉动风载荷都等效为静载荷，进一步可以通过空气阻力法进行计算，表达为

F=CρSv2/2

(10)

式中，C为空气阻力系数，与物体迎风外形有关，导弹可以看作是无数个圆柱体的叠加，该值取0.7；ρ为空气密度，取 1.293 kg/m3；S为结构迎风面的最大截面积(m2)；v是风与作用物体相对运动速度，对于本文所研究的对象可直接取风速( m/s)。

将导弹迎风面沿轴向长度划分为n段，分别计算各部段的迎风面积Si，按照出筒时间加载n组依次生效的集中力Fi，方向沿X轴正方向，模拟风载荷对导弹出筒过程的作用。

结合我国气候特点并查阅全国风压分布[15]可知，现有发射基地及适宜发射场地所处地区的基本风压主要分布在150～500 Pa，基本风压与风速之间的换算关系近似为w0=v2/1 600[16]，对应风速为21.9～28.3 m/s。因此选取蒲福风力等级表中7～10级风的最大风速计算风载荷，模拟恶劣环境对导弹发射过程的外界激励，如表1所示。

表1 蒲福风力等级

2.3 仿真模型

通过有限元仿真软件ABAQUS建立井下冷发射系统的动力学模型，如图4所示。相比于车载和舰载冷发射装置，井基冷发射系统的建模不必考虑载具各部件的刚柔耦合，在忽略土层柔性的前提下可以将发射井及井内隔振装置简化为约束。对冷发射系统仿真建模如下：1) 导弹发射方向为Y轴正方向，弹体使用梁单元建模，赋予各舱段不同的截面属性和分布质量，不考虑其自身局部变形的影响；

图4 井下冷发射系统仿真模型示意图

2) 弹射装置使用实体单元建模，视作刚体；

3) 适配器使用实体单元建模，材料选取硬质聚氨酯泡沫，视作各向同性的弹性体；

4) 发射筒使用壳单元建模，材料为Q345钢，视作各向同性的弹性体；

5) 忽略导弹质量偏心对冷发射过程的影响。

对于仿真模型的约束和加载设置如下：

1) 忽略地面的柔性影响，在发射筒底部施加固支约束；

2) 弹射装置与发射筒之间施加绑定约束，二者之间不发生相对运动；

3) 导弹垂直放置于发射筒中，头部距发射筒口1 m，尾部与弹射装置接触且无摩擦；

4) 适配器与发射筒之间设置接触，摩擦系数0.15；

5) 适配器与导弹之间设置耦合，并添加生死单元，使各级适配器在出筒后依次失效；

6) 在弹射装置上表面和导弹尾罩处施加如图5所示的内弹道压力，模拟燃气-蒸汽产生的推力；

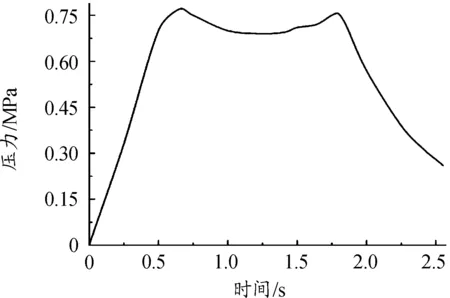
图5 内弹道压力曲线

7) 在弹体迎风面施加多组依次生效的水平载荷，模拟出筒过程中如图6所示风载荷的影响；

图6 风载荷示意图

8) 对模型整体施加重力场，方向竖直向下，大小为9.8 m/s2。

在完成上述建模设置的基础上，采用隐式动力学方法求解仿真模型，分别计算系统在无风、7级风、8级风、9级风、10级风下的动力学响应，对比弹体在各工况下的横向偏移大小、偏航角度变化、适配器受力情况，评估风载荷对井下冷发射系统的影响。

3 仿真结果及分析

3.1 仿真结果

首先模拟井下冷发射系统在不加风载荷时的动力学响应，输出导弹在发射过程中的位移、速度、加速度曲线如图7所示。由图7可知，在加载0.71 s后导弹开始出筒，在2.55 s时弹尾完全出筒，与此同时速度达到最大值，随后在重力作用下进行匀减速运动，于5.56 s时刻速度降为0，导弹达到最大偏移。以此无风工况为理想工况，将各级风力作用下的动力学响应与之对比，分析风载荷对导弹出筒的影响。

图7 无风载作用下导弹动力学响应曲线

1) 横向偏移

选取导弹弹头节点，输出其X方向的位移-时间曲线如图8所示，可以得到在各级风力作用下导弹出筒过程中的横向偏移。由图可知，在无风工况下弹体不发生横向偏移，随着风力等级的提升，弹体沿顺风方的位移也逐渐增大。导弹在出筒过程(0.71～2.55 s)中由于发射筒和适配器的约束，没有产生较大偏移，在完全出筒后失去了横向约束，水平位移迅速增大，在5.56 s时7～10级风作用产生的X方向位移对应为1.168 m、1.713 m、2.376 m、3.211 m。

图8 各级风载作用下导弹横向偏移曲线

2) 偏航角度

选取导弹弹头及弹尾节点，输出二者在X方向的位移，从而可得导弹发射过程中的偏航角κ。各级风载作用下导弹偏航角度如图9所示。如图所示，导弹在无风时偏航角度为0，风速越快偏航角度越大。导弹在完全出筒前由于弹尾不发生横向偏移，弹体产生的偏航角度很小；完全出筒后受风载荷激励产生较大偏航，在7～10级风作用下，导弹达到最高点处的偏航角分别是1.6°、2.4°、3.3°、4.4°。

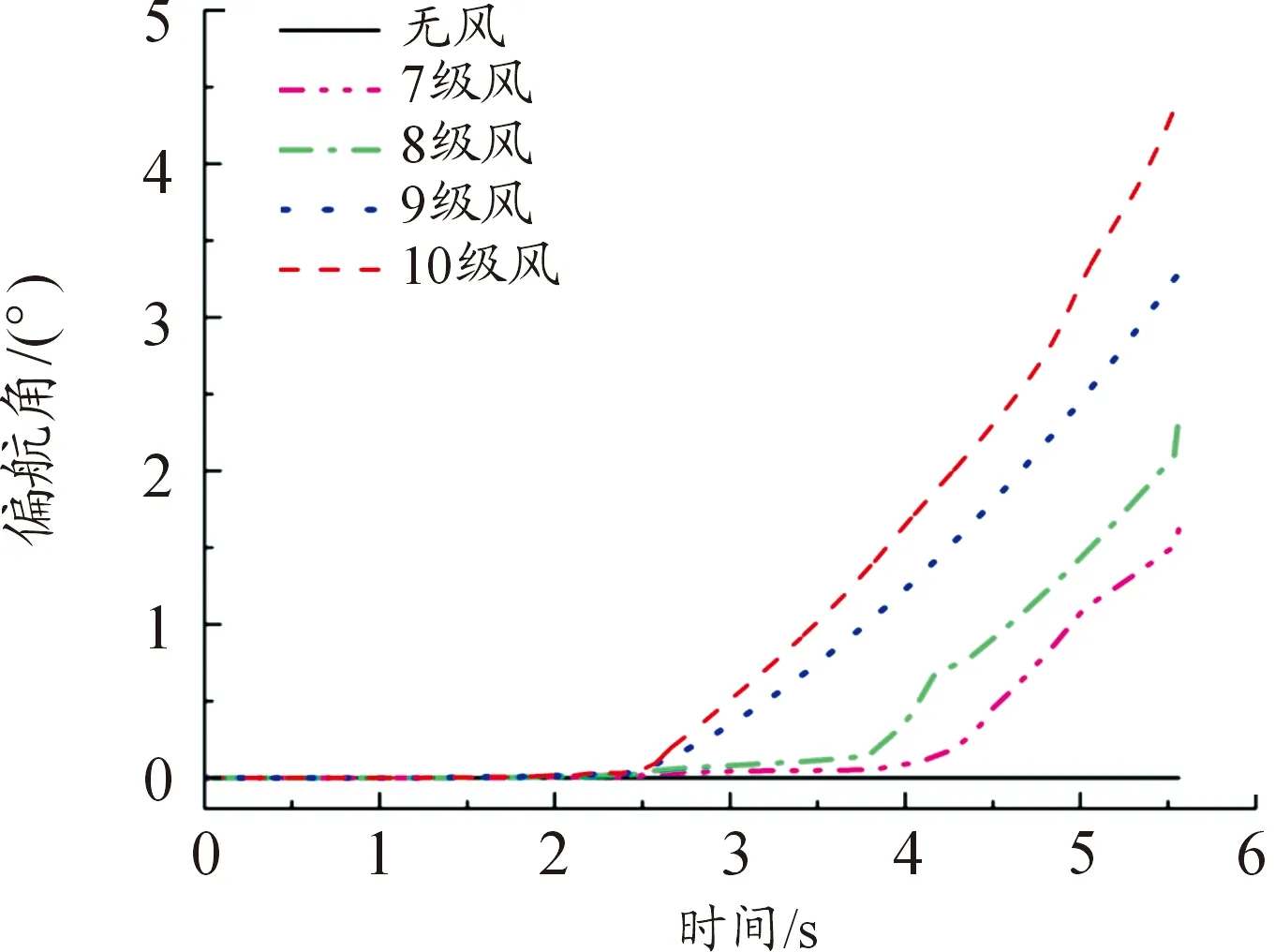
图9 各级风载作用下导弹偏航角度曲线

3) 适配器受力

在导弹冷发射过程中，适配器为其提供了横向约束，限制了弹体因自身变形和外界激励产生的变形。在各级适配器上分别选取相关单元节点，输出其法向接触力N如图10、图11所示。从弹头到弹尾分布的一至五级适配器，依次作为主要受力构件产生了五处接触力波峰，从图10(a)可以看出，无风情况下由于弹体自身变形产生了法向接触力，该幅值很小，本文不考虑其影响。7～10级风载作用下，各级适配器的受力规律一致：第一、二级适配器受力很小，第四、五级适配器受力较大。10级风载作用下各级适配器受力如图10(b)所示，第一、二级适配器因距弹头较近，在其出筒时导弹还未发生足够大的横向位移，所以受力不明显；随着弹体出筒长度的增加，所受风载荷逐渐增大，适配器受力情况也愈加显著，接近弹尾的第四、第五级适配器产生较大的接触力。对比图11(a)～(e)可知，接触力峰值出现在第四级适配器上，7～10级风使适配器产生的最大接触力依次为4 452 N、6 489 N、8 970 N、12 141 N。

图10 风载作用下各级适配器受力曲线

图11 各级风载作用下适配器受力曲线

4) 适配器布置

由适配器受力情况可知，适配器的受力与其所在位置有关。在上述仿真模型中，适配器采用的是如图12(a)所示的非均布布置方案，不妨建立适配器均布模型如图11(b)所示，输出二者在7级风作用下出筒过程(0～2.55 s)的动力学响应，对比分析适配器布置对冷发射系统的影响。

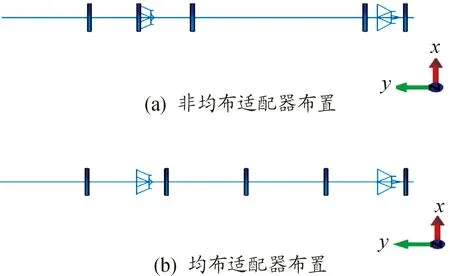
图12 适配器布置示意图

如图13、图14所示，导弹在出筒过程前期受各级适配器约束较大，没有产生明显的偏移或偏航，两种布置方案的动力学响应基本一致；在出筒过程后期，均布方案的第四级适配器相对靠近弹头，率先发挥约束作用，此时均布方案产生的偏移和偏航量较小；随着导弹继续升空，均布方案只剩下最后一级约束，而非均布方案的四、五级适配器同时发挥功效，此时非均布方案下的导弹出筒姿态更优。在导弹完全出筒时，采用非均布适配器会产生0.023 m的偏移和0.04°的偏航；采用均布适配器则产生0.027 m的偏移和0.05°的偏航。

图13 不同适配器布置下导弹横向偏移曲线

图14 不同适配器布置下导弹偏航角度曲线

输出两种布置方案下的各级适配器受力。由图15可知，前三级适配器在两种方案下的受力情况基本一致，后两级适配器在非均布方案下的受力明显大于均布方案。响应峰值出现在第四级适配器上，非均布方案下为4 452 N，均布方案下为2 011 N。

图15 不同布置方案下适配器受力曲线

3.2 分析讨论

将上述仿真结果整理如表2、表3所示。

表2 各级风载作用下系统动力学响应参数

表3 不同适配器布置下系统动力学响应参数

该模型的计算结果表明，风载荷对井基导弹冷发射过程有明显影响：

1) 在风载荷作用下，导弹出筒过程中对适配器造成了明显的挤压，使其产生了较大的接触力，在10级风作用下的最大接触力为12 141 N，可使适配器截面产生0.056 MPa的应力，此时系统仍能安全工作；

2) 弹体在出筒后、点火前沿顺风向产生明显的位移，相比于导弹全长，在7、8级风作用下导弹偏移小于5%，可以正常执行发射任务，在9、10级风作用导弹偏移大于5%，导弹出筒姿态较差，无法满足系统安全需求；

3) 风载荷对导弹偏航的影响相对较弱，在10级风作用下产生的偏航角度为4.4°，依然满足发射精度要求；

4) 随着风力等级的提高，风载荷对冷发射系统的影响愈发明显，风力从7级增大到8级，系统动力学响应幅值增长约50%，9级风响应超过7级风响应的2倍，10级风则近乎3倍，该规律可为工程设计提供参考；

5) 各级适配器对导弹的约束作用有明显差异，采用均布的适配器能有效减小适配器受力，采用非均布方案则对导弹出筒姿态有一定改善，工程实践中可以通过调整各级适配器的位置和强度，在满足发射精度需求的同时保证系统的安全稳定。

4 结论

1) 基于Newmark算法在有限元分析软件ABAQUS中建立了井基导弹冷发射系统模型，通过空气阻力法模拟风载荷，得到了各级风力作用下导弹出筒过程的动力学参数，对工程实践具有参考价值。

2) 风载荷对井基导弹冷发射过程产生了不可忽略的影响，系统响应幅值与风力等级成正比，主要表现为导弹沿顺风向产生偏移、偏航以及适配器受力变形。

3) 风载荷对导弹冷发射出筒过程的影响不可忽略，在实际操作中应尽量避免在大风天气发射，但在9级风力以下的风载作用时，井基冷发射系统仍具有执行发射任务的能力。

4) 可通过合理规划适配器排布、调整各级适配器强度等方法改善导弹出筒姿态，提高井基导弹冷发射系统的经济性、安全性和稳定性。