基于双十字形测量结构的磁信标定位方法*

赵 震杨宾峰王 润管 桦

(空军工程大学信息与导航学院，陕西 西安710000)

磁是自然界最普遍的现象之一，早在战国时期，人们就开始使用司南确定方位，随着人类对磁场的深入探索，磁技术被广泛应用到医疗、探矿、船舶和飞行器定位等领域[1-6]。 与无线电定位技术相比较，磁定位技术抗干扰性更好，对于遮挡物的穿透力更强。

在磁定位技术中，基于磁梯度张量(Magnetic Gradient Tensor，MGT)的定位技术，算法简单，精度高，成为磁定位技术研究的热点。 张朝阳等[7]利用磁偶极子模型推导出了MGT 定位算法公式，并进行了仿真分析。 李青竹等[8-9]对多种MGT 测量结构进行了比较，证明十字形结构具有最小的定位误差。王润等[10-11]提出了旋转磁信标MGT 的计算方法，可有效分离噪声信号。

在磁信标定位过程中，地磁场对信标磁场影响较大，随着运动载体与磁信标距离增大，定位误差随之变大。 在降低地磁场影响方面，于振涛等[12]对单点MGT 定位算法进行偏微分求导，提出了一种改进算法，该算法计算过程较为复杂，对磁传感器精度要求较高。 邓国庆等[13]通过预先测量地磁场强度，利用差分的方法消除地磁场，带来人为因素影响。 针对这些问题，基于双十字形测量结构的磁信标定位方法从单点MGT 算法出发，设计了一套有效降低地磁场干扰的定位系统。

1 磁梯度张量定位原理

1.1 磁梯度张量

在空间直角坐标系中，磁感应强度用三维列向量B(Bx，By，Bz)表示，Bx，By，Bz为磁感应强度在x轴、y轴和z轴上的分量。MGT为磁感应强度三个分量分别在x轴、y轴和z轴上的变化率，共有9 个元素，用三阶矩阵G表示:

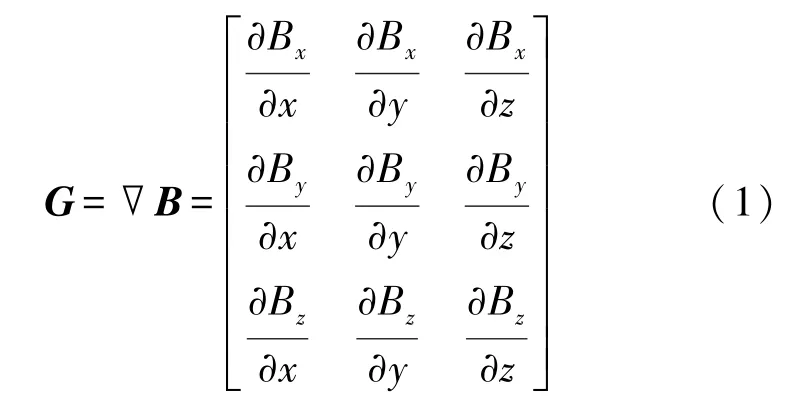
在磁信标定位系统中，一般使用永磁体作为磁信标，也可使用直流通电螺线管，此时磁信标空间磁场为静态磁场，由麦克斯韦方程组可知，磁感应强度的散度和旋度均为0，可求得G关于主对角线对称，且主对角线元素和为0，于是我们只需5 个独立的元素，便可确定任意空间点上的MGT。

1.2 磁梯度张量定位算法

磁信标尺寸远小于定位目标与磁信标之间的距离时，可将磁信标作为磁偶极子看待，并通过式(1)计算出空间任意点的MGT。 根据毕奥萨伐尔定理，与磁偶极子相对位置为r处点的磁感应强度为:

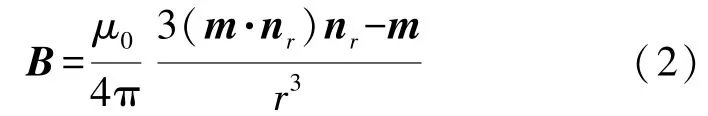
式中:μ0为真空磁导率，m为信标磁矩，nr为位置矢量r的单位矢量，r为矢量r的模。

假设r＋dr处的磁感应强度为B′，则两点间的磁感应强度差为:

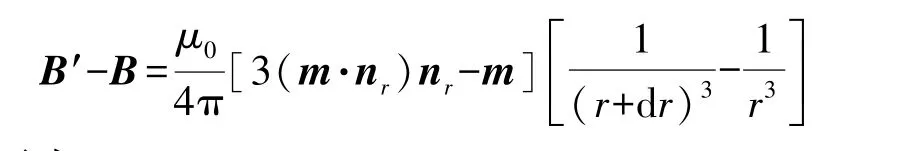
又因为

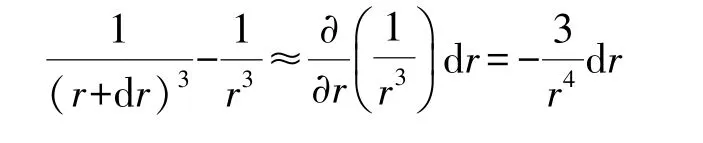
可得:

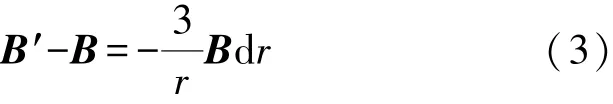
两点间MGT 还可表示为:

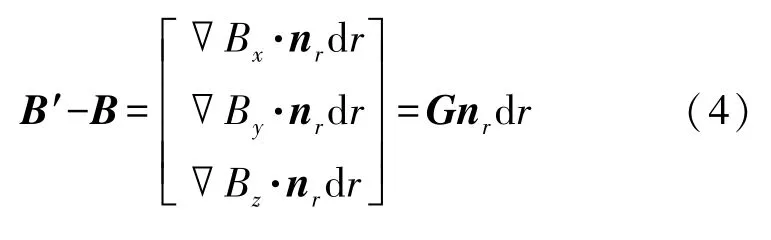
联立式(3)、式(4)，得出MGT 定位方程:

1.3 两点磁梯度张量定位算法

针对MGT 定位算法很难直接降低地磁场影响这一问题，提出了一种改进算法，通过测量相邻两点MGT，并利用磁矩与磁感应强度相关公式，推导出不依赖目标点磁感应强度的定位算法。 磁感应强度与信标磁矩的转化公式为:

m为信标磁矩，A是一个与目标位置相关的矩阵，其表达式为:

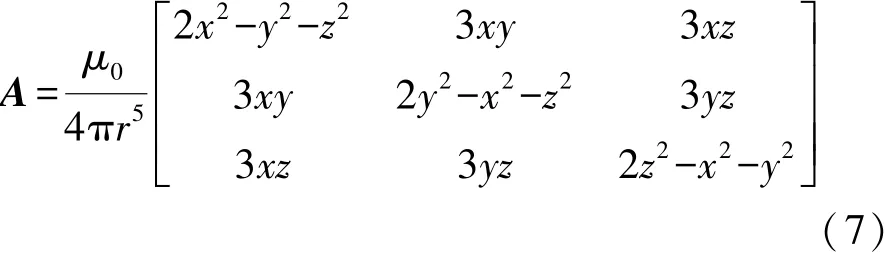
式中:(x，y，z)是目标位置坐标，r为目标到磁信标的距离。 设空间上两点坐标为:

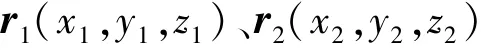
对应的磁梯度张量为G1、G2，依据式(5)、式(6)可得:

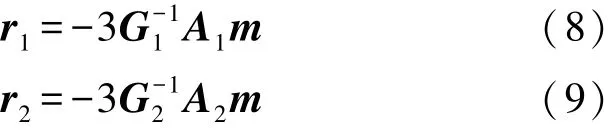
设两点间的距离矢量c＝r1-r2。 联立式(8)、式(9)，消去磁矩m，可得:

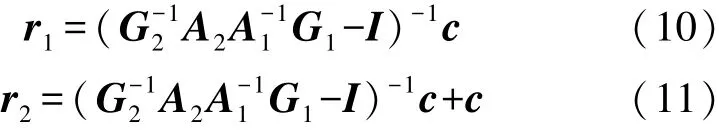
I是单位阵，G1、G2可通过磁测量结构计算得出，两点间的位置矢量c是预先设置的已知量，A1、A2只与r1有关，因此式(10)、式(11)是关于r1的非线性方程，通过设置目标函数，利用优化算法，能够求解出空间点的位置。

2 求解算法

较为常见的优化算法有最小二乘法、粒子群算法、萤火虫算法、免疫算法、差分优化算法等等。其中粒子群算法(Particle Swarm Optimization，PSO)是一种生物模拟优化算法[14-16]，算法中的每一个解都是一个“粒子”，这些“粒子”对于被优化的函数都有一个适应值，通过不断迭代，完成设定的迭代次数或者达到要求的适应值，从而搜索出最优“粒子”。 相较于其他优化算法，PSO 算法收敛速度快、容易实现、全局搜索性能好，本文使用粒子群算法求解。

根据式(10)，可设δ:

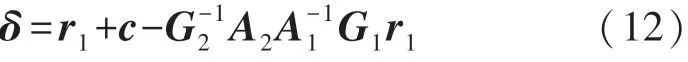
δ表示r1通过粒子群算法得到的解与其真实值的偏差，δ的模越小解越接近r1的真实值，因此可以用δT·δ衡量解的准确性。

设定目标函数f:

经过100 次迭代后，目标函数误差达到10-11数量级，能够保证系统具有较小的误差。

3 双十字形测量结构设计

MGT 定位系统的测量结构主要有三角形、十字形和正方形，对于测量误差而言，十字形优于正方形和三角形[17]。 考虑到需要计算两点的MGT，同时在系统定位过程中能够得出较准确的定位数据，较少出现定位误差突变，保持系统稳定性，在十字形测量结构的基础上构造出双十字形测量结构。 测量结构由水平、垂直两个平面十字形测量结构组合而成，如图1，共包含8 个三轴磁传感器，相邻两个传感器距离d均相等，传感器坐标轴对应平行。

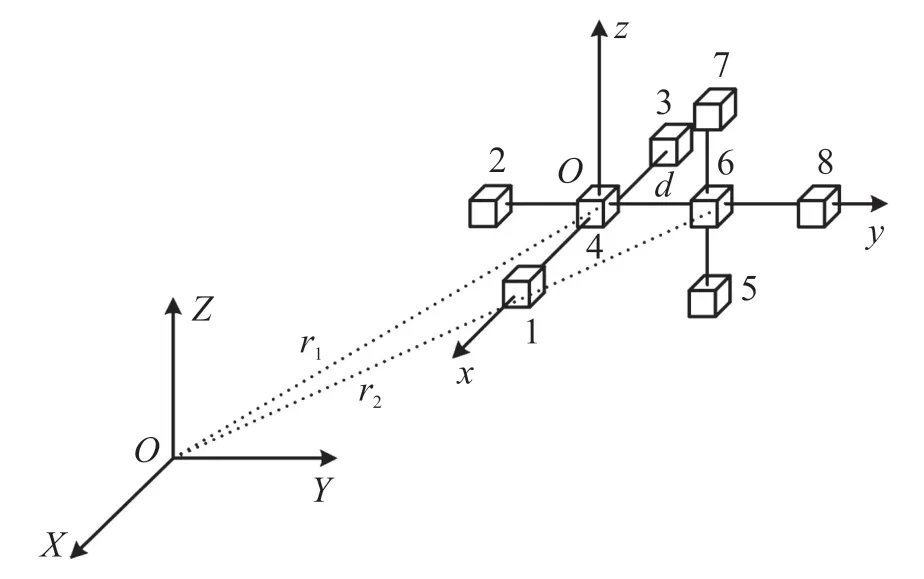
图1 双十字形测量结构示意图

以磁信标为原点构建空间直角坐标系，图1 展示了测量结构的内部关系，以及磁信标与测量结构的空间关系，测量结构被封装在一个长方体空间中，作为定位装置的一部分被安装在运动载体上。

用Bij(i＝1，2，…，8，j＝x，y，z)表示传感器i在j方向上的磁感应强度分量，其中矩阵Gi(i＝1，2)为对称阵，分别表示传感器4 和传感器6 所在点上的MGT 值，表达式为:

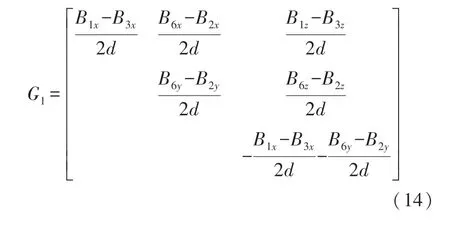
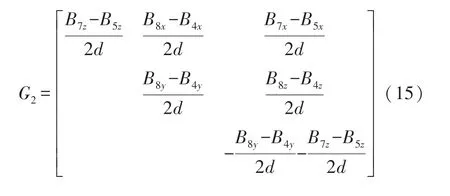
4 仿真实验

磁定位技术可应用于钻井、小型无人机起降、潜艇下潜和上浮等场景，在这些领域内，更关心竖直方向上的定位精度，因此设定运动载体沿竖直方向运动。 同时，两点MGT 定位方法是通过空间点的磁场信息与其位置信息建立对应关系，从而确定空间点的位置坐标，误差不随时间积累，在优化算法计算速度较快的情况下，不需引入位置与速度的约束关系就可实现实时定位。

仿真实验条件:建立以磁信标为原点的空间直角坐标系，信标磁矩m＝(5×107A·m2，0，0)，传感器间距设置为0.1 m、精度0.01 nT，粒子群算法最大迭代次数为100 次。 运动载体由点(20 m，20 m，2 m)沿直线运动至点(20 m，20 m，50 m)。 分别验证磁矩、传感器精度、传感器间距，以及引入随机噪声和恒定磁场后，基于双十字形测量结构的磁信标定位方法误差变化。

4.1 传感器精度对定位误差影响

随着传感器技术的发展，体积更小、精度更高的磁传感器逐渐出现，磁传感器应用领域更加广泛。为了达到实验目的，分析传感器精度对定位影响，设置传感器精度分别为1 nT、0.1 nT 和0.01 nT，信标磁矩为(5×107A·m2，0，0)，传感器间距0.05 m，进行仿真实验，误差变化如图2 所示。

从图2 可以看出，传感器精度为1 nT 的定位误差最大，z 轴50 m 内最大定位误差为67 m，传感器精度提升后，定位误差显著降低，精度为0.01 nT 的最大误差仅为1.56 m，且96%的定位误差在1 m 以内，可以看出传感器精度对定位误差影响很大。 对传感器而言，精度越高、体积越小，价格就越高，制造工艺也会更加复杂，在选取传感器时，必须综合考量精度、稳定性、价格等要素。

4.2 传感器间距对定位误差的影响

考虑到计算MGT 时，必须用到传感器间距d，同时对于运动载体而言，测量结构不能过大，设置传感器间距分别为0.05 m、0.1 m 和0.2 m，传感器精度为0.01 nT，信标磁矩为(5×107A·m2，0，0)，计算不同传感器间距的定位误差，结果如图3 所示。

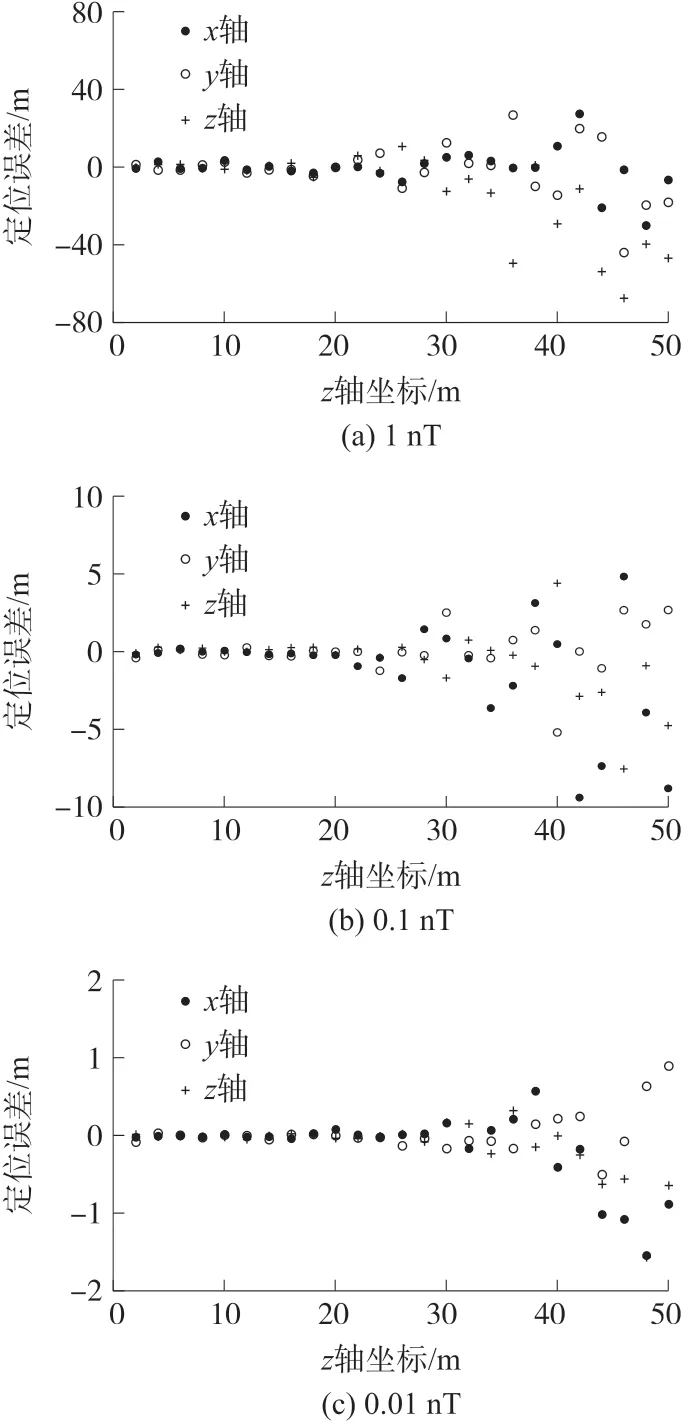
图2 传感器精度对定位误差影响

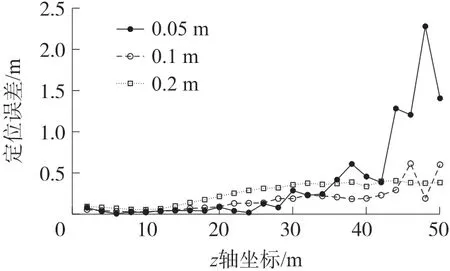
图3 传感器间距对定位误差影响

图3 中三条误差变化曲线相差不大，仅在z轴35 m 以后传感器间距为0.05 m 的误差变化较为明显，同时传感器间距与定位误差不存在比例关系，但是可以选择合适的传感器间距，确保定位误差符合要求，同时具有较好的平稳性。

4.3 磁矩大小对定位误差的影响

对于磁信标而言，磁矩会影响磁感应强度，磁矩越大，空间点上的磁感应强度也越大，同时磁信标的体积和成本也会增加，这里设置磁矩分别为(0.5×107A·m2，0，0)、(1.5×107A·m2，0，0)、(5×107A·m2，0，0)，传感器间距为0.1 m，精度为0.01 nT，进行仿真实验，图4 表示不同磁矩的定位误差变化。

对比图4 中的三条误差曲线，磁矩为(0.5×107A·m2，0，0)时，误差变化范围从0.06 m 到3.62 m，相较于其他磁矩，误差较大。 整体上看，信标磁矩越大，误差越小、变化越平稳。z轴25 m 内，三条误差曲线最大相差0.2 m，25 m 至50 m 时，误差最大相差3 m，提高磁矩具有降低定位误差的作用，但提升信标磁矩的同时也会增加成本，在定位距离较近的情况下(25 m 以内)，可以选取磁矩较小的磁信标，不仅能够确保较小的定位误差，还能降低系统成本。

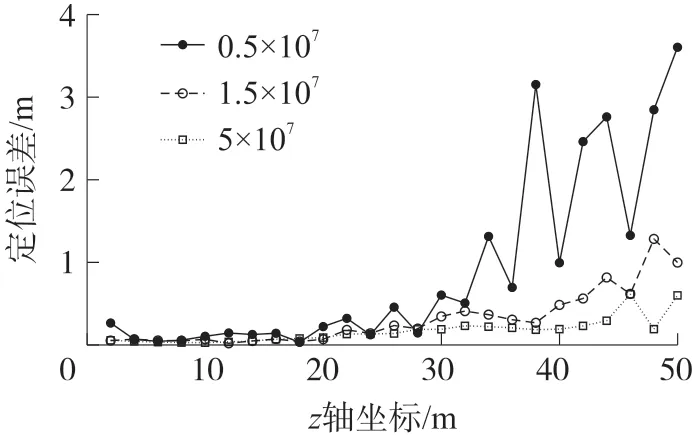
图4 磁矩对定位误差影响

4.4 随机噪声对定位误差的影响

在空间环境中存在着自然和人为的随机磁噪声信号，噪声会影响传感器对磁感应强度的测量，产生定位误差。 设置信噪比分别为70 dB、80 dB、90 dB的磁信号，进行定位误差对比，结果如图5 所示。

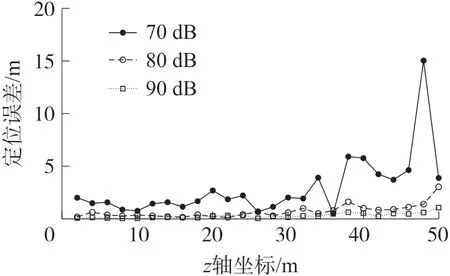
图5 信噪比对定位误差影响

从图5 可以看出，信噪比为80 dB 和90 dB 时，定位误差较小，环境中的随机噪声对定位影响不大，z轴50 m 内最大误差分别为3 m 和1 m。 70 dB 信噪比时，噪声持续对定位系统产生较大影响，相对定位误差达到100%以上，绝对误差最大达到15 m，严重影响定位可靠性。 从整体上看，信噪比越大，定位误差越小，在较强随机噪声(信噪比小于70 dB)影响下，系统定位可靠性变差。

4.5 恒定噪声条件下两种定位方法误差比较

地球表面附近存在着地磁场和各种异常磁场，这些磁场影响范围大，变化连续、平稳，在较小范围内，可认为地磁场恒定不变。 对于磁矩较小的磁信标，不能忽视恒定磁场引起的定位误差，于是在信标磁场中引入强度为(0，0，1 000 nT)的恒定磁场，计算十字形测量结构MGT 定位方法和双十字形测量结构两点MGT 定位方法的误差，结果如图6 所示。

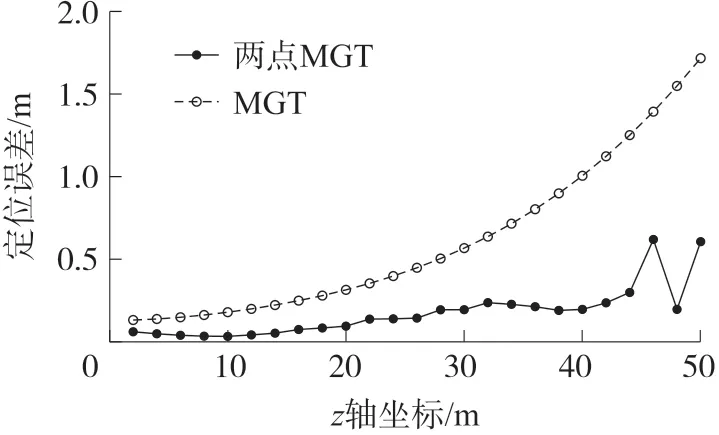
图6 MGT 和两点MGT 定位误差对比

图6 表明，在z轴方向加入1 000 nT 的恒定磁场后，MGT 定位误差随定位距离增大而缓慢增长，最大误差为1.72 m，大于两点MGT 的0.62 m。 可以看出，在地磁场和其他恒定磁场的影响下，基于双十字形测量结构的定位方法可有效减小定位误差，其结果优于十字形测量结构MGT 定位方法。

5 总结

本文提出了一种利用两点MGT 进行定位的方法，设计出了计算两点MGT 的双十字形测量结构，并通过粒子群优化算法求解出了目标位置。 仿真结果表明，z 轴25 m 外，磁传感器精度和信标磁矩是影响定位误差的主要内部因素，整体上看，传感器精度越高、信标磁矩越大，定位误差越小；不能忽略随机噪声对定位误差的影响，信噪比低于80 dB 时，定位误差显著增大，系统可靠性降低；地磁场和其他恒定噪声会对信标磁场产生影响，此时，基于双十字形测量结构的两点MGT 定位方法显现出其优越性，其结果优于十字形测量结构MGT 定位方法，同时相较于其他消除地磁场影响的方法，本文方法实现简单，定位精度高，不存在人为因素影响。