园林植物害虫桂花网蝽的空间分布特征
2021-04-08刘平晏青华文仕军阮桢媛胡建银龚静林
刘平,晏青华,文仕军,阮桢媛,胡建银,龚静林
(1.云南林业职业技术学院,云南昆明 650224;2.西南林业大学,云南昆明 650224;3.江西省贵溪中心苗圃,江西贵溪 335400)
桂花Osmanthus fragrans属于重要的园林绿化树种,大量栽种于昆明的各大公园、小区及道路两侧。近几年,桂花叶上发现大量的桂花网蝽危害,该虫以若虫及成虫于桂花叶背面刺吸植物汁液造成危害,使叶片褪绿,其排泄物诱发煤污病,严重影响植物叶片的光合作用,导致受害植株树势衰弱、萌发能力降低、开花数量减少,极大影响桂花树的生长及观赏价值。
桂花网蝽Eteoneus sigillatusDrake et Poor,又叫星菱背网蝽,隶属半翅目Hemiptera网蝽科Tingidae菱背网蝽属[1-2],在云南、贵州均有分布[3]。目前,国内对桂花网蝽的报道较少,扈克明 等在云南西双版纳原生林进行昆虫调查时首次发现有E.sigillatus,当时该虫的寄主还不能明确[4]。之后,李传仁对中国网蝽科进行系统研究,将采自云南昆明、安宁等地的E.sigillatus寄主确认为桂花[3]。贵州省林业科学研究院的吴跃开对桂花网蝽的形态特征及生物学习性进行了研究,并提出一些防治建议[5]。2019年笔者对昆明市桂花上的桂花网蝽的空间分布型进行了调查,在此基础上确定了最适抽样数和序贯抽样表,以期为获取准确、系统的虫情调查资料提供依据。
1 研究方法
1.1 研究区概况 研究区位于云贵高原中部的云南省昆明市主城区。 昆明市(24°23′~26°22′N,102°10′~103°40′E)地势北高南低,平均海拔 1 895 ~1 990 m,属北纬低纬度亚热带-高原山地季风气候,由于受印度洋西南暖湿气流的影响,日照长、霜期短,年平均气温15℃,年均日照2 200 h左右,无霜期240 d以上,年降水量1 450 mm。调查地点为昆明金殿公园、黑龙潭公园、云南农业大学校园、圆通山公园、月牙潭公园、金林碧水小区、清水河一带等桂花树较多的公园、小区、道路边行道树及绿化带(表1)。

表1 调查样地概况Tab.1 The overview of the sample plots
1.2 调查方法 2019年7月中旬,对7块样地桂花树上桂花网蝽的虫口数量进行调查。每个调查地设1个样地,面积0.1 hm2。每个样地均匀地抽查30株桂花树,每株桂花树按东西南北4个方位,每个方位分上中下3个位置共选取12个位点,每个位点取1段15 cm桂花梢头详细调查网蝽数量,记录桂花网蝽的成虫数量,计算虫口密度。
1.3 数据分析方法
1.3.1 聚集度指标法 依据调查数据,计算每块样地桂花网蝽成虫的平均虫口密度m、样本方差s2。
扩散系数C=s2/m。当C=1时,为随机分布;C>1时,为聚集分布;C<1时,为均匀分布[6]。
Cassie指标CA=(s2/m-1)/m。当CA=0时,为随机分布;CA>0时,为聚集分布;CA<0时,为均匀分布[7]。
聚集性指标m*/m=1+(s2-m)/m2(平均拥挤度m*=m+s2/m-1)。当m*/m=1时为随机分布;m*/m>1时,为聚类分布;m*/m<1时,则为均匀分布[8]。
丛生指标I=s2/m-1。当I>0时,为聚集分布;I=0时,为随机分布;I<0时,为均匀分布[9]。
负二项分布k值,k=m2/(s2-m),k值越小,聚集度越大。k值趋于∞时(一般在8以上)逼近泊松分布;8 >k>0,为聚集分布;k<0,为均匀分布[10]。
1.3.2 回归分析法 利用样本平均数m和方差s2的对数值计算Taylor幂法则回归模型[11],lgs2=lg a+b lgm。a、b为引入的参数。 当 lg a=0,b=1时,种群为随机分布;当lg a>0,b=1时,种群为聚集分布,此时b值恒定,分布不具密度依赖性;当lg a>0,b>1时,种群为聚集分布,分布具有密度依赖性;当lg a<0,b=1时,种群为均匀分布,且密度越高,分布越均匀。
Iwao的回归模型[12]m*=α+βm。当α=0、β=1时,种群分布型为随机型,分布的基本成分为单个个体;当α>0、β=1时,种群为聚集分布,个体间相互吸引,分布的基本成分为个体群,个体群为随机分布;当α=0、β>1时,为具有公共k值的负二项分布;当α>0、β>1时,为个体群的聚集分布;当α=0、β<1或0>α>-1、β=1时为均匀分布。
1.3.3 空间分布型频次分布检验 将调查数据列成频次分布表,利用其进行频次分布检验,获得二项分布、泊松分布、负二项分布、泊松-二项分布、奈曼分布、Weibull分布的理论频次,确定桂花网蝽所属分布型。
1.3.4 最适抽样数的确定 在实际抽样调查中,既要保证工作效率又要确保抽样具有代表性和精准性。依据Iwao[13]的方法,只要昆虫种群数m*与m成线性关系,就可以利用聚集度参数α、β来计算在给定允许误差(D)及密度下的最适理论抽样数。
1.3.5 序贯抽样模式 利用 Iwao提出的序贯抽样模式,计算桂花网蝽成虫序贯抽样数。


式中,T1(0)、T0(n)为序贯抽样累计虫量的上、下限,n为抽样株数,m0为判别密度(即防治指标),t为置信度。
2 结果与分析
2.1 聚集度指标测定 桂花网蝽的聚集度指标如表2所示,5种聚集度指标测定的7组数据中,C>1;CA>0;m*/m>1;I>0,8 >k>0,依据聚集度指标的判定标准,桂花网蝽成虫在桂花上的空间分布型为聚集分布。

表2 桂花网蝽成虫聚集度指标Tab.2 Aggregation indices of E.sigillatus adult
2.2 线性回归方程检验
1)Taor幂法则的lgs2与lgm回归方程lgs2=0.369 11+1.273 98 lgm,相关系数r=0.789 4。方程中,lg a>0,b>1,说明桂花网蝽呈聚集分布型,分布具有密度依赖性。
2)Iwao的m*与m回归模型m*=2.675 03+1.089 71m,相关系数R=0.934 3。方程中,α>0、β>1,说明桂花网蝽呈聚集分布型。
2.3 空间分布型频次分布检验 根据调查数据的频次测定拟合结果得出7种分布的频次测定拟合图(图 1,2,3,4,5,6,7)。 可以看出,负二项两种分布拟合效果最好且其卡方值分别为300.528 0,244.329 1(表3)。说明桂花网蝽的空间型属于聚集分布中的负二项分布。

表3 7种分布型频次测定卡方值Tab.3 Chi-square value of 7 distribution frequency measurement

图1 二项分布频次测定拟合图Fig.1 Binomial distribution frequency determination fitting figure
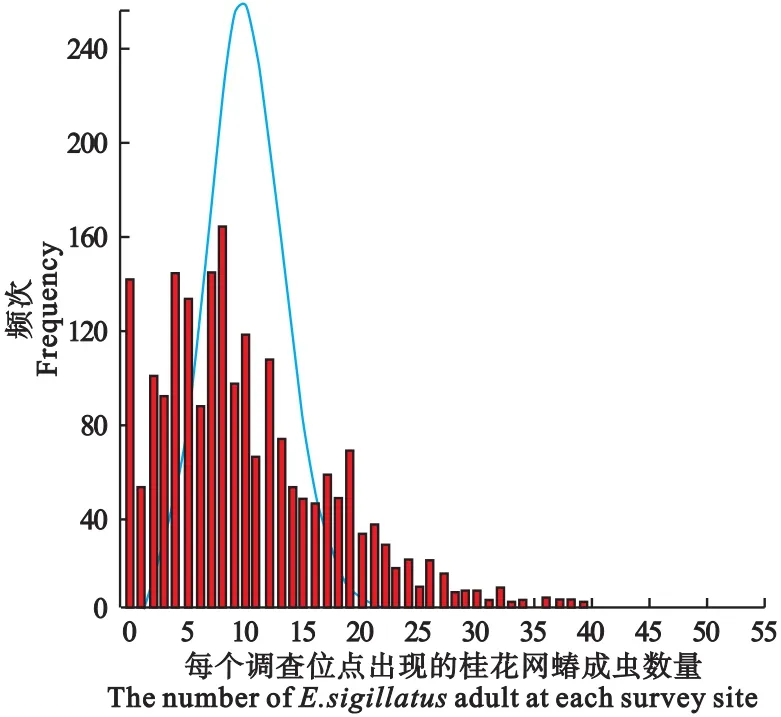
图2 泊松分布频次测定拟合图Fig.2 Poisson distribution frequency determination fitting figure

图3 负二项分布(矩法)频次测定拟合图Fig.3 Negative binomial distribution(moment method)frequency determination fitting figure

图4 负二项分布(似然法)频次测定拟合图Fig.4 Negative binomial distribution(maximum likelihood method)frequency determination fitting figure

图5 泊松-二项分布频次测定拟合图Fig.5 Poisson-binomial distribution frequency determination fitting figure

图6 奈曼分布频次测定拟合图Fig.6 Neyman distribution frequency determination fitting figure

图7 Weibull分布频次测定拟合图Fig.7 Weibull distribution frequency determination fitting figure
2.4 最适抽样数的确定 按Iwao的m*-m回归方程确定理论抽样数(N)公式。

式中α、β为Iwao模型参数,α为2.675 03,β为1.089 71,t为一定概率保证下的正态离差值,田间调查一般取1;D为允许误差,取0.1或0.2;m为平均虫口密度。当D=0.1时最适抽样公式为N=367.503/m+8.971,当D=0.2时最适抽样公式为N=66.875 75/m+2.242 75,桂花网蝽成虫理论抽数见表4。
由表4可知,桂花网蝽的调查理论抽样数与虫口密度和允许误差有关,虫口密度一定时,允许误差越大,理论抽样数越少;允许误差一定时,虫口密度越大,理论抽样数越少。

表4 桂花网蝽成虫理论抽样数 单位:株Tab.4 Theoretical sampling number of E.sigillatus adult Unit:plant
2.5 序贯抽样 将α=2.675 03,β=1.089 71代入T1(0)、T0(n),置信度t取 90%即t=1.65,m0为判别虫口密度(防治指标),因桂花网蝽尚无防治经验,故分别拟定为10头/株、5头/株,分别计算出序贯抽样数值(表5)。由表5可知,例如调查25株时,防治指标为5头/株,累计虫数超过162头时须进行防治,累计虫数少于88头则不需防治,累计虫数在上限和下限之间,应继续增加抽样数。
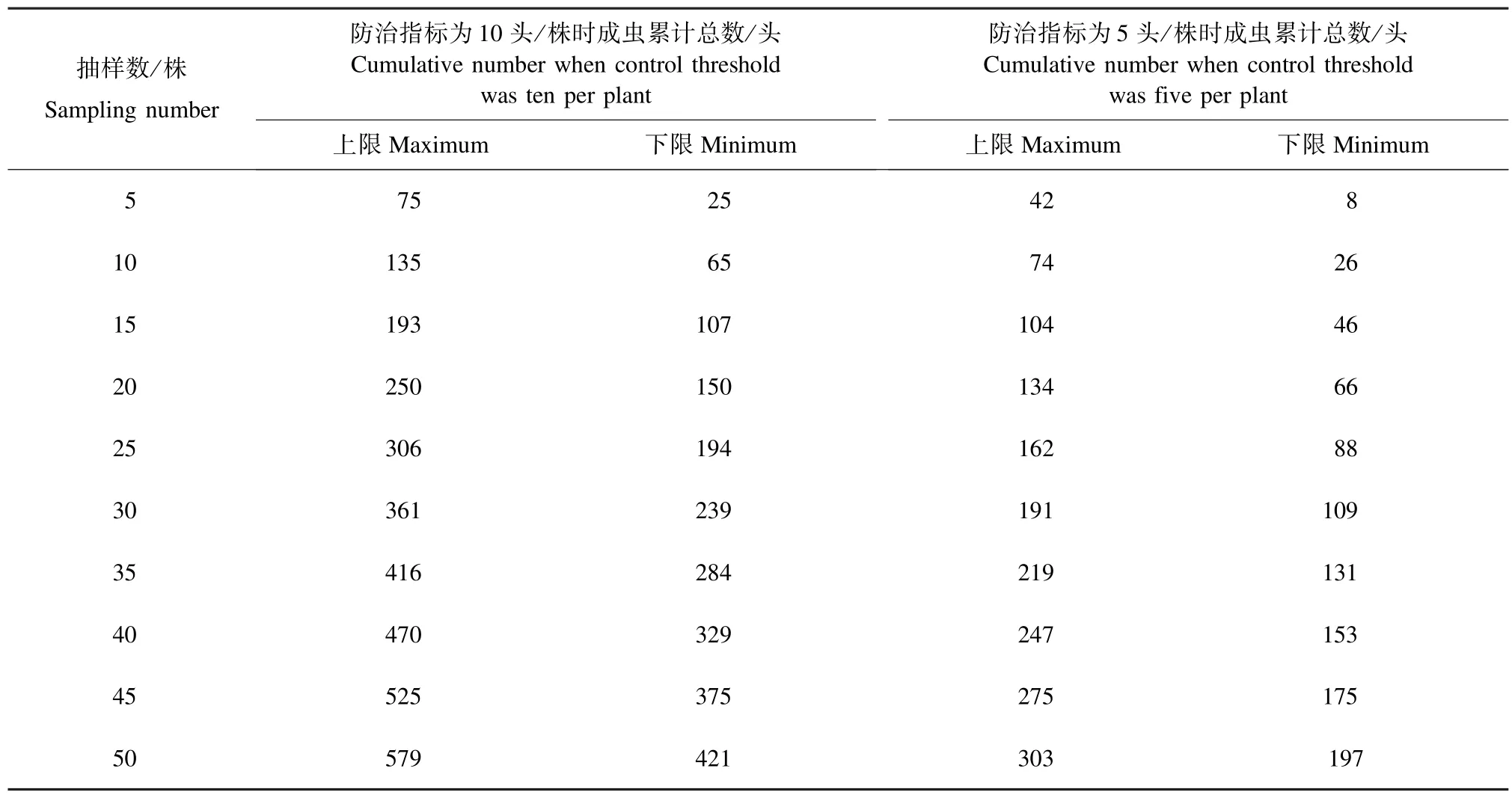
表5 桂花网蝽成虫序贯抽样表Tab.5 Sequential sampling table of E.sigillatus adult
3 结论与讨论
昆虫种群的空间分布格局是种群个体在其生存空间的分布形式,是种群的特征属性。研究昆虫空间分布格局作为种群生态学研究的一项重要内容,不仅能揭示昆虫种群的空间结构和空间格局特征,了解昆虫种群扩散行为及生物学特性,对正确制订调查方法、抽样设计方案、估计昆虫数量动态,制定害虫预测预报、综合治理及防治策略等都具有重要的指导意义[14-16]。
笔者利用DPS数据处理系统对桂花网蝽成虫7个样地的调查结果进行了空间分布型检验分析,结果表明,桂花网蝽成虫在桂花树上的分布属于聚集分布中的负二项分布,具有密度依赖性。桂花网蝽的空间型聚集原因可能与成虫对桂花为害部位(叶片背面)的选择性有关。在此基础上,以桂花网蝽空间分布型和Iwao模型的平均拥挤度的回归关系建立了该种群的理论抽样公式,利用Iwao的序贯抽样模式,制定了简便而适用的序贯抽样表。在今后的虫情调查中,采用该抽样技术研究确定的模型应进行随机抽样。同时根据精确度与工作量,在允许误差和可信区间范围内确定所需最适抽样株数。用序贯抽样表进行抽样时,如调查10株时,防治指标为10头/株,累计虫数超过135头时须进行防治,累计虫数少于65头则不需防治,累计虫数在上限和下限之间时,应继续增加抽样株数以确定防治与否。所以,实际生产中对桂花网蝽进行调查和防治,应考虑抽样数、防治方法、防治效果,兼顾社会效应和生态效应。