微生物生态研究中BIOLOG方法数据分析及R语言实现
2021-04-08范小莉张文馨戴九兰
王 强,梁 玉,范小莉,张文馨,何 欢,戴九兰,*
1 山东省林业外资与工程项目管理站,济南 250014 2 山东省林业科学研究院,济南 250014 3 山东大学环境研究院,青岛 266237
微生物群落在全球生态循环中占据重要地位,也具有重要的环境指示作用[1],从不同层次和角度对微生物群落及生态特征进行揭示一直是学界研究热点[2-4]。自Garland等1991年首次将BIOLOG方法用于微生物群落生理特征检测[5],数十年来该方法在微生物群落和生态研究中得到大量应用,从碳源利用功能多样性的角度刻画了微生物群落生理特征[6-10]。BIOLOG平板包括革兰氏阴性板、生态板、MT板、真菌板、SF-N和SF-P板等多种类型[11],不同平板针对研究对象不同,操作方法不同,但均能产生大量多维数据用以表征微生物群落的功能多样性[12-14]。
在微生物生态研究中关于数据分析方法已有学者专门讨论,但重点多在于理论层面,且对分子生物学范畴关注较多[15-17]。相比分子方法,BIOLOG方法产生数据局限于生理活性,受到关注较少;但由于其数据的多维度、时间依赖、环境相关等特点,同样需要对分析过程进行深入探讨,如数据读取、整理、统计方法选择,统计结果展示,统计结果解释等。然而,由BIOLOG方法的相对小众性,缺少专为此编写的成熟数据处理软件,大量数据处理需要研究者手动完成,耗时费力,容易出错;在应用排序、聚类、差异性分析等方法时,也没有一定标准或参考。不仅如此,在分析中常用的canoco软件[18-19],也容易产生版权问题。已有研究对BIOLOG方法统计分析做过探讨[20],其后不断有研究者联系讨论统计方法选择及实现方式,可见这仍是当前微生物生态研究领域的一个难点。
R语言是为统计和数据处理而诞生的软件,具有优良的数据存储处理、数组运算、统计分析等功能,具有自由、免费、开源等特点[21-22]。其语法简洁优雅,功能强大,在生物信息学、基因数据分析、空间分析、时间序列分析等领域均有优秀表现。当前R官方网站有15000多个扩展程序包(packages),且在不断增加,形成了非常成熟的应用生态[21]。
本研究采用BIOLOG ECO板研究案例,以R语言为工具,从原始文本数据开始,全过程实现数据读取、整理、统计分析,并针对分析结果,结合研究目标给出统计学解释。研究结果对BIOLOG微生物生态研究中统计分析方法选择、提高数据处理效率有直接参考作用。
1 实验数据与分析流程
1.1 实验数据
采用数据为招远矿山周边部分土壤样品测量数据[23],选择6个样品,以样品的BIOLOG ECO板培养数据和重金属有效态含量数据进行分析。
BIOLOG ECO板培养自12 h开始测量,每隔12 h测量一次,至132 h共测量11次。重金属有效态数据作为环境指标,每个样本测定3次重复。
BIOLOG ECO板读数为txt文本数据,重金属有效态数据以csv格式存储。
1.2 分析方法
将BIOLOG数据导入并整理,进行一元特征指标计算、组间差异检验、排序、聚类等分析。应用常见分析方法如AWCD(Average Well Color Density, 平均吸光度)、ANOVA(Analysis of Variance, 方差分析)、MANOVA(Multivariate analysis of variance, 多元方差分析)、NP-KW test(Kruskal-Wallis test, 克鲁斯卡尔-沃利斯检验)、PCA(Principal Component Analysis, 主成分分析)、RDA(Redundancy Analysis, 冗余分析)、CA(Canonical Analysis, 典范分析)、CCA(Canonical Correspondence Analysis, 典范对应分析)、PRC(Principal Response Curve, 主成分响应曲线)、PCoA(Principal Coordinate Analysis, 主坐标分析)、Db-RDA(distanc-based Redundancy Analysis, 基于距离的冗余分析)、NMDS(Nonmetric Multidimensional Scaling, 非度量多维尺度分析)、Mantel test(蒙特尔检验)等;各方法所需数据形式(原始数据或距离矩阵)及相互关系如图1所示。其中排序分析包含限制性排序和非限制性排序;非限制性排序直接探索BIOLOG数据内部规律,限制性排序则纳入环境变量(重金属含量数据),探讨其作为自变量对因变量BIOLOG数据的影响[24]。本文主要对BIOLOG数据分析进行探讨,侧重对群落结构的解释(排序),对环境因子自身的特征探索分析及模型拟合(Y=f(X))分析方法等内容不做涉及。
2 数据导入与整理
2.1 数据导入
BIOLOG方法数据文件应予以合理命名,便于批量读取及整理。数据读取后得到文本格式对象,要提取其中有效信息。本例中有效吸光度在文本的51—58行,构建应用bio.get()函数,读取得到含有66项BIOLOG数据的列表(list);环境指标数据通过read.csv()函数读入(代码见 https://yunpan.360.cn/surl_yPE4EhVDxL3,下同)。
2.2 数据整理
列表是R语言中数据嵌套关系的一种形式,由于读取过程而产生,内容选择可以采用$或[[]]两种形式[25]。将列表中各样本重新命名后转化为数据框(data frame)形式进行计算,31个碳源孔吸光度减去对照孔,负值归零,得到用于分析的数据biolog.31;把样本信息、重复信息、读取时间信息以新列的形式加入数据集中,生成biolog.31.aid,为后续分析及作图做准备。
3 一元特征指数计算和组间差异检验
3.1 一元特征指标
本文一元特征指标指用单一数字表征微生物群落功能特征的指标,如平均吸光度(Average Well Color Density, AWCD)、Shannon多样性指数等。
AWCD为31个碳源吸光度的平均值,是一个有关研究几乎必用的指标,衡量微生物利用碳源的能力[11,20]。R语言中可以使用apply()和mean()函数,针对各行一次性完成。
除了以平均值表征碳源利用综合能力之外,可以从对不同碳源利用能力多样性的角度分析,计算多样性指数[26-27]。大部分多样性指数发源于植物群落研究,可以使用vegan包的vegdist()函数求取[28]。
一元特征指标由单一测量时间信息得出,可以综合多个时间研究其变化趋势。图2为培养期间AWCD值变化情况,同一个时间3个重复均以散点图画在图上,之后进行线性拟合。可以发现,样本2的AWCD值增加最快,表明群落碳源利用功能最强;其次为样本3,样本6、4、1的AWCD值依次降低但区分度不高,样本5培养前期变化较小,后期超过了样本1。
实际研究中,基于研究目标不同,同样也可以对多样性指数等作图,探索变化规律[29]。
由图2可见,84小时附近各样本间读数区分度较好,可以对该时间点读数信息进行深入分析,如差异性检验、排序、聚类等。
3.2 组间差异检验
3.2.1一元指标组间差异检验
为验证84小时各样本AWCD是否有差异,进行方差分析,使用oneway.test()函数。结果表明,P值为0.1698,即84小时6个样本AWCD值间不存在显著差异。进一步检验数据是否符合正态分布,使用shapiro.test()函数,P值为0.04154,即数据不满足正态分布,因此须采用非参数检验考察样本间差异性是否显著。
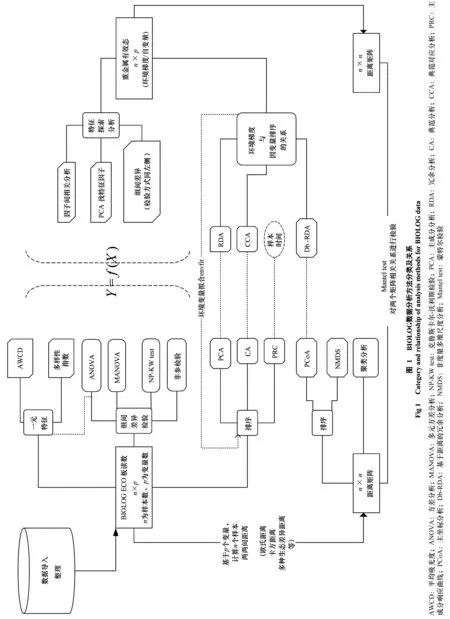
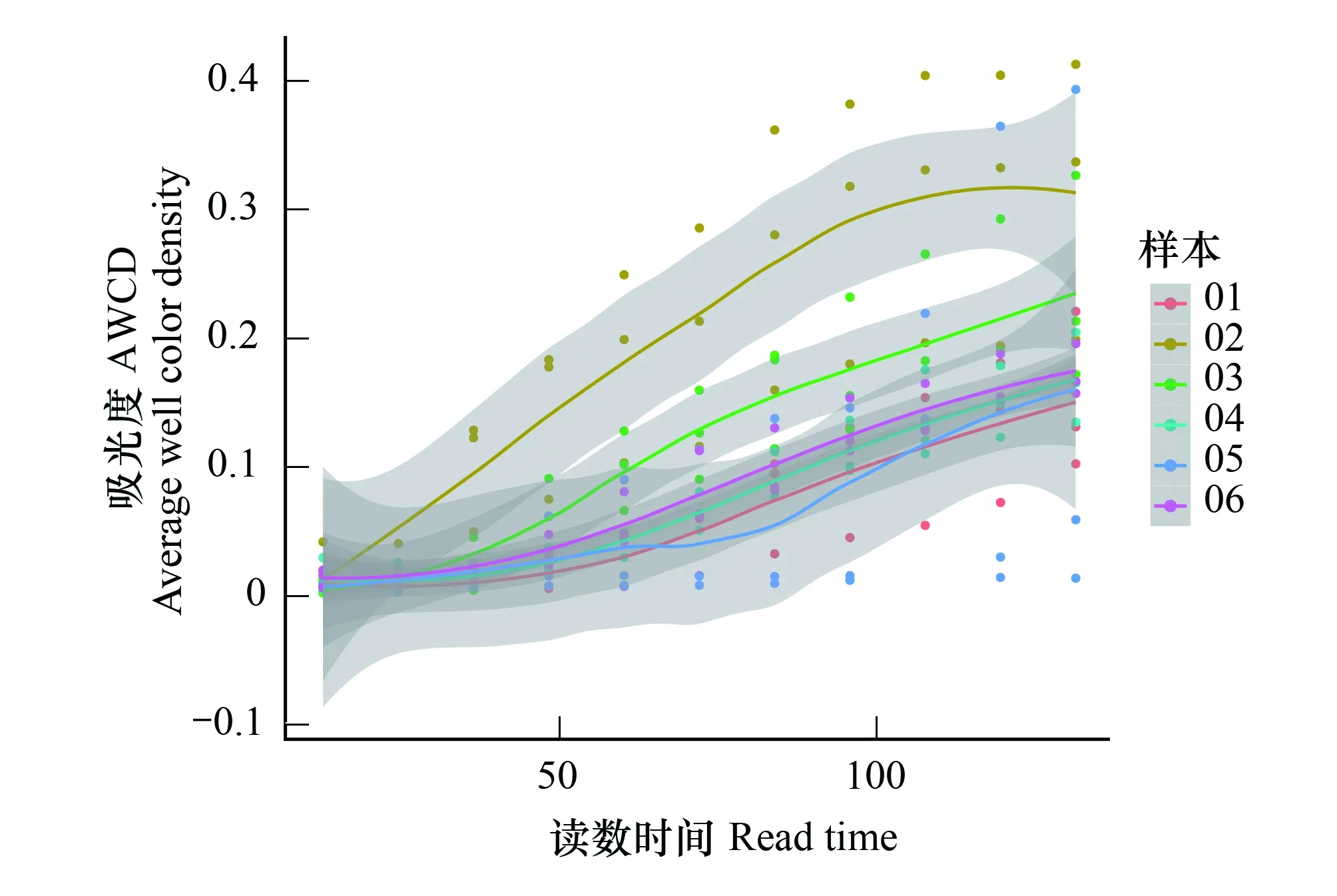
图2 培养过程中AWCD变化趋势Fig.2 Developing trend of AWCD in the culturing period
Kruskal-Wallis检验是方差分析的一个非参数版本。非参数,意味着不假设数据的正态分布形态背景,但它假设各组有相同形状的分布,在BIOLOG数据差异性检验中应用较为合适[30]。使用kruskal.test()函数实现,结果表明,P值为0.05547,接近0.05的阈值,体现一定差异显著性。
3.2.2多元指标组间差异检验
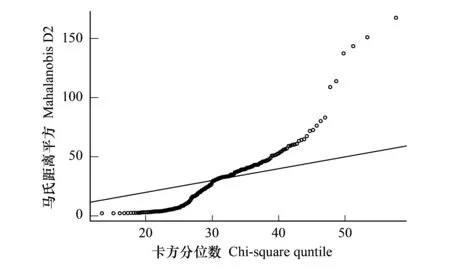
图3 使用QQ图检验BIOLOG数据多元正态性 Fig.3 QQ plot assessing multivariate normality of BIOLOG data
对多元数据的差异性检验常应用多元方差分析(multivariate analysis of variance,MANOVA)。MANOVA有两个前提,一是多元正态性,二是方差齐性。第一个前提说明变量要满足正态分布,可以用QQ图来检验,如果符合正态性,则会呈现一条直线;第二个前提要求各组样本协方差矩阵齐性,可以用M盒检验完成[25]。
应用QQ图检验,发现数据不符合正态分布(图3)。但MANOVA方法有一定分布耐受性,可以计算出结果,显示数据样本间、读数间,均显著差异。
对于不满足正态分布的数据应用非参数检验,采用rrcov包的Wilks.test()函数,方法选择rank;也可以用vegan包的adonis()函数。结果显示,样本间、读数间均有显著差异,表明各样本间BIOLOG吸光度变化具有显著差异。
4 多元分析
4.1 非限制性排序
4.1.1主成分分析
主成分分析法(Principal Component Analysis, PCA)不仅常见于BIOLOG数据分析中,在微生物生态其他类型数据,如基因型、磷脂脂肪酸等分析中也经常用到[26,31]。主成分分析有基于variance-covariance(scale1)和correlation(scale2)两种方式[32]。第一种主要用于相同属性的数据集,用于分析样本间的差异;第二种主要用于不同属性的数据集,如环境因子数据集,单位、数量级都不一样,挖掘变量间的相互关系。
对84小时BIOLOG数据进行主成分分析结果表明,前两个主成分解释63.062%的数据信息,双标图(biplot)将样本和指标放在同一图上,能够清晰表现出各样本之间的差异,本例中将同一样本的3个重复相连表现,红色剪头表征不同碳源吸光度的变化梯度,可以表现出不同样本在碳源吸光度(A2—H4)变化梯度上的分布(图4)。
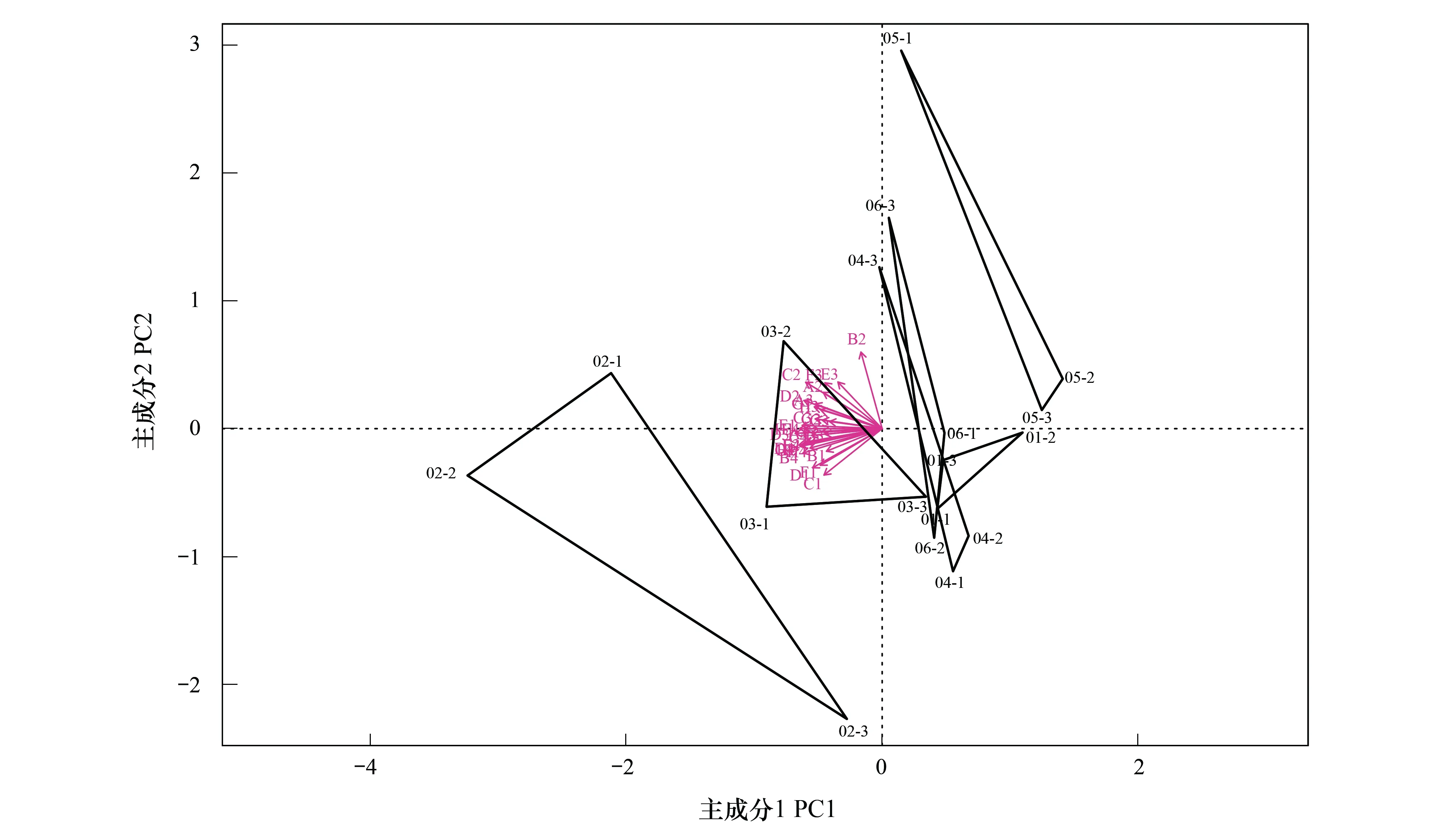
图4 对84小时吸光度进行主成分分析(5个样本重复以-1、-2、-3表示)Fig.4 Principe Component Analysis of BIOLOG data at 84 hour (-1, -2, -3 represent for replications of 5 samples)
要深入分析不同碳源对主成分的贡献率,找到特征碳源,可以通过分析各变量在主成分的载荷(loading)完成[31]。可以使用vegan包中score()函数实现。
PCA是基于线性模型进行的分析,需要数据基本服从正态分布,在分析前应该对BIOLOG吸光度数据是否服从正态分布进行检验。前文对本例BIOLOG数据分析结果表明不服从多元正态分布,因此需要用更加合理的方式进行排序分析。
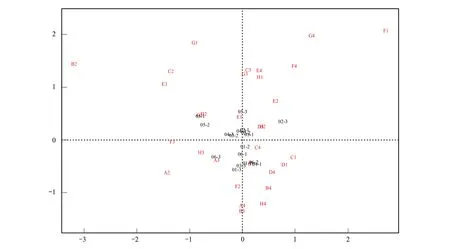
图5 BIOLOG数据84小时吸光度典范分析结果 Fig.5 Canonical Analysis of BIOLOG data at 84 hour A2—H4为31个碳源吸光度
4.1.2典范分析
典范分析(Canonical Analysis, CA)和PCA均为通过计算样本间距离进行的分析,不同在于PCA基于线性模型计算欧氏距离,而CA则基于单峰模型计算χ2距离(卡方距离,Chi-Square distance)。结果表明,CA应用于BIOLOG数据效果不好,前两个轴只能解释39.536%的信息,且对样本区分程度较差,如图5所示,不同碳源指向没有一致性。CA是基于单峰模型的分析[24],在微生物生态研究中应用较为少见。
4.1.3主坐标分析
主坐标分析(Principal Coordinate Analysis, PCoA)与PCA、CA的区别在于距离计算方式。PCA基于线性欧式距离、CA基于χ2距离,而PCoA通过不同的距离矩阵(伴随矩阵,association matrix)来进行分析,从而增加距离计算灵活性,得到更加合理的结果。该方法在分子生物学应用较多,基于基因序列计算距离,分析群落结构在不同处理间的差异[33-35]。
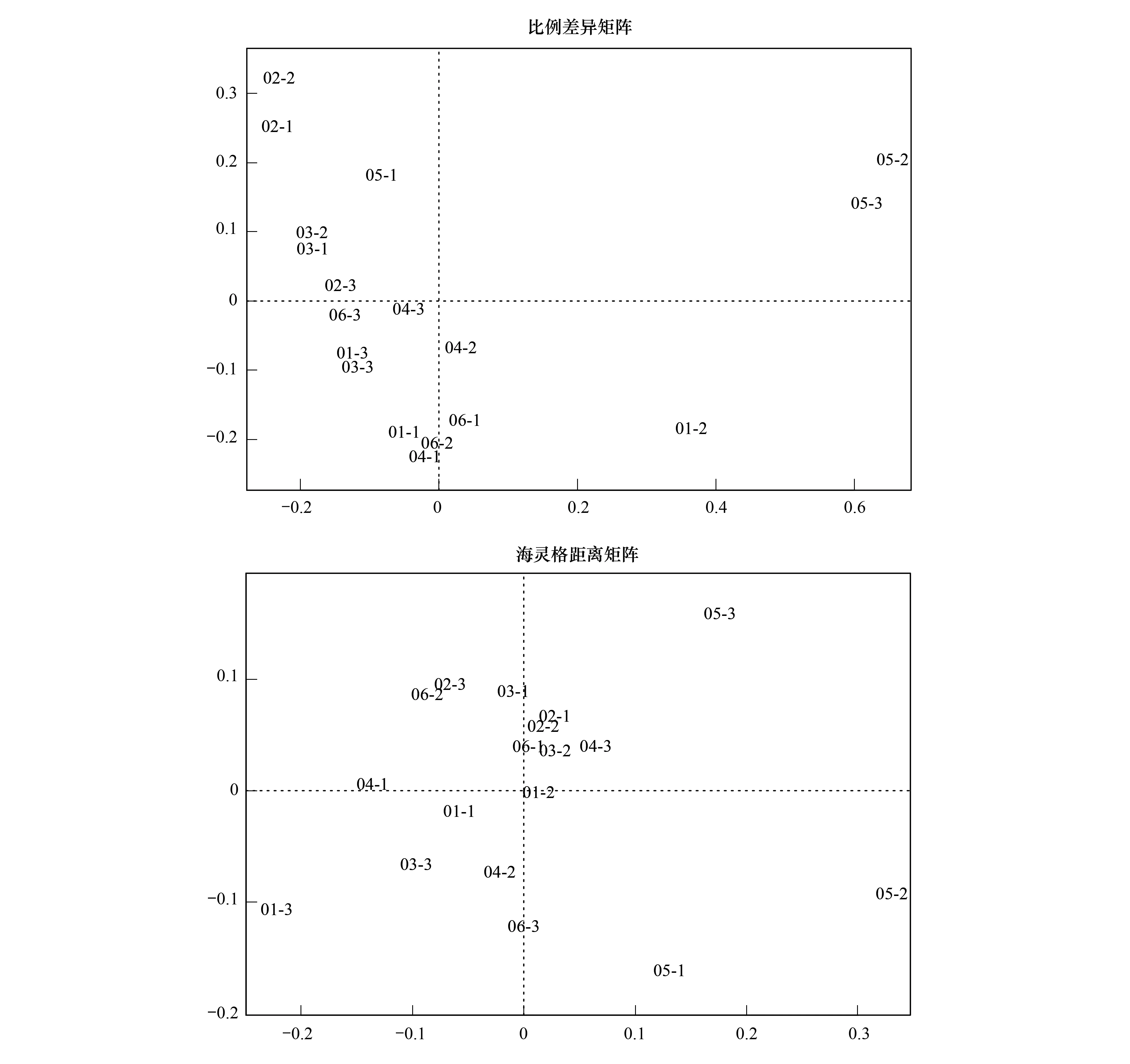
图6 基于比例差异和海灵格距离矩阵的主坐标分析Fig.6 PCoA by Percentage difference and Hellinger distance dissimilarity matrices
分别基于比例差异矩阵(Percentage difference (aka Bray-Curtis) dissimilarity matrices)和海灵格距离矩阵(Hellinger distance)进行PCoA分析(图6)。结果表明,PCoA分析所得样本间差异区分度较高,能发现明确的群落特征;其中比例差异矩阵更能体现出吸光度变化特点,对于样本2、5有更好的区分。海灵格距离矩阵在比例差异矩阵的基础上进一步进行了开方转换,降低了吸光度数据大小的权重,相对不利于发现BIOLOG数据特征。总之,PCoA不依赖数据的分布及线性关系,受分布影响较小,结果更合理稳健,相比PCA更适合用于BIOLOG数据分析。
4.1.4非度量多维尺度分析
PCoA在计算伴随矩阵后,还需要计算确切的样本间距离。但如果只需要考察样本间相对位置,对距离要求不高,则可以采用非度量多维尺度分析/多元尺度分析(Nonmetric Multidimensional Scaling, NMDS)。该方法不仅能基于任意距离矩阵进行计算,还能处理缺失值,应用范围广泛。可以通过vegan包的metaMDA()函数实现,若含有缺失值,可以使用isoMDS()函数[28]。
分析代码见附件,结果如图7所示,对表现样本间特征差异同样有较好的展现效果。该方法和PCoA方法常用于基于核酸序列的排序分析中[36],在基于BIOLOG板的研究中也有应用[37-38]。本方法相比PCoA有更广的应用范围,可以将BIOLOG数据之外的微生物群落信息一并纳入分析,如生物量碳、基础呼吸,测序信息等,理论上都可以一并纳入分析。
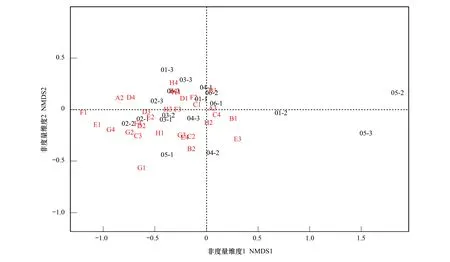
图7 非度量多维尺度(NMDS)分析 (NMDS1、NMDS2)Fig.7 Nonmetric Multidimensional Scaling (NMDS)
4.2 限制性排序
4.2.1环境指标简介
非限制性排序是基于BIOLOG数据特征进行的排序,限制性排序则考虑环境指标等外在因素影响。
本文采用环境指标为土壤重金属有效态含量,分析矿区周边重金属对微生物群落活性的影响,研究不同种类重金属浓度梯度上微生物群落功能多样性的变化。要说明的是,实际研究中,我们不仅考虑了重金属有效态,还测定了重金属全量、若干土壤理化性质,并进行了微生物培养,综合考察微生物群落模式和各方关系。本文为说明分析方法,仅以重金属有效态作为环境因子代表进行示例。
各样本重金属有效态含量见图8,不同重金属在不同样本间含量不同,变化趋势也不一样。为发现重金属含量与微生物之间关系,采用限制性排序进一步分析。
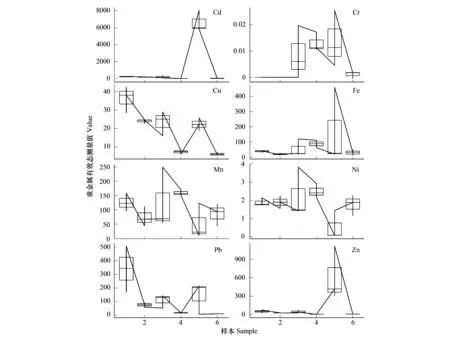
图8 各样本不同重金属有效态含量Fig.8 Available contents of heavy metal in soil samples
4.2.2冗余分析
冗余分析(Redundancy Analysis, RDA)是基于PCA的扩展,通过自变量环境指标对因变量生物指标的多元回归,揭示二者之间的联系和关系[32]。一直有研究将本方法用于环境或其他微生物指标与BIOLOG数据的关系分析[38-39]。
采用vegan程序包的rda()函数,重金属有效态作为自变量、84小时BIOLOG吸光度数据作为因变量进行分析,可知重金属有效态含量可解释BIOLOG吸光度数据中51.89%的方差信息,作图可直观发现各样本在重金属含量梯度上的分布(图9)。可见各样本在Cr和Fe的梯度上分散度最高,可以进一步考虑这两种环境因素在塑造形成目前微生物群落特征过程中发挥的影响。
RDA本质上是自变量环境指标对因变量生物指标的多元回归,自变量也不局限在一组数据,可以同时考察两组数据对BIOLOG的影响,如,将有效态重金属和土壤理化性质同时纳入分析,即偏冗余分析方法(Partial RDA),和偏相关分析类似,可用于控制特定变量的影响。
4.2.3典范对应分析
典范对应分析(Canonical Correspondence Analysis, CCA)是在CA的基础上,基于单峰模型计算χ2距离后,结合多元回归分析因变量与自变量之间的关系。鉴于CA分析BIOLOG数据效果不佳,本文不再深入讨论CCA方法。
实际研究中,有应用CCA的案例。如在方差分解之后,进一步分析不同环境因子与BIOLOG数据间的相关关系[40];在基于分子方法的研究中也有应用,考察化学因素与测序所得操作分类单元(Operational taxonomic units, OTUs)之间的关系[41]。
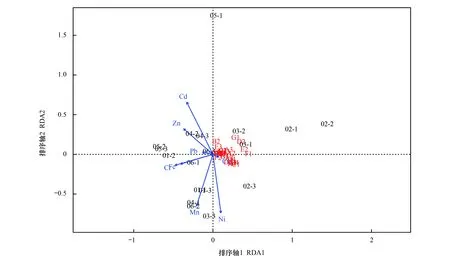
图9 冗余分析 Fig.9 Redundancy Analysis
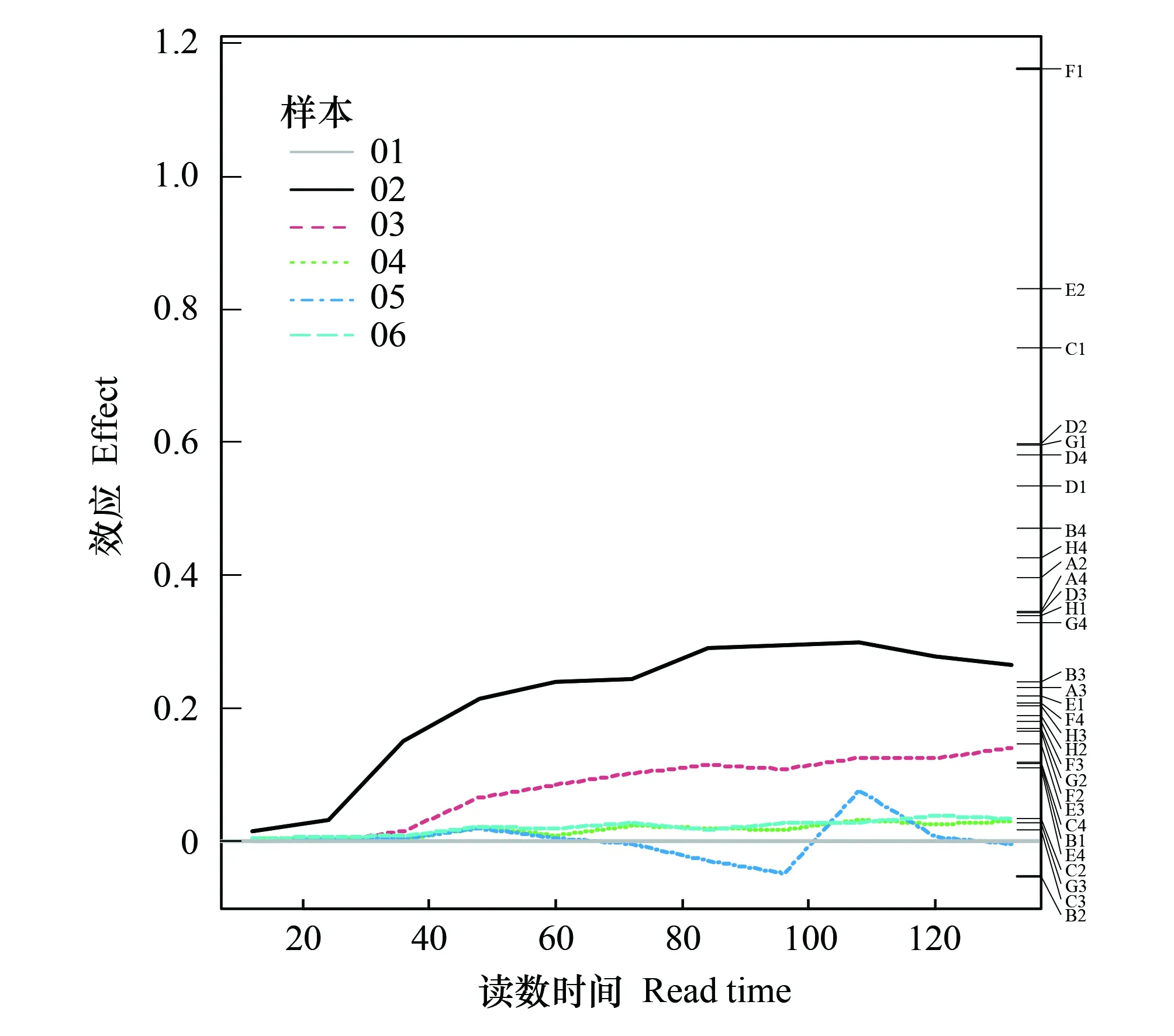
图10 主响应曲线分析Fig.10 Principle Response Curve Analysis
4.2.4主成分响应曲线
主成分响应曲线(Principal Response Curve, PRC)最初设计用来分析实验中具有重复多元数据,可以考察不同设计因素对数据的影响。在BIOLOG数据的分析中,多孔吸光度为需要分析的多元数据,时间和样本均作为重复纳入分析,该方法在BIOLOG研究中的应用类似于AWCD培养曲线变化,但对数据的压缩方式更加精细,且能分辨不同碳源的贡献[42]。本方法虽然归入限制性排序,但不涉及环境因子,限制性是对时间及样本而言。
PRC分析将所有BIOLOG测量数据均纳入分析,按时间将不同样本进行区分。每个样本的3个重复信息压缩到一条线体现出彼此差异,右侧不同碳源表征对差异贡献的大小,分析结果见图10。可以发现本图与AWCD随时间变化有一定相似性,其优势在于处理较为复杂的数据,明确变量的贡献。
4.2.5基于距离的冗余分析
RDA直接将BIOLOG数据和重金属有效态数据纳入分析,分别作为因变量和自变量,并在排序图上以欧式距离反映样本间差异。但有时欧氏距离并不适应所研究生态假设或数据类型,如0—1数据无法计算欧氏距离,不能直接进行RDA分析。针对这种情况,借鉴PCoA方法思想,先计算基于不同距离计算公式的伴随矩阵,如Jaccard系数或Sørensen系数矩阵,然后通过PCoA提取主坐标,并将获得的主坐标矩阵作为响应变量纳入分析,结合环境变量,实现基于距离的冗余分析(distanc-based Redundancy Analysis, db-RDA)[32]。
BIOLOG数据不存在无法计算欧氏距离的情况,但仍可以应用这种适用范围较广的方法,分析效果较好(图11)。
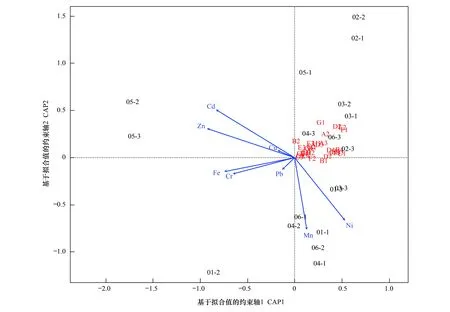
图11 基于距离的冗余分析Fig.11 Distance-Based Redundant Analysis (CAP, Canonical Analysis of Principal coordinates)
4.2.6环境向量拟合
环境向量拟合能得到与限制性排序表现形式相似的图形结果,但内在运算过程不包括多元回归和方差解释的部分,而仅是在非限制性排序的基础上,以多次置换(permutation)求最优解的方式,将环境变量按照梯度进行拟合[32]。
在环境数据能够对生物数据很好的解释时,应优先选用限制性排序,在环境变量能够解释的范畴内解释梯度下群落特征。但如果限制性排序能够解释的信息过低,则限制性排序失去意义,可以用环境向量拟合方法,对梯度下群落特征进行探索(图12)。
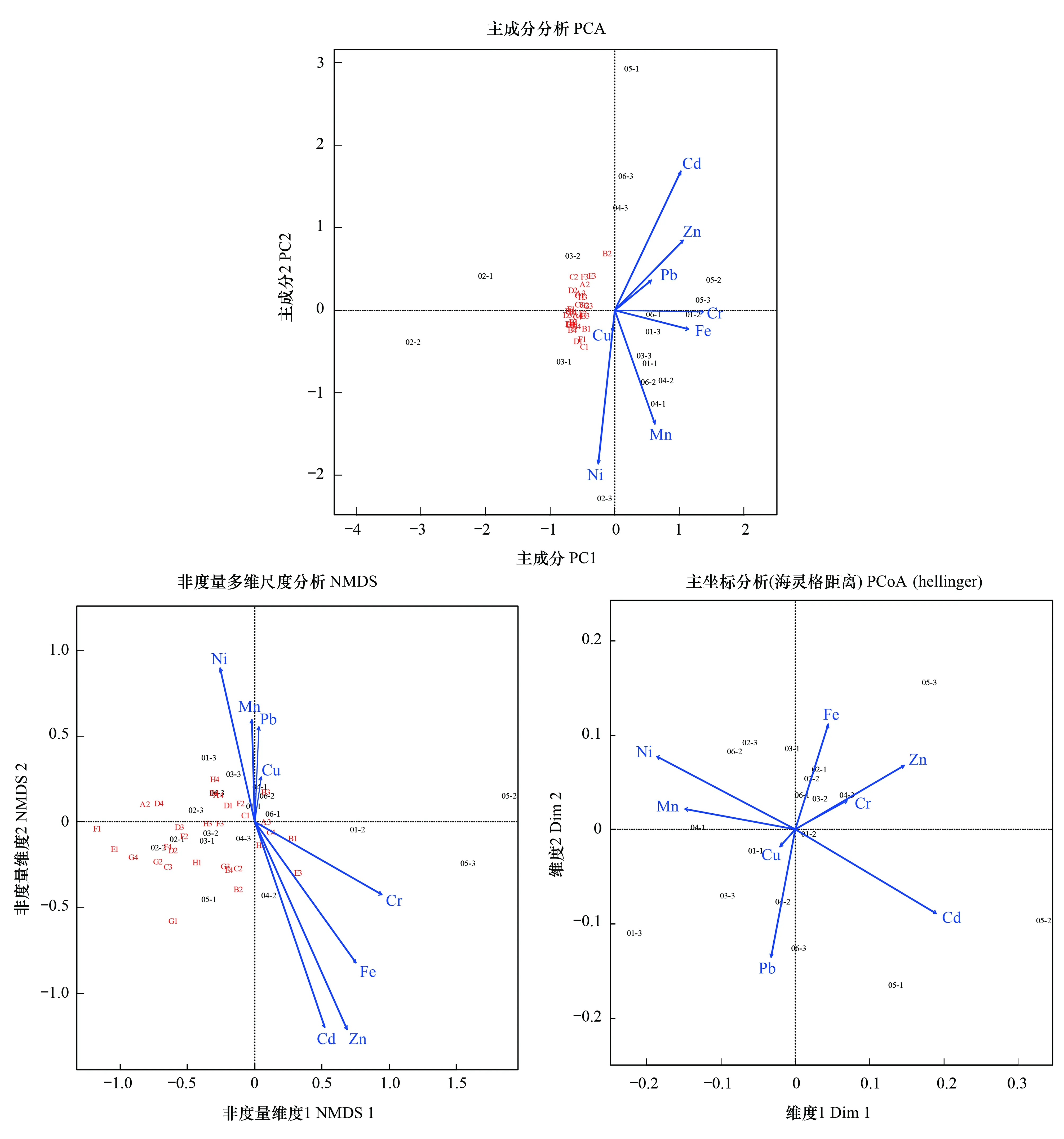
图12 对3种非限制性排序的环境向量拟合Fig.12 Environmental fitting of 3 unconstrained ordination
4.3 聚类分析
聚类分析中,首先要通过变型后的数据建立伴随矩阵,计算距离。伴随矩阵建立以后,主要通过三种方法进行聚类分析:层次聚类(hierarchical clustering)、k平均值聚类(k-means partitioning)和双向联结聚类(two-way joining),聚类结果常以树的形式表现出来。
本例中选择层次聚类中的全连接聚类方法(Complete Linkage Agglomerative Clustering)对84小时吸光度数据进行分析示例,结果如图13所示。需要明确,聚类分析本身是基于数据本身对观测进行分组的方法,并不是严格的统计检验;聚类本身不能代表群落特征,必须结合环境指标进行分析;在表现数据信息方面,聚类反映的信息含量一般比排序要少。
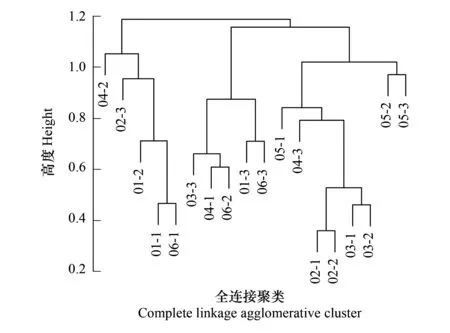
图13 BIOLOG 84小时吸光度聚类分析Fig.13 Cluster analysis of 84 h BIOLOG data
4.4 蒙特尔检验
蒙特尔检验(Mantel test)是对两个矩阵相关关系的检验,检验相关性是否显著。这种方法多用于植物生态学研究,考察不同植物群落间相关关系。微生物生态研究中,在基于测序的方法中也有采用,如在限制性排序后,进一步分析环境因子与细菌与真菌的关系[43]。
蒙特尔检验的原假设是两个矩阵间没有相关关系,较小的P值证明拒绝原假设,即矩阵间存在相关关系。对84小时BIOLOG吸光度数据和重金属有效态数据进行相关性分析,结果表明,不论采用Spearman还是Pearson方法,P值均为0.002,即二组数据均存在显著相关关系。这也说明上述针对两组数据做进行的各种分析是合理有依据的。
5 讨论
本文在R语言环境下进行了AWCD值、多样性指数计算,组间差异检验,排序、聚类和蒙特尔检验等分析。其中AWCD值、多样性指数描述样本内吸光度的特征,属于生态研究中的样方内α多样性,排序则进行样本间特征比较,考察β多样性。在传统生态学研究中,这些多样性指标可以用来考察物种更新速率、物种周转变化等规律;微生物生态中得到这些指标,也能对群落研究有所借鉴和启发。分析过程中快速、准确的计算方法,能解放出更多精力用于思考科学问题,会对研究工作走向深入提供助力。
实际研究中还有很多可以用于BIOLOG数据分析的方法,篇幅所限没有纳入。如针对培养曲线进行方程拟合并分析参数、Pathway 富集分析、相似性分析(Analysis of similarities,Anosim)、典范变异分析(Canonical variate analysis, CVA)、去趋势对应分析(Detrended correspondence analysis, DCA)、BIOLOG指标作为因变量与环境指标的建模等,均可结合研究目标选用[44-45]。如对原生函数图不满意,可提取分析结果中关键数据,使用R语言中ggplot2程序包[46],或导入Origin等作图软件中作图。附件中也给出使用ggplot2包对PCA结果作图示例,供参考。
