地震荷载下长短桩复合地基的群桩效应系数分析
2021-04-08林智勇
林智勇
(1. 福建工程学院岩土工程研究所,福建 福州 350118;2. 福建省工大工程设计有限公司,福建 福州 350014)
0 引言
通常情况下,大型建筑物的桩基础大多采用端承桩和摩擦桩。在桩基础中采用预制桩时,即使桩的竖向承载力足以承受建筑物的均布荷载,但如果桩的横截面积不能满足抗震性能要求,则必须在地基中再添加更多桩基(图1)。诸如此类情况按要求应该增加规格相同的桩基(桩径、长度、截面积、强度等),往往导致了桩基础的造价一般会超出工程预算,也会导致桩基的竖向承载力没有得到有效的利用,从设计的角度来看并非合理。

图1 长桩基础Fig.1 Long pile foundation
近年来,岩土工程界针对这个问题提出长短桩复合桩的施工方案[1-5]。目的是将超过长桩抗震承载力的地震荷载(主要是水平向)由短桩来分担,从而减少地震时长桩所受的剪力和弯矩(图2)。这种复合桩基础结构与传统的桩基础相比,更加明确了长桩和短桩的功能分担,从而以达到较为合理的设计目标。

图2 长短桩复合基础Fig.2 Long-short pile composite foundation
以往的研究表明,在复合桩基中,短桩展现出具有降低长桩所受剪力和弯矩的效果[6]。在长短桩复合桩基地震液化分析结果表明,在长桩之间设置短桩,可使长桩的桩头弯矩减少约30%[7]。部分研究利用地基-桩-上部结构组成的模型,对长短桩复合基础进行了振动台模型试验或有限元数值分析,结果表明,短桩减轻了长桩的水平承载力从而降低了桩头弯矩[8-9]。本研究也表明了采用超短桩可以达到减少长桩的剪力和弯矩的效果,虽然在以往的研究事例中有提到短桩对长桩的水平承载力和桩顶弯矩有降低作用,但目前对短桩和长桩互相影响程度进行定量评价和验证的研究仍不够充分。
在复合桩基中,由于短桩是配置在相邻的长桩之间的,所以在大多数情况下采用群桩基础。关于桩的水平承载力等计算公式,主要都是针对桩长和桩径一致的情况,而不是长桩和短桩混合在一起的复合桩基基础。因此,在进行长短桩复合桩基设计时,有必要制定一种新的计算方法,通过桩径、桩长、桩间距等因素来评价群桩系数。本研究提出了在长短桩复合桩基中水平方向群桩效应系数评价方法,并通过与模型试验结果对比,验证了其有效性,并探讨了长短桩复合桩基对成本的降低效果。
1 长短桩复合桩基水平方向上的群桩效应系数
1.1 短桩的长度对群桩效应系数的影响
在长短桩复合基础的群桩效应系数评价中,除了桩径和桩间距外,还需考虑到短桩的桩长影响。在这里使用静态有限元分析对短桩的长度及其对群桩效应系数影响进行了讨论。
1)静态有限元分析
对打入弹性地基的钢管桩进行数值模型建立,桩头限制旋转,在桩端自由的条件下,对桩头施加一个水平方向上的力,由桩头水平位移10 mm时的水平力算出地基反力系数,由此来评价相邻桩之间的影响。在数值模型中,设定钢管桩和地基都为弹性的,然后在钢管桩与土接触的地方包括桩尖在内放置接触元件。假设这里使用的接触元件只传递压力(无拉伸)而不传递摩擦力(与钢管桩的摩擦系数为0)。使用数值软件ABAQUS对模型进行分析[10],分析范围为从外侧桩的中心开始的前后和横向两个方向的10B(B为长桩直径),深度方向为15B范围。长短桩数值模型配置见图3,将群桩以单排布置,各长桩之间的距离为6 m并在长桩中间设置短桩。

图3 数值模型分布Fig.3 Numerical model distribution
在模拟时,将长桩的直径×厚度×长度分别设定为1000 mm×20 mm×20 m,短桩的直径×厚度分别设定为600 mm×12 mm、1000 mm×20 mm、1200 mm×20 mm,长度分别设定为3 m、5 m、10 m。虽然地基刚度设为1000 kN/m2和10 000 kN/m2,则大致相当于N值为1或10的地基土。水平方向的群桩效应系数的计算方法:首先,以一根长桩模型为基准得到水平方向的地基反力系数,然后在间隔为6 m的3根长桩之间放置2根短桩的模型来进行数值分析,通过桩头水平受力和桩头位移来计算群桩效应系数。
2)由静态有限元分析结果来计算群桩效应系数
根据每根桩的桩头水平力H和桩头的位移δ计算出长短桩复合桩基中的水平群桩效应系数η。首先,假设长桩受挠度位移、短桩受挠度或刚性位移影响,见图4。

图4 短桩的变形特征Fig.4 Deformation characteristics of short pile
桩的特征值为β,桩长为L,当β·L≤1时,假设短桩所受位移分布为刚性位移,当β·L> 1时,则为挠度位移。另外,在挠度影响下,桩头所受水平力为桩头水平力H挠度,刚性位移时,桩头水平力为H刚性。假设水平群桩效应系数为η,单桩水平方向的地基反力系数为k,桩头位移为δ,βi·Li>1时桩i的桩径为Bi,弯曲刚度为EIi,则桩i桩头水平力Hi可由公式(1)表示:
(1)
但βi为桩i的特征值由公式(2)表示:
(2)
设Bj为桩径,Lj为桩j的长度,βj·Lj≤1时,桩j的桩头水平力Hj表示为公式(3):
Hj=ηk·Bj·Lj·δ
(3)
全桩头的总水平力为Hall,各桩的水平力分别为H1,H2,...则:
Hall=H1+H2+H3+…=∑Hi+∑Hj
(4)
由于各桩的桩头位移量δ相同,故可将公式(4)转化为公式(5):
(5)
分析结果及计算出的群桩效应系数见表1。

表1 静态有限元数值模拟结果和群桩效应系数Table 1 Static finite element numerical simulation result and pile group effect coefficient
1.2 群桩效应系数的评价与短桩的影响系数
由于长短桩复合桩基中水平方向上的群桩效应系数η介于仅对长桩进行评价的群桩效应系数η长桩和对包括短桩在内的所有桩进行评价的群桩系数η全桩之间,所以应通过公式(6)中短桩的影响系数来考虑短桩长度带来的影响。
η=η长桩-χ(η长桩-η全桩)
(6)
χ为短桩的影响系数。由静态有限元分析结果所求得的短桩影响系数χ和β·L的关系见图5。这里桩的特征值β由公式(7)求得:
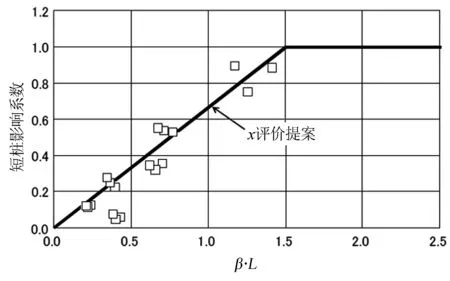
图5 短桩影响系数与β·L关系Fig.5 Relationship between short pile coefficient and β·L
(7)
k为单桩水平向地基反力系数;η为水平向群桩效应系数;B为桩径;EI为弯曲刚度。上述短桩的影响系数χ见式(8):
(8)
由有限元模拟结果得到的群桩效应系数和由公式(6)算出的群桩效应系数的比较结果见图6。在计算特征值β时,桩的桩径和抗弯刚度为所有桩的平均值,L为短桩的长度。

图6 群桩效应系数对比Fig.6 Comparison of pile effect coefficients
2 通过动态离心模型试验的对比验证
2.1 离心模型试验的概要和结果
长短桩并用的动态离心模型实验土箱见图7。实验中填充相对密度为60%砂土的土箱中进行,模型重力场为50 g。试验结构概要见表2。图8展示了实验模型概要图,作为试验用的长短桩均采用铝合金制,短桩的直径和弯曲刚度和长桩一致,实验分为两个情况进行(即Case1和Case2),Case1中桩间距为6B(B为桩径),Case2中桩间距为3B,输入地震波的最大加速度分别为0.90 g(大)、0.35 g(中)、0.14 g(小)。表3为剪力达到最大时的试验结果,表4为长桩的桩头产生最大弯矩时的试验结果。
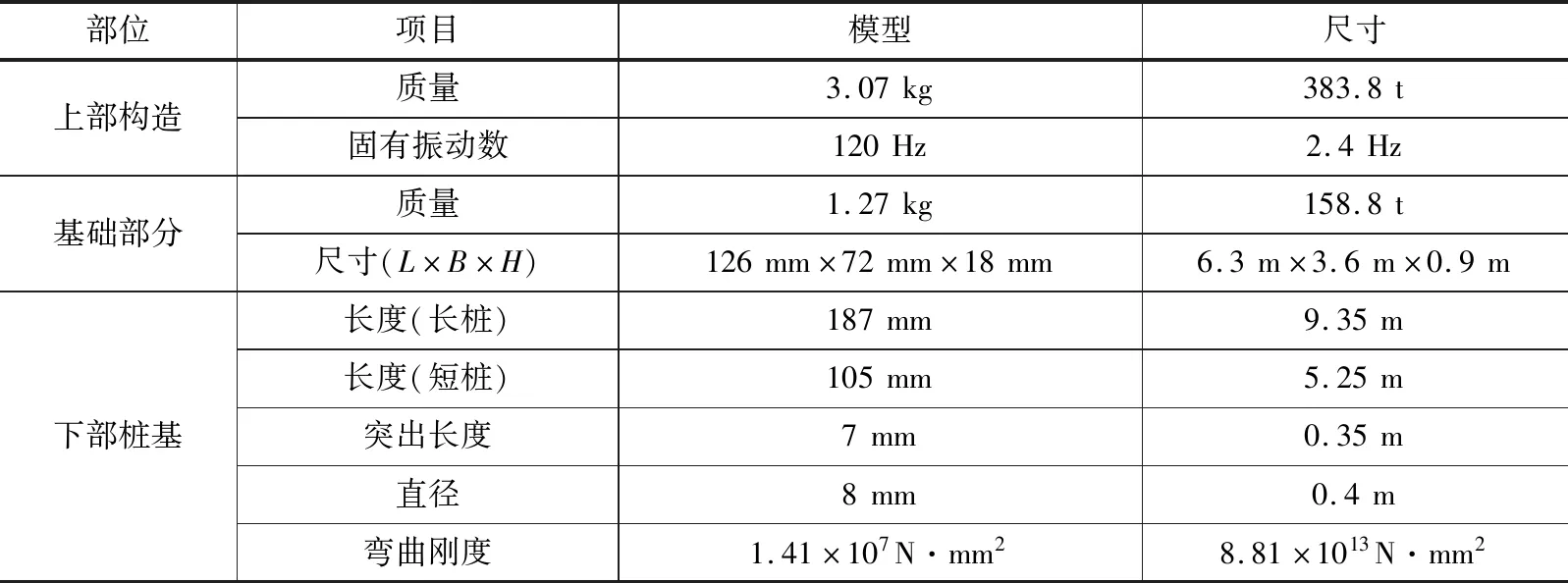
表2 结构模型概要Table 2 Structural model outline

表3 实验结果(最大剪力时)Table 3 Experimental result(maximum shear force)

表4 实验结果(最大弯矩时)Table 4 Experimental result (maximum bending moment)

图7 离心模型实验土箱Fig.7 Soil box in centrifugal model experiment

图8 实验模型概要图Fig.8 Schematic map of the experimental model
2.2 离心载荷试验的静态数值模型分析和常数设定
本数值模型基于剪力和弯矩达到最大时的梁-弹簧模型的静态模型分析模拟离心载荷试验。设定土的重度γ=14.5 kN/m3,内摩擦角φ=38°,泊松比ν=0.35,并假定各层剪切波速度与垂直有效应力成正比。桩侧的水平方向地基弹簧效应根据Francis公式(9)计算出的单桩水平向弹簧效应常数作为初始刚度[11],地基反力与水平位移的关系由双曲模型公式(11)确定并以Broms极限地基反力式(10)为上限[12]。根据公式(6)和公式(8)计算各复合桩基类型的群桩效应系数。各层剪波速度和群桩效应系数见表5。
(9)
(10)
(11)
其中,Kfsi为i层地基土中单桩单位长度的水平方向地基弹簧效应常数;Esi为i层地基土的杨氏模;νsi为i层地基土的泊松比;B为桩的直径;EpIp为桩的抗弯刚度;Pmax为i层地基土桩周弹簧效应的极限水平地基反力;σ0为有效上部荷载;Kp为被动土压力系数;cu为不排水抗剪强度;l为桩的长度;Pi为i层地基土的水平方向地基反力;δi为i层地基土中桩的水平位移量。地基表层的非线性增长特性曲线由反应谱法计算得到。通过一个周期地震加速度傅里叶频谱近似求得一周期地基的非线性特性。地基的非线性特性(剪切弹性模量、衰减常数、剪切波波速等)是根据G/G0-γ和h-γ曲线并利用剪切振动模型,从各点相对位移的有效应变反复计算得出。将表5中各层的VS值作为剪切波波速的初始值来计算出地基响应位移(图9)。

图9 各层地基响应位移Fig.9 Response displacement of each layer of the foundation
2.3 数值分析结果
图10为长桩所受剪力的对比(最大剪力时),图11为长短桩所受剪力的总和的比较(最大剪力时),图12为桩头弯矩的比较(最大弯矩时)。Case2(长短桩复合桩基)中,长桩和短桩所受的剪力随着地震幅度的增加而呈增大的趋势,该数值分析结果和实验结果是一致的。桩头弯矩在小幅度震动时Case1(长桩)和Case2(长短桩复合桩)的分析结果和实验结果保持一致,中幅时Case1和Case2的数值分析结果都比实验结果稍大。大幅震动时Case1的分析结果比实验结果稍大,Case2的分析结果和实验结果大致相同。

图10 长桩所受剪力(最大剪力时)Fig.10 Shear force of long pile(maximum shear force)

图11 长短桩所受剪力的总和Fig.11 The sum of the shear forces on long and short piles
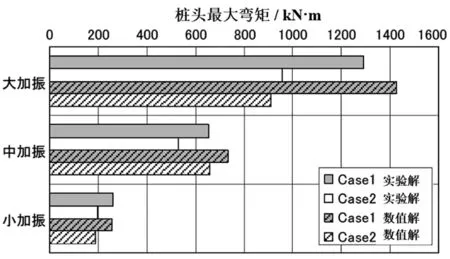
图12 桩头弯矩(最大弯矩时)Fig.12 Pile head bending moment(maximum bending moment)
3 在模型建筑物上的效果验证
以钢筋混凝土造的14层楼作为研究对象。对象地面表层附近的水平刚性较小,坚实层在距离地表40 m深的位置。柱下设置的长桩采用高承载力钢管桩,需要坚实层打入一定长度。
3.1 水平方向的地基弹簧效应和桩截面力的计算模型
1)水平方向的地基弹簧效应
在对象地面i层的桩周的水平方向的地基弹簧效应利用表5所示剪切波速度,以及公式(9)计算出的单桩水平弹簧常数作为初始刚度,根据公式(10)和公式(11)设定地基反力-水平位移关系。在本次验证中,不考虑输入地震运动引起的剪切波速度降低。

表5 各地层剪切波速和群桩效应系数Table 5 Shear wave velocity and pile group effect coefficient of each rock layer
2)群桩效应系数
由式公(6)和公式(8)计算在长桩地基和长短桩复合桩中水平方向的群桩效应系数(表6)。

表6 水平方向群桩效应系数Table 6 Horizontal group pile effect coefficient
3)桩截面力的计算模型
将桩头条件设定为旋转限制,桩底条件设定为自由,然后依据梁-弹簧模型算出桩截面力。
3.2 设计结果
1)桩布局
长桩地基和功长短桩复合桩布局配置见图13、图14。

图13 长桩基础布局配置Fig.13 Long pile foundation layout configuration

图14 长短桩复合桩基础布局配置Fig.14 Long-short composite pile foundation layout configuration
2)短桩对长桩截面力减少的效果以及成本效益
长桩的水平受力和桩头弯矩的比较结果见表7。由于短桩吸收了水平剪力,长桩的水平受力降低了24%,桩头弯矩降低了25%。包括在施工费在内,长短桩复合桩基础降低了约7%的成本。

表7 长桩承受水平力及桩头弯矩Table 7 Horizontal force on long pile and pile head bending moment
4 结论
在本研究中,使用大量静态有限元分析来推导长短复合桩基中水平群桩效应系数的计算公式。为了验证其合理性,研究进行了动态离心模型试验,并与使用模拟梁-弹簧模型的静态模拟进行了比较。本研究方法的特征之一短桩的效果由桩的特征值β决定,因此也可以同时考虑到地基弹簧效应的非线性特性对群桩效果的影响。从数值分析结果和实验结果的比较可以总结出以下结论:
1)根据地基的软硬程度和弹簧刚度来设定群桩效应系数,其结果与实验数据有较好的一致性。
2)无论震级大小,通过这种评价方法都能给出较为普遍合理的系数。
3)由于桩截面力和变形与地基常数有很大的关系,因此,在实际应用中,此方法需要进行适当的常数设置。此外,本研究方法是基于由剪切波速度得到的水平方向地基弹簧效应,因此在实际设计中宜采用勘测得到的地基参数(剪切波速度Vs、密度ρ、泊松比ν等)。
4)本研究的目的是在地震时由打设在柱下长桩之间的短桩分担水平力,以减小长桩所受横截面力。符合竖向承载力和桩侧摩擦力设计的前提下,对于成本控制,表层地基的水平刚度越小,在长桩的长度较长埋深较大的情况下,成本降低效果好。在长短桩复合桩地基中,如果能根据地表的地质条件,适当地设置直径、长度、短桩数量等,就可以进行更合理的设计。
