基于背景矩阵减法的探地雷达杂波信号抑制方法研究

2021-04-08钟景阳王洪华

矿产与地质 2021年1期

彭建，钟景阳，白洁，孟旭，王洪华，刘海

(1. 中国建筑第八工程局有限公司，上海 200135；2. 广州大学土木工程学院，广东广州 510006；3. 桂林理工大学地球科学学院，广西桂林 541006)

0 引言

探地雷达(Ground penetrating radar，GPR)是一种高效、高分辨率的浅层地球物理勘探方法，其原理是利用高频宽带电磁波(10 MHz～10 GHz)对地下目标或者物体内部进行探测。通过发射天线向待探测目标发射高频电磁波，之后利用接收天线采集回波信号，并分析其双程走时、振幅和相位等信息来解析目标体的空间分布及物理性质。探地雷达方法相比其他地球物理勘探方法具有操作简单、分辨率高、实时成像、适应性强等优点，目前已被广泛应用于土木工程检测[1-3]、深空探测[4]、地质调查、考古勘探[5]等领域。

在实际探测中，探地雷达接收到的信号不仅包含地下目标产生的回波信号，还存在着各种杂波，如直达波、耦合波、环境干扰和随机噪声等。目标信号往往会被杂波信号掩盖，增加了对目标体的辨识难度。杂波信号的形成有内部因素和外部因素，内部因素是雷达采集系统自身引起的，而外部因素是由于外界环境引起的，比如，探地雷达发射的探测信号从空气进入地下时，由地表面引起的杂波，由于地下介质非均匀随机分布引起的地下介质杂波，同时发射天线和接收天线之间还存在天线互耦杂波，雷达系统在接收和存储数据时也会引入一定的噪声等[6]。

杂波抑制是探地雷达数据处理的必要步骤，目的是去除雷达数据中的非目标成分，使目标信号得到增强。目前常见的探地雷达数据杂波抑制方法大致可分为基于杂波模型、基于信号统计和基于子空调投影三类方法。其中，基于杂波模型的减平均道法[7]和Scale and Shift法[8]较为常用，但由于计算方法简单，杂波抑制效果不理想。基于信号统计的最大似然估计法[9]、卡尔曼滤波法[10]，以及Dahan Liao[11]提出的统计极化法、Fawzy Abujarad[12]提出的独立特征分析法等算法仅对抑制地表不平整时产生的杂波有较好的效果，而且这些算法的稳定性不高，对所使用的参数比较敏感。基于子空间投影的奇异分解法[13]和主成分分析法[14]较其他算法具有较强的杂波抑制能力，但算法参数的选取尤为关键。近年来有学者提出使用背景矩阵减法对视频和图片中的噪声进行处理，获得了较好的结果[15]。本文将背景矩阵减法应用于探地雷达信号杂波抑制，并将减平均道法、奇异分解法、背景矩阵减法以上三种方法分别对钢筋混凝土结构探测和地下管线探测两种情形的仿真数据和一组实测数据进行杂波抑制处理，并对结果展开对比分析。

1 杂波抑制方法

1.1 减平均道法

减平均道法是探地雷达数据处理中最常用的杂波抑制算法。这种算法假设杂波信号沿测线方向基本不变，即具有大致相同的波形、振幅和时延。通过对构成 B-scan 数据的每道 A-scan雷达数据沿横向进行平均，得到平均道，之后将每道 A-scan 数据减去平均道来消除杂波信号。假设探地雷达的 B-scan 数据矩阵为A(A为M行N列的矩阵)，S表示杂波抑制后得到的目标信号矩阵估计，减平均道法见数学公式(1)：

i=1，2，…，M；j=1，2，…，N

(1)

1.2 奇异分解法

基于子空间投影的奇异分解法是将矩阵分解为3个矩阵相乘的形式，其中分解的矩阵中包括2个正交矩阵和1个对角阵。

对于M×N的雷达数据，M代表采样点数，N代表道数，雷达数据的矩阵表示形式见公式(2)：

A=(xi，j)(i=1，2，…，M；j=1，2，…，N)

(2)

式中：xi，j代表在第i行，第j列的值。

矩阵A奇异分解表示可写成

A=UDVT=[u1…ur…um]·

(3)

式中：U是M×M的正交矩阵，其每列为协方差矩阵AAT特征向量ui，V是N×N正交矩阵，其每列为协方差矩阵ATA的特征向量vi，D是由r(r是A的秩)个元素组成的M×N的对角矩阵，其元素从大到小排列，即σ1≥σ2≥…≥σr≥0，σi称为矩阵A的奇异值。将式(3)展开得，

(4)

(5)

式中：k是一个小于维度M和N的正整数。将式(5)代表的杂波信号去除即得到处理后的雷达数据。

1.3 背景矩阵减法

背景矩阵减法将探地雷达数据作为矩阵处理，矩阵的列数对应雷达数据的道数，行数对应于雷达数据的采样点数。背景矩阵减法通过计算仅由杂波组成与雷达数据矩阵相同尺寸的背景矩阵，然后将其从原始雷达信号矩阵中减去，达到抑制杂波信号的目的。

背景矩阵减法的实现过程包括以下步骤：

1)在GPR剖面数据矩阵每个采样点布置一维水平窗口，窗口长度取决于需要处理的雷达数据道数；

2)计算窗口内雷达数据的平均值，见公式(6)、(7)：

(6)

L=N×α

(7)

式中：N为一维水平窗口的宽度；α为裁剪系数，不大于0.5；L为需要排除数据点数；ai为第i个数据点对应雷达信号值。

3)排除窗口内与Aα极性不同的样本，具体表达式见公式(8)：

(8)

4)根据步骤3)中剩余的数据值与经过α修剪后的数据均值接近程度进行加权，其中越接近的数据值将获得更高的权重，权重系数记为s，见计算公式(9)、(10)：

(9)

(10)

5)对样本权重进行归一化，见公式(11)：

(11)

6)每个样本乘以相应的归一化权重并求和，将结果值作为选取的一维窗口数据点的背景噪声，见公式(12)：

(12)

7)沿水平和垂直方向滑动窗口，并将元素值分配到相应的位置，创建与雷达数据矩阵具有相同维数的背景矩阵。

背景矩阵减法计算过程中涉及的参数有窗口长度、裁剪系数α、加权系数s，以上参数与具体雷达数据相关，需要根据要处理的GPR数据来决定。但是，经验表明，选择错误的参数只会增加获得满意结果所需的迭代次数，并不会影响最终结果。

2 数值仿真试验

为了对比以上三种算法的杂波抑制效果，首先进行了混凝土中钢筋探测和地下管线探测的数值仿真试验，并对仿真数据进行处理。

2.1 钢筋混凝土结构探测

本小节对探地雷达在钢筋混凝土结构钢筋探测进行仿真，建立了仿真模型(图1)，模型大小为3 m×0.5 m，其中混凝土的相对介电常数为6，钢筋埋深为5 cm。离散网格数为1500×250，网格大小为0.002 m。激励源采用中心频率为2 GHz的雷克子波，采样时窗为8 ns。利用时域有限差分法进行仿真，天线收发间距为0.05 m，获得575道信号，道间距为0.005 m。

仿真得到的探地雷达剖面(B-scan)见图1b，从图1b中能够看到较强的直达波信号、地表反射以及钢筋产生的双曲线反射。为了对比分析杂波抑制效果，使用减平均道法、奇异分解法、背景矩阵减法三种算法分别对数据进行处理，结果见图2。背景矩阵减法去除直达波效果最好，处理后的图像几乎无虚假反射产生。对于减平均道法和奇异分解法，由于算法存在缺陷，计算杂波信号存在偏差，导致在钢筋位置产生虚假信号。选取图2红色虚线位置绘制单道信号(图3)，读取目标振幅后计算减平均道法、奇异分解法、背景矩阵减法与原始数据中振幅差异分别为-7.2%，-9.2%，8.2%。可以看出三种方法中背景矩阵减法处理后目标信号保真度较好，而另两种算法会对目标信号造成衰减。

图1 钢筋混凝土仿真模型(a)和钢筋反射雷达剖面(b)Fig.1 Reinforced concrete simulation model (a) and rebar reflection radar profile (b)

图2 杂波信号抑制后钢筋反射雷达剖面Fig.2 Rebar reflection radar profile after clutter suppression(a)减平均道法(average trace subtraction) (b)奇异分解法(singular value decomposition) (c)背景矩阵减法(BMS)

图3 杂波信号抑制后钢筋单道反射信号Fig.3 Rebar single channel reflection signal after clutter suppression

2.2 地下管线探测

图4a为具有分层结构的空心塑料管道数值模型。模型的大小为3 m×1.8 m，双层背景介质的相对介电常数由上至下分别为6和10，管的直径为20 cm。同样采用时域有限差分(Finite difference time domain， FDTD)法对该模型进行正演数值模拟，离散网格数量为600×360，网格大小为0.005 m×0.005 m。激励源采用中心频率为900 MHz的雷克子波，采样时窗为40 ns。天线收发间距为0.04 m，每0.02 m采集一道雷达数据，仿真得到的雷达剖面共有124道数据。

图4 管线仿真模型(a)和反射雷达剖面(b)Fig.4 Pipeline simulation model (a) and pipeline reflection radar profile (b)

仿真得到的GPR剖面图见图4b，由图4b可见较强的直达波信号、地面反射、管线的双曲线反射和地下介质分层处的反射。由于直达波信号较强，雷达剖面图中地下管线的反射信号较弱，不利于我们对地下目标特征分析，需要对数据进行去杂波信号处理。为了对比杂波抑制效果，分别使用减平均道法、奇异值分解法和背景矩阵减法三种算法对图4b数据进行处理，处理后的结果见图5。图5表明不同方法均能较好地去除直达波，但奇异分解法和减平均道法对最大振幅处杂波值计算存在偏差，进行杂波抑制时过度去除信号，导致雷达剖面中出现虚假信号(约6 ns和10 ns处)。但背景矩阵减法处理后效果最好，表现为其抑制结果更加干净，虚假信号(artefact)能量较低，尤其是6 ns左右的虚假信号。

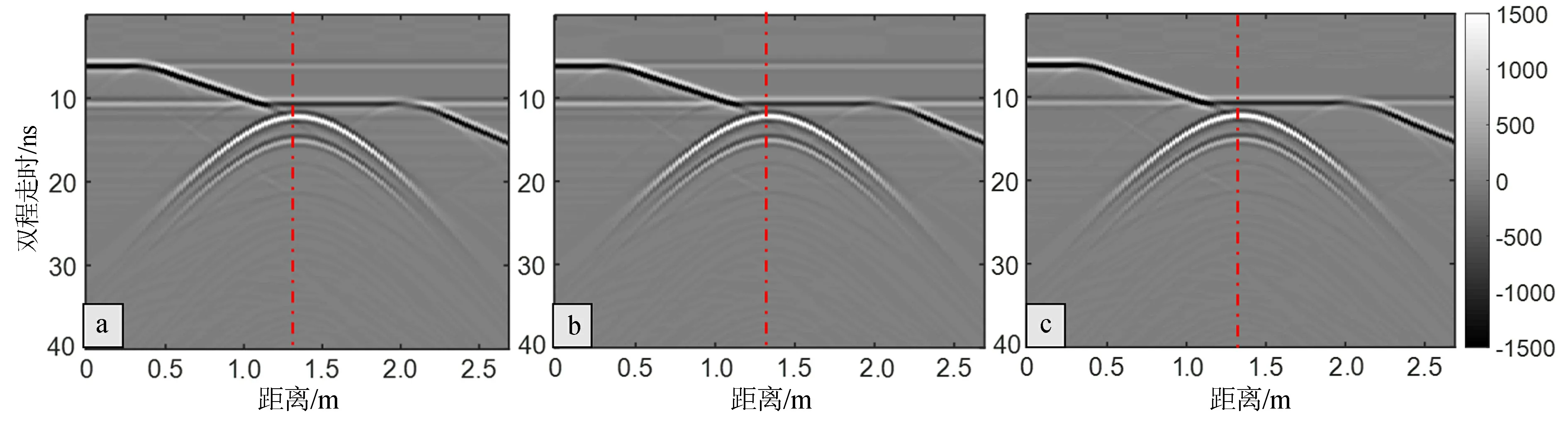
图5 杂波信号抑制后管线反射雷达剖面Fig.5 Pipeline reflection radar profile after clutter suppression(a)减平均道法(average trace subtraction) (b)奇异分解法(singular value decomposition) (c)背景矩阵减法(BMS)

为进一步对比不同方法的杂波抑制效果，从图5中提取出目标反射振幅，并通过计算处理前后振幅变化百分比来评估不同算法的优劣。选取图5红色虚线位置处目标反射单道信号，绘制目标反射信号的A-scan对比图(图6)。从图6中读取出目标反射振幅后发现三种算法处理后导致目标信号有所扰动，但对于背景矩阵减法处理后的目标信号振幅的衰减率0.5%远小于其他两种算法的衰减率5.4%。

图6 杂波抑制后管线单道反射信号Fig.6 Single channel reflectedion signal of pipeline after clutter suppression

3 现场试验

本节进一步对比分析了三种杂波去除方法在探地雷达实地数据处理中的效果。

3.1 钢筋混凝土结构探测

本小节对混凝土中钢筋探测数据进行了处理，数据采集使用意大利IDS公司生产的TRHF型号探地雷达，天线中心频率为2 GHz。测线水平距离约为0.7 m，共采集353道数据。采样时窗长度为8 ns，共512个采样点。

图7为混凝土中钢筋的雷达反射剖面(B-scan)，可以清晰地看到两根钢筋的双曲线反射信号以及地面杂波信号。采用前文介绍的三种杂波抑制算法进行处理，结果见图8。从图8中可以看到三种算法对杂波处理的效果相似，均能将直达波很好的去除，可以更加清晰地识别钢筋的双曲线反射。然而减平均道法(图8a)和奇异分解法(图8b)在处理后双曲线顶点附近产生虚假信号，这是因为算法本身的缺陷导致的。同样的，提取图8红色虚线位置的单道A-Scan，结果见图9。由图9可见，三种算法对直达波信号能够很好的去除，读取目标振幅后发现均存在一定衰减。但相较于其他两种算法，背景矩阵减法处理后对目标信号衰减值为原信号的31%，而减平均道和奇异分解法为原信号的39%，所以背景矩阵减法仍优于其他两种方法。

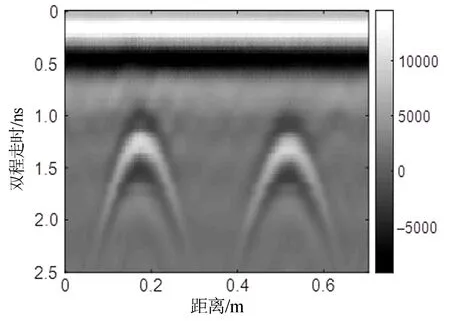
图7 钢筋反射雷达剖面Fig.7 Radar profile of rebar reflection

图9 杂波信号抑制后钢筋单道反射信号Fig.9 Single channel reflection signal of rebar after clutter suppression

3.2 地下管线探测

本小节对某地下管线的雷达探测数据进行了处理，试验采用意大利IDS探地雷达，选用中心频率400 MHz天线。测线长度约2.2 m，共采集92道数据，采样时窗长度为50 ns，采样点数为512个。

图10为实际采集的地下管线探地雷达剖面。由于有较强的直达波及不均匀背景介质引起的杂波，地下管线产生的双曲线型反射信号不能清楚呈现。采用前文介绍的三种杂波抑制算法分别对实测数据进行处理，处理后结果见图11。由图11可见三种算法对杂波处理的效果接近。直达波被很好地去除，直流成分也在一定程度上得到了去除，从而使管线的双曲线反射变得明显。但减平均道法(图11a)和奇异分解法(图11b)处理后的结果在目标双曲线顶点位置处存在虚假反射，这与前文仿真数据杂波抑制后的结果相似，而背景矩阵减法(图11c)没有出现虚假反射。同样绘制图11红色虚线位置处不同算法处理后管线目标单道信号，见图12，读取目标振幅后，计算出减平均道法、奇异分解法、背景矩阵减法三种算法处理后相对原始数据振幅百分比分别为120%，123%，139%。结果表明背景矩阵减法优于其余两种方法。

图10 管线反射雷达剖面Fig.10 Pipeline reflection radar profil

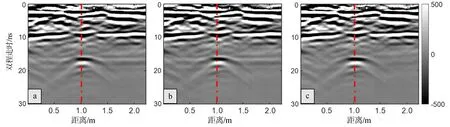
图11 杂波信号抑制后管线反射雷达剖面Fig.11 Radar profile of pipeline reflection after clutter suppression(a)减平均道法(average trace subtraction) (b)奇异分解法(singular value decomposition) (c)背景矩阵减法(BMS)