透彻理解知识内容 赢得二轮备考复习

山东 王 丽 刘焕芝

高考二轮复习的重要目的是在透彻理解知识点的基础上对已有知识应用的提升和飞跃。为了达到这个目的，建议二轮复习初始阶段先进行小题透练，再进行知识的拓展与提升。下面通过对力学中典型的瞬时作用问题和动态平衡问题进行小题透彻地剖析，希望能助力同学们二轮初期的备考。

一、品味瞬时作用小题，透彻理解弹力

受力分析贯穿整个高中物理，透彻理解各种力的特点是受力分析的基础和关键。分析比较下列两种典型情景中瞬时作用过程中弹力的变化，透彻理解弹力，同时体验应用牛顿第二定律解决动力学问题的思路。(设小球的质量为m)

情形1 如图1所示，剪断弹簧和剪断绳子瞬间，球的加速度分别是多少？剪断弹簧前后瞬间，绳上弹力分别为多少？

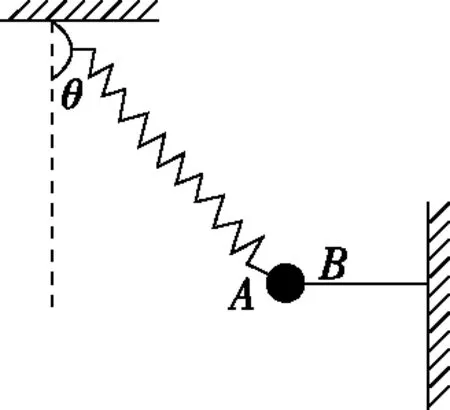
图1

情形2 如图2所示，剪断水平绳瞬间，球的加速度是多少？剪断水平绳前后瞬间，倾斜绳弹力分别为多少？

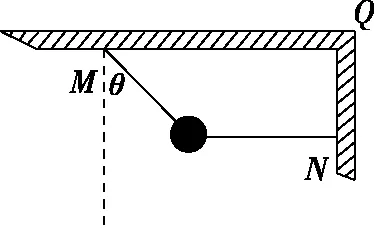
图2

【思路分析】加速度是联系运动和力的桥梁，求解加速度有两个角度分别为受力分析由牛顿第二定律求解和运动分析由运动学公式求解。若已知力的信息或未知运动的信息，则由牛顿第二定律来求解，若已知运动的信息但未知力的信息，则由运动学公式求解。

情形1解法 图1中剪断弹簧后，绳的拉力可能突变，故力的信息未知，可从运动的角度切入。

分析可知，剪断弹簧之后，球会做圆周运动。剪断弹簧瞬间，球做圆周运动的速度为零。受力分析如图3所示，由牛顿第二定律可知

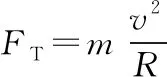
y轴方向有mg=ma

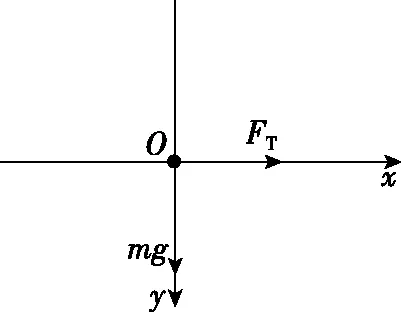
图3

解得FT=0，a=g，方向竖直向下，即剪断弹簧瞬间，球的加速度大小为g，方向竖直向下，绳上弹力为零。

剪断弹簧前，物体处于平衡状态时，由平衡条件得力的矢量三角形如图4所示

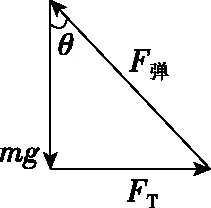
图4

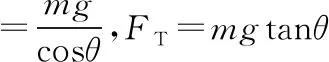
剪断绳前后，球受重力和弹簧弹力不发生变化，

合力为F合=mgtanθ，方向水平向左

【方法点拨】

(1)瞬时作用问题实质就是动力学问题，解题的根本思路是受力分析和运动分析，然后由牛顿第二定律和运动学公式求解，过程中需要理解弹力的特点，把握弹力的变化；

(2)不同情境下弹力特点及对应解决方法：若瞬时变化后剩下的是不能发生突变(弹簧、橡皮筋、弹性接触面等)的力，则瞬时变化前后，剩下的力不变，可根据变化前的状态求剩下的力及其合力，根据牛顿第二定律求加速度；若瞬时变化后剩下的是能发生突变(刚性绳、刚性杆、刚性接触面等)的力，应分析瞬时变化后物体的状态来确定变化瞬间加速度，然后再根据牛顿第二定律求加速度和可能变化的力；

(3)在弹性限度内，刚性物体的弹力可以发生突变，由运动来体现力的变化；而弹性物体的弹力由于形变量明显，弹力不会发生突变。

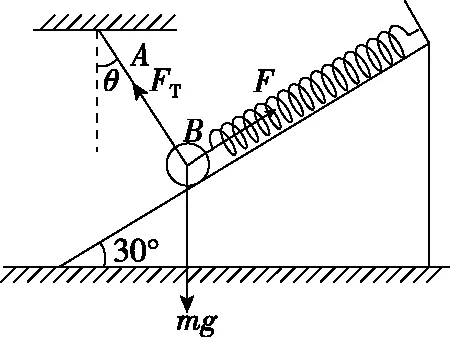
情形2解法 剪断水平绳瞬间，球做圆周运动，球的加速度垂直于倾斜绳，如图5甲所示，则

倾斜绳上的拉力F2=mgcosθ

甲

可见，剪断水平绳前后，倾斜绳上拉力发生了突变。

【方法点拨】水平绳剪断瞬间，物体将以悬点M为圆心做圆周运动，开始时刻速度为零，因此需要的向心力为零，即沿绳方向合力为零，所以F2=mgcosθ，倾斜绳上的拉力发生了突变。垂直于绳方向的力为小球所受合力，即F合=mgsinθ=ma。

【典例一】在倾角为30°的光滑斜面上有一质量为m的小球，小球分别与平行于斜面的轻弹簧和与竖直方向成θ=30°角的轻绳相连，如图6所示，此时小球处于静止状态，且斜面对小球的弹力恰好为零。则下列关于小球的加速度大小a的说法正确的是

( )

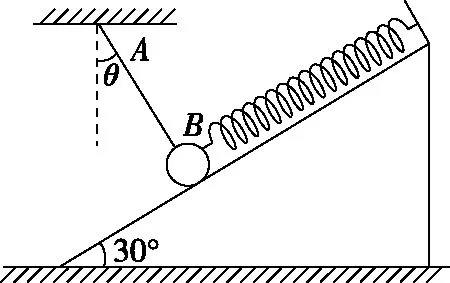
图6

A.剪断绳的瞬间，a=g

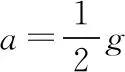
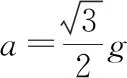
【解析】斜面对小球的弹力恰好为零，对小球进行受力分析如图7甲所示，小球处于静止状态，由平衡条件得力的矢量三角形如图7乙所示。

甲

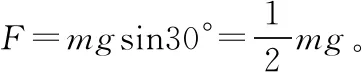
【方法点拨】本题关键是注意区分剪断轻绳和剪断弹簧的区别，剪断轻绳瞬间，轻绳的拉力消失，球有垂直斜面向下运动的趋势，斜面会给小球垂直斜面向上的支持力，使球仍保持静止。剪断弹簧瞬间，弹簧弹力消失，球做圆周运动，轻绳的拉力发生变化，斜面对球仍无作用力。根据牛顿第二定律确定加速度。

【典例二】A、B两球质量分别为m1和m2，用弹簧相连，长为l1的细线与A球相连，置于水平光滑桌面上，细线的另一端拴在竖直轴OO′上，如图8所示。当A球与B球均以角速度ω绕OO′在水平桌面上做匀速圆周运动，稳定后，弹簧长度为l2。求：

(1)此时细线的拉力大小；

(2)将细线突然烧断的瞬间，A球的加速度。

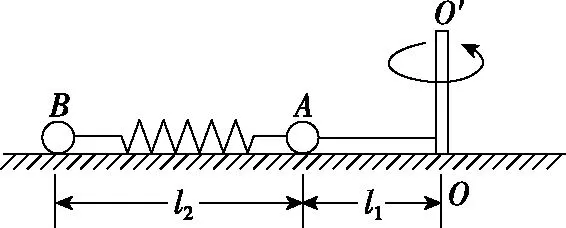
图8

【思路分析】

(1)B球绕OO′做匀速圆周运动，弹簧的弹力提供向心力，求出弹簧的弹力。A球在水平方向上受细线的拉力和弹簧的弹力，两个力的合力提供A球做圆周运动的向心力，从而求出细线的拉力。

(2)细线突然烧断的瞬间，细线拉力立即消失，弹簧的弹力来不及发生变化，根据牛顿第二定律求出A球的合力，从而得出A球的加速度。

【解析】(1)设弹簧的弹力为F，细线的拉力为FT，根据牛顿第二定律可知

对于A有FT-F=m1l1ω2①

对于B有F=m2(l1+l2)ω2②

解得FT=m2ω2(l1+l2)+m1ω2l1③

(2)细线烧断的瞬间，细线的拉力消失，弹簧形变未发生改变，A球所受合外力等于弹簧弹力

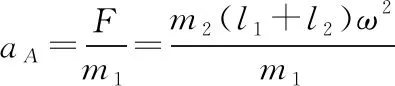
【方法点拨】动力学问题思考的方向是受力分析和运动分析，而解决本题的关键是知道匀速圆周运动的向心力由合力提供，知道在烧断细线的瞬间，拉力立即消失，弹簧弹力不变。

【方法总结】弹簧或弹性绳上弹力不能发生突变，若其他力发生突变后剩下弹簧或弹性绳的力，则通过分析突变前受力求瞬时加速度。刚性绳、刚性接触面上弹力可以根据需要发生突变，若其他力突变后剩下刚性绳或接触面的力，则通过分析突变后的运动情况求瞬时加速度。

二、品味三力动态平衡问题，悟矢量三角形灵活应用

物体在三个共点力作用下的动态平衡问题属于高中物理的主干知识，因其可以和三角形结合用图解法解决问题，可以很好地体现学生灵活应用知识解决问题的能力，也是高考的热点。图解法有时候只需分析力的动态三角形即可解决，有时候需借助情景条件，利用相似三角形才可解决，有时候需借助几何图形特点才可准确表达各力的关系，究竟什么时候利用动态三角形、什么时候借助相似三角形、什么时候借助其他几何图形特点？详见下面例题。

【典例一】在光滑墙壁上用网兜把足球挂在A点，足球与墙壁的接触点为B(如图9)。足球的质量为m，悬绳与墙壁的夹角为α，网兜的质量不计。从网兜的承受力上分析，绳长点好还是短点好？

图9

【思路分析】建模：从网兜承受力方向分析绳的长短，绳的长短改变绳与竖直方向夹角α的大小，即分析绳上拉力FA与夹角α的关系；

思路：对足球受力分析，建立各力和夹角之间的关系；

知识储备：物体平衡条件的具体表达形式；

足球受三个力作用，三个力的平衡条件用闭合三角形法表达最方便，即将各力平移首尾相接构成闭合三角形，三角形的边角代表力的大小和方向，通过分析三角形的边角变化来分析力的变化，进而解决问题。

【解析】对足球受力分析，当绳与竖直方向夹角为某一值时，由平衡条件得力的矢量三角形如图10所示，由图10可以看出，α角变化时，代表重力的竖直边长度和方向不变，代表墙壁支持力的水平边方向不变，三角形始终闭合，则绳越长，α角越小，FB越小，FA越小，因此绳子越长越好。

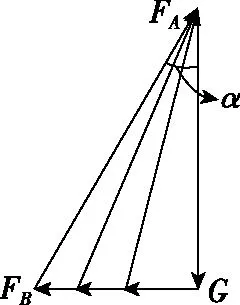
图10

【典例二】如图11所示，光滑的半球形物体固定在水平地面上，球心正上方有一光滑的小滑轮，轻绳的一端系一小球，靠在半球上的A点，另一端绕过定滑轮后用力拉住，使小球静止。现缓慢拉动轻绳，在小球沿球面由A移动到半球的顶点B的过程中，半球对小球的支持力FN和绳对小球的拉力FT的变化情况是

( )

A.FN变大

B.FN不变

C.FT变小

D.FT先变小后变大

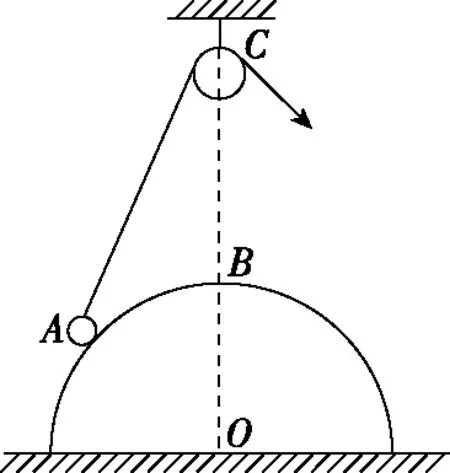
图11

【思路分析】该题中小球受三个力，想到通过分析动态三角形来分析力的变化，但分析过程中发现，代表重力的边大小方向不变，支持力和绳的拉力方向都在变化，结合题意情景，支持力方向始终沿OA方向，绳的拉力始终沿AC方向，力的三角形始终与△AOC相似，对应边成比例。

【解析】对小球进行受力分析，重力G、半球的支持力FN和绳的拉力FT构成矢量三角形如图12所示，

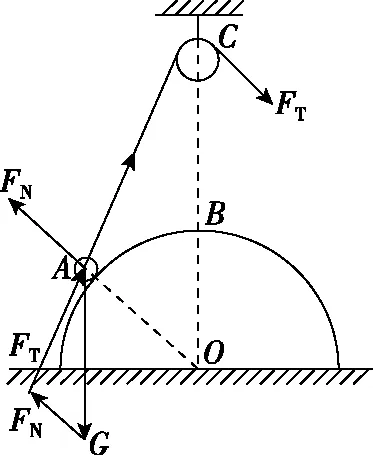
图12

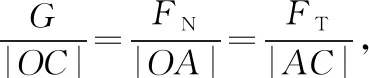
【方法点拨】因为力的矢量三角形有两个力方向都在变化，仅靠分析力的三角形变化无法确定代表力的两个边长的变化，需要再结合情景约束。观察该情景变化过程中力的三角形与情景的三角形始终相似，问题得以解决。

( )

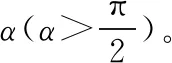
A.MN上的张力逐渐增大

B.MN上的张力先增大后减小

C.OM上的张力逐渐增大

D.OM上的张力先增大后减小

图13

【思路分析】该题重物共受到三个力，分析重物缓慢拉起过程中，OM、MN上的力方向变化，自然想到分析动态三角形，但直接分析动态三角形，发现由于保持α角不变的条件不好把握，而难以看出三角形两个边长的变化。联想到圆周角不变的数学工具，利用圆来约束α角不变，问题变得方便直观。

【解析】由于三力平衡合力始终为零，且α角保持不变，重力G保持不变，在圆周里画出这三个力动态平衡的矢量三角形，如图14所示，由图像可看出在OM由竖直被拉到水平的过程中，FOM先增大后减小，FMN一直增大。AD选项正确。

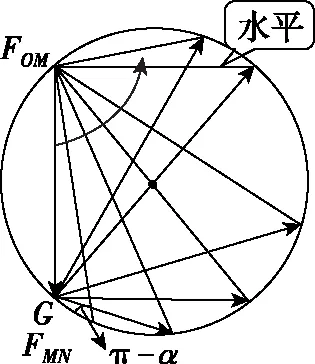
图14

【方法迁移】

1.若在OM由竖直被缓慢拉到水平后继续缓慢上拉，MN和OM上的力会再怎么变化？

由图14不难发现，OM缓慢拉到水平后继续缓慢上拉，MN和OM上的力都继续减小。

2.若α保持90°不变，在OM由竖直被缓慢拉到水平的过程中，MN和OM上的力会怎么变化？

α保持90°不变，代表重力的边应该是直径，如图15所示，可以得出MN上力增大、OM上的力减小。

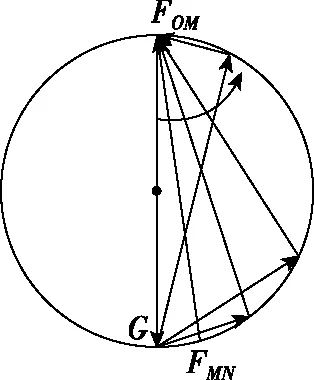
图15

3.轻绳两端固定在AB两点，中间O点系一重物，如图16现将杆顺时缓慢针转动，使OA从初始位置转到竖直位置，这一过程中OA绳的张力与OB绳的张力如何变化？

图16

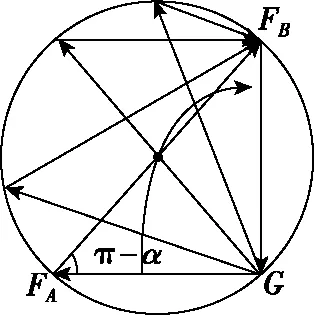
图17

如图17所示，FA先增大后减小，FB一直减小。

【方法点拨】该题因为力的矢量三角形有两个力方向都在变化，而且两个力方向夹角保持不变，在分析动态三角形中因夹角不变的条件无法准确体现，而借用圆周角不变来准确表示两个力夹角不变的条件，使问题得以解决。

【总结】用图解法分析三力的动态平衡问题时

1.一个力的大小方向均不变，第二个力的方向不变，第三个力的大小方向均变化时，直接根据力的矢量三角形建立各力的关系和变化方向，即可确定两个变力的大小的变化情况；

2.一个力的大小方向均不变，另两个力方向均变化，直接根据力的矢量三角形不方便找两个变力的大小变化规律，结合题意，借助情景约束或数学工具配合力的矢量三角形来解决问题；

3.这类问题最根本的依据是平衡条件的矢量三角形，究竟是否需借助相似三角形或其他几何工具，要根据解决问题的需要，不能死记或生搬硬套，要具体问题具体分析。

通过瞬时作用问题和平衡中的动态分析法的解析，希望能够引导大家注意，学习物理的过程，要注重领悟知识和方法的来龙去脉，因果关系。做到知其然知其所以然，才能融会贯通、灵活应用，切忌死记硬背、生搬硬套。