例谈匀变速直线运动问题中平均速度公式的运用

浙江 沈 卫

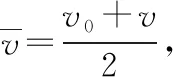
一、匀变速直线运动的实例分析

1.从运动学的基本规律出发解决问题

【例1】如图1所示，物体静止在水平地面上，某时刻给它施加一个水平方向的恒力F，使其在水平地面上做匀加速直线运动。可知物体在运动过程中第5个7 s内的位移与第11个3 s内的位移大小之比为

( )

A.2∶1 B.1∶2 C.7∶3 D.3∶7

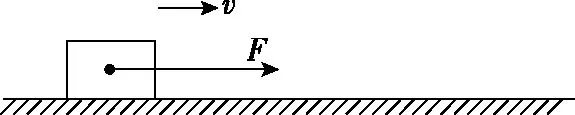
图1

【分析】物体由静止开始做匀加速直线运动，v1为第5个7 s初的瞬时速度，也是第4个7 s末的瞬时速度，速度大小满足v1=a·4t1=28a，因此第5个7 s内的位移x1大小满足：

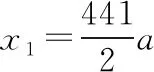
同理，第11个3 s内的位移x2大小满足：

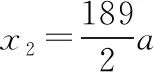
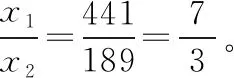
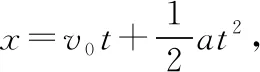
2.由基本规律的递推关系出发解决问题——运用逐差法计算位移

设第5个7 s内的位移为x5，第1个7 s内的位移为x1，因此有：

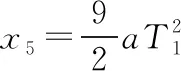
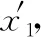
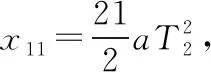
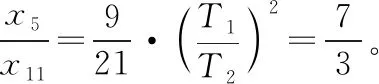
拓展问题已有的解法既是优化答题思路与途径的重要手段，也是帮助学生拓展知识面、锻炼思维的重要方式，更是帮助学生在解决问题中树立信心，形成学习兴趣的重要精神来源。同时还能在诸多解法的对比应用中找出最优解法，从而加深对概念的认知、规律的理解、解法的运用。

3.运用平均速度公式得出位移的比值关系

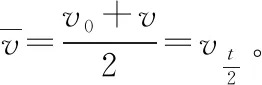
对比上述三种解法，可以看到平均速度公式在解决该问题中的优势。首先，平均速度公式的运用降低了计算量。平均速度公式依托其物理含义——中间时刻速度，轻易地解决了两个位移过程的速度关系，避免了平方项的计算；其次，运用平均速度公式确定了上述过程中位移大小之间的关系。任意过程中两个时间间隔内的位移关系也能够运用平均速度公式很快地予以确定。因此，教师在运动学模块的教学中，要重视平均速度公式的相关特点与运用，这将有助于学生对运动学模块的知识内容与应用产生更为全面的认识。

二、平均速度公式运用的实例分析

1.平均速度公式在复杂的匀变速直线运动问题中的运用

对于常见运动学问题的处理，往往需要在位移x、时间t、初速度v0、末速度v及加速度a这五个物理量已知三个或三个以上才能运用匀变速直线运动的基本规律进行处理，这是学生喜闻乐见的题型。但对于上述条件所给不完全的问题，该如何运用匀变速直线运动规律进行求解呢？

【例2】一个物体做匀加速直线运动，它在第3 s内的位移为5 m，下列说法正确的是

( )

A.物体在第3 s末的速度一定是6 m/s

B.物体的加速度一定是2 m/s2

C.物体在前5 s内的位移一定是25 m

D.物体在第5 s内的位移一定是9 m

【分析】上述条件会使学生产生一个错觉，前5 s内物体在每1 s的位移满足1∶3∶5∶7∶9，则第1 s内的位移为1 m，第5 s内的位移为9 m。因此，四个选项都是正确的，答案即为ABCD，显然，这对于选择题而言是不符合逻辑的。学生之所以有这样的错觉，是把物体运动看成初速度为零的匀加速直线运动，而题干并未说明，即物体运动的初速度可能为零也可能不为零，因此ABD选项错误。根据第3 s内位移为5 m可知，第3 s内的平均速度为5 m/s，即第3 s内的中间时刻速度为5 m/s，即前5 s内的中间时刻速度为5 m/s，即前5 s内的平均速度为5 m/s，因此前5 s内的位移一定是25 m，C选项正确。

【例3】做匀减速直线运动的物体4 s停止，若第1 s内的位移为14 m，则最后1 s内的位移是多少？

【分析】运用逆向思维，该问题很明显满足位移的比例关系，即第1 s内位移与最后1 s内位移比例关系满足7∶1，因此最后1 s内位移为2 m。

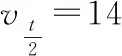
根据逆向思维，最后1 s内的位移为

如果例3中的问题变为物体经3.5 s停止，则在计算最后1 s内发生的位移大小时比例关系就不再不适用了，但平均速度公式仍可以使用。若物体经3.5 s停下，时间Δt=3 s，因此物体的加速度a满足

显然平均速度公式在该问题中的运用比位移的比例关系更具普适性，在解决问题中也更能突出问题中运动学的规律与本质。因此在教学活动中，教师适当地向学生传达平均速度公式的相关巧妙应用，可以帮助学生强化对运动学规律的认识与掌握，增加学生应对难题、解决难题的能力与信心。

2.平均速度公式在处理纸带数据中的运用

运用打点计时器与纸带探究匀变速直线运动的规律时，对于纸带上计数点瞬时速度的计算便是依据匀变速直线运动的平均速度公式。

【例4】某同学用打点计时器研究小车的匀变速直线运动，他将打点计时器接到频率为50 Hz的交流电源上，实验时得到一条纸带如图2所示。他在纸带上便于测量的地方选取第一个计数点A，之后每5个点取一个计数点。测量时发现B点已模糊不清，他只测得AC长为14.56 cm，CD长为11.15 cm，DE长为13.73 cm。请问，根据上述数据能否计算出AB的距离。

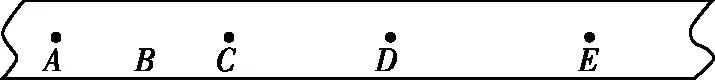
图2

【分析】虽然B点模糊不清，但是根据已有的数据分析运用逐差法可以得到纸带的加速度为

同理可知

xBC-xAB=aT2，其中T为相邻计数点间的时间间隔，T=0.1 s，因此xBC-xAB=0.0258 m=2.58 cm ①

同时AB的距离与BC的距离之和满足

xAB+xBC=14.56 cm ②

联立①②两式即可得到AB与BC的距离分别为

xAB=5.99 cm，xBC=8.57 cm

除了利用逐差法可以确定AB间的距离之外，还可以利用平均速度公式来进行处理。

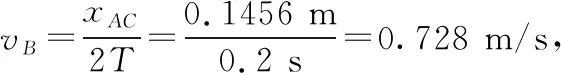
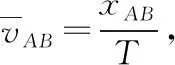
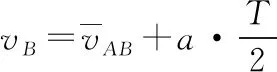
将数据代入表达式③即可求得xAB=5.99 cm

纸带出现点迹模糊的情况在力学实验中属于常见现象，如果运用运动学规律对模糊的点迹进行探讨，不仅可以确定模糊的点迹位置，引发学生的兴趣与思考，同时还可以深化匀变速直线运动规律在解决实际问题中的运用，加深学生对运动学公式及其变化的认识与理解。

匀变速直线运动规律是构成高中阶段物理知识体系的基本框架，是学生学习其他物理模块知识的必备基础，同时，平均速度公式也是最重要的知识内容之一。虽然其公式与定理内容并不多，但仔细分析会发现每一个规律与定理都有其独特的变化与运用。所以即便是简单的平均速度公式也有在解决具体问题中的多种表现与作用，不可小觑。因此，教师更要注重对基本概念与规律的深挖、深究，促使学生多思考、多探讨，从而充分发挥学生的学习能动性，提高学生的学习能力、思维能力与解决实际问题的能力。