立足科学思维 注重数学思想
——2020年全国高考理综卷Ⅰ第18题的一题多解
2021-04-08陕西成均武党维军
陕西 成均武 党维军
2020年全国高考理综卷Ⅰ第18题,考查带电粒子在有界匀强磁场中做圆周运动的临界极值问题。此类问题是高考的热点,也是考查学生科学思维及核心素养的重点题型。本文立足科学思维,根据带电粒子受洛伦兹力的特点,建立圆周运动模型,根据物理规律,科学推理转化极值问题,运用数学方法,科学论证极值条件。注重数理思想,运用分类讨论思想分析临界极值状态,通过几何图解法、函数极值法和焦点三角形法计算极值及其存在的条件。另外,通过尺规作图、特殊值法和排除法得出正确答案,形成了多种解题方法,充分体现应用数学思想方法解决物理问题的重要性。
一、真题呈现
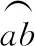
( )
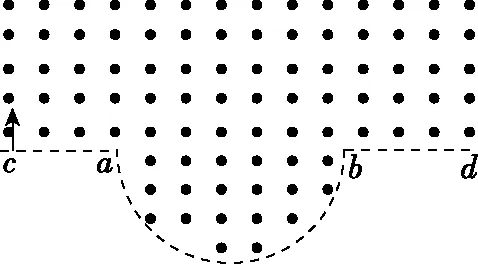
图1
二、审题与分析
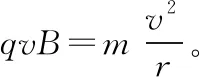
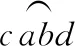
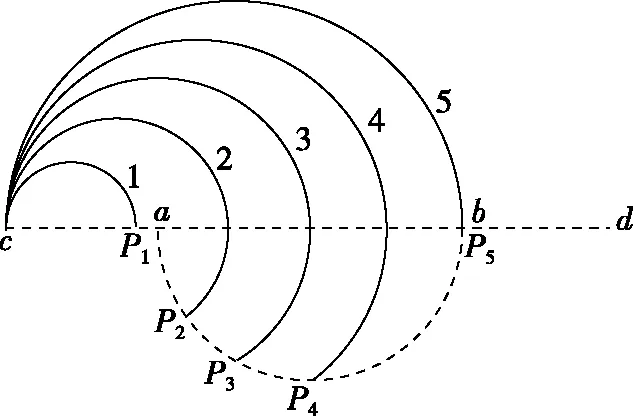
图2
三、最大圆心角的3种数学解法
解法1:几何图解法
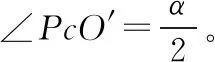
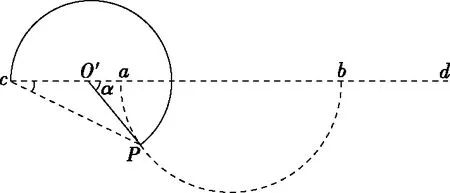
图3
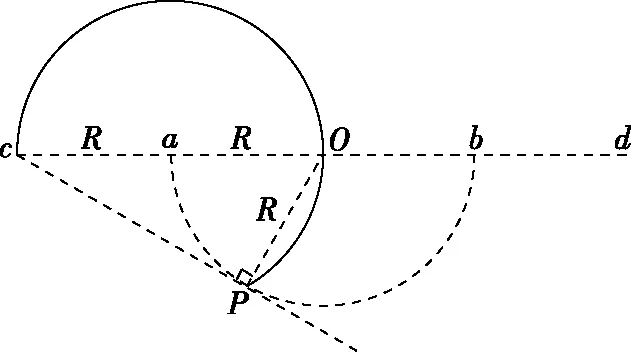
图4
【思路点拨】分析题意作图后,应考虑当粒子出射点在何处时,轨迹弧所对的圆心角有最大值。因直线cabd上方的轨迹弧恒为半圆,故半圆形区域内的轨迹弧所对的圆心角有最大值即可。最大值的确定需要运用同弧所对的圆周角等于圆心角的一半、圆的切线及直角三角形相关几何知识。几何图解法是本题最简捷的一种解题方法,但是需要学生具有较好的平面几何素养。
解法2:函数极值法
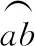
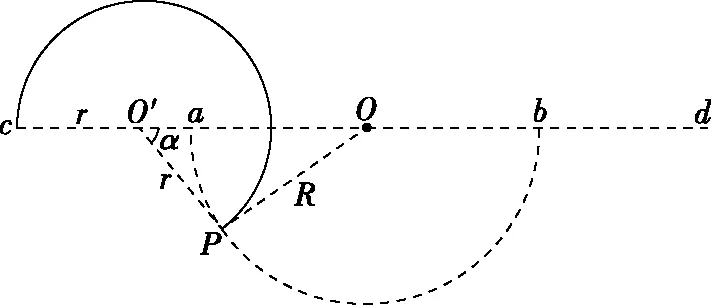
图5
根据几何关系有PO=R,PO′=r,O′O=2R-r,由余弦定理可知
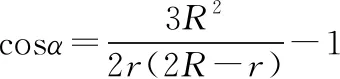
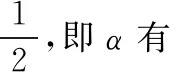
【思路点拨】作图分析题意后,不难发现磁场中轨迹弧的圆心角α随着轨迹半径r的变化而变化,根据余弦定理建立函数关系,整理函数表达式后再求函数极值。一般的临界极值问题都可以运用函数思想方法,确定自变量和因变量,建立函数关系解出函数表达式,运用数学方法分析取极值的条件,确定函数极值。运用函数思想方法求极值是比较严谨的一种方法,但是运算量较大、耗时较多,考试中可优先考虑其他方法,此方法可作为最后的保底方法。
解法3:焦点三角形法
如图6所示,△O′PO中,OP长度恒为R,O′O=2R-r,PO′=r,轨迹圆心O′到P点和O点的距离之和恒为2R。根据椭圆的第一定义:平面上到两定点距离之和等于常数的点的集合。所以,圆心O′始终在以P和O为焦点、长轴为2R的椭圆上,因点P不是定点会使椭圆位置变化,但其形状不变,不影响对α角的判断。
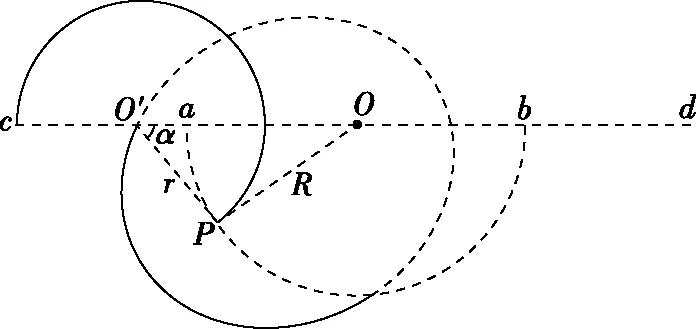
图6
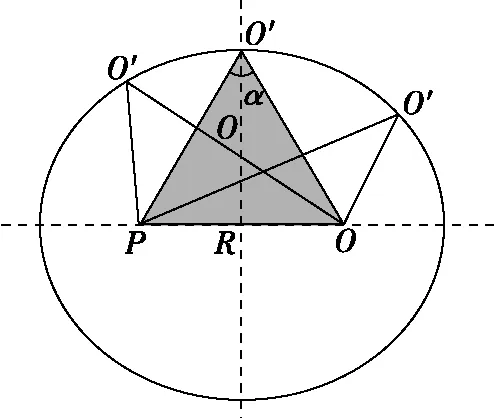
图7
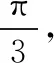
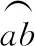
四、尺规作图排除法
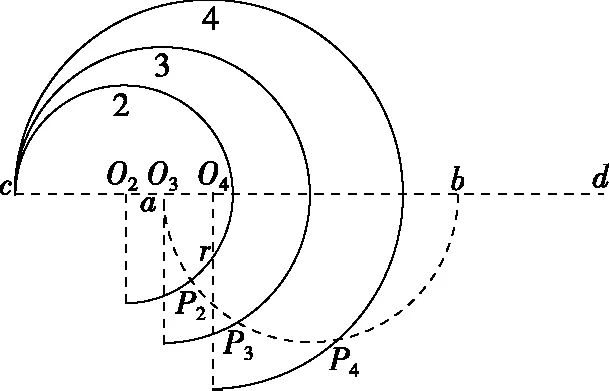
图8
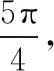
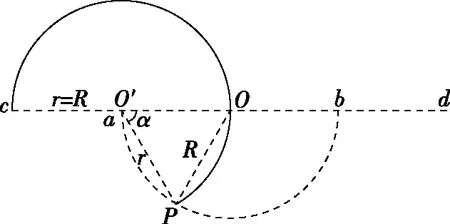
图9
【思路点拨】选择题审题不仅要阅读题干,观察配图,更要分析选项。分析选项有时能对解题带来提示,例如本题每个选项都对应一个角度,看似问最长的运动时间,实则求轨迹弧最大圆心角。D选项是四个备选答案中角度最大的一个,可先使用尺规作图法排除,A和B选项可用作图量角或特殊值法排除。规范作图的能力是学习物理必备的基本功,审题与解题时,规范地作图会有事半功倍的效果,临场考试中规范的尺规作图、角度测量与合理推断也可作为一种解题方法。
五、备考建议
带电粒子在有界匀强磁场中做圆周运动的临界极值问题,一直是考查科学思维的热点题型,对建立运动模型、科学推理、科学论证、几何作图、数理思想等能力素养有较高的要求。复习备考中要立足科学思维、注重数理结合思想,追求一题多解才能跳出题海。面对极值问题,运用物理规律科学推理转化问题是解题的重要环节;培养规范的尺规作图能力,储备常用的几何定理,判断几何关系、解决极值问题才能得心应手;临场考试中选择题审题时不忘分析选项,运用特殊值法、排除法等往往能快速得到正确答案。
