Structures and Stability of Th(N6), Pa(N6), and U(N6)
2021-04-08GAOYangLEIJiehong雷洁红
GAO Yang(高 扬), LEI Jiehong(雷洁红)
Physics and Space Science College, China West Normal University, Nanchong 637002, China
Abstract: The cyclo-N6 anion is a total nitrogen unit with higher nitrogen content than cyclo-. However, the low decomposition barrier of cyclo-N6 anions hinders its application as a high energy density material (HEDM). Using first-principles calculations, we reveal that the covalent components that enhance the interaction between the cyclo-N6 anion and the cation can effectively improve the stability of cyclo-N6 anions. The actinide metals (Th, Pa, U) are selected as suitable cations. Further electronic structure analysis showed that the charge transfer from the actinide metal to cyclo-N6 anions resulted in a strong covalent bond, which promoted the stability of the cyclo-N6 anion in the Th(N6), Pa(N6), and U(N6) structure. This discovery is helpful for the rational design and synthesis of new HEDMs.
Key words: cyclo-N6 anion; first-principles calculation; high energy density material (HEDM); environmental friendliness; density functional theory
Introduction
The discovery and synthesis of high energy density materials (HEDMs) has always been a hot spot in the field of military research[1]. Among them, nitrogen clusters are of great significance as HEDMs for propulsion and explosion, mainly due to the huge energy difference among the single, double and triple bonds of nitrogen, and the final decomposition products are not polluting the environment[2-5]. Although many theoretical studies predicted that the polymer phase of pure nitrogen may be stable, until cubic gauche (cg-N) is experimentally synthesized at high temperature and high pressure, and it is metastable when restored to room temperature and the pressure is above 42 GPa[6-8]. Therefore, the pursuit of a nitrogen cluster compound with high energy and sufficient stability has been facing great challenges.

In this paper, we report a metal compound Th(N6), Pa(N6), and U(N6) containing cyclo-N6anions. Theoretical analysis from different angles shows that the series of structures exist stably under ambient conditions.
1 Computation Details
All structures were performed on the M06-2X level under the third-generation empirical dispersion-corrected density functional theory (DFT-D3)[28], which had certain advantages in calculating the interaction between molecules[29-30]. For actinide metals, the (14s13p10d8f6g)/[10s9p5d4f3g] valance basis set with small-core relativistic effective core potentials (RECP)[31](including 60 core-electrons) was selected, but N was used d-polarized double ζ valence electrons 6-31G*[32]basis set. In addition, the vibration frequency of all structures was also performed at the same level to ensure the reliability of the structure. All calculations were performed using Gaussian 09 software package[33].
In order to understand the stability of the structure, a series of electronic structure analysis were performed, including charge transfer and energy decomposition analysis (EDA). In addition, the contribution of cyclo-N6to molecular orbitals could be visually revealed through the total density of states (TDOS) and partial density of states (PDOS) diagrams. In order to better understand the interaction between actinide metals and cyclo-N6anions, the Amsterdam Density Functional (ADF) program[34]was used for EDA, and Multiwfn[35]was used for other electronic structure analysis.
2 Results and Discussion
By optimizing different initial structures, we have obtained the metal compound Th(N6), Pa(N6), and U(N6) that combines actinides with cyclo-N6anions. As shown in Fig. 1, the actinide metal forms six coordination bonds with the nitrogen in the cyclo-N6anion. The different spin multiplicity of the Th(N6), Pa(N6), and U(N6) structure is calculated. The ground state is determined by the lowest total bond energy. The ground states of Th(N6), Pa(N6) and U(N6) are singlet state, doublet state and triplet state, respectively. By counting the average bond length between the actinide metal and the cyclo-N6anion, we find that as the atomic radius of the actinide metal decreases, the average bond length between the actinide metal and cyclo-N6anions also gradually decreases, and it is 0.226, 0.224 and 0.223 nm. In addition, the atomization energy and bond energy of the Th(N6), Pa(N6), and U(N6) structure are also counted. Among them, the atomization energy and total bond energy of the U(N6) structure are the largest, which are respectively 48.32 eV and -34.99 eV. The Th(N6) structure is the second, and Pa(N6) is the smallest. It shows that the bond between U and cyclo-N6anions is the least easy to break, and the U(N6) structure is the most stable one. Moreover, Wiberg bond and Mayer bond orders between actinide metal and N are counted (Table 1), and the value is close to 1, indicating the formation of a single bond between actinide metal-N, which is consistent with the results in Fig. 1.

Fig. 1 Geometric structure diagram of (a) ThN6;(b) PaN6; (c) UN6

Table 1 Average bond order analysis among Th-N, Pa-N and U-N
To realize the nature of Th(N6), Pa(N6), and U(N6), we start from the energy perspective. The energy decomposition analysis between the two fragments of actinide metal and cyclo-N6anions are shown in Fig. 2, where Eorb, Eelecand Edisrepresent the attraction terms of the intermolecular interaction of Th(N6), Pa(N6), and U(N6) contribution. The green Eorbrepresents the ratio of the orbital term to the total attractive term, and the pink Eelecrepresents the ratio of the electrostatic term to the total attractive term. Since the dispersion term Edisaccounts for a very small percentage of the total attraction term, thus it is ignored. As shown in Fig. 2, it can be seen that the proportion of orbital terms of all structures (greater than 70%) is much greater than that of electrostatic terms (less than 30%), indicating that the overlapping wave function between the two segments is dominant. The actinide metal and cyclo-N6anions are connected by strong covalent bonds.
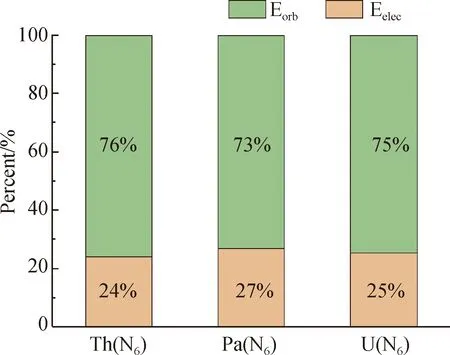
Fig. 2 Energy decomposition analysis of Th(N6),Pa(N6), and U(N6) structures
In order to understand the stabilization mechanism of cyclo-N6anions in Th(N6), Pa(N6) and U(N6) structure, we perform Mulliken, Hirsheld and voronoi deformation density (VDD) charge calculations (Table 2). From the statistical results of three different charges, it can be seen that the actinide metals (Th, Pa, U) are approximately positive charged, and the cyclo-N6anion is negatively charged. It is worth noting that the actinide metal transfers all the charges to cyclo-N6anions, indicating that the charge transfer between the actinide metal and cyclo-N6anions enhances the cyclo-N6anion stability in the Th(N6), Pa(N6) and U(N6) structure. By comparing the three structures, we found that the Mulliken and Hirsheld charges of the Th(N6), Pa(N6) and U(N6) structure have certain rules, the cyclo-N6anion in Pa(N6) has more negative charges, followed by U(N6) and the least Th(N6). This also explains the stronger electrostatic interaction between Pa and the cyclo-N6anion in the PaN6structure, as shown in Fig. 2. In addition, the N-N bond in the cyclo-N6anion is a covalent bond and is stabilized by transferring electrons from actinide metals.
In order to further confirm this conclusion, we analyze the PDOS of Th(N6), Pa(N6) and U(N6) structure, as shown in Fig. 3. The black line and colored lines represent TDOS and PDOS, respectively. The isovalue of the molecular orbital diagram is 0.03. In the energy range below the highest occupied molecular orbital (HOMO), the energy band of the cyclo-N6anion plays a leading role. In particular, at the position of HOMO in Fig. 3(a), we find that the energy band of the cyclo-N6anion is almost close to the TDOS, while the energy band of Th is almost zero. This result shows that the orbital hybridization between Th and cyclo-N6anions is eliminated and replaced by charge transfer, resulting in a strong ionic bond interaction between Th and cyclo-N6anions in the Th(N6) structure[20, 36]. At this time, the high occupied molecular orbital-lowest unoccupied molecular orbital (HOMO-LUMO) gap in the Th(N6) structure is 4.39 eV. For the open-shell Pa(N6) and U(N6) structures[Figs. 3(b)-(c)] at the HOMO position of α molecular orbital, the energy band between the metal and cyclo-N6anions is very close. However, it is at the HOMO position of β molecular orbital, the energy band of the cyclo-N6anion is dominant. Combining the energy band changes of the two molecular orbitals, the metal and cyclo-N6anions are connected by strong ionic bond interaction. Therefore, these results confirm the stable existence of cyclo-N6anions in Th(N6), Pa(N6) and U(N6) structure.

Table 2 Mulliken, Hirsheld and VDD charge values of actinide metals and cyclo-N6 anions in Th(N6), Pa(N6), and U(N6) structure

Fig. 3 PDOS of (a) Th(N6); (b) Pa(N6); (c) U(N6)
3 Conclusions
In summary, we applied first-principles calculations to report a stable Th(N6), Pa(N6), and U(N6) structure. The stability of structures is proved by the analysis of the electronic structure from different perspectives. The energy decomposition results show that the actinide metal and cyclo-N6anions are connected by strong covalent bonds, and the charge transfer and the PDOS reveal that the strong covalent bond between actinide metal and cyclo-N6anions is the stability of cyclo-N6anions. It is expected to solve the problem of low decomposition barrier of cyclo-N6anions, and making it become a potential HEDM. In addition, through simple calculations, the atomization energy and the bond energy of U(N6) structure are both the largest, and thus U(N6) structure is the most stable.
杂志排行
Journal of Donghua University(English Edition)的其它文章
- Effect of Blending Ratio on Properties of Core Yarn and Fabric of Polysulfonamide (PSA)/Flame Retardant Viscose (FRV)/Conductive Filament
- Tensile and Electro-Mechanical Properties of Carbon Nanotube Film Twisted Yarn with Adjustable Diameter
- Metaphor Analysis Method Based on Latent Semantic Analysis
- Structural Reliability Analysis Based on Support Vector Machine and Dual Neural Network Direct Integration Method
- Implicit Attribute Recognition of Online Clothing Reviews Based on Bidirectional Gated Recurrent Unit-Conditional Random Fields
- Mechanical Properties of Glass Fiber/Unsaturated Polyester Resin Composite Water Collector
