基于GA-BP神经网络的变压器绕组热点温度预测研究

王兴桐，邹 宇，喻彩云

(1.三峡大学电气与新能源学院，湖北 宜昌 443002；2.广西电网钦州供电局，广西 钦州 535000)

随着国民经济的高速发展，保障电网的安全可靠运行显得越来越重要，变压器是电力系统核心设备之一，其使用寿命受绝缘性能的影响很大。变压器绕组热点温度是电力变压器绕组绝缘关键影响因素，同时也是衡量变压器负载能力的重要指标[1]，因此，研究一种变压器绕组热点预测方法，及时准确地获取变压器绕组热点温度，对保证变压器高效、安全、可靠运行具有重要意义。

目前，变压器绕组热点温度获取的方法有直接测量、模型计算和预测拟合3种[2]。直接测量法是由变压器内部温度传感器测量其内部温度，受传感器安装位置的影响较大。模型计算法是根据绕组热点温度通用规范来计算变压器内部温度，一般采用IEEEC57.91和IEC354导则[3-4]，但没有考虑环境温度的影响。随着智能算法的兴起，神经网络、支持向量机和卡尔曼滤波等预测算法被应用到绕组热点温度预测领域[5-7]。文献[8]利用油浸式变压器的油流动状态建立流体网络模型，计算得到变压器内部的温度分布，该方法虽然大大减少了计算量，但忽略了环境温度影响。文献[9]为了实现电力变压器绕组热点温度的实时预测，把负载电流、顶层油温、环境温度等3个因素作为特征向量，采用改进后的网格搜索算法对支持向量的参数进行优化，提出了一种变压器热点温度预测方法，但该方法的预测精度有待进一步提高。文献[10]采用容错度高、鲁棒性好的广义回归神经网络进行变压器绕组热点温度预测，取得较好的应用效果，但神经网络容易陷入局部最优，该方法有待进一步改进。

针对上述预测方法中存在的不足，本文采用遗传算法对BP神经网络的权值和阈值进行优化，克服了BP神经网络容易陷入局部最小值的缺陷，加快了算法的收敛速度，建立基于遗传算法优化BP神经网络的变压器绕组热点温度预测模型，采用实际算例验证该方法的有效性和通用性。

1 BP神经网络

1.1 BP神经网络原理

BP神经网络是学者Rumelhart提出来的，是一种需要经过多次前向传播的网络。其特点是信号由输入端传到输出端，而误差是由输出端传向输入端[11]。BP神经网络结构分为3层：输入层、隐含层和输出层，其结构如图1所示。

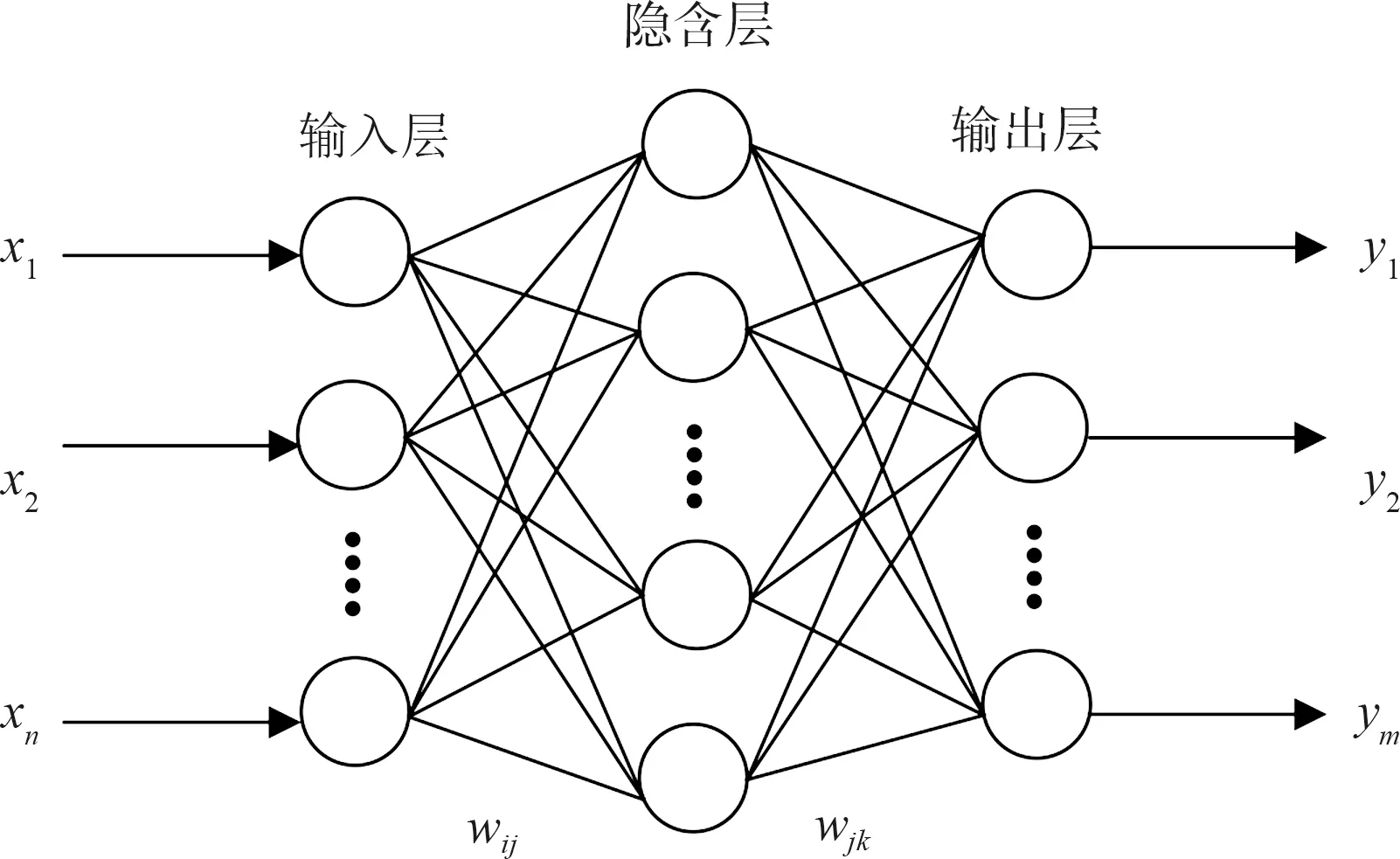
图1 BP神经网络结构

BP神经网络原理：设x1、x2、L、xn为神经元的输入量，y1、y2、L、ym为神经元的输出量，输入层神经元数量为n，隐含层神经元数量为l，输出层神经元数量为m，信号正向传播时，隐含层第j个神经元输入的加权和为

(1)

式中：wij为输入层第i个神经元与隐含层第j个神经元之间的连接权值；ai为隐含层阈值，i=1、2、L、n。

对于隐藏层的神经元，其激发函数可以写为

(2)

则隐含层第j个神经元为

(3)

式中：j=1、2、L、l。

将输出层的阈值记作bk，同理，输出层中第k个神经元的输入为

(4)

式中：wik为隐含层第i个神经元与输出层第j个神经元之间的连接权值；bk为输出层阈值，k=1、2、L、m。

反向传播时即为误差传递的过程，通过计算神经元的误差，不断修正权值和阈值。令Yk为输出层的第k个神经元输出值的期望，则第k个神经元的输出误差为

ek=Yk-Ok

(5)

式中：ek为输出误差。

a.权值的修正

输出层权值可用式(6)进行修正，公式为

(6)

式中：Δwik为输出层的权值修正量，i=1、2、L、l；j=1、2、L、m。

隐含层权值修正公式为

(7)

式中：Δwij为隐含层的权值修正量，i=1、2、L、n；j=1、2、L、l。

b.阈值的修正

隐含层阈值可采用式(8)进行修正，公式为

(8)

式中：Δai为隐含层阈值修正量，j=1、2、L、l。

输出层阈值的修正公式为

Δbj=ek

(9)

式中：Δbj为输出层阈值修正量，k=1、2、L、m。

1.2 BP神经网络的主要缺陷

首先，BP神经网络的应用效果受其权值和阈值初始值的影响很大，因此神经网络正向传播时，容易陷入局部极小值，影响预测效果。

其次，BP神经网络采用的是梯度下降法，导致 BP神经网络在对复杂目标函数进行优化时，所需训练时间过长，导致算法的迭代次数过多且收敛较慢。

基于上述两种原因，本文采用遗传(GA)算法对BP神经网络的权值和阈值进行优化，形成新的GA-BP神经网络算法，并将其应用于变压器绕组热点温度分析计算。

2 GA-BP神经网络预测模型

遗传算法是一种基于生物遗传寻优算法，通过迭代计算筛选并保存适应度函数中的优良个体，这种方法既能保存母体信息，又能使个体得到优化，如此反复遗传迭代直至找出最优个体，因其具有非常强大的全局寻优能力，常被应用于神经网络等智能算法的参数寻优[12]。

GA-BP神经网络计算过程主要包括BP神经网络结构参数的确定、GA优化BP的权值和阈值、BP预测输出等3个部分。GA-BP神经网络算法流程如图2所示。

图2 GA-BP神经网络算法流程

a.计算适应度函数

利用BP神经网络计算种群样本的权值和阈值，记期望输出为y，预测输出为o，则个体适应度为

(10)

式中：m为输出层神经元个数；yi为第i个期望值；oi为第i个预测值。

b.选择运算

根据个体适应度，选择优良个体遗传给下一代，本文采用的计算方法是轮盘赌法。

fi=k/Fi

(11)

(12)

式中：fi为个体i的适应度；Fi为个体i的适应度函数；k为选择系数；pi为个体i的选择概率。

c.交叉运算

GA算法在计算过程中采用实体编码，本文采用实数交叉法。

axi=axi(1-b)+ayib

(13)

ayi=ayi(1-b)+axib

(14)

式中：axi为第x个染色体的i位；ayi为第y个染色体的i位；b为随机数，0≤b≤1。

d.变异运算

选中某一个体后，把某些基因以某一概率转化为其他等位基因。

(15)

(16)

式中：amax为基因aij的上界；amin为基因aij的下界；r2为随机数；g为迭代次数；Gmax为最大迭代次数；r为随机数，0≤r≤1。

3 算例分析

本文采用文献[13]中500组变压器绕组热点温度试验数据组成样本进行算例分析，该样本数据是在连续时间序列上记录的数据，时间间隔是30 min，记录的数据包括变压器负载电流、顶层油温、底层油温、油箱上死角与油箱下死角温度、环境温度以及绕组热点温度，部分数据如表1所示。

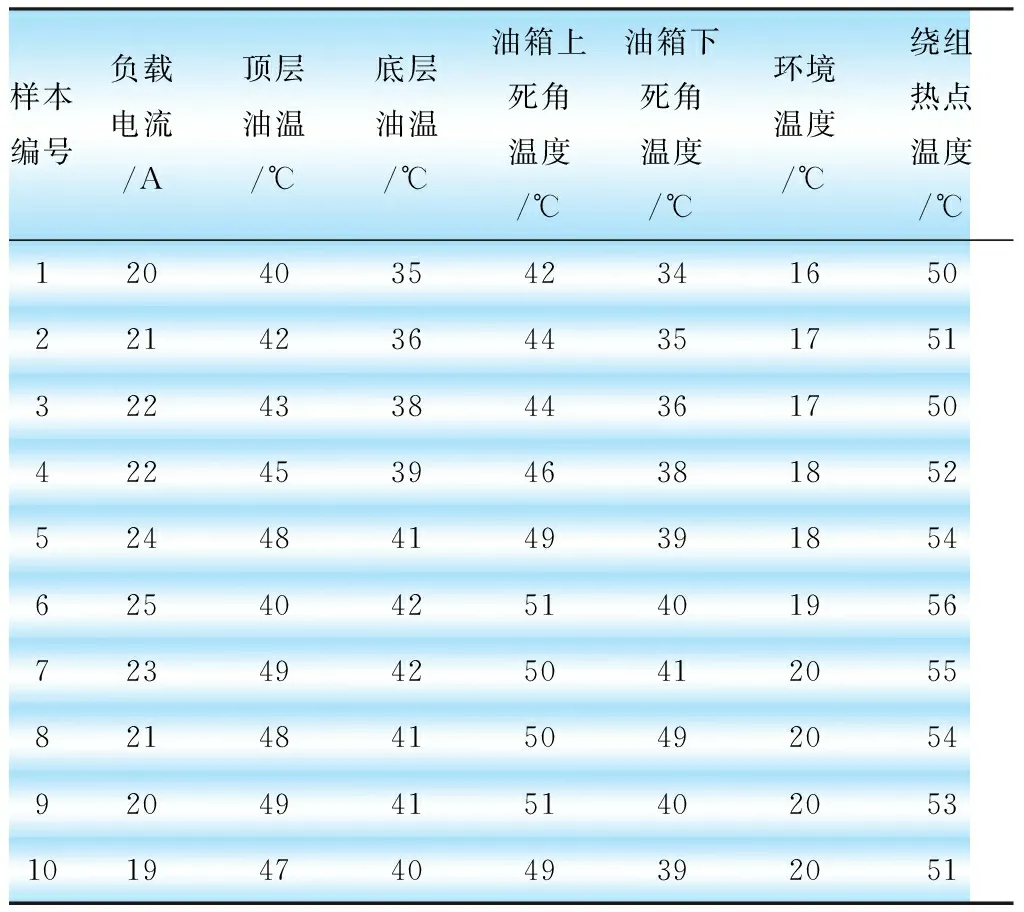
表1 部分样本数据

在Matlab2012b软件中进行仿真，GA-BP神经网络的参数设置如下：遗传算法的种群规模为30，交叉概率为0.4，变异概率为0.2，最大迭代次数为200；输入层神经元个数n=6，隐含层神经元个数l=9，输出层神经元个数m=1。本文将样本数据分为两部分，前450组数据作为训练集用于训练模型，后50组作为预测集用于检验预测模型的精度。采用训练集数据对GA-BP神经网络预测模型进行训练后，对测试集数据进行预测，预测结果如图3所示，绝对误差如图4所示。

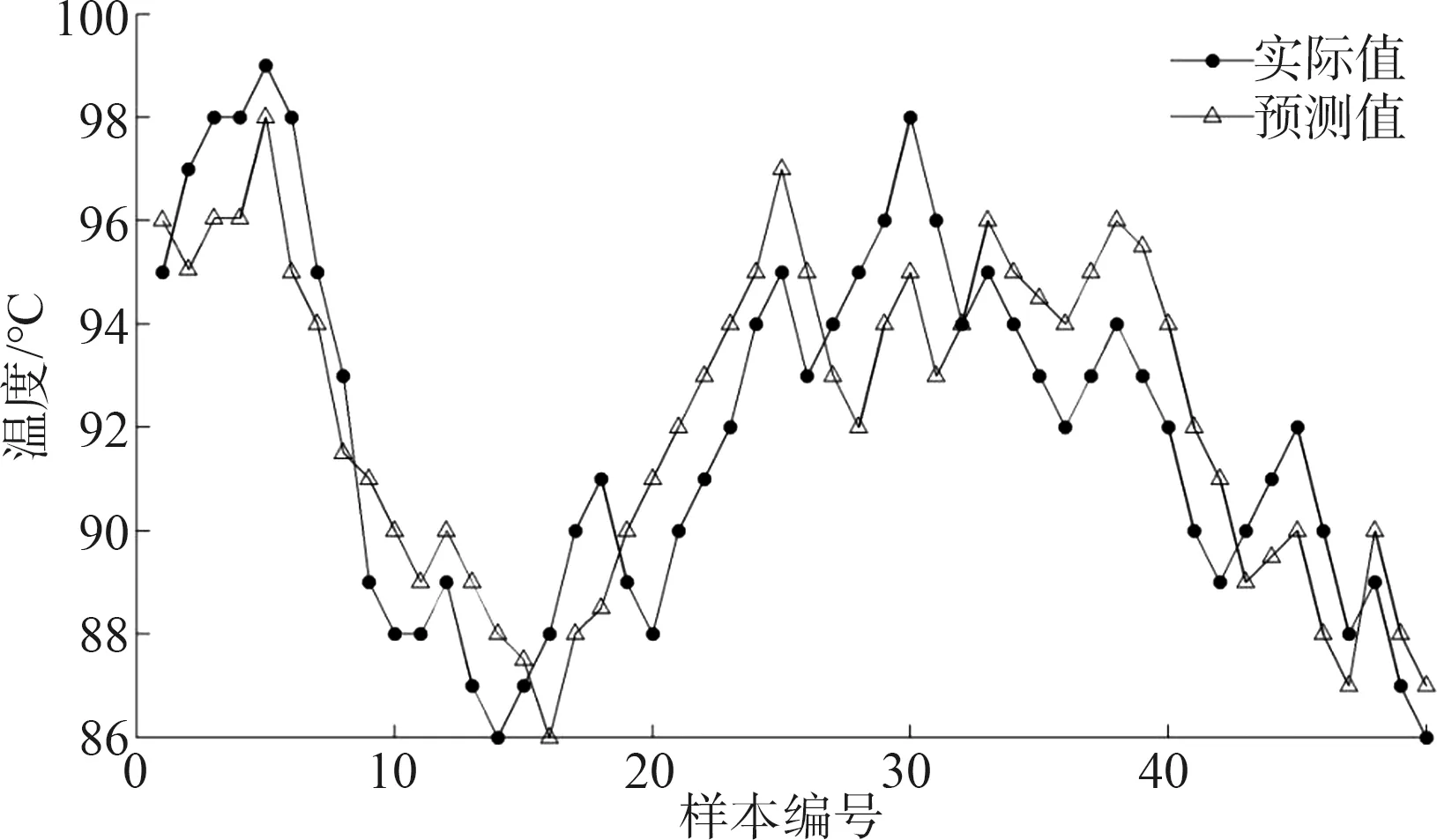
图3 测试集数据预测结果

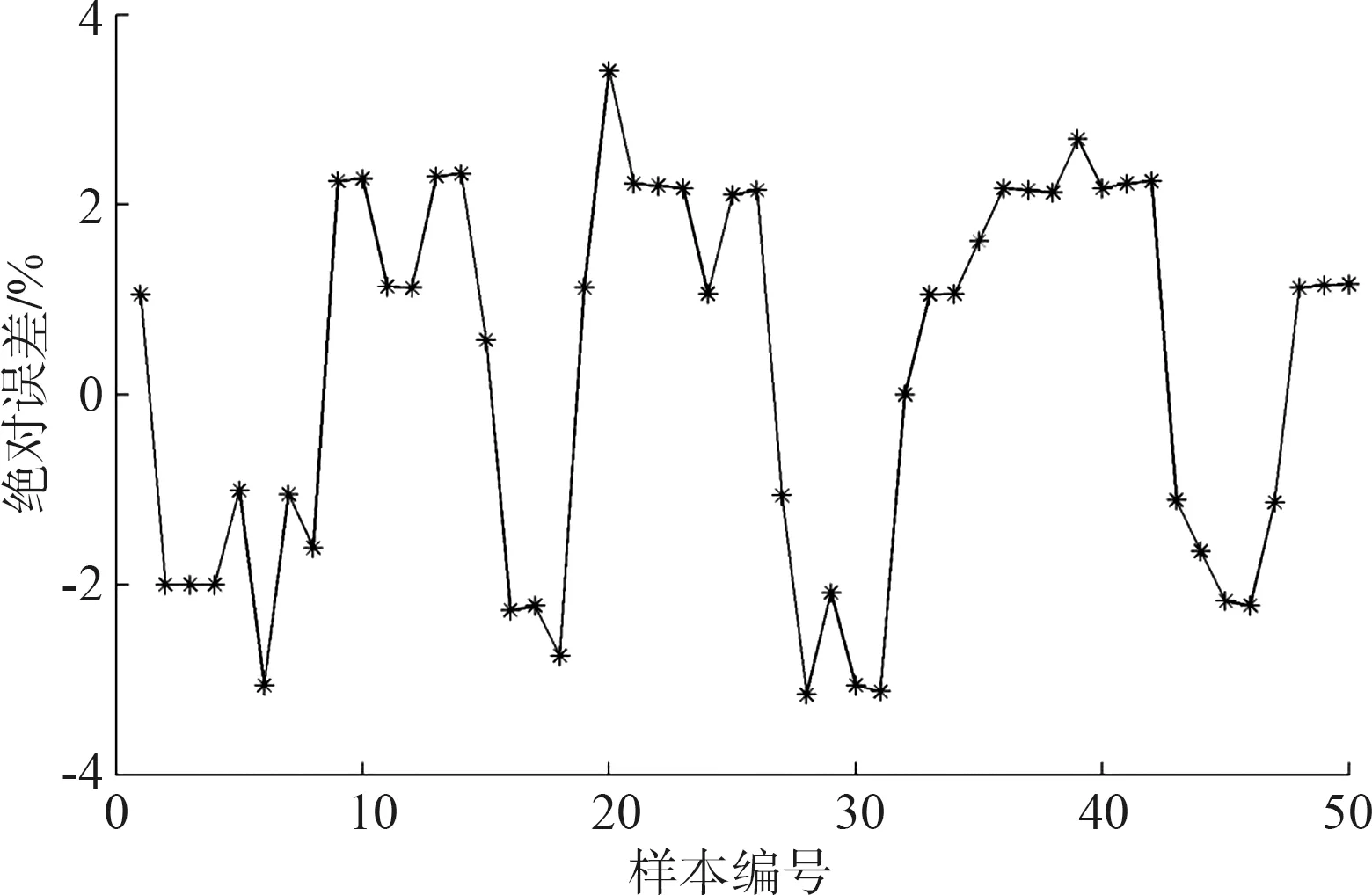
图4 测试集数据绝对误差

由图3可知，基于GA-BP神经网络的变压器绕组热点温度预测值与实际值的变化趋势基本一致，由图4可知，测试集数据预测的绝对误差都在±4%内，且大部分误差集中在±2%左右，可见GA-BP神经网络应用于变压器绕组热点温度预测的效果较好。

为了检验模型的预测精度，本文采用平均相对误差和均方根误差对基于GA-BP神经网络的变压器绕组热点温度预测效果进行评价，计算公式如下：

(17)

(18)

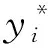
采用同样的样本数据建立BP、SVM以及ELM预测模型，利用测试集数据进行检验，4种预测模型的平均相对误差和均方根误差如表2所示，由表2可知，基于GA-BP神经网络的变压器绕组热点温度预测的平均相对误差和均方根误差分别为2.05%和0.21，在4种预测模型中均为最小，进一步验证了本文提出方法的正确性。

表2 4种模型预测误差

4 结论

a.采用遗传算法对BP神经网络的权值和阈值进行修正，解决了BP神经网络容易陷入局部最小值的缺陷，加快了算法的收敛速度，并将其应用到变压器绕组温度预测领域，建立了基于GA-BP神经网络的变压器绕组热点温度预测模型。

b.利用500组变压器试验数据进行仿真，结果表明，基于GA-BP神经网络的变压器绕组热点温度预测值与实际值的变化趋势基本一致，平均相对误差和均方根误差分别为2.05%和0.21，相比于其他几种预测方法，预测效果最好，验证了该方法的正确性。