基于动态模糊神经网络的超临界机组协调控制
2021-04-08马良玉郑佳奕
马良玉, 郑佳奕
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
0 引 言
超临界机组采用直流锅炉,具有大时滞、多变量、非线性和强耦合等特点,且考虑到锅炉和汽轮机各自的动态特性,传统的机组协调控制方法往往难以适应电网自动发电控制(AGC)快速变负荷及深度调峰的运行要求。因此研究调节品质高的新型优化控制策略,成为火电厂研究的热点课题。
许多学者基于线性理论与非线性系统理论对火电机组协调控制进行了深入研究。文献[1]借助H∞控制理论对不同工况点下的线性模型设计了多变量鲁棒PID控制器;文献[2,3]在某1 000 MW的超超临界机组非线性模型的基础上,分别进行非线性内模控制和基于稳定逆的前馈-反馈控制策略研究;文献[4]针对超超临界机组协调控制,利用Gap metric理论分析机组非线性特征,进而研究协调系统多模型预测控制策略。文献[5]提出一种基于自适应反演算法的火电单元机组协调控制策略。然而,对于大时延、多变量的协调控制系统来说,由于各种干扰的存在,及系统结构、参数运行中可能发生变化,其精确的数学模型难以获得,即使能够建立数学模型,控制器的参数整定往往过于复杂,使理论方法应用于工程实践受到影响。
近年来,在火电厂过程控制领域出现了各种各样的新型智能控制策略[6-9],为解决上述问题带来了新的思路。文献[6]将模糊推理与自适应控制相结合,提出了在工程上可实现的智能解耦方法;文献[7,8]针对超临界机组控制特点,建立了锅炉汽压和负荷特性的神经网络逆模型,进而设计了协调系统逆控制方案并进行了仿真研究;文献[9]提出了一种基于神经网络和粒子群(PSO)算法的协调预测优化控制方法,仿真试验表明该方法可有效提高机组的协调控制效果。然而,由于神经网络模型结构优选缺乏固定的规律性,建模时只能通过反复试验来确定其结构及权值、阈值等参数[10]。这不仅增加了建模耗时,也不利于模型进行在线自学习,如何进一步提高模型的精度和泛化能力、实现机组特性变化时模型的在线自校正是亟待突破的研究方向。
为此,本文基于动态模糊神经网络(Dynamic Fuzzy Neural Network,DFNN),以某600 MW超临界机组为对象,利用历史样本数据离线建立了机组负荷、汽压特性的逆模型,并确定了离线训练与在线校正相结合的DFNN逆控制方案。通过与600 MW机组的全范围仿真机进行实时双向数据交换,开展详细的控制仿真试验。结果表明:采用所设计的DFNN逆控制方案,大幅变工况下机组负荷和主汽压响应的快速性与机组原控制相比有很大提高,有效改善了机组协调控制对AGC快速变负荷的适应能力。
1 动态模糊神经网络
1.1 动态模糊神经网络的结构
动态神经网络(DFNN)的结构如图1所示。
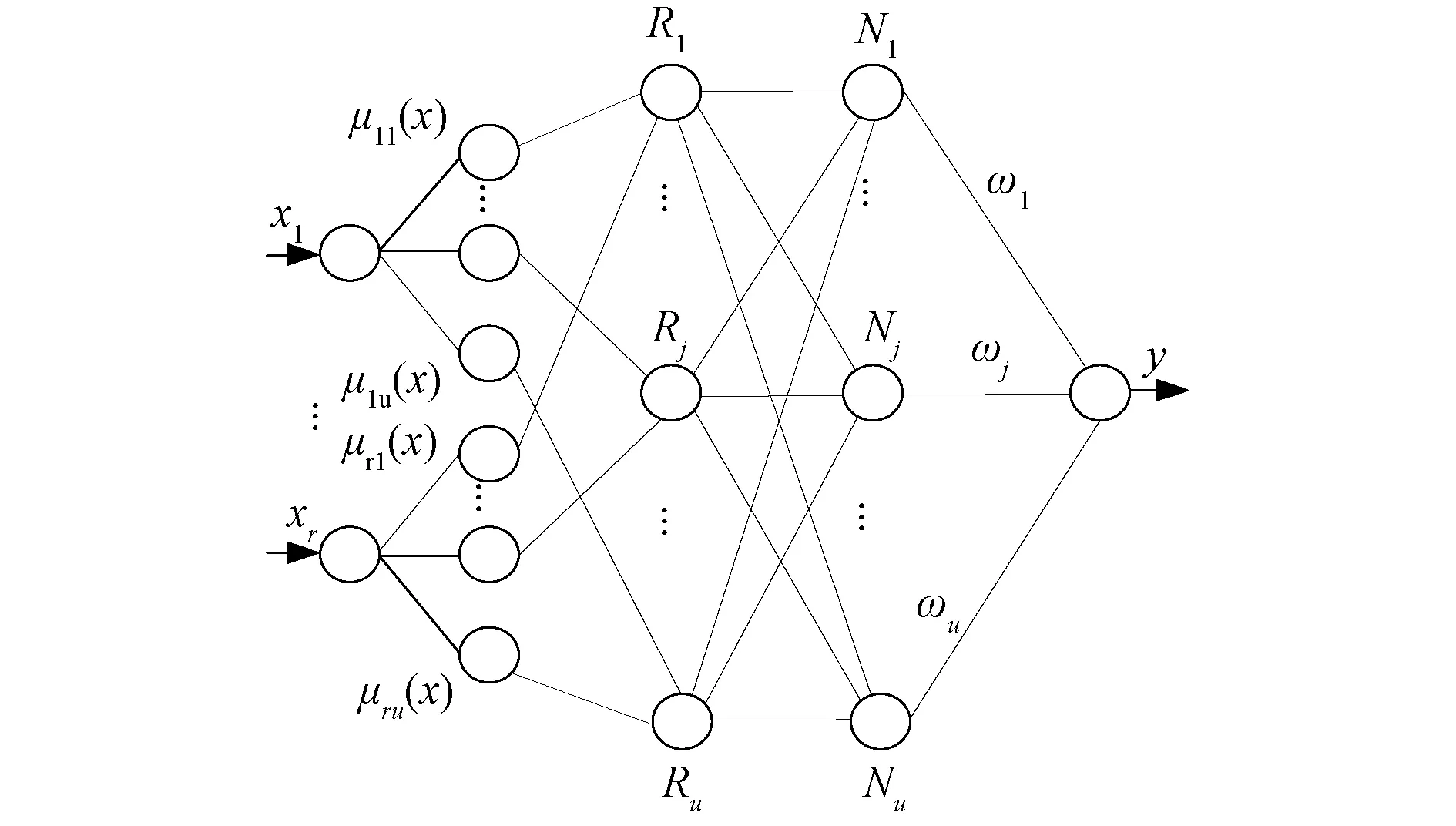
图1 DFNN算法Fig.1 Algorithm of DFNN
DFNN的第一层为输入层;第二层是隶属函数层,其每个节点都代表一个隶属函数(高斯函数)。第三层是模糊规则层,其每一个节点都代表一条模糊规则;第四层是对第三层的输出进行归一化;第五层是输出层。DFNN中输出y关于输入X=(x1,…,xr)T的表达式为
(1)
式中:Rj为DFNN第三层的输出;Nj为第四层的输出;ωj为第四层到输出层的连接权值,是关于输入xi的线性函数,aij为线性系数。Cj=(cij,c2j,…,crj)T为第j个模糊规则下的高斯函数中心向量;σj是第j个模糊规则下高斯函数的宽度。其中,i=1…r;j=1…u,r为输入样本的维度;u为总的模糊规则数。
1.2 动态模糊神经网络的学习算法
1.2.1 模糊规则的确定
在图1所示模糊神经网络中,如果模糊规则数过少,系统将不能涵盖所有的输入输出状态。但如果模糊规则数过多,又会导致DFNN的过度拟合。对于模糊规则数的确定,可引入下述两个判据[11,12]:
(1) 系统误差判据
对于第k个观测数据(Xk,tk),其中,tk是期望的输出,定义系统误差:
‖ek‖=‖tk-yk‖
(2)
如果‖ek‖>ke,则需要增加一条新的模糊规则。这里的ke根据DFNN期望的精度预先选定。
(2) 可容纳边界
如果一个新样本位于某个存在的高斯函数的覆盖范围(即可容纳边界)内,该样本就可以用已经存在的高斯函数代表,而无须产生新的高斯函数。
对第k个观测数据(Xk,tk)计算输入值Xk和现有的高斯函数单元的中心Cj之间的距离dk(j),即
dk(j)=‖Xi-Cj‖j=1,2,…,u
(3)
令dmin=min(dk(j)),如果dmin>kd,则要考虑增加一条模糊规则。否则该输入数据可以由现有的最近的高斯函数表示。这里kd是可容纳边界的有效变量。
当进行模型的离线训练时,可对ke和kd进行动态调节:首先设置比较大的ke和kd,确定产生输出误差大而没有被现有模糊规则覆盖的位置。进一步,通过网络的训练,按照式(4)、(5)不断缩小ke和kd:
ke=max[emax×βi,emin]
(4)
kd=max[dmax×γi,dmin]
(5)
式中:emax为预先定义好的最大误差;emin为期望的DFNN精度;β(0<β<1)为收敛常数;dmax为输入空间的最大长度;dmin为最小长度;γ(0<γ<1)为衰减常数。
基于上述两个指标,考虑以下4种情况:
(1) 当‖ek‖≤ke,dmin≤kd时,说明DFNN可以完全描述所有样本点,不需要增加模糊规则。
(2) 当‖ek‖≤ke,dmin>kd时,说明DFNN具有较好的泛化能力,不需要增加模糊规则。
(3) 当‖ek‖>ke,dmin>kd时,需要增加一条模糊规则。
(4) 当‖ek‖>ke,dmin≤kd时,表明尽管Xk可以聚集在已有的高斯函数附近,但覆盖Xk的高斯函数泛化能力并不是很好。因此,不需要增加模糊规则,但高斯函数的σ和结果参数ω需要被更新。
1.2.2 前提参数的初始化与动态调节
对第k个观测数据Xk,当需要增加第j条模糊规则时,对其Cj和σj进行初始化:
Cj=Xk
(6)
(7)
其中,kl(kl>1)为重叠因子。kl越大,说明每个隶属函数之间的重叠度越大。
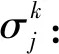
(8)
其中,kω(kω>1)是预设常数。
1.2.3 结果参数的确定
假设n个样本点产生了u个模糊规则,对于第k个观测数据Xk,系统的输出yk由式(1)计算,也可将式(1)写为如下形式:
WΨ=Y
(9)
假定理想的输出为T=(t1,t2,…,tn)∈Ξn,规定性能指标函数为
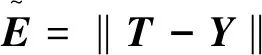
(10)
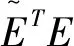
W*×Ψ=T
(11)
最优的W*具有如下形式:
W*=T(ΨTΨ)-1ΨT
(12)
1.3 模糊规则的实时剔除
在DFNN的学习过程中,如果检测到某一个模糊规则逐渐对系统失去了贡献作用,加以剔除便会获得更紧凑的DFNN结构。采用误差下降法作为剔除模糊规则的策略[12]。首先将式(9)和式(10)写成线性回归模型的形式:
TT=ΨTWT+E
(13)
令D=TT∈Ξn,H=ΨT=(h1,h2,…,hv)∈Ξn×ν,v=u×(r+1),θ=WT有
D=Hθ+E
(14)
其中,E∈Ξn是与hi不相关的误差向量。
对于任意矩阵H,如果它的行数大于列数,通过QR分解:
H=QA
(15)
其中,Q的各列向量qi构成正交基,并且A∈Ξν×ν为一个上三角矩阵。通过这一变换,就可以计算每一个个体对输出性能指标的贡献。
联立式(14)和式(15)可得
D=QAθ+E=QG+E
(16)
G的线性最小二乘解为
G=(QTQ)-1QTD
(17)
设gi为G的列向量,可将上式改写为
(18)
当i≠j时,因为qi与qj正交,D的平方和由下式给出:
(19)
(20)
将式(18)带入式(20)中得
(21)
上述方程中,如果erri值很大,表明qi和D的相似程度大,即qi对于输出影响显著。把erri(i=1,…,(r+1)u)重新排列为矩阵Δ=(δ1,δ2,…,δu)∈Ξ(r+1)×u,Δ的第i列δi就是与第i个规则相关的(r+1)个误差下降率。定义ηi为第i个规则的重要程度:
(22)
ηi越大表明第i个规则越重要。若满足:
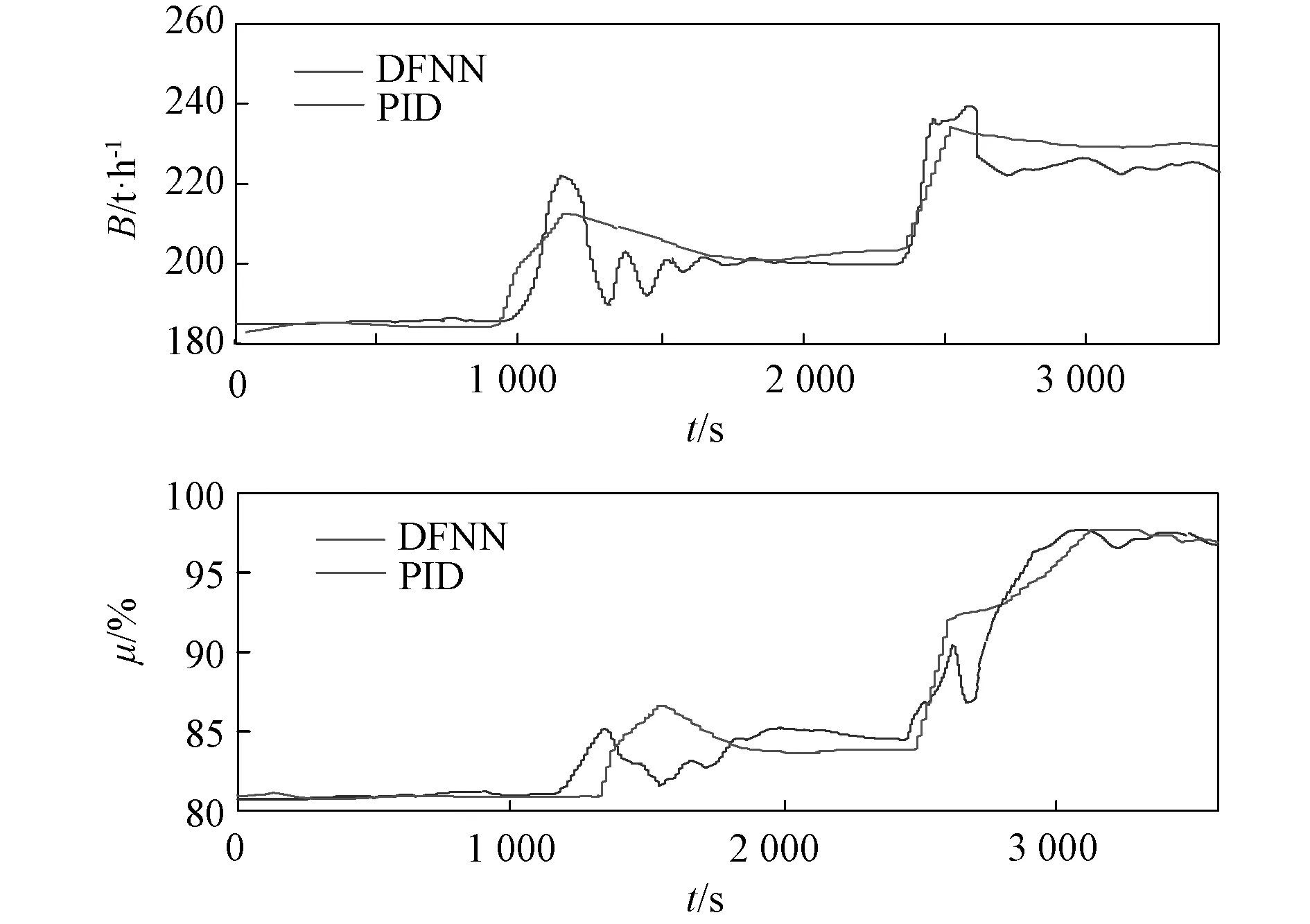
ηi (23) 则第i个规则可剔除。其中,kerr表示规则重要性的阈值。 超临界机组参与AGC的变负荷过程中,应优先满足电网负荷需求。以锅炉跟随为基础的协调控制(BFCC)模式,依靠汽机调门迅速改变机组负荷,并由锅炉侧燃料、给水等子系统的调节维持汽压、汽温等参数稳定,这种模式最适应AGC负荷快速响应的要求。将超临界机组划分为锅炉和汽轮发电机组两部分,由机理分析可知,与机组负荷直接相关的参数包括主汽压力、主汽温度及汽轮机调门开度等;主汽压力则受给水量、锅炉侧燃料量和汽机侧调门开度的共同影响[7,8]。据此本文采用如下建模思路: (1) 协调控制对象逆模型的建立基于BFCC运行模式; (2) 以汽轮机调门为界,分别针对锅炉和汽轮机建立主汽压力和机组负荷的逆模型:汽机侧调门开度调节负荷,燃料量维持主汽压力。逆模型结构如图2所示。 图2 超临界机组负荷、主汽压特性逆模型Fig.2 Inverse models for load and main steam pressure of supercritical unit 2.2.1 仿真试验平台简介 STAR-90系统是华北电力大学开发的电站仿真平台。它具有图形化的仿真建模系统和高精度的电站算法库,便于模型的调试、修改和扩展。高精度和良好动态特性的电站全工况仿真模型可为控制理论的研究提供可靠的准工业试验环境。本文训练数据的获取、仿真试验的开展都是在由STAR-90系统开发的600 MW超临界机组全范围仿真机上进行的。 2.2.2 DFNN逆模型的离线训练 以DFNN为基础,采用具有输入时延和输出反馈时延的网络结构建立负荷、汽压特性的逆模型。具体如下: 将图2 (a) 中P(k)、T(k)、Ne(k)、P(k-1)、T(k-1)、Ne(k-1)、μ(k-1)作为DFNN的输入,μ(k)作为输出,构建负荷特性逆模型;将图2 (b) 中μ(k)、W(k)、P(k)、μ(k-1)、W(k-1)、P(k-1)、B(k-1)作为DFNN的输入,B(k)作为输出,构建主汽压特性逆模型。 为提高DFNN逆模型的泛化能力,网络训练样本所涉及的工况应包括不同负荷下的稳态工况数据和变负荷动态过程中的运行数据。数据收集过程中,机组在BFCC模式下运行,燃料、给水、汽机调门、风量、各级过热汽温等控制均在自动模式。变负荷率为12 MW/min,变压速率为1 MPa/min。提取的训练数据包含600 MW到360 MW之间不同负荷点的稳态数据,以及在各工况间连续降、升负荷的动态数据,共12 000组(采样时间为1 s)。上述数据经归一化处理后用于DFNN逆模型的训练,DFNN网络训练参数选取选择见表1,训练过程中模糊规则与均方根误差(RMSE)随输入样本x增多而产生的变化如图3和图4。训练后模型的拟合效果如图5所示。 表1 DFNN网络训练参数选取 图3 训练时的模糊规则数变化 Fig.3 Numerical change of fuzzy rules during training 图4 训练时的拟合误差(RMSE)的变化 Fig.4 Change of fitting error (RMSE) during training 图5 训练集的拟合效果Fig.5 Fitting effect on training set 为检验该DFNN逆模型在不同于训练工况下的预测精度和泛化能力,将变负荷率设为18 MW/min,同样在600 MW至420 MW之间连续分段升降负荷,共获得12 000组数据进行校验。拟合效果如图6所示。 图6 测试集的拟合效果Fig.6 Fitting effect on test set 可见,上述负荷、主汽压特性DFNN逆模型可以快速地完成训练,并具有较好地拟合精度。对于不同于训练样本的验证工况,训练好的DFNN逆模型仍然具有较好的拟合效果。 基于训练好的负荷、主汽压特性逆模型,分别构建基于负荷和主汽压特性的DFNN逆控制器,对机组的负荷、主汽压进行控制。在实施控制时,逆模型B通过每个控制周期中采集的实时数据进行自校正,30 min替换用于控制的逆模型A。负荷、主汽压的DFNN逆控制原理图如图7所示。 图7 DFNN控制原理图Fig.7 Schematic diagram of DFNN control 对于逆模型B,采用梯度下降法调整DFNN的前提参数和结果参数,文献[12]表明高斯中心对系统性能影响不大,因此前提参数中只对高斯宽度进行更新。 这里取误差的负梯度作为性能指标: (24) 结合式(9),由链式规则可得 (25) 2ξ(t-y)·ω(k,j)·Rj·‖P-Cj‖2/σj3 (26) 式中:η和ξ分别为结果参数和高斯宽度训练的学习率。 考虑到随着输入数据量的增加,DFNN的训练时间会长于控制器的样时间。因此,应该设置固定的数据长度L,当采集的数据量大于L时,将添加新数据并删除旧数据。 同时为了提高控制效果,需要结合神经网络逆控制和闭环反馈控制的优点[13]。以机组负荷和主汽压力的原始设定值为参考,根据当前k时刻负荷和主蒸汽压力的反馈值实时调整逆控制器的输入Nref和Pref: Nref(k+1)=Nref(k)-k1(Ne(k)-NSP(k)) (27) Pref(k+1)=Pref(k)-k2(Pt(k)-PSP(k)) (28) 式中:Nsp(k)及Psp(k)分别为负荷及主汽压在k时刻的设定值;k1和k2分别为负荷和主汽压参考值的调节系数。 在BFCC模式下,需要通过快速调节汽轮机阀门以更好地满足负荷需求,使机组负荷优先变化。因此,主蒸汽压力有可能产生较大偏差。为了减小初始动态阶段的主蒸汽压力偏差,在k2中引入负荷目标值和负荷变化率,如式(29)和式(30)所示: k2=max(k3,k3×kzoom×Tardif(k)×Nerate/12) (29) Tardif(k)=|(Ne(k)-Netar_new)/(Netar_old-Netar_new)| (30) 式中:Netar_old为变负荷前的稳态值;Netar_new为新的目标值;Nerate为变负荷速率;kzoom为负荷开始变化时用于加速燃料侧变化的扩张系数,当Ne接近Netar_new时,燃料侧变化速度会逐渐变慢。 基于上述DFNN逆控制方案,在MATLAB平台上开发了实时控制算法和通信程序,并通过与600 MW超临界机组仿真机进行双向数据交换开展仿真试验。在试验过程中,给水、过热、再热等子系统均设置为自动控制模式。负荷变化率设定为12 MW/min,主汽压变化率设定为1 MPa/min。DFNN控制器的相关参数如表2所示。 表2 DFNN控制器相关参数 在试验过程中,设置煤质(发热量)发生2%到5%的扰动。将变负荷率设为12 MW/min,变压速率设为1 MPa/min,分别采用DFNN逆控制和机组原PID进行试验:先降负荷,从600 MW定压降负荷至540 MW稳定后滑压降至480 MW。负荷和汽压控制效果对比如图8,汽轮机的调门开度和燃料量的变化如图9所示。 再升负荷:从480 MW滑压升负荷至540 MW稳定后定压升负荷至600 MW。负荷和汽压控制效果对比如图10,汽轮机的调门开度和燃料量的变化如图11所示。 图8 降负荷试验中负荷和主汽压的控制效果Fig.8 Control effect of load and main steam pressure in load drop test 图9 降负荷试验中汽轮机调门开度与燃料量的变化Fig.9 Change of turbine regulating valve opening and fuel flow rate in load drop test 图10 升负荷试验中负荷和主汽压的控制效果Fig.10 Control effect on load and main steam pressure in load rise test 图11 升负荷试验中汽轮机调门开度与燃料量的变化Fig.11 Change of turbine regulating valve opening and fuel flow rate in load rise test 综合对比上述升、降负荷试验结果可看出:机组原协调控制,PID控制器参数设置过于求稳,导致负荷和主汽压力变化较慢,滞后大,稳定时间长,不能适应AGC快速变负荷的要求,有必要针对不同工况对各PID控制器参数进行寻优。而采用本文DFNN逆控制器后,机组在负荷调节的快速性、动态偏差、稳定时间等指标方面明显优于原PID控制,能较好地适应AGC快速变负荷要求。同时,由于DFNN逆控制在变负荷过程引入燃料量前馈,主汽压滞后较小,变负荷过程能较好地跟踪汽压设定值曲线,动态偏差较小。尽管负荷刚开始变化及刚趋稳时主汽压有超调,但最大偏差小于0.8 MPa,不影响机组运行安全性。 本文针对超临界机组大时滞、多变量、非线性和强耦合等特点,基于以锅炉跟随为基础的协调控制方式,建立了超临界机组负荷、主汽压特性的动态模糊神经网络逆模型。在此基础上,设计了一种协调系统DFNN逆控制方案;在MATLAB平台上编制了DFNN逆控制算法;借助火电机组全范围仿真系统开展了仿真试验研究,结果表明: (1)与原机组协调控制相比,协调系统采用DFNN逆控制方法,机组负荷、主汽压调节的快速性方面有很大的提高,验证了基于DFNN逆控制的良好效果。 (2)不同于以往的神经网络逆控制,本文通过引入DFNN算法,使得控制器能够在满足实时控制的前提下完成自校正,这有利于提升机组在煤质改变、锅炉特性改变或大范围变工况时的负荷跟踪能力、抗干扰性能。 总的来说,模糊神经网络作为一个强有力的建模工具,已广泛地应用到各个领域。尤其是离线训练和在线校正相结合的动态模糊神经网络,学习速度快,更适合于实时控制应用。希望通过进一步的研究和试验,最终应用于实际电站优化控制,发挥更大作用。2 超临界机组负荷汽压特性建模
2.1 超临界机组负荷汽压特性建模方案确立

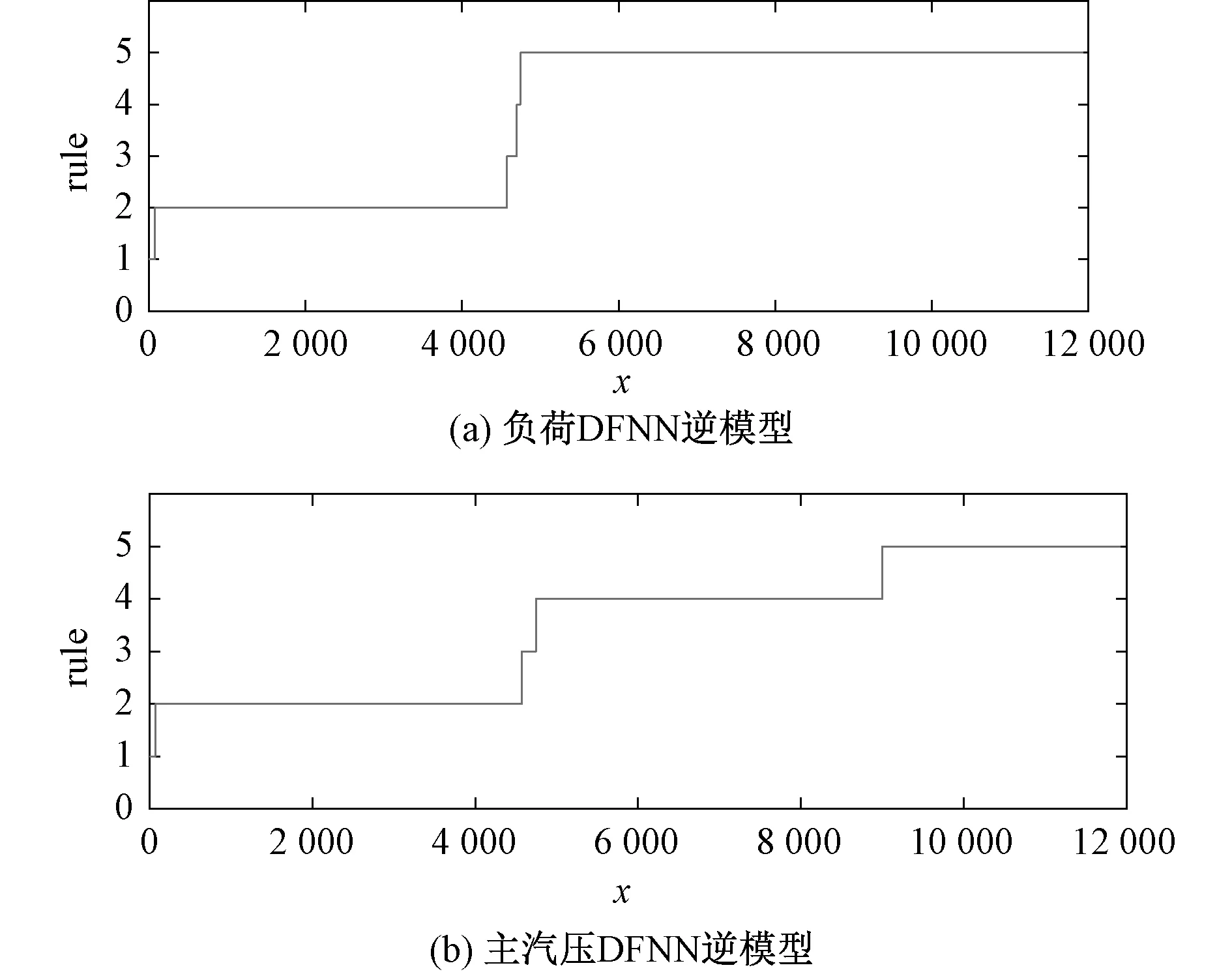
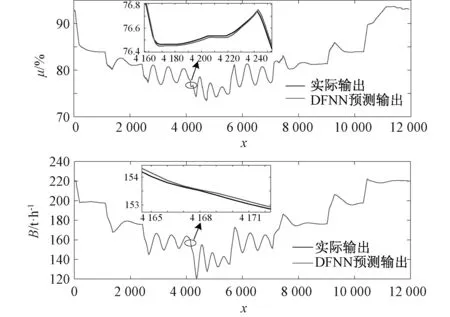
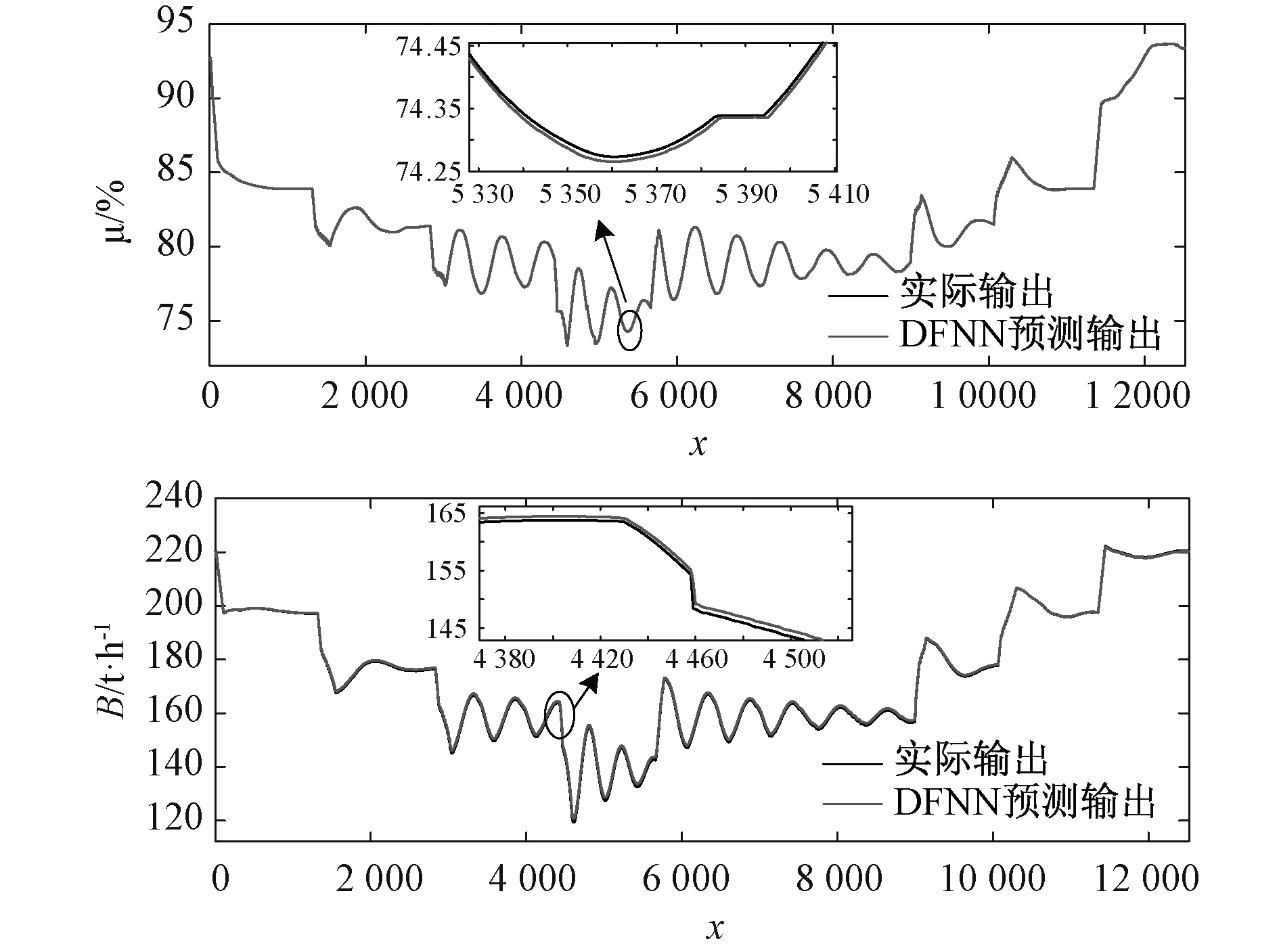
2.2 负荷-主汽压DFNN逆模型的训练


3 协调系统控制方案设计与仿真
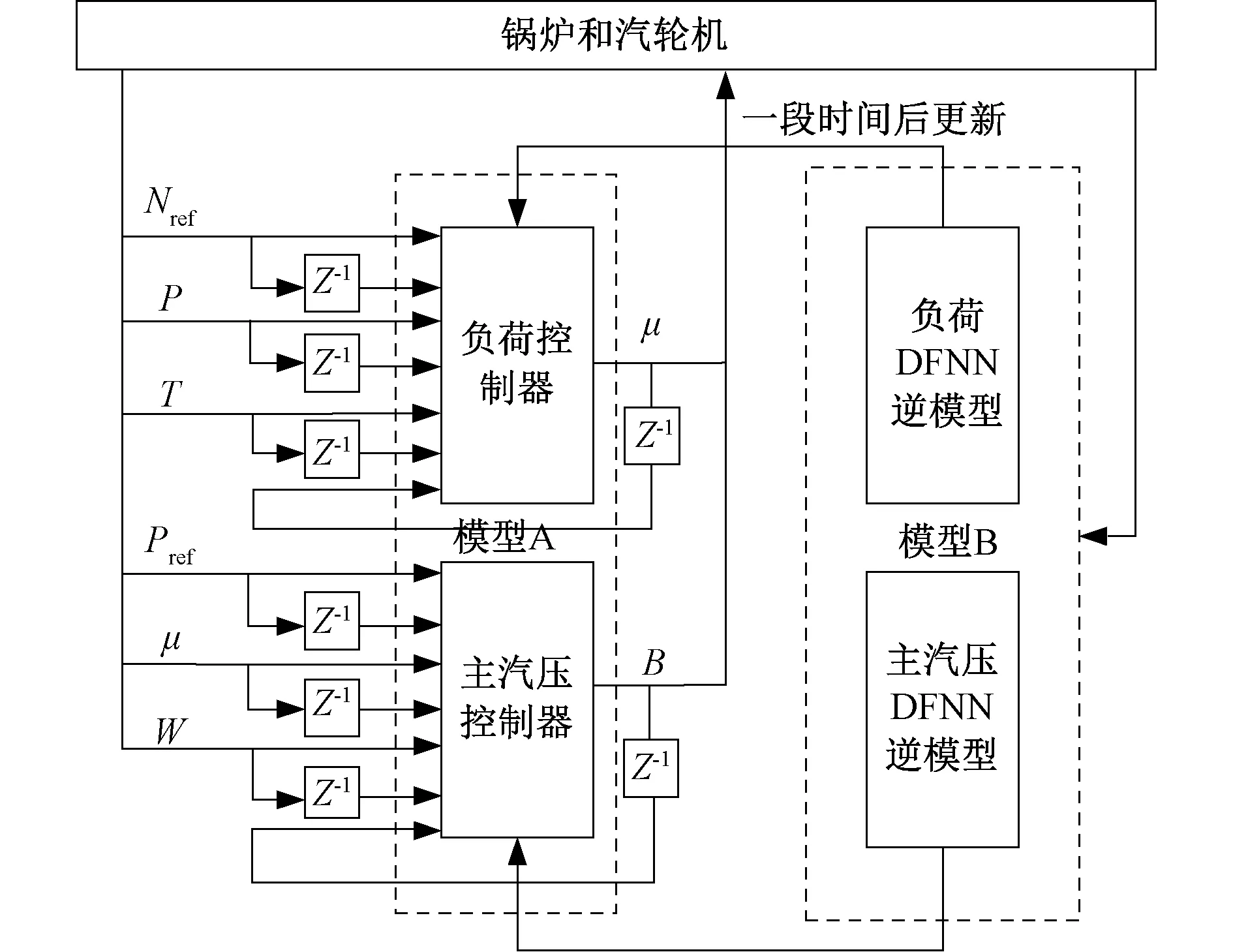
3.1 协调系统神经网络逆控制方案
3.2 仿真试验
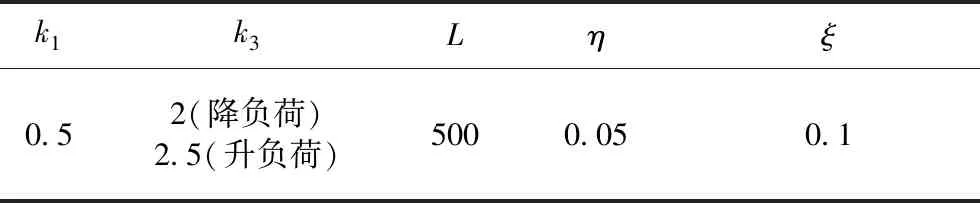
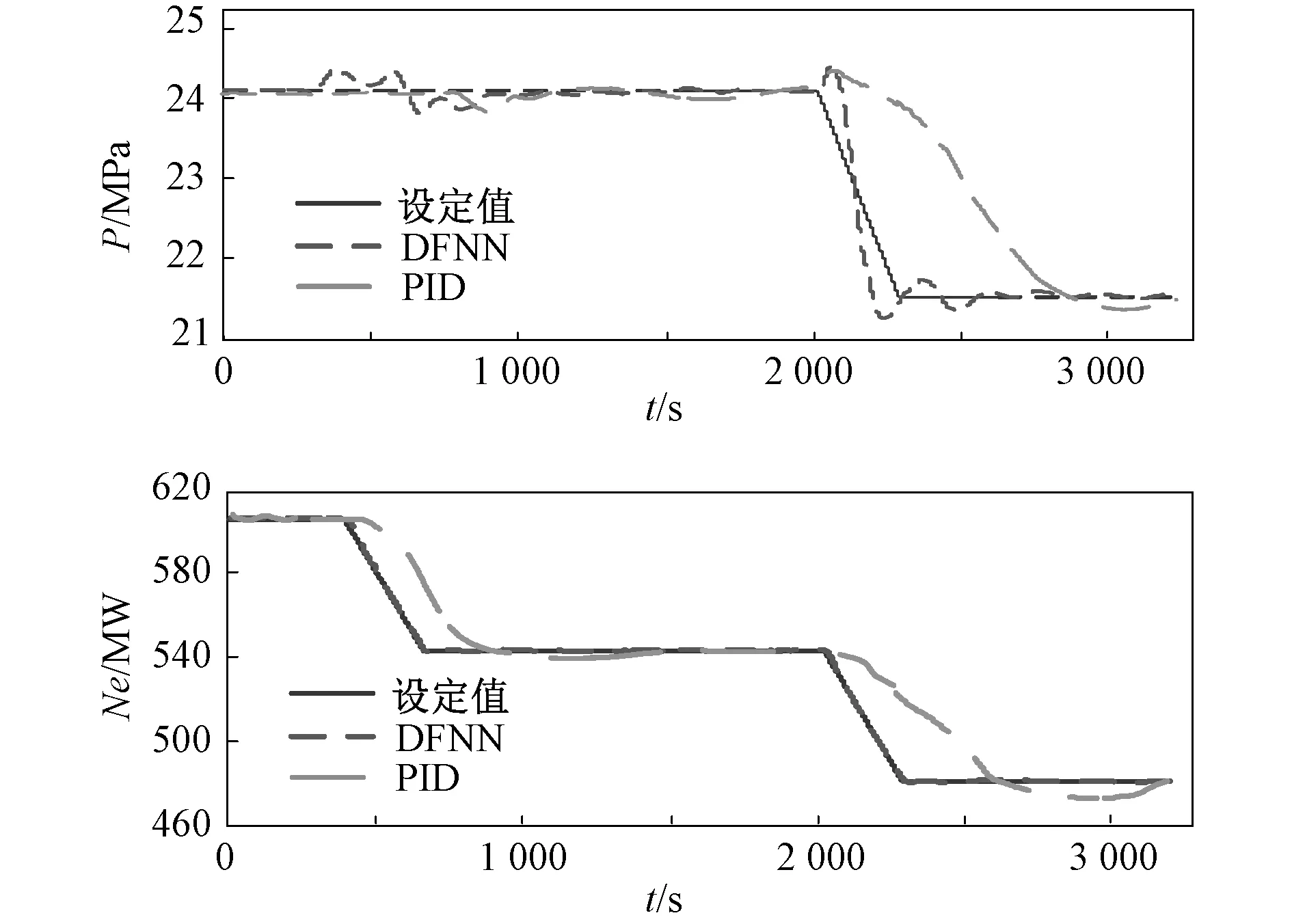
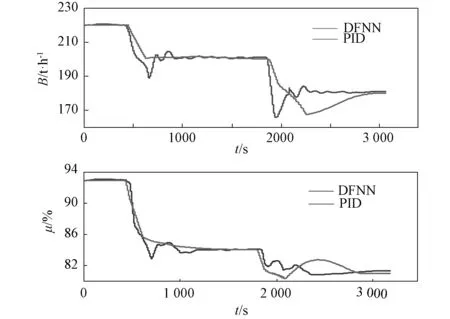
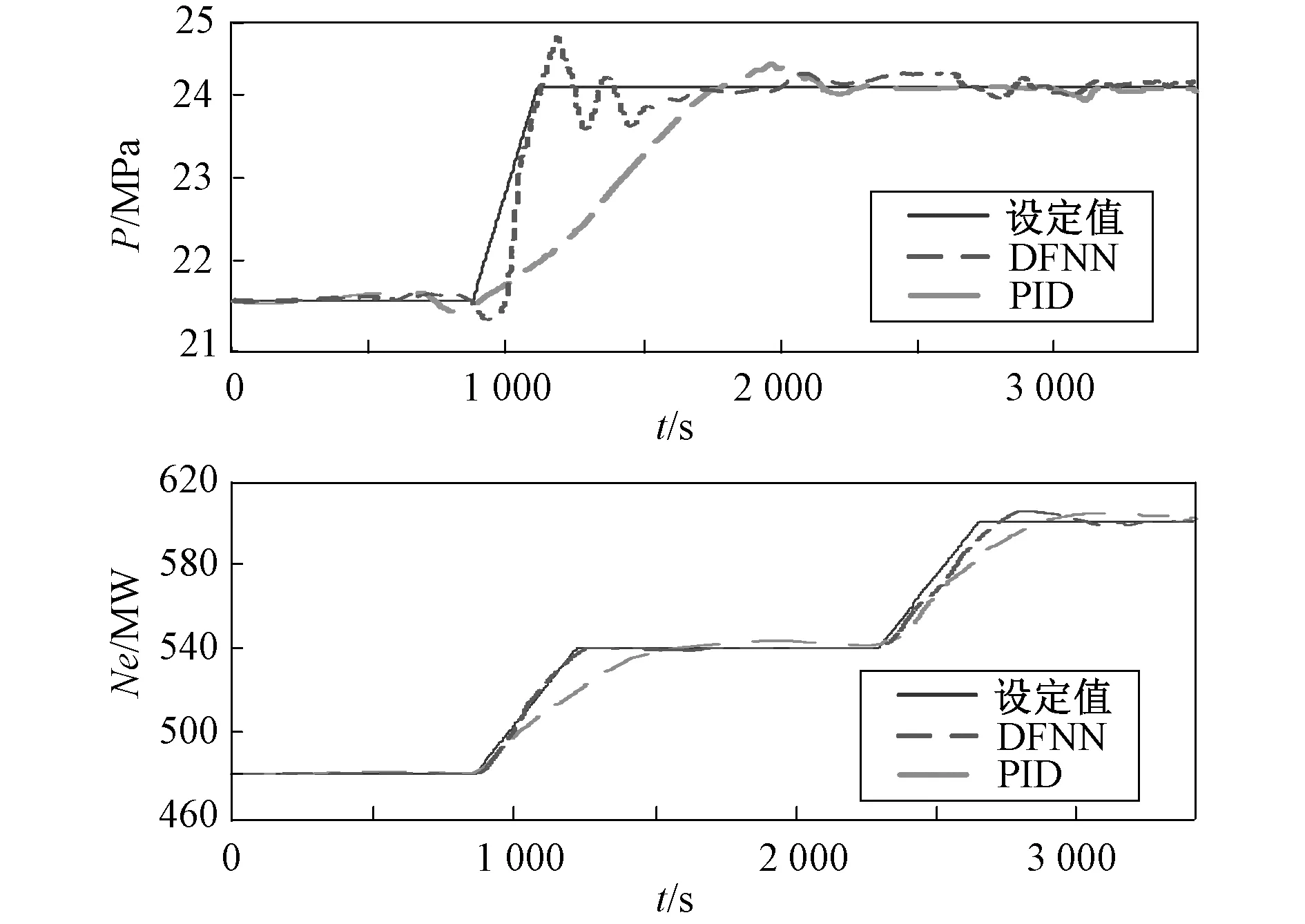
4 结 论
