基于卡尔曼滤波器的循环流化床机组燃料发热量软测量
2021-04-08李泽铭
李泽铭, 田 亮
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
0 引 言
当前电厂发电燃煤来源日趋复杂,煤质难以保证,煤发热量变化频繁且剧烈[1]。循环流化床锅炉(CFB)具有燃料适应性广,燃烧效率高等优点。 但煤发热量剧烈变化依然是其运行状态检测和控制面临的主要问题之一。原因如下:首先是CFB本身设计可燃烧劣质煤种,且许多CFB位于城市周边,在运行过程中会掺烧秸秆、垃圾、淤泥等低热值物质,人为造成入炉燃料发热量变化。其次是电网发电指令负荷波动剧烈,为跟随负荷指令,燃烧总热能也要相应变化。由于燃料发热量变化频繁,为保持机组运行状态稳定要求控制燃料量做出快速改变。基于以上原因CFB燃料发热量实时准确测量是非常有必要的。受限于技术、成本等方面原因,煤发热量难以直接测量,软测量是工程中应用较多的方法之一。
目前已有多种燃料发热量软测量方法。美国Leeds & Northrup公司在DEB(Direct Energy & Balance)协调控制系统中构造了一种用作反馈控制量的热量信号。该信号用汽轮机一级压力和锅炉汽包压力微分计算出,可以反映燃料量和发热量变化但存在较大延迟[2,3]。文献[4]研究通过燃料热值(BUT)校正消除燃料发热量变化对协调控制系统影响到方法,BTU校正的核心逻辑是计算燃料发热量。但通过该方法得到的燃料发热量只在稳态工况下准确,当燃料热值波动时,反应不出其变化情况,具有较大动态误差;文献[5]针对BTU校正法测量燃料发热量动态特性差难以快速反应实际燃料发热量变化的缺点。提出利用机组负荷-压力模型来计算燃料发热量的方法。文献[6]提出了一种利用锅炉风量和排烟氧量计算热量的方法。以上两种方法能快速反应燃料发热量变化大小但其测量值不准确。为既快又准的测量燃料发热量,文献[7]针对600 MW机组,根据化学分析得到的具有较高静态精度燃料发热量信号和机组负荷-压力模型计算的具有良好动态特性的燃料发热量信号互补的特点,采用卡尔曼滤波器进行融合。
但由于CFB实际运行时具有燃料发热量信号延迟更大(通常燃料完全燃烧转化为电能这一过程需要至少30 min)、燃料种类更多、煤质变化更大等特点,所以控制机组跟上快速波动的负荷指令愈加困难。这使得快速准确测量CFB燃料发热量具有更加重要的意义。
1 卡尔曼滤波基本原理
考虑用如下状态状态方程和测量方程描述控制系统:
x(k)=Ax(k-1)+Bu(k)+w(k)
(1)
z(k)=Hx(k)+v(k)
(2)
式中:k为离散时间,系统在时刻k的状态为x(k)∈Rn;对应状态的观测信号为z(k)∈Rm;w(k)∈Rr为输入的白噪声,v(k)∈Rm为观测噪声。两者是均值为零,方差矩阵各为R1和R2的不相关白噪声且初始状态x(0)不相关于w(k)和v(k)。式(1)为状态方程,式(2)为观测方程。其中A为状态转移矩阵,B为输入矩阵,H为观测矩阵。
利用如上的控制系统模型,进行卡尔曼滤波,具体步骤如下:
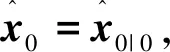
(2)用k-1时刻的最优估计值来预测k时刻的先验估计值。
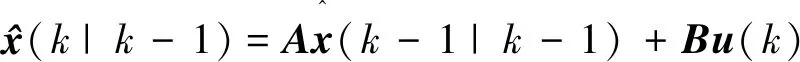
(3)

(3)根据k-1时刻最优估计协方差阵P(k-1 |k-1)进一步预测k时刻先验估计协方差阵P(k|k-1)。
P(k|k-1)=AP(k-1|k-1)AT+R1
(4)
式中:R1为过程噪声w(k)的协方差阵。
(4)进一步推导k时刻滤波增益矩阵g(k)。
g(k)=P(k|k-1)HT[HP(k|k-1)HT+R2]-1
(5)

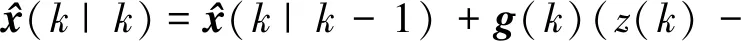
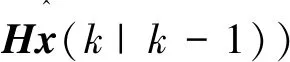
(6)
式中:z(k)为系统测量值;g(k)为k时刻滤波增益矩阵;H为观测矩阵。
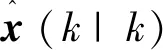
(7)
式中:P(k|k)为k时刻最优估计协方差阵。
(7)将公式(5)代入公式(7)得化简后的k时刻最优估计协方差阵P(k|k)。
P(k|k)=(I-g(k)H)P(k|k-1)
(8)
当系统进入k时刻的状态时,P(k|k)变为下一时刻中的P(k-1|k-1)。x(k|k)变为下一时刻中的x(k-1|k-1)。按照以上公式循环下去即可得到每一时刻的卡尔曼最优估计x(k|k)。
2 燃料发热量软测量法
2.1 通过发热量BTU校正系数得到燃料发热量
在锅炉燃烧过程中常利用直接能量平衡(DEB)中的热量信号来反应燃料量变化情况。同时,在控制系统中还利用设计煤种热值与理论煤种的热值之比校正燃料量,即实际燃料量可由理论燃料量和煤种热值校正系数(BTU)计算得出[8,9]。
传统BTU校正系数计算原理如图1:将给水流量带入“给水流量-燃料量函数f1(x)”计算出理论燃料量。令BTU校正后的实际燃料量减去理论燃料量经由一个积分环节后将结果折算为0.8~1.2之间的数值,即BTU校正系数。
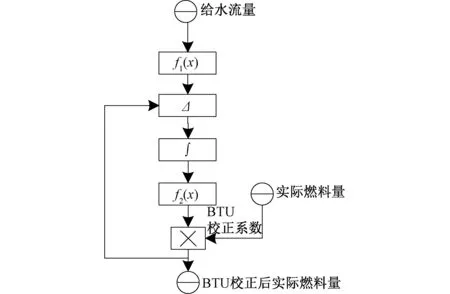
图1 常规BTU校正原理图Fig.1 Original BTU correction schematic diagram
文献[4]中燃料BTU实时校正方法将机组实际负荷N(MW)与基于机组负荷-压力模型得到的预测负荷值NS(MW)进行比较,其比值等于实际煤种发热量Qarj(MJ/kg)与设计煤种发热量Qars(MJ/kg)的比值,即为BTU校正系数KQ。
通过BTU校正系数得到的燃煤实际发热量可表示为
Qarj=KQ·Qars
(9)
当机组稳定运行时,实际发热量则可由上式(9)得到。
但由于燃煤燃烧过程需要时间,因此燃煤热值变化引起的炉内热量变化这一过程存在较大迟延,导致PID控制器中积分时间较长(通常为1 800~3 600 s)。这使得BTU校正回路只有在稳态工况下才具有实际意义,而当煤热值发生变化时具有较大动态误差。以下简称此方法为静态法
2.2 风氧量软测量法
火电机组中存在许多与热量相关的信号,与实际热量信号相关性最高且能快速反应热量变化的应取自燃烧过程中。文献[6]将锅炉风量和排烟氧量结合用于构造热量信号。
锅炉排烟氧量计算公式为
(10)

煤燃烧理论空气热量比为
(11)
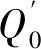
结合公式(11)、(12)风量,氧量和热量之间的关系为
O2=21(V-KvqQ0)/V
(12)
根据此式可计算出燃料的实际总发热量:
(13)
煤量惯性延迟信号uBD可表示为
uBD=uBe-40s
(14)
式中:uB为给煤量信号,t/h,延迟时间一般为40 s。
单位燃料发热量计算公式如式(15),该信号用Qard表示。
(15)
通过风量-氧量模型测得的煤发热量信号具有反应更快,惯性延迟更小的特点。原因是风氧量模型计算的热量相当于锅炉热平衡计算中输入锅炉的热量而不是机组有效吸热量,消除了热量转化为电能所需的一段时间,热量信号具有良好的动态特性。但由于Kvq的标定不准确,导致测量值不准确,静态误差较大。以下简称此方法为动态法。
3 基于卡尔曼滤波的燃煤发热量动 态软测量法
将由BTU校正和动态软测量法得到的两个在静态精度和动态特性上互补的信号,经卡尔曼滤波器预估—实测—校正过程后,得到一个动态精度高且静态输出稳定的信号,如图2所示[10-12]。
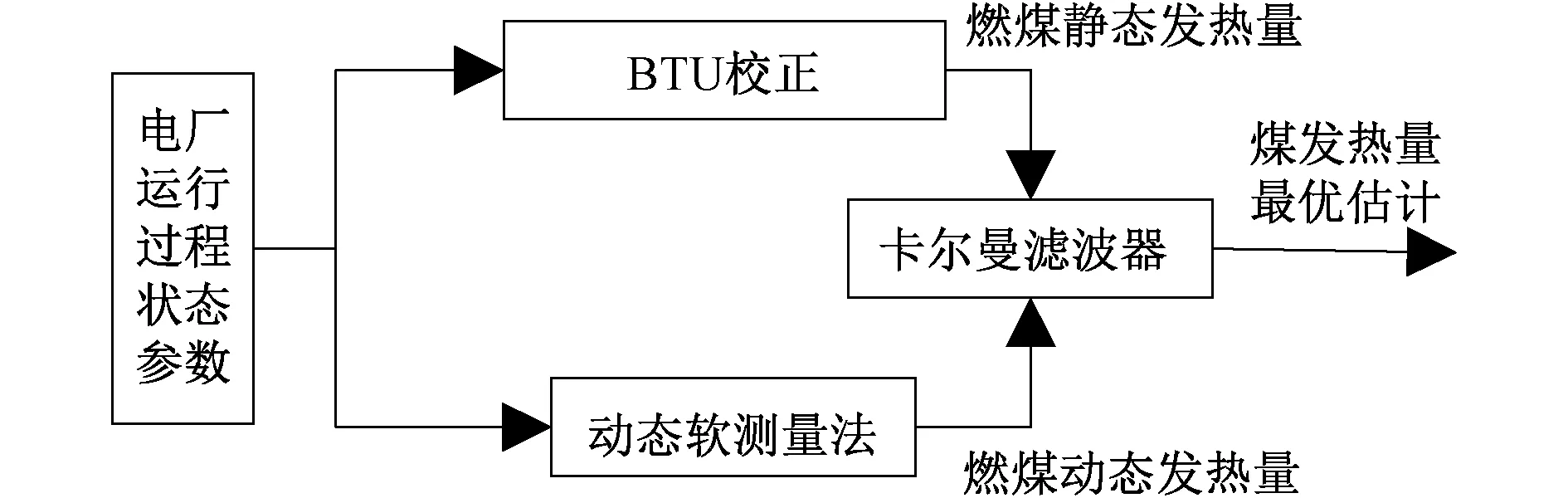
图2 卡尔曼滤波融合原理图Fig.2 Schematic diagram of Kalman filter fusion
由BTU校正得到一个燃煤发热量信号作为测量信号,记作Qarj(k)。该信号具有良好的静态特性,且其变化仅与煤质变化有关。由动态燃煤发热量软测量法得到另一个燃煤发热量信号作为状态信号,记作Qard(k)。该信号具有良好的动态特性。
构建该系统的状态方程和量测方程。
(16)
式中:Qard(k)和Qard(k-1)分别是k时刻和k-1时刻动态燃煤发热量软测量方法测得的煤发热量,w(k-1)为零均值高斯白噪声,其协方差为R1,z(k)为k时刻的测量值。Qarj(k)为k时刻BTU校正法得到的燃煤发热量值,v(k)为零均值高斯白噪声,其协方差为R2。
用k-1时刻的Qard信号值得到k时刻Qard信号的先验估计值。
Qard(k|k-1)=Qard(k-1)+w(k-1)
(17)
求出先验估计的协方差。
P(k|k-1)=P(k-1|k-1)+R1
(18)
式中:P(k|k-1)为先验估计的协方差,P(k-1|k-1)为k-1时刻状态最优估计协方差,计算保证k时刻的最优估计协方差P(k|k)最小的卡尔曼增益g(k)。
g(k)=P(k|k-1)/(P(k|k-1)+R2)
(19)
P(k|k)=(I-g(k))P(k|k-1)
(20)
将式(16)代入下式(18)中即可得到燃煤发热量的最优估计值Qard(k|k)。
(21)
在进行下一时刻的卡尔曼滤波时,令这一时刻的P(k|k)=P(k-1|k-1),Qard(k|k)=
Qard(k-1|k-1)代入即可。如此循环可得到每一时刻的卡尔曼滤波融合后的信号Qark,该信号能快速且准确的反应燃煤的发热量变化。
4 实验验证
针对调兵山电厂300 MW机组,锅炉型号SG-1065/17.5-M804,汽轮机型号NZK300—16.7/537/537,主要涉及参数示于表1。
(3)OLT向管理云上报ONT自动发现通知消息,包含ONT的所在OLT的框/槽/端口,以及ONT的SN。

表1 300 MW机组额定负荷设计参数
根据设计参数和扰动实验确定的机组额定负荷压力下简化的模型为[13,14]
(22)
(23)
3 100dpb/dt=-0.449ptμt+1.95rb
(24)
12dN/dt=-N+0.448ptμt
(25)
pt=pb-0.000 122 5rb1.5
(26)
由模型得到机组运行过程参数。其中汽轮机增益K3=0.449,制粉惯性时间Tf=330 s,制粉过程迟延时间τ=110 s,锅炉蓄热系数Cb=3 100。机组发电效率由机组发电-煤耗曲线确定[15,16]。
以某一段时间内电厂运行过程中的实时运行数据机组实际负荷N和基于负荷—压力模型得到的预测负荷值NS计算出BTU校正燃煤发热量。锅炉排烟氧量O2、进入锅炉的实际风量V计算出动态燃煤发热量。经过卡尔曼预估校正后的煤发热量值作为输出,用MATLAB搭建仿真模型。
观察图3、图4。在工况Ⅰ稳定高负荷运行状态下,煤发热量变化不大。静态法测得的数据波动较小数值稳定在17~17.5 MJ·Kg-1之间。卡尔曼滤波后数值非常接近由BTU校正计算出的煤发热量,误差不超过1 MJ·Kg-1。证明在此稳定工况下,卡尔曼滤波后的煤发热量比较准确。
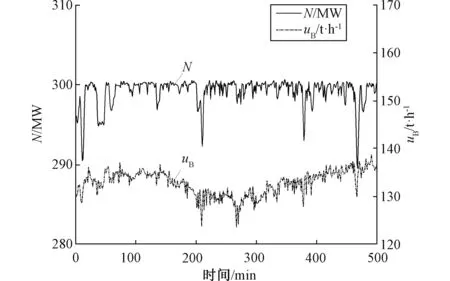
图3 工况Ⅰ运行历史数据图 Fig.3 Operation history data of power plant condition Ⅰ
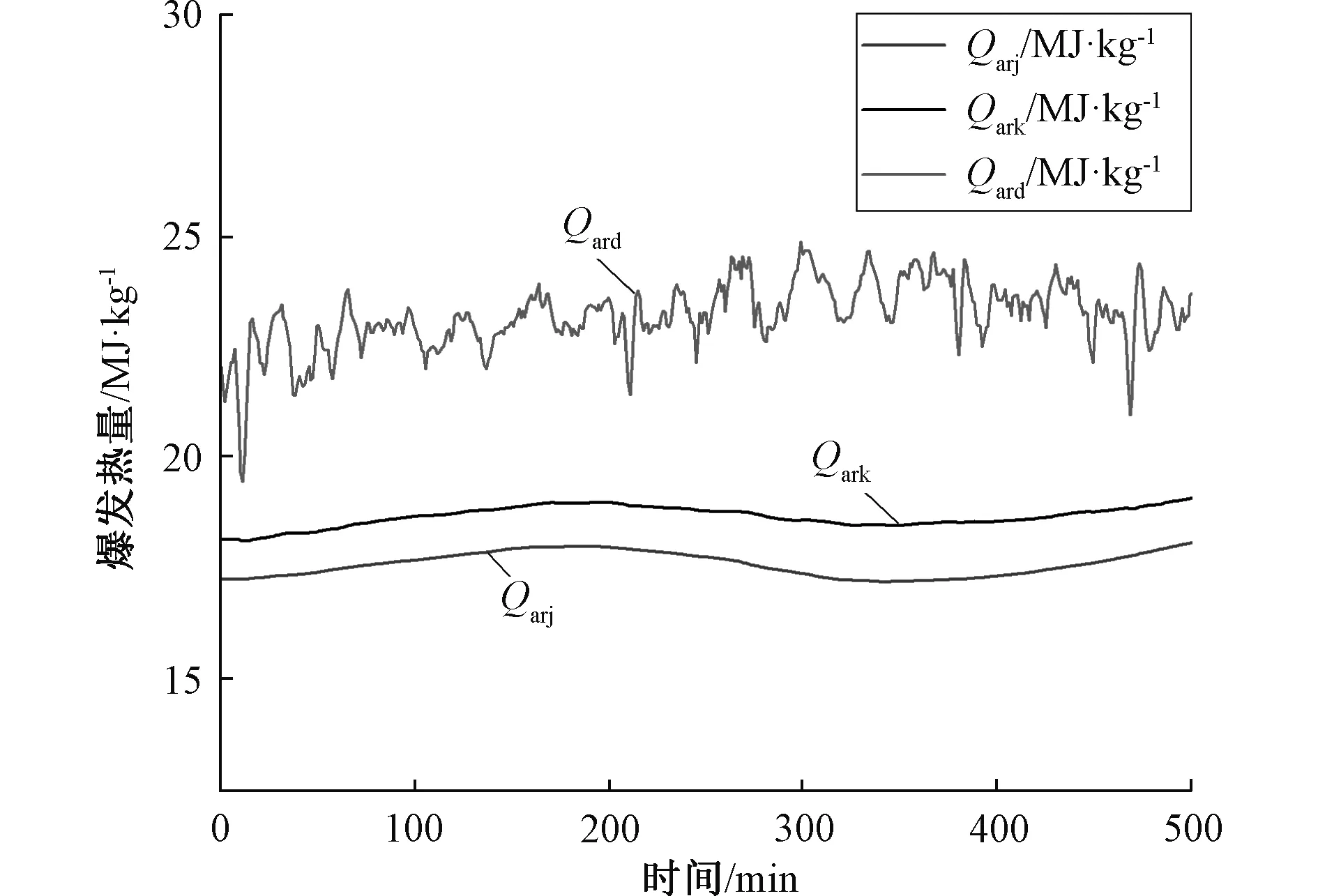
图4 煤发热量对比图Fig.4 Coal calorific values obtained by different method
当机组稳定运行,但给煤量发生改变。如图5、图6所示,机组负荷不变,给煤量持续增加。由BTU校正法测得的煤发热量波动不大,不能反映出此时煤发热量降低的趋势。相反动态法快速体现出了这种变化。卡尔曼滤波融合后的煤发热量既能快速反映出下降趋势且数值基于静态法而变化,波动范围在13~17 MJ·Kg-1间,提高了动态法的准确性。
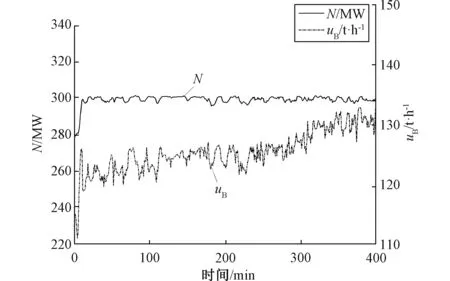
图5 工况Ⅱ运行历史数据图 Fig.5 Operation history data of power plant condition Ⅱ
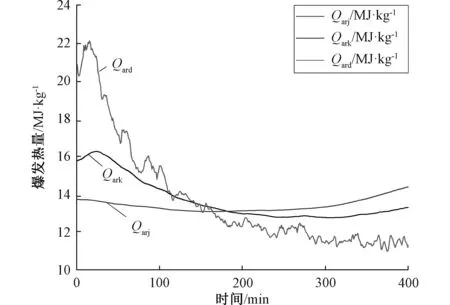
图6 煤发热量对比图Fig.6 Coal calorific values obtained by different methods
如图7、图8所示,当机组变负荷运行,此时煤发热量变化较小,在13~15 MJ·Kg-1内波动,煤动态发热量受机组变负荷的影响波动比较剧烈,上下浮动超过10 MJ·Kg-1。卡尔曼滤波融合后的煤发热量数值接近静态法煤发热量,且波动剧烈程度小,数值在14±1 MJ·Kg-1内,证明受动态法频繁变化的影响小。
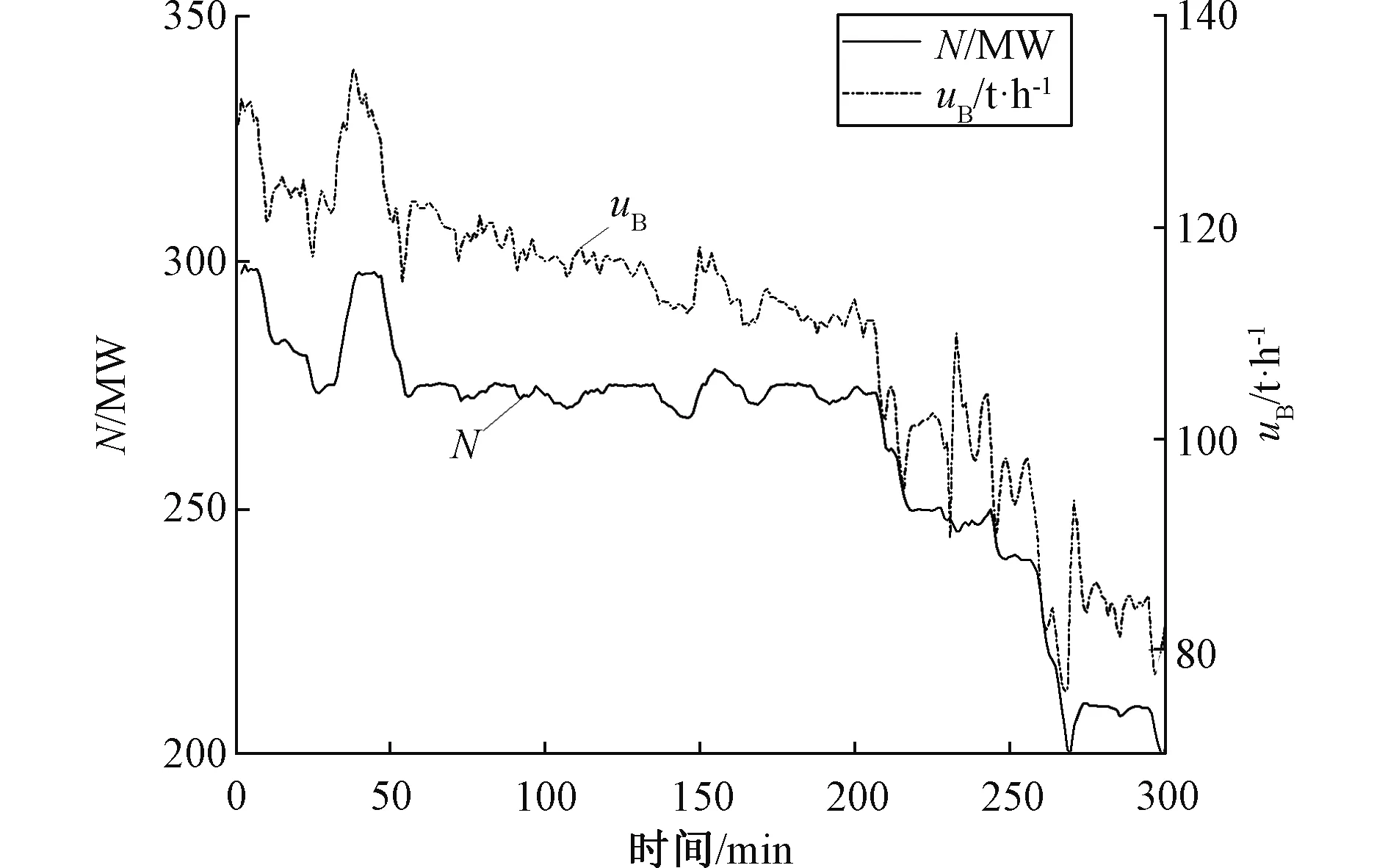
图7 工况Ⅲ运行历史数据图 Fig.7 Operation history data of power plant condition Ⅲ
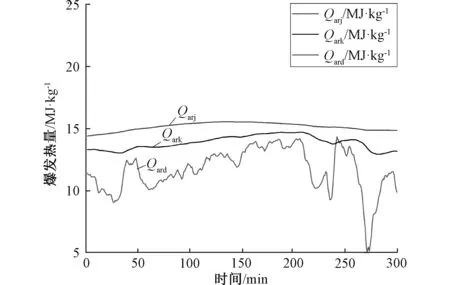
图8 煤发热量对比图 Fig.8 Coal calorific values obtained by different methods
工况Ⅳ如图9、图10所示,此时负荷降低50%,给煤量跟随下降。BTU校正法和动态法计算出的煤发热量先降后升。但相较于BTU校正法,动态法超前至少5 min反映出煤发热量变化,且在发热量变化期间更能体现出其快速微小的变动。卡尔曼滤波融合后,信号既能快速反映煤发热量变化,又能保证在数值上接近静态法计算结果(误差在4 MJ·Kg-1以内)。
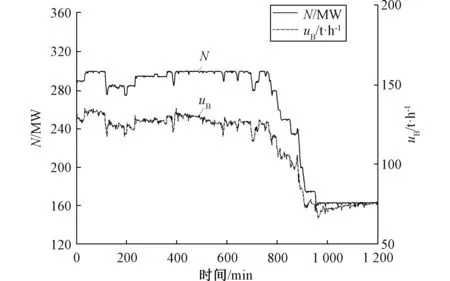
图9 工况Ⅳ运行历史数据图 Fig.9 Operation history data of power plant conditionⅣ
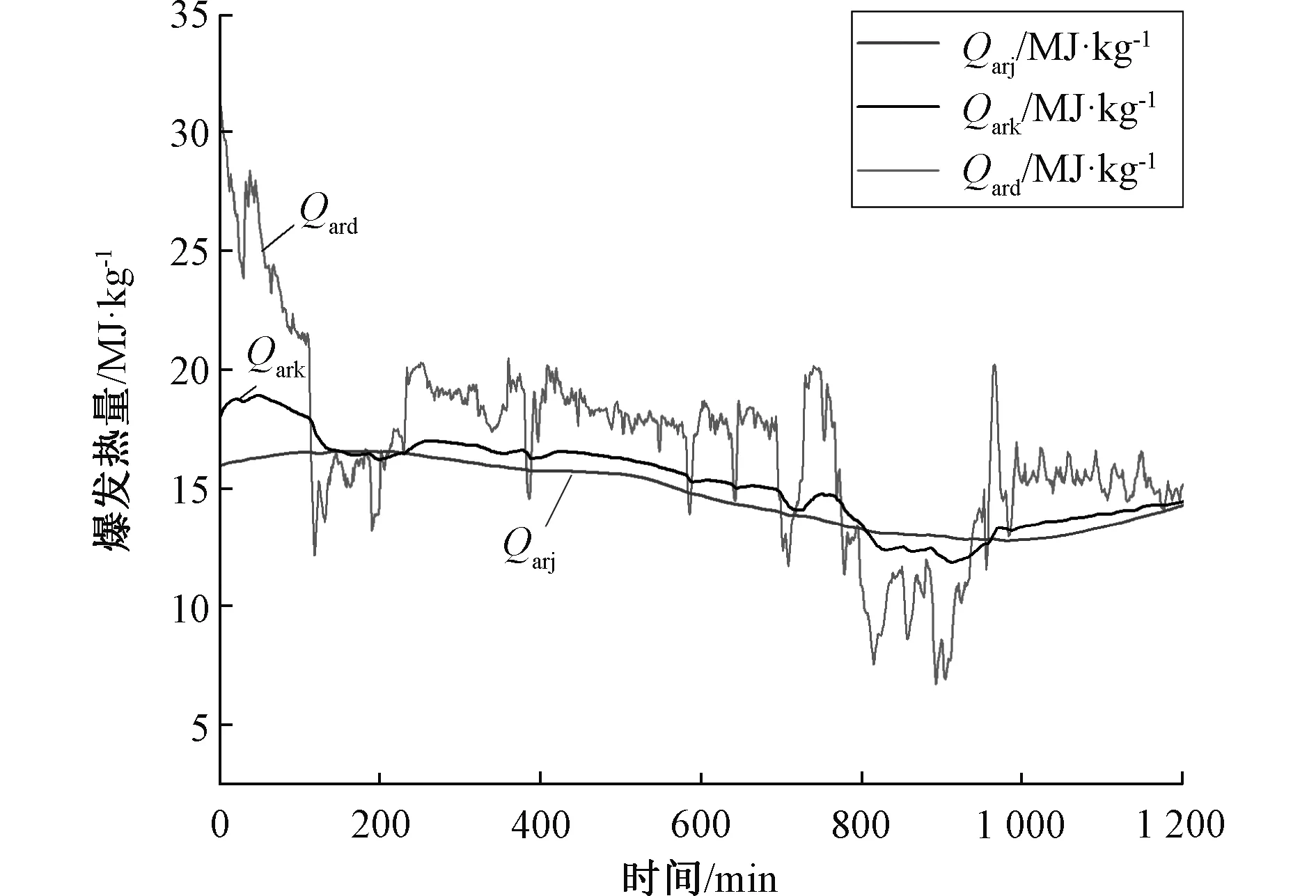
图10 煤发热量对比图Fig.10 Coal calorific values obtained by different methods
对三种方法所得结果进行数据分析。表2是在变负荷燃煤发热量稳定时采样,此时静态法的结果相对准确并以此为基准。相较于动态法发热量均值,融合后发热量均值与静态发热量均值更接近,精度提升5%,证明其准确性。从方差可以看出,融合后发热量方差0.3<动态法发热量方差3.1且非常接近于静态法发热量方差0.1,证明发热量变化较小,与此时煤发热量稳定情况相符合。
表3是在负荷稳定燃煤发热量变化时采样,热值相对变化量是变化的发热量减去稳态发热量初值,代表某一时刻的动态偏差。计算得出动态法相对变化量最大,符合此时燃煤发热量不稳定情况,但变化范围10.43,数值变动幅度过大,反映出数值不准确的问题。滤波融合后热值相对变化量均值是2.67 MJ·kg-1变化范围3.52,大于静态法热值相对变化量均值0.28 MJ·kg-1,小于动态法变化范围10.43。相对静态法反映发热量变化的程度增加21%,表示滤波融合后既能够体现发热量变化,又能保持数值准确度。
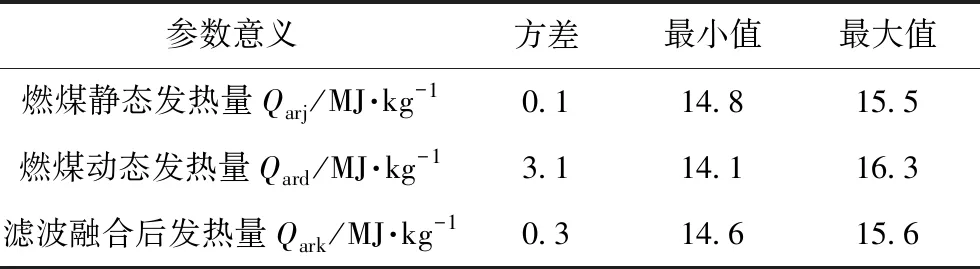
表2 变负荷燃煤发热量稳定时数据分析
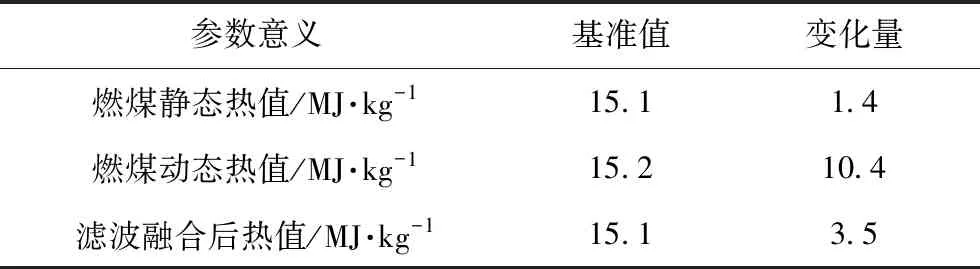
表3 负荷稳定燃煤发热量变化时数据分析
5 结 论
以卡尔曼滤波原理为基础,对BTU校正测得的煤发热量与风氧量模型计算出的燃煤发热量进行了融合,得到了既有好的动态特性又有静态准确性的煤发热量信号,并对该测量燃煤发热量方法进行验证。用MATLAB进行仿真,得到以下结论:
(1)在机组稳定高负荷运行情况下,利用卡尔曼滤波融合得到的燃煤发热量信号能反映煤的发热量变化。当煤发热量变化小时,数值接近BTU校正法计算值,体现出其静态精度高的特点。
(2)在机组运行不稳定时,融合后的燃煤发热量具有良好的动态特性,能够快速反映煤发热量的变化且滤除了动态法中的高频噪声。使计算结果更加稳定。
(3)本方法能够兼顾软测量的快速性和准确性,相对于动态法变负荷工况动态误差减小15%以上,相对静态法反映速度提升10 min以上,用于BTU校正时补偿量提高20%以上,具有很好的工程应用价值。
