基于编码解码思想的鬼波预测与压制方法
2021-04-07王永强王华忠孙维蔷胡英张才
王永强, 王华忠*, 孙维蔷, 胡英, 张才
1 同济大学海洋与地球科学学院波现象与智能反演成像研究组, 上海 200092 2 中国石油勘探开发研究院, 北京 100083
0 引言
高分辨率勘探是最近几年海上油气地震勘探的热点问题,鬼波压制是其中的核心议题.众所周知,海上地震资料采集过程中,为避免复杂海水表面因素的影响,需将震源与接收器置于海水表面以下某一深度.由于海水与空气的接触面是一良好的反射界面(反射系数近似等于-1),来自地下反射界面的反射波场在到达接收器(形成检端上行波场)后,还将继续向上传播,并经海水表面向下反射,再一次被接收器接收到,形成检端下行波场,即检端鬼波波场;同样,震源激发波场,除了下行传播的波场(这部分是正常的下行波场),还有向上传播的波场,经海水表面向下反射,形成源端鬼波波场.可见以震源点和检波点位置为参考点,源端的上行波场与下行波场、检端的上行波场与下行波场,两两组合即形成最终的记录波场,它是无鬼波波场、源鬼波波场、检鬼波波场以及源检鬼波波场的叠加.
鬼波对地震资料处理的影响可归纳为如下四点:1)鬼波的拖尾效应,使得地震子波变胖,进而降低成像分辨率;2)鬼波的陷波效应,损害有效频带,尤其低频端信息缺失,影响FWI等;3)鬼波的时延空变效应,使得地震子波的动力学特征失真,影响后续的AVA/AVO反演等;4)鬼波的行波方向效应,扰乱SRME等自由表面多次波压制方法.因此,鬼波压制现已成为海上地震勘探的重点研究问题,目的是尽可能提取出无鬼波波场,压制鬼波波场影响,恢复地震数据宽频带、高分辨率的特性.
鬼波压制的基本思想主要体现在采集和处理两个阶段.采集阶段是通过设计观测方式控制陷波点分布.因此,鬼波压制方法总是与采集系统紧密地关联在一起,其基本思想是通过改变采集模式以引入陷波频率的多样性,进而得到更为稳健的等效去鬼波算子.Ozdemir等(2008)探索并发展了上、下拖缆采集压制鬼波的思路,即将两条拖缆置于两个不同的深度同时进行数据采集,进而引入两套不同的陷波频率特性;Barr和Sanders(1989),Starr(1998),Carlson等(2007)等提出在拖缆上同时安置水检与陆检.由于压力分量与速度垂直分量具有不同的行波方向响应特性,因此也就引入了两套不同的陷波频率特性;Soubaras等(2010,2012)则进一步扩大了宽频采集的范畴,提出了变深拖缆采集(VDS),即水检深度随偏移距的不同而不同.虽然宽频采集能够得到更为稳健的去鬼波效果(得益于等效去鬼波算子的稳健性),但由于其对采集系统的工程要求更高,成本更高,因此仅在某些特定的区块得到了应用.不同的采集方式,具有不同的陷波频率分布特征,对应地发展了不同的去鬼波方法.处理阶段是通过提出更好的鬼波预测算子,并在合适的反演框架下,估计一次波场,实现鬼波与一次波的分离.这样的方法主要是针对常规的水平缆采集的数据体,例如Fokkema和 Van den Berg(1993)最早给出的频率-波数域波场外推法去鬼波方法;Weglein等(1997)理论上推导出了全波场域压制鬼波的逆散射级数法,王芳芳等(2013)则对该方法进行了实现;Wang和Peng(2012)在频率-波数域波场外推的基础上进一步发展了寻优水检深度的Bootstrap方法,Wang等(2013)则将其又扩展到了频率-射线参数域.上述针对水平单缆的鬼波压制方法虽然能够在实际资料处理中取得一定效果,但由于预测和压制被融合在一个滤波器中,限制了对鬼波的预测能力和压制能力.
鬼波压制方法优劣的判断标准:①鬼波在什么阶段压制?最好在采集阶段压制,不要留到处理阶段.②鬼波压制方法的假设条件是什么?假设条件越松越好.③鬼波压制方法的保真程度如何?对一次波的保真度越高越好.
到目前为止,没有办法证明宽频采集的鬼波压制方法更有优越性,而且宽频采集压制鬼波方法之间孰优孰劣也无法证明.在处理阶段发展更全面的鬼波预测算子,在一个更好的反演框架下进行更彻底的鬼波与一次波的分离还是非常必要的.
由于常规水平单缆采集应用广泛,与之配套的后续处理流程发展成熟,且由于其采集成本更低,因此在可预见的将来,常规水平缆采集依然举足轻重.这也就决定了针对常规水平缆鬼波压制方法的研究仍然需要引起足够的重视.因此,本文聚焦于常规水平缆所采集数据的鬼波压制算法的研究.本文基于编码与解码理论框架,用编码建立起鬼波预测模型(相当于正问题),在Bayes反演框架下建立起解码估计一次波、去除鬼波的方法(相当于反问题).正问题准确性决定了反演的效果.本文采用的编码鬼波预测模型中可以考虑到影响鬼波压制的各种因素,譬如源、检深度的不准确、海水表面不水平、甚至海水表面反射系数的空变等,基于此模型及相应反演理论的鬼波压制得更为彻底.实际上,本文提出的编码鬼波预测模型并非局限于水平缆观测的情形.实际资料处理验证了编码与解码框架下鬼波压制方法的可行性与有效性.
1 方法原理
1.1 编码理论下鬼波预测器的构建
编码与解码方法在信息科学领域中有广泛应用.鸡尾酒会问题是典型的例子(Ikelle, 2007,2010).麦克风接收并放大来自不同嘉宾的语音信号,这个过程可以理解为不同语音信号的“编码(encoding)”过程.从混叠语音信号中分辨出感兴趣的嘉宾的声音可以理解为对混叠语音信号的“解码(decoding)”.如忽略音色等特征,解码过程往往是异常困难的,因为麦克风对不同语音信号的编码机制(编码算子)是未知且复杂的,而音色等特征可以认为是对混叠前语音信号的先验信息,基于此先验信息,能够从混叠语音信号中分辨出感兴趣的嘉宾的声音.
编码前独立信号、编码算子(取决于具体物理问题)与实测的混叠信号三者构成编码与解码理论的基本元素.其中编码是正问题,目的是预测实测数据;解码是反问题,目的是估计独立信号或同时估计独立信号和编码算子.同时估计信号和编码算子的问题又称为盲源分解问题.
勘探地震中很多问题可以提为编码与解码问题,譬如随机同时源激发、接收以及混叠数据的分离,水体相关多次波(甚至层间多次波)的预测与压制问题.鬼波预测与压制同样可以类比为一个编码与解码问题.和鸡尾酒会问题类似,对检鬼波而言,水检为麦克风,记录到的波场为混叠语音信号,而上行波场则为混叠前独立语音信号,编码算子可以理解为上行波离开水检传到海面再返回到水检的整个传播过程.源鬼波和源检鬼波可同样解释.相比于传统的鬼波预测方法,此处的编码算子(至少原则上)可以考虑诸如缆深不准确,水体速度变化,水体表面反射系数空变等因素的影响,实现对鬼波的更为精确的预测.用编码和解码理论来解释鬼波预测与压制方法的好处是这样的思维方式有一个明确的正问题和反问题架构,可以借用目前的各种编码算子提炼正问题,反问题的框架更为明确,即Bayes反演框架.在这样的框架下处理问题包容性很广,正问题可以提得更符合实际;反问题可以考虑更合理的正则化方法.
正问题是反问题的基础,正问题对实测数据(即物理过程)的预测越准确,反问题的求解精度越高.
如图1所示,第j道水检记录到的下行检鬼波可以看作为来自地下不同反射界面上行波场的混叠,它们对应于不同的入射角度.而对于某一特定的入射角度θk,可以看作为第k道水检(作为编码道)记录到的上行波场继续向上传播,经海水表面下行反射到达第j道水检产生对应的鬼波成分.任何角度的上行波到达水面并被反射到第j道水检产生的鬼波都可以这样理解.可以把第j道水检视为上述麦克风,传播算子视为编码算子,无鬼波上行波场是上述编码前独立信号.这就是鬼波预测提为编码问题的原因.当然也可以用任何类似的框架来解释鬼波的产生.
假设海水表面为理想的镜面反射,第j道水检记录到的下行波场可以通过沿拖缆方向对各个水检记录到的上行波场进行如图1所示的编码得到.在频率-射线参数域,编码过程可以描述为
(1)
Xj(ω,pk)=Uj(ω,pk)+Dj(ω,pk),
(2)
其中,Dj(ω,pk)为第j道记录到的入射角度θk满足sinθk=vpk的下行检鬼波;Ui(ω,pk)为第i道记录到的具有相同入射角度的上行波场;r·e-iω tpkAji为对应Ui(ω,pk)与Dj(ω,pk)的编码算子,即连接起拖缆数据中第i道处上行波与第j道处的下行波的Green函数,其中,r为水面反射系数,tpk为取决于入射角度、缆深和水速的走时差,Aji为编码系数中的权重项,即使用当前Green函数路径与理想反射路径的吻合概率当前编码项进行加权;Xj(ω,pk)为第j道记录到的原始波场,N为沿拖缆方向分布的水检道数.
考虑到沿拖缆方向的所有水检,则式(1)与式(2)可以表示为如下矩阵形式:
(3)
上式进一步简化得到,
X=LU,
(4)
其中,X为混叠记录波场,其中同时包含有检端上行波场与下行波场;L为编码矩阵,亦称之为编码算子;U为解码后得到的上行波场(即去除检鬼波后的上行波场).X、L与U构成编码与解码框架下检鬼波压制理论的三个要素.公式(3)有较高的抽象性,能统一地对多种观测方式(如水平缆、变深缆等)进行建模,式中tpk与Akj根据具体观测方式有不同形式,将在下一节讨论.
公式(3)和(4)的物理解释是海上拖缆记录到的观测数据是对传播到检波点处的上行波场进行编码得到的,其中上行波继续到达海水表面再下行反射至检波器的Green函数构成编码算子(它取决于海水表面反射系数r、编码系数Akj以及记录道与编码道的走时差异tpk).公式(3)和(4)建立起了线性正问题,即一次上行波和实测含鬼波数据的之间的预测关系.
1.2 Bayes框架下最优反演方法压制鬼波
上节所表述的预测正问题,具有高度抽象性,能统一地建模多种观测方式.为了方便分析问题,此处将具体讨论常深度水平拖缆情形.如图1,假若海水表面为理想的镜面反射(反射系数r已知),海水速度v以及拖缆深度d已知,则对应于某一入射角度θk,其编码算子中的待定项Aji,tpk有如下表达:
(5)
(6)
其中,δ表示关于理想鬼波反射路径的最大容许偏差;此时,公式(3)(4)所表述的正问题中的编码算子被具体化为一个带状对角阵.
解码问题一般地可以定位为Bayes框架下的参数估计问题.Bayes框架的引入可以清楚地解释反问题的本质,尤其对正则化思想与方法在提高反演精度中的重要性有深刻的说明.此处,并不详述Bayes估计理论,而是直接切入泛函优化问题.
在Bayes框架下建立如下目标泛函,
(7)
求解该优化问题可以实现对上行波场U(无鬼波波场)的最优解码.其中,λ是衡量数据残差与模型残差的权重;P代表不同的范数.在频率-射线参数域求解公式(7),去鬼波后的上行波场应该存在稀疏性,进行稀疏约束反演(P=1)是合适的选择.此时,公式(7)是一个“L2数据匹配项+L1正则化项”的优化问题,可使用次梯度方法.其迭代解可表达为
Uk+1=Γα λ[Uk-αLH(LUk-X)],
(8)
其中,Uk-αLH(LUk-X)是一次常规的梯度更新;α表示梯度更新的步长;Γβ[·]是一个L1阈值收缩算子,β是其收缩步长.关于梯度步长与L1阈值收缩算子具体形式,详见附录A.
从公式(8)可见,本算法的主要迭代过程是在沿负梯度反向更新的结果上进行一次L1阈值收缩.因此,它的总体计算量与梯度类算法相当,并没有引入额外的计算成本.
1.3 实际资料中的不确定性
实际上,在处理海上地震资料时,存在着诸多不确定因素可能影响最终的解码效果.例如,海水表面并非理想的镜面反射,此时记录道与编码道之间的一一对应关系就会脱离入射角度的制约,且海水表面反射系数也不再是-1;海水速度随温度、盐度、拖缆深度、季节性洋流等发生变化,而不再是一个常数;海况复杂,且拖缆控制系统存在误差等也会使得真实的水检深度并非预设的深度值,等等.如图2—4所示,以1D情形为例,这里分别给出海水速度不准确、水检深度不准确以及海水表面反射系数不准确等对最终解码效果的影响.可以看到,这些因素的错误估计都会进一步产生并放大Ringing噪声,且估计误差越大,Ringing噪声越发育.

图1 编码上行波场得到下行检鬼波示意图(a) 单个检波点接受到的鬼波; (b) 单方向鬼波的传播示意图.Fig.1 Sketch of down-going receiver ghost by encoding the up-going wavefield(a) The ghost received by a single detection point; (b) The propagation diagram of the ghost of one direction.
通常情况下,海上地震资料实时采集时,海水盐度、温度等参数都会被记录得到,其目的是减小海水速度估计误差,也因此,海水速度参数对实际地震资料解码影响是比较小的.至于海水表面反射系数,这里给出一经验公式以弱化实际海水表面反射系数对解码的影响,即综合考虑海水表面起伏、入射角度、频率等因素的影响:
(9)
其中r0为参考反射系数,一般取值为-0.97;σ为海水表面波浪的起伏高度.从表达式可以看出,当入射角度与浪高固定时,海水表面反射系数随频率的增高而减小;当频率与浪高固定时,海水表面反射系数随入射角度的增大而增大;当频率与入射角度固定时,海水表面反射系数随波浪起伏增大而减小.进一步地,至于缆深因素的影响,由于其实际发生扰动的深度范围是有限的(一般为±2 m),因此可以在当前计算数据窗口内按照给定的深度范围(d-2)~(d+2),对当前炮,通过建立如下目标泛函,实现拖缆深度的最优估计:

图2 拖缆(水检)深度对解码结果的影响(1D) Fig.2 The influence of receiver depths on the deghosting result (1D)
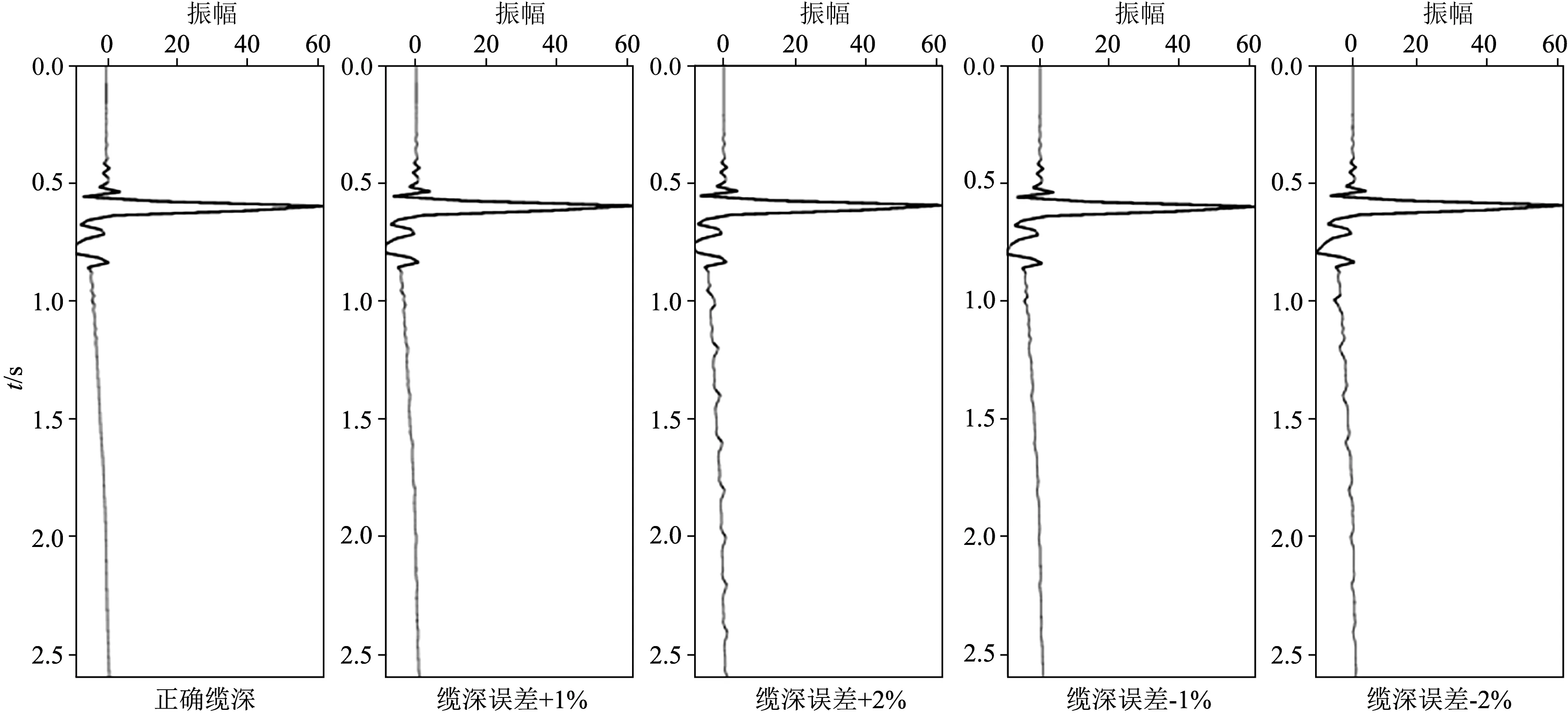
图3 反射系数对解码结果的影响(1D)Fig.3 The influence of reflectivity on the deghosting result (1D)
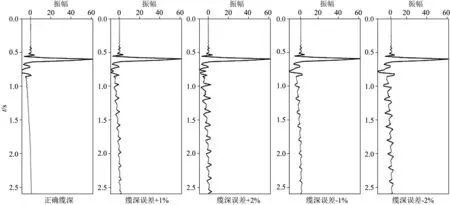
图4 海水速度对解码结果的影响(1D)Fig.4 The influence of water velocity on the deghosting result (1D)
(10)
其中,Ude和Dde分别对应基于某一缆深解码得到的检端上行波场与下行波场.上式的物理含义是,当缆深对应于实际拖缆深度时,原始观测数据与解码得到的检端上行波场与下行波场(检鬼波)的差异为最小,此时Ringing噪声的能量势必也是最弱的;相反,若拖缆深度不准确,误差则会增大,对应.此时Ringing噪声的能量也会增强.图5对应1D情形不同水检深度值时,式(9)对应的误差曲线.可以看到,当水检深度为真实深度值15 m时,原始观测数据与解码得到的检端上行波场与下行波场(检鬼波)的差异达到最小.
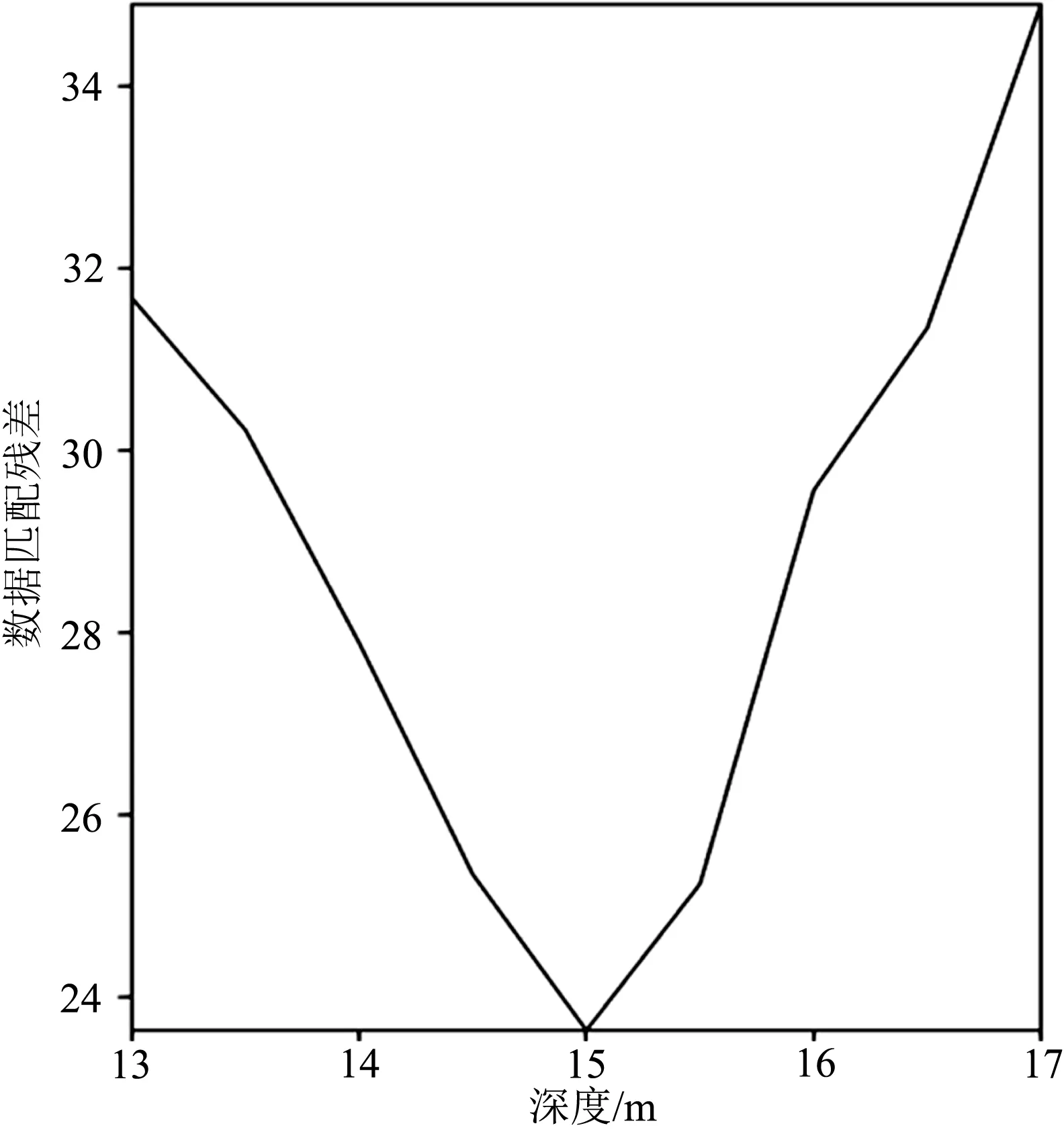
图5 不同拖缆(水检)深度对应的数据匹配残差曲线Fig.5 The curve of data matching residuals due to different receiver depths
2 数值试验
为验证本文方法的有效性,首先对sigsbee2a模型的合成数据进行了测试.实验中施加自由表面边界条件,使得有限差分正演模拟出鬼波反射.在该模型中,盐丘边界的强反射率和盐丘的陡峭角度带来了额外的挑战.
由于自由表面边界条件下的正演模拟的炮集数据被鬼波污染(图6a),原始的RTM成像结果呈现较低分辨率,尤其是在盐丘的边界处(见图7a箭头处).用本文方法去鬼波后的炮检记录(见图6b)中没有鬼反射,反射同相轴的子波波形变得更尖锐.最后,从去鬼波后的炮集数据的RTM成像结果(见7b)在分辨率上有了显著的提高.盐丘的边缘变得清晰,验证了本文方法的有效性.
为进一步验证上述编码与解码框架下检鬼波压制方法的有效性,这里以南海某一探区2D地震资料为例.由于该区块地质环境复杂,尤其微构造、微断层等发育,因此高精度高分辨率的地震成像是关键,进而数据预处理阶段有效的鬼波压制算法举足轻重.该2D水平拖缆数据,炮点间隔75 m,水检间隔12.5 m,单道记录长度12.288 s,采样间隔4 ms.拖缆预设深度为10 m,炮点深度6 m.这里仅考虑检鬼波的压制,源鬼波暂且不予考虑.图8a为原始单炮道集:同时包含检端上行波场与下行检鬼波;图9a为对应方框的局部波形图,如箭头所示,两者极性相反,检鬼波犹如尾巴般紧紧跟在上行波之后,进而使得地震子波变胖,影响后续的成像分辨率.按照给定的目标泛函(式(9)),在8~12 m深度范围内,寻优当前计算窗口(窗口大小为30道)内的拖缆深度,并考虑到海水表面反射系数的影响,图8b为最终解码得到的上行波场,从局部放大波形图9b中可以看到,拖曳着的检鬼波得到显著压制.图8c为考虑到拖缆深度因素,但未考虑到海水表面因素的解码结果,从其局部波形图9c相较于9b对比来看,检鬼波依然有些许残留.图8d与9d为既未考虑海水表面因素,也未考虑拖缆深度因素的解码结果,解码效果更为糟糕,检鬼波还有很强烈的残留.图8e与9e则对应于传统的频率-波数域波场外推法鬼波压制结果,即使考虑到海水表面因素与拖缆深度因素,压制效果依然不尽人如意,检鬼波依然有残留.图10给出了振幅谱对比图,其中圆点线代表包含检鬼波的原始记录波场,实线代表最终解码得到的上行波场:无论是低频端还是高频端能量都得到提升,频带变宽.
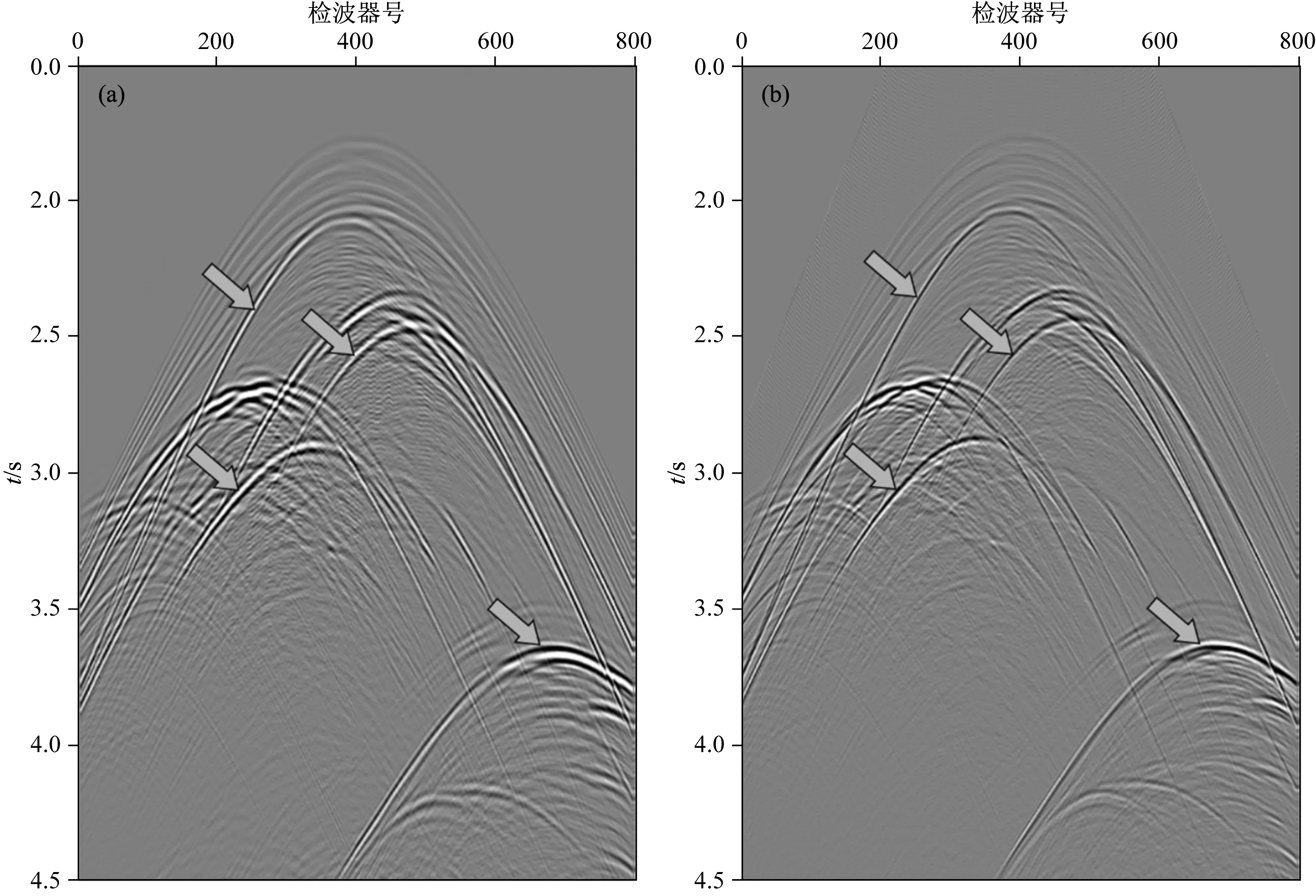
图6 sigsbee2a模型算例中的一个共炮道集去鬼波前后对比(a) 原始; (b) 去鬼波后.Fig.6 Comparison of a common shot gather in sigsbee2a synthetic example before and after ghost removal(a) Original; (b) After ghost wave removal.
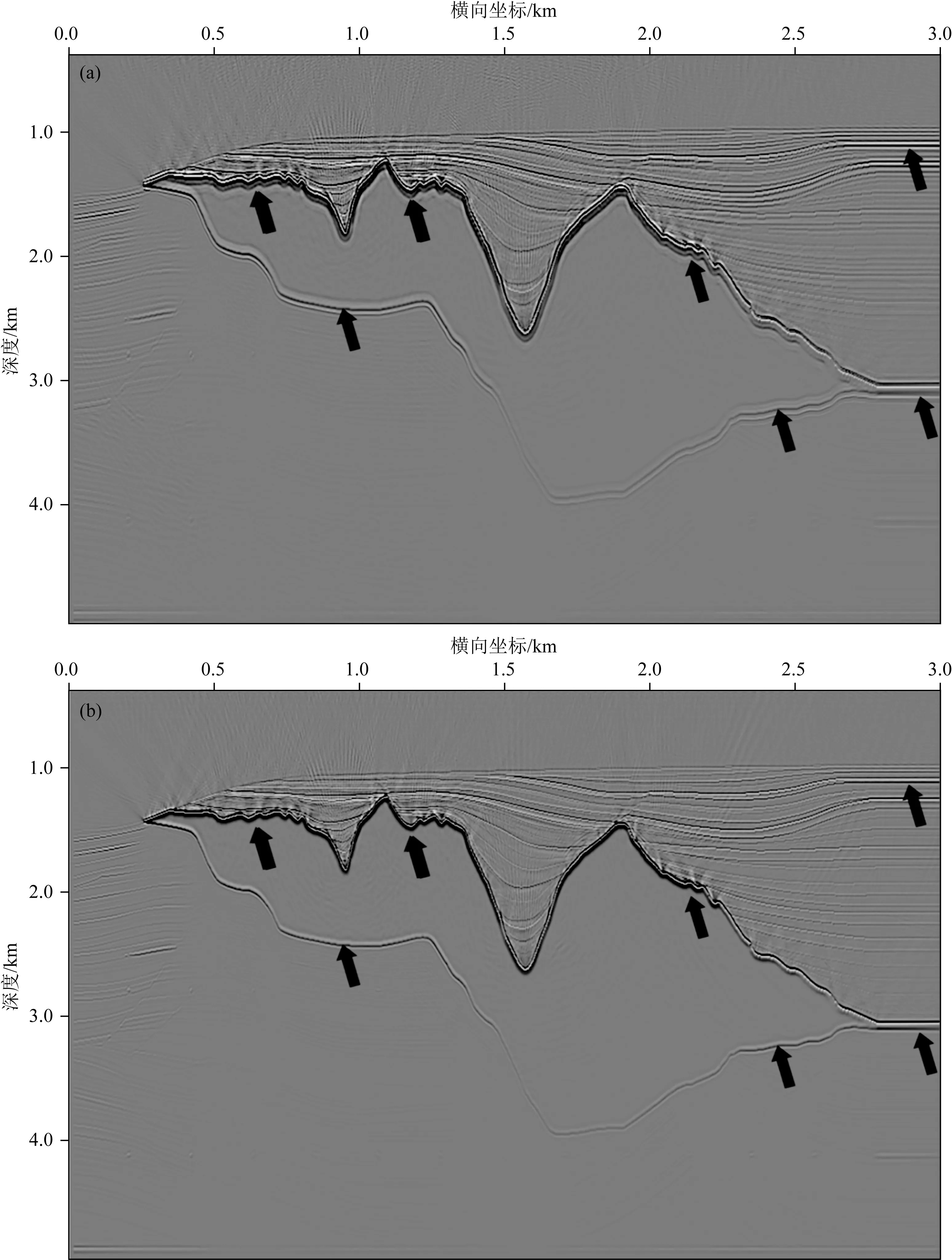
图7 sigsbee2a模型算例中的RTM成像结果去鬼波前后对比(a) 原始; (b) 去鬼波后.Fig.7 Comparison of RTM result in sigsbee2a synthetic example before and after ghost removal(a) Original; (b) After ghost wave removal.

图8 (a) 原始单炮道集; (b) 考虑到拖缆深度与海水表面因素的解码炮道集; (c) 考虑到拖缆深度但未考虑海水表面因素的解码炮道集; (d) 既未考虑拖缆深度也未考虑海水表面因素的解码炮道集; (e) 常规F-K域波场外推法去鬼波炮道集Fig.8 (a) The original shot; (b) The deghosting shot considering the receiver depth and sea-surface condition; (c) The deghosting shot considering the receiver depth but not the sea-surface condition; (d) The deghosting shot neither considering receiver depth nor sea-surface condition; (e) The traditional deghosting shot

图9 分别对应于图8中方框所圈定的局部放大波形图Fig.9 The partial enlarged views corresponding to Fig.8
编码与解码框架下去除检鬼波之后,基于SRME消除自由表面多次波.对分离出的上行一次反射波进行RTM成像,并比较检鬼波压制前后成像剖面的改善.图11、图12、图13分别对应该勘探区域浅层、中层、深层某一区块.图11a、图12a、图13a对应检鬼波压制前成像剖面,其中箭头指示拖曳着的检鬼波,可以看到同相轴变胖,成像分辨率显著降低.图11b、图12b、图13b则分别对应检鬼波压制后的成像剖面,很明显,拖曳着的检鬼波被压制掉,成像同相轴明显得到恢复.进一步地,图14(a,b,c)分别对应浅层、中层、深层检鬼波压制前后的振幅谱对比.不难看出,检鬼波压制后,低频端能量得到恢复,频带得到了拓宽.
3 讨论
鬼波是海上地震勘探的常见干扰.该现象的成因是位于水下的检波器,在接受上行反射波的同时,也会受到来自水面的下行波的干扰,因此该现象可类比于“鸡尾酒会问题”.在“编码-解码”框架下,可将来自不同演讲者的语音分离;同理,在“编码-解码”框架下,也可将来自不同方向的入射波分离.相比于传统的ω-p域鬼波预测算子,本文“编码”虽然具有等价的数学描述,但侧重于不同方位、不同来源的信号混叠过程.因此在该角度下,运用Bayes反演理论,可解码得到来自不同方向的波场.
对于实际情况下的缆深、水速、海面反射系数不确定性,本文分别测试了这些因素的误差影响.这些因素实际上导致正算子不准确,本文并通过引入Bayes反演框架,本身可在一定程度上容许正算子的误差,从而缓解了对精确缆深、水速、反射系数的要求.
本文虽然仅仅讨论了常深度水平拖缆情况.对于更复杂的变深度拖缆,编码矩阵L中Aij、tpk等元素的计算需要考虑各个检波点的实际坐标,从而使得编码矩阵形式上更为复杂.但对于反问题的解码过程,并没有引入额外的难点.
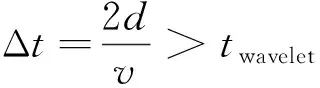
本文主要讨论检端鬼波,但本文的算法不仅仅局限于检波端鬼波,对于源端鬼波、源检鬼波也同样能够处理.源端鬼波主要问题是空间样点稀疏,在炮点采样满足采样定理的假设下,本算法也适用于源端鬼波;当炮点过于稀疏时,需要对数据进行加密插值,才能使用本算法.顺序地施加本算法于“共炮道集”、“共检波点”道集之后,即可消除数据中的三种鬼波.
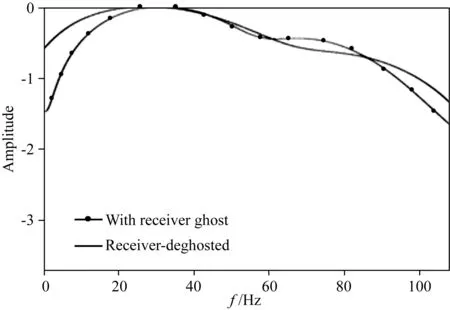
图10 解码(去检鬼波)前后地震数据振幅谱曲线对比Fig.10 Comparison of amplitudes pectrums before and after deghosting
4 结论
宽带、宽方位(长偏移距)和高密度采集及对应的成像处理是油气地震勘探的正确技术方向.海上宽带地震勘探表现为宽带采集技术及相应的去鬼波技术,核心问题就是压制鬼波.气枪震源的扩频是另一个问题.宽带地震勘探的优点已经得到了充分的证明.
数据处理阶段的鬼波压制本质上涉及到鬼波预测问题(正问题)和鬼波与一次波分离问题(反问题),而且鬼波的精确预测是更关键的.我们从编码的角度考虑鬼波与一次波的关系问题,构建出了更为精确的鬼波预测模型,其中可以包括缆深、水速、水面非水平,甚至水面反射系数空变等.在Bayes框架下构建了估计去鬼波后上行波场的方法(即解码方法).在Bayes框架下可以方便地考虑稀疏约束反演类的正则化方法,可以考虑进行盲反演,也可以视情况考虑多参数反演.我们仅给出了针对常规水平拖缆的编码与解码框架下检鬼波预测和反演压制公式,实质上该框架既并不限于平缆、也不限于检鬼波,它可以方便地处理任意缆形、源鬼波和源检鬼波.
我们相信,在所提出的编码预测器基础上,基于非高斯反演框架的鬼波压制方法会有更好的效果,这是今后我们希望探索研究的.
致谢感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中石化物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持.

图11 勘探区域浅层(a) 去除检鬼波前; (b) 去除检鬼波后.Fig.11 The shallow exploration area(a) Before deghosting; (b) After deghosting.

图12 勘探区域中层(a) 去除检鬼波前; (b) 去除检鬼波后.Fig.12 The medium-deep exploration area(a) Before deghosting; (b) After deghosting.
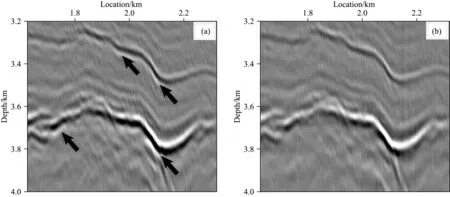
图13 勘探区域深层(a) 去除检鬼波前; (b) 去除检鬼波后.Fig.13 The deep exploration area(a) Before deghosting; (b) After deghosting.

图14 (a)、(b)与(c)分别对应于浅、中、深层成像剖面去鬼波前后振幅谱对比曲线Fig.14 Comparison of amplitude spetrums before and after deghosting corresponding to Fig.11,Fig.12,Fig.13
附录A
公式(8)中的梯度步长α可由梯度方向上的一维搜索求得,其形式可表达如下:
式中,p是当前梯度方向.
软阈值收缩算子Γβ的具体形式如下:
Γβ[x]=sgn(x)·max{|x|-β,0}
其中,β是收缩步长;sgn表示符号函数,即取变量的正负号,对于复变量则为取相位.
