基于模糊强化学习的双轮机器人姿态平衡控制

闫 安, 陈 章, 董朝阳, 何康辉

(1.北京航空航天大学航空科学与工程学院, 北京 100191;2.清华大学自动化系, 北京 100084)

0 引 言

单轨双轮机器人因其高度的平稳性、较强的越障能力等性能在生活服务型机器人中表现出其强大的优势,可以广泛应用于军事、交通、安保、工业生产等领域。同时,与倒立摆系统类似,双轮机器人有多变量、非线性、强耦合、高阶次、参数不确定性等动力学特性,是自动控制领域研究的重要对象[1-3]。目前，双轮机器人的控制方法仍以传统控制理论居多,最常见的方法是将建模得到的非线性系统做线性化处理,通过比例-积分-微分(简称为PID)控制器或者状态反馈控制器来实现控制[4-5]。由于机器人存在着固有的静态不稳定问题,Keo等[6]提出了利用控制陀螺力矩来实现机器人的倾角稳定;Lam等[7]在此基础上通过比例微分控制器实现了倾角稳定,具有较好的鲁棒性和效率。He等[8]采用极点配置法设计状态反馈控制器实现控制系统的稳定,但极点位置和数目的设计对经验的依赖较大。Hsieh等[9]采用模糊滑模控制器和陀螺平衡器,具有系统响应快、抗干扰能力强等优点。Jian等[10]提出了一种基于粒子群算法的自平衡控制方法,根据线性二次型调节器(linear quadratic regulator, LQR)控制方法对LQR控制器的参数矩阵进行优化,速度快,超调量小。然而,上述传统算法均受到系统模型的制约,对于非线性、时变的、多变量复杂系统往往难以满足控制要求,且多依赖于经验。

强化学习[11-12]是一种不需要先验知识,与环境直接进行交互试错,通过反复迭代得到的反馈信息来获取最优策略的人工智能算法,因而被广泛应用于控制领域中[13-14]。强化学习根据求解方法不同可以分为策略迭代法和值函数迭代法。其中,策略迭代法[15]从一个初始化策略出发,通过策略评估,迭代改进直至收敛来得到最优策略。但在离散空间问题上不能很好地评估单个策略,容易陷于局部最小值,且该方法得到的随机性策略在实际应用中的可靠性难以保证。而值函数迭代法则是根据状态选择动作,得到相应策略。其中,Q-learning算法[16-17]是一种典型的与模型无关的强化学习算法,其状态收敛与初值无关,无需知道模型就可以保证收敛。在状态空间不大的情况下能够很好地构建Q值表,得到最优控制策略。

传统的Q-learning算法主要针对离散状态和离散动作,但实际问题中存在很多连续变量,因此处理连续的动作和状态成为了此类强化学习研究的关键。文献[18]提出了一种线性拟合方法,结合插值函数实现了连续动作输出。本文在以上研究的基础上,针对传统Q-learning在机器人控制方面的不足,引入模糊算法,提出了一种基于模糊强化学习(简称为Fuzzy-Q)算法的双轮机器人侧倾控制方法,实现较大倾角下(0.15°)机器人的姿态控制,使机器人能够抑制跌倒且快速恢复平衡状态。本文的主要研究内容如下:①建立单轨双轮机器人的非线性动力学模型,确定系统的状态转移方程;②针对传统Q-learning算法的不足,引入模糊推理方法泛化系统动作空间,建立输出连续的Fuzzy-Q算法;③基于双轮机器人特性,设计算法的状态空间和动作空间,并结合机器人倾角动态变化设计回报函数,提高训练效率;④通过仿真实验,对比分析传统Q-learning和Fuzzy-Q的学习能力和控制精度,验证所设计算法的有效性和鲁棒性。

1 基于控制力矩陀螺的双轮机器人动力学模型

1.1 控制力矩陀螺

控制力矩陀螺(control moment gyro, CMG)广泛应用于航天器、船舶、自动潜航器等装置的姿态调整[19-20],也在机器人、单轨列车等领域有相关的学术性研究[21]。本文的CMG安装右侧视图如图1所示。其中，O-XYZ是惯性坐标系,车体围绕Y轴旋转,是一个近似的倒立摆,车身倾角为θ。Ob-xbybzb是固连在车体上的坐标系。陀螺框架在CMG进动轴力矩τp的作用下围绕xb轴进动,进动角为γ。Og-xgygzg是固连在陀螺框架上的坐标系。陀螺飞轮围绕zg轴自转,角速度为Ω。其核心是一个高速旋转的飞轮,飞轮安装在陀螺框架上,框架绕与自转轴垂直方向进动时,飞轮的角动量方向会随之发生改变,由于系统满足角动量守恒定律,系统会产生一个与自转轴和框架转轴方向正交的反作用力矩。

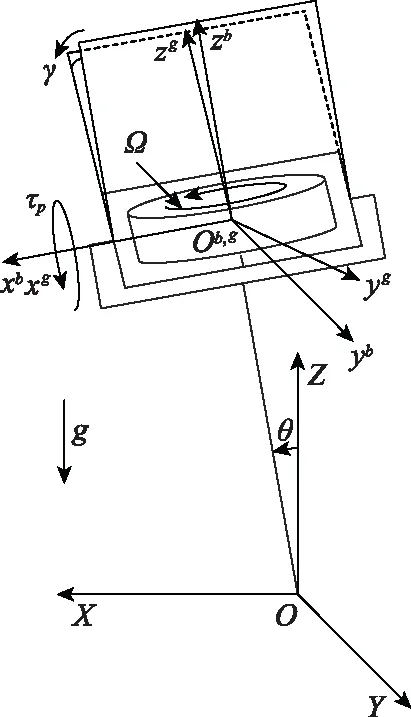
图1 CMG右侧视图

1.2 系统组成及平衡原理

如图2所示,本文设计的CMG机器人系统主要由两个对称安装的CMG和平衡车架组成。

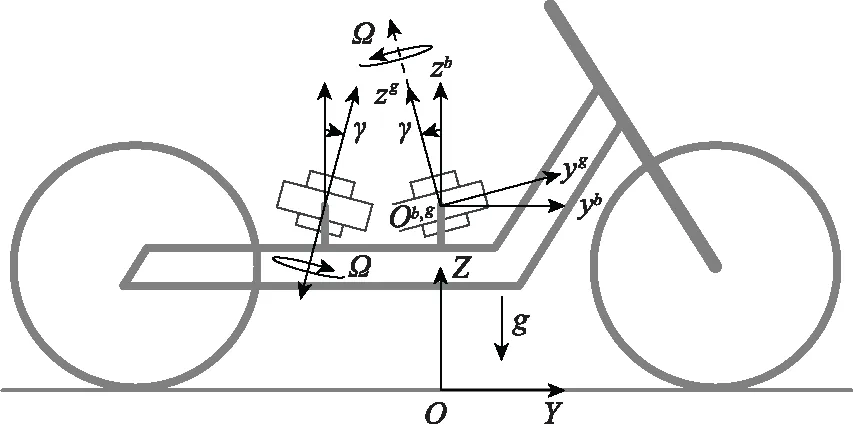
图2 基于CMG的机器人模型

两个CMG自转速度大小相等、方向相反,静止稳定控制时,进动角速度大小相等,方向相反。分析可知,当机器人产生一定的倾斜角时,进动电机施加扭矩使飞轮转子在自转的同时相对车体进动。根据陀螺力矩效应,陀螺进动过程中受到沿进动轴方向外力矩的同时会对车体产生一个反作用力矩τp来抵消重力矩分量以及外界干扰力矩。反作用力矩可表示为

(1)

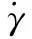
1.3 系统动力学模型

双轮机器人处于运动状态时,其运动速度与车身倾角和车把转向角之间存在着非线性的耦合关系[22-24]。而在静止状态,双轮机器人存在固有的静态不稳定问题,需借助配重或车把来保持平衡。因此,本文通过CMG的方式来实现机器人的姿态平衡控制。

在使用拉格朗日法建立系统的动力学模型和控制模型前,先对系统作如下假设[25-26]:

假设1双轮机器人处于静止状态,即Y向速度为0;

假设2陀螺框架、飞轮都是刚体,车身不考虑车把转向,也是刚体;

假设3轮胎与地面为点接触,不考虑轮胎形变;

假设4不考虑进动方向的摩擦。

同时,选取车身倾角θ,陀螺进动角γ为广义坐标,系统动能为

(2)

式中,mg、mb、mf分别表示陀螺框架质量、车身质量和飞轮质量;Igx、Igy、Igz分别表示陀螺框架主轴惯量;Ifx、Ify、Ifz分别表示飞轮主轴惯量;hb、hf、hg分别表示车身质心高度、飞轮质心高度和陀螺框架质心高度;Iby表示车身主轴惯量。

系统势能可表示为

V=(2mghg+2mfhf+mbhb)gcosθ

(3)

根据拉格朗日方程:

(4)

得到系统的动力学模型:

(2mfhf+2mghg+mbhb)gsinθ-

(5)

(6)

式中,τp作为系统的控制输入,用来保持系统平衡。对于本文的单轨双轮机器人,强化学习的目标是通过大量的学习训练使机器人能在具有初始倾角的情况下根据经验策略实现自主的静止稳定控制。

2 强化学习与Fuzzy-Q算法

2.1 Q-learning算法原理

Q-learning算法是Watkings在1989年提出的一种与模型无关的离线学习算法[27]。Q-learning算法在建立Q值表的基础上,通过机器和环境的交互,得到对应的回报值,再通过不断改进Q值表,使得回报值越来越高[28-29],随之机器人的动作也趋于最优。Q-learning算法的基本形式为

Q(st,at)=α[rt+βmaxQ(st+1,at+1)]+

(1-α)Q(st,at)

(7)

式中,α和β分别表示学习率和折扣因子;α越大则学习速率越快,但受到干扰后的影响越大,可能导致算法不收敛;β表示未来奖励对决策的影响程度,β越大系统更关注长时间内的决策,β越小则更关注最近的决策的影响;st为t时刻机器人的状态,控制器在机器人st状态下输出at,使其状态更新为st+1,并得到奖赏回报rt,表示机器人从st状态到st+1状态获得的回报值;动作at∈A,A为动作空间;状态st∈S,S为状态空间。maxQ(st+1,at+1)表示控制器从动作空间中选择一个动作at+1使得Q(st+1,at+1)的取值最大[30]。Q-learning通过式(7)进行更新,经过N次训练迭代,可得

Q(st,at)=[1-(1-αn)](rt+βQ(st+1,at+1))+

(1-α)Q(st,at)

(8)

由于0<α<1,故当n→∞时,Q(st,at)将收敛于最优值rt+βQ(st+1,at+1)。Q-learning算法本质上属于一种时间差分(temporal difference, TD)算法。与一般TD算法不同,Q-learning的策略核心是状态-动作值函数Q(s,a),即Q-learning将每个状态与动作视为一个整体考虑其性能,并对状态-动作值函数Q(s,a)进行增量式更新,针对Q值表中的值函数Q(s,a),动作选择通常采用ε贪心算法,策略表示为

(9)

即Q值表中最大的Q值对应的动作被选择的概率最大,其他动作被选择的概率相同,以便尽可能地利用已知信息,并保证所有的状态空间都有被探索的机会[31-32]。

Q-learning的算法流程的最终目标就是通过迭代、更新,使得Q值函数收敛[33]。使用Q-learning算法实现机器人的控制,可以直接分析每个状态-动作对,在每个状态下对所能采取的动作进行评价,且Q-learning算法通过离散化的Q值表形式进行了简化,适合作为实现机器人控制的强化学习方法探索。

2.2 Fuzzy-Q算法设计及优化

在初步仿真中发现传统的Q-learning算法由于动作空间离散化,控制器的输出存在高频振荡。实际执行机构难以输出如此剧烈变化的量,且容易对CMG造成损害,同时机器人恢复平衡后的控制精度也有待提高。因此,本文考虑将模糊控制算法与Q-learning算法相结合,即当控制器接收到当前机器人的状态向量之后,通过模糊推理选择一种更合适的动作执行,使执行机构的输出量更加平滑。考虑到模糊控制器的特点,选择以机器人倾角和倾角角速度作为模糊优化的输入量,模糊推理的输出量为控制力矩。

(10)

式中,x为状态空间变量;a、b为待定系数,根据论域范围和模糊空间划分来确定。综合考虑控制性能和模型特点,模糊空间分割采取不等间距划分。在横向比较多种隶属度函数后,本文选用效果最佳的三角形隶属度函数进行模糊化,如图3所示。

图3 倾角隶属度函数

对于系统输出的连续状态,在划分状态区间时,通过隶属度函数将区间模糊化并计算其隶属度,此时每个状态都以相应的隶属度划分到两个子状态中。如T时刻机器人倾角为0.25 rad,则对应以70%隶属于第一状态,以30%隶属于第二状态,倾角角速度的状态区间划分同理,则此时共有4种机器人状态。这4种状态均为强化学习的状态,且每个状态的隶属度为对应两项的隶属度乘积。在每次迭代时,选择4种状态中对应最大的Q值进行学习更新,并通过面积重心法对各个状态的输出进行反模糊化，即

(11)

式中,μk为状态xk对应的隶属度函数;v0为各状态的反模糊化输出值。在更新Q值时,选择对隶属度大于30%的状态进行更新,系统通过反模糊化后得到最终的控制器输出。由于结合模糊理论后算法涉及的状态空间更广,运算量更大,因此需要较长的训练时间才能达到收敛,但学习效果和控制性能比传统的强化学习更优,且抗干扰能力更好。

3 基于强化学习的控制器设计

3.1 状态空间设计

表1 倾角离散区间划分

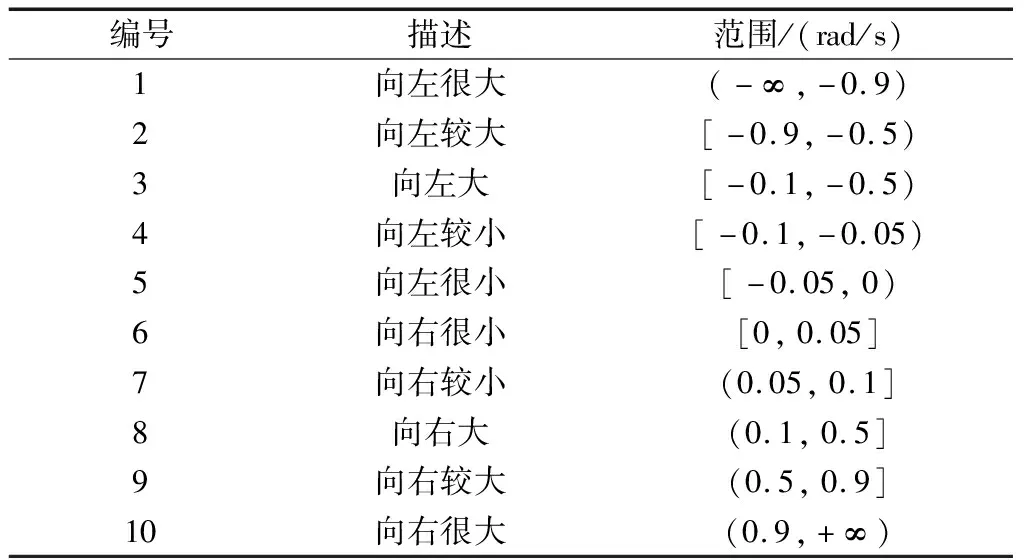
表2 倾角角速度离散区间划分

这样状态空间中的每个元素都对应以上10×10个状态,因此也就生成了100个强化学习状态。

3.2 动作空间设计

在整个控制过程中,机器人的倾角变化由控制器输出的陀螺力矩决定,为避免动作搜索空间过大,对控制器的输出动作进行离散化。根据控制经验,具体的划分如表3所示。

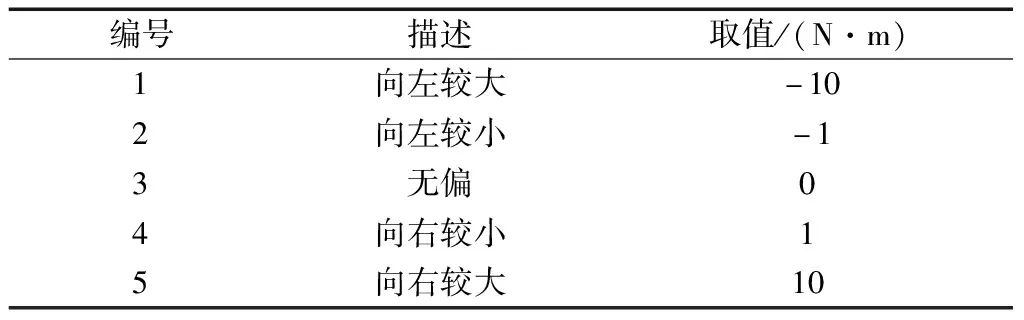
表3 动作离散区间划分

3.3 回报函数设计

强化学习通过状态转移产生的回报函数来对选择的动作进行评估,从而调整Q值表。即回报函数直接决定了Q-learning算法的控制效果和收敛效果,双轮机器人控制的最终目的是使车身倾角θ趋于0,由此设计Q-learning算法回报函数为

(12)

式中,α1和α2表示回报系数,其大小主要由回报评价项的重要性和相对值来决定。为优化回报函数,本文同时将机器人倾角和倾角角速度作为评价量,车身倾角越大,回报惩罚越大,平方项用来加快收敛速度。使得机器人倾角较大时,以角度为回报函数的主要评价项;当倾角较小时(|φ|<5 rad),以倾角角速度为主要评价项,保证机器人在倾角接近0 rad的时候减速,尽量保持在平衡点附近摆动。

3.4 算法流程设计

Q-learning算法采用离散化的Q值表进行值函数的迭代,通过将系统状态和动作人为分割为若干离散序列,从而把连续问题转化为离散的表格化问题。算法的最终目标是使得Q值表中的Q(si,ai)收敛于Q*(si,ai),智能体可根据Q值表做出正确的动作。系统的结构框图如图4所示。

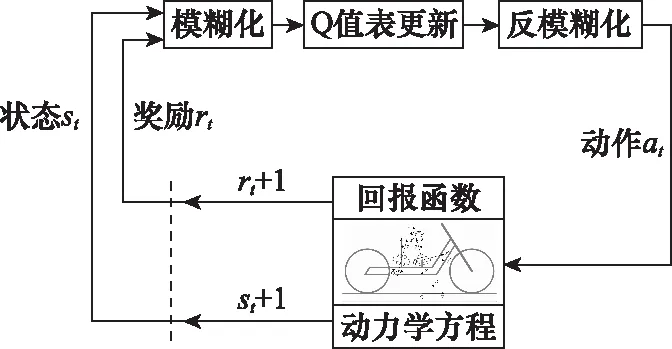
图4 系统结构框图

基于强化学习的单轨双轮机器人控制算法流程图如图5所示。

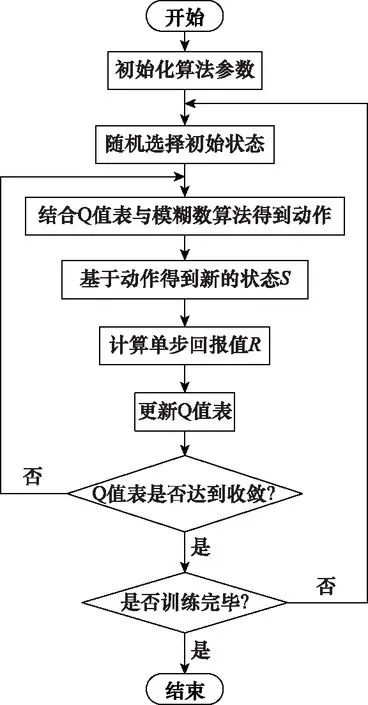
图5 算法流程图

4 仿真结果

本文的算法基于Matlab R2018a环境,训练在英伟达 GeForce GTX 1080 GPU上完成,在训练开始时,任意状态-动作对的Q值初始化为0,且机器人的初始倾角10 rad,CMG的进动轴力矩大小由强化学习算法得到的动作输出获得,当机器人倾角大于30 rad,则整个环境进行复位,重新学习,直到倾角能够保持在0 rad左右并维持一段时间。整个训练过程中,系统模型参数基于机器人实物如图6所示,涉及的具体参数和数值如表4所示。

图6 机器人实物图

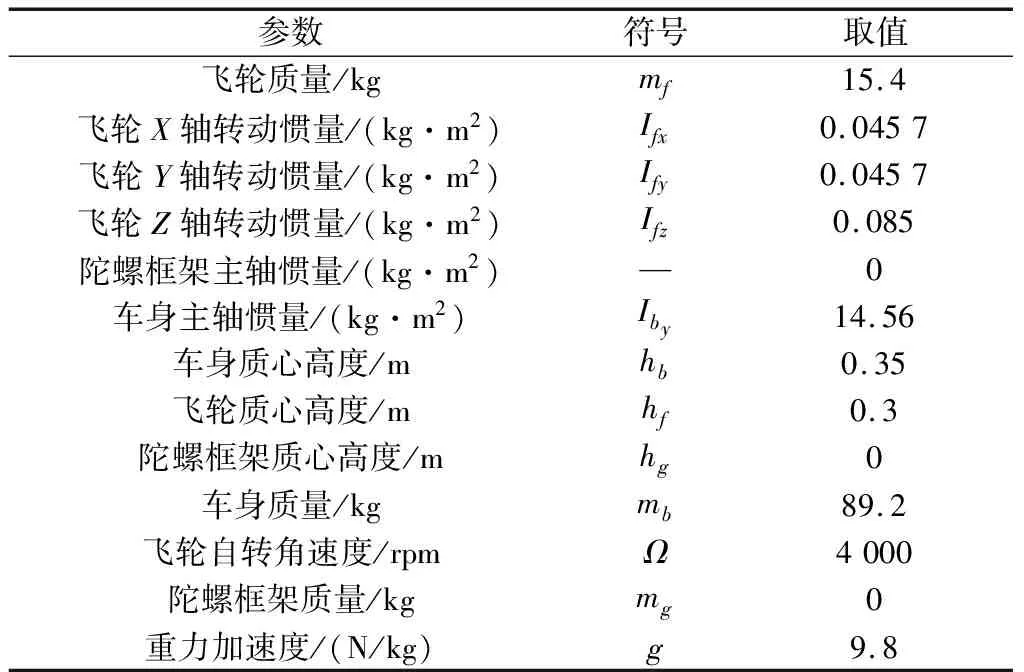
表4 机器人模型参数

4.1 Q-learning算法下的姿态稳定控制

采用Q-learning算法实现机器人控制,在经过约5分钟的反复训练后,仿真结果如图7所示。

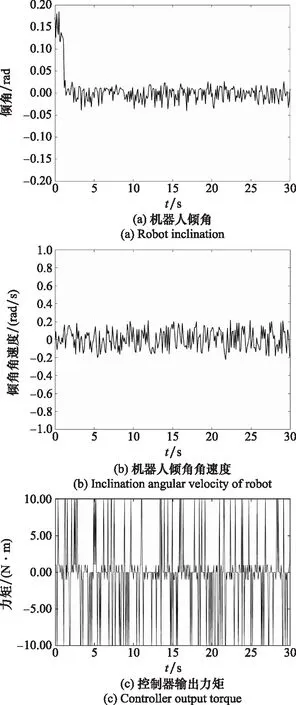
图7 Q-learning算法下机器人控制仿真结果

可以看到训练成功后,机器人的倾角在3 s左右就可以趋于收敛,控制精度为0.025 rad,同时倾角角速度的变化范围为±0.2 rad/s,这主要是通过动作空间中的大幅度动作(±10N)配合小幅度调整动作(±1 N)以及静止动作(0 N)来实现的。说明在模型未知且无任何先验知识的条件下,控制器通过强化学习可以很快的控制平衡,且控制精度较高。

图8为训练过程中的回报函数值。可以看出,在训练初期,由于动作的选择处于探索阶段,具有一定的随机性,因此获得的回报值较小。但在经历了1 000次左右的学习之后,Q值表逐渐得到完善,智能体获得的奖励也越来越高,算法最终达到收敛。

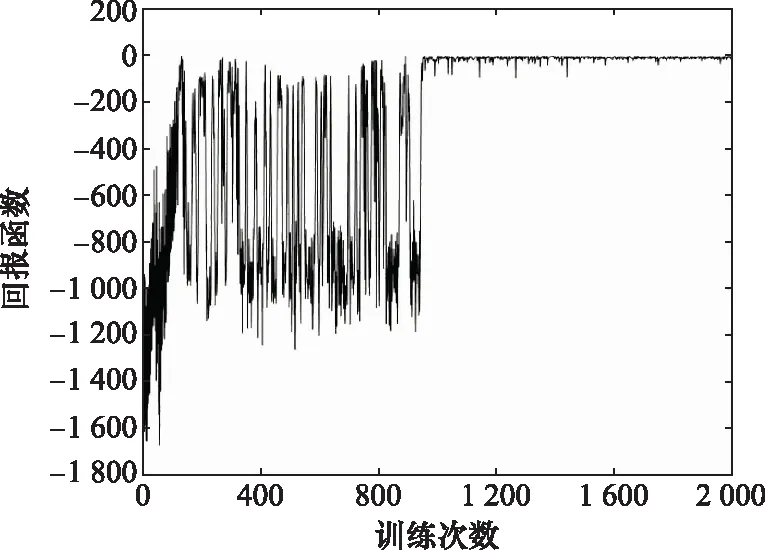
图8 Q-learning算法的回报函数

4.2 Fuzzy-Q算法下的姿态稳定控制

从仿真结果可以看到,由于Q-learning算法的离散化,控制器输出振荡幅度较大。为改善控制器输出并提高控制精度,本文在强化学习的基础上改进并设计了Fuzzy-Q算法,其仿真结果如图9所示。

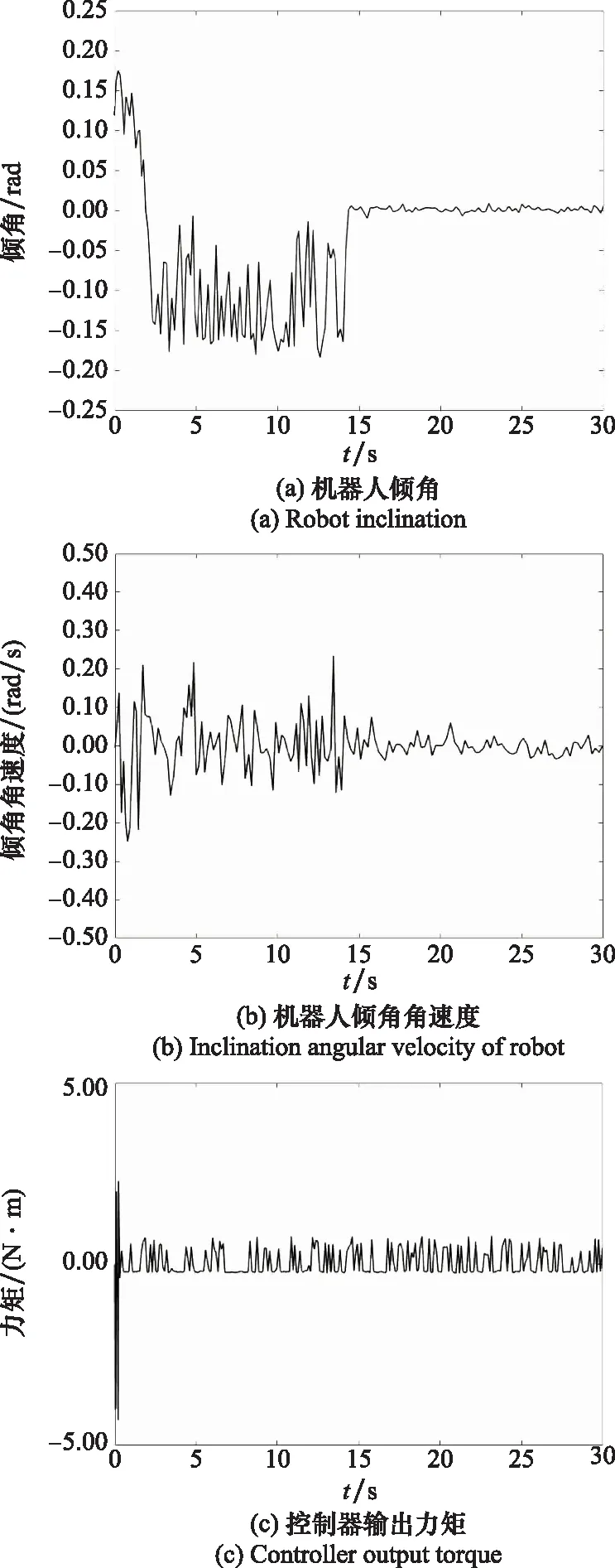
图9 Fuzzy-Q算法下机器人控制仿真结果

图9(c)是采用了Fuzzy-Q算法的控制器输出,可以看到,在训练成功后的控制周期内,陀螺力矩的输出值较为平滑,未发生剧烈的突变,整个控制过程较为平顺。

同时,在采用了Fuzzy-Q算法之后,机器人的控制精度为±0.01 rad,且倾角角速度收敛于±0.2 rad/s。由此可以证明整个训练过程是成功的,机器人在此时已经学习到了一个最优策略,达到了较高的控制精度。同时,控制器的输出为连续信号,比传统强化学习的控制效果更好。证明了在传统强化学习的基础上引入模糊算法,可以将离散控制器转化为连续控制器,控制效果上可以得到明显改善。

图10为训练过程中的回报函数值变化曲线。可以看到,累积回报值在训练开始时并不稳定,随着训练周期及次数增加,总体变化趋势逐渐增大,即随着训练次数的增加最终趋于稳定值。证明算法实现收敛,且训练次数比Q-learning算法更短,学习能力更强。

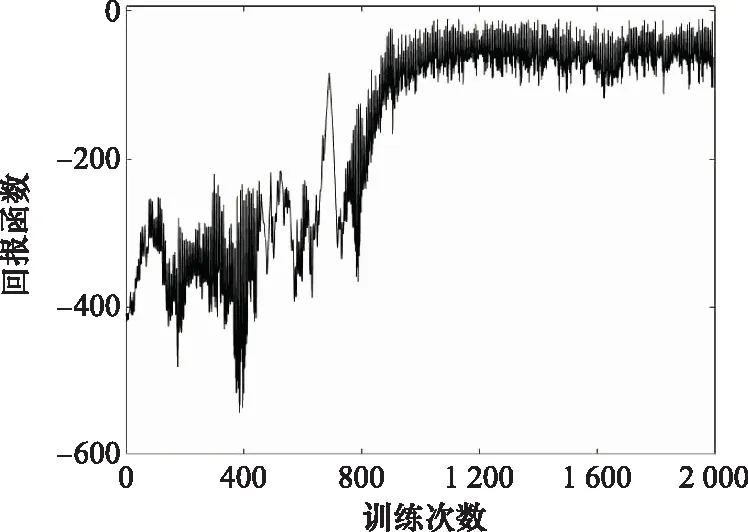
图10 Fuzzy-Q算法的回报函数

4.3 外加力矩干扰下的姿态稳定控制

为分析系统的抗干扰能力,在训练成功后,人为地加入扰动,具体做法为在21 s时对处于平衡状态的机器人施加脉冲干扰力矩(9 N·m),倾角受到扰动后恢复情形的仿真结果如图11所示。

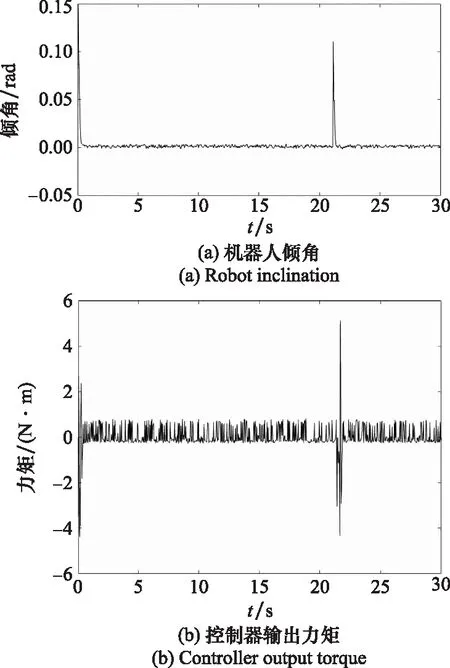
图11 受干扰时机器人控制仿真结果

可以很明显地看到,在加入干扰之后,车身倾角出现了轻微增加,偏离角度约为0.116 rad,同时控制器迅速做出反应调整输出,最终使机器人倾角平稳地恢复到了平衡位置,整个过程花费时间约为1 s,证明了Fuzzy-Q算法具有较强的鲁棒性,在受到干扰后倾角偏离角度较小且恢复时间短。

5 结 论

本文设计了一种基于CMG和Q-learning算法的机器人侧倾姿态稳定控制方法,实现了[-0.01,0.01]rad控制精度内的机器人静止平衡控制。在传统强化学习的基础上,结合模糊理论建立了Fuzzy-Q算法,以模糊输出代替Q值函数输出,解决了Q-learning算法存在的控制器输出高频振荡的问题,避免了在实际应用中对执行机构造成损伤。同时基于机器人特性优化回报函数,提高了学习效率。结果表明,经过训练后,本文所设计的Fuzzy-Q算法能够快速平稳地实现机器人的侧倾稳定控制。相较于传统的强化学习方法,Fuzzy-Q算法学习时间更短,控制精度更高且具有较强的抗干扰能力,能够实现单轨双轮机器人侧倾稳定的控制目标。