考虑SAR量测特性的弹载SINS/SAR组合导航滤波算法

苏 敬, 何华锋, 何耀民, 王依繁, 韩晓斐

(火箭军工程大学导弹工程学院, 陕西 西安 710025)

0 引 言

捷联惯性导航系统(strapdown inertial navigation system,SINS)能够不依赖外部信息自主导航,但其导航误差会随时间而积累[1]。合成孔径雷达(synthetic aperture radar,SAR)是一种全天时的主动观测系统,广泛应用于军事领域[2]。复合末制导过程中弹载SAR能够提供弹体精确的位置和航向信息,实现对SINS导航误差的修正,提高导航精度。

组合导航系统的滤波方法多为常规卡尔曼滤波(Kalman filter,KF)或其改进方法[3-6],通常仅对线性系统具有较好的适应性,而真实条件下跟踪系统的状态模型和量测模型必然是非线性的。因此,有学者提出利用无迹KF[7](unscented KF, UKF)作为惯导/天文组合导航系统的滤波方法,仿真结果证明在相同观测方案下,非线性滤波方法定位性能更高。SINS/SAR组合导航系统在导航定位时,SINS的输出周期通常为10～50 ms,SAR成像与基准图匹配运算通常有1～5 s的随机延时,产生系统量测非等间隔输出和量测信息滞后两个问题,导致无法及时修正惯性导航误差,影响滤波精度。

针对非等间隔量测的问题,文献[8]在惯性导航系统(inertial navigation system, INS)/SAR组合导航系统中利用INS的信息增量修正SAR非等间隔量测造成的误差,但实际上SAR量测输出的时间间隔是随机的,且与INS采样率相差较大,因此该方法可行性不高。文献[9]在KF算法基础上,根据有无量测信息输出,分别采取多模型方法或插值方法获得量测预测,进而修正系统状态。文献[10]提出采用多尺度分块融合算法,分别将状态信息和观测信息在不同尺度上进行KF,进而解决不同传感器非等间隔量测的问题。但是文献[9-10]均是实现于KF算法基础之上,不适用于非线性系统。针对量测滞后问题,文献[11]结合SINS/SAR组合导航系统特点,利用SAR等效量测量和追溯状态向量来估计当前状态,进而修正INS误差,但由于简化了量测矩阵为单位阵,其追溯状态向量有一定误差,因此对导航精度的提升有限。文献[12]在解决INS/SAR非等间隔量测问题基础上,提出利用INS信息增量递推当前时刻SAR量测,实现组合滤波,虽然INS短期精度较高,但是弹载SAR的图像匹配和定位时间间隔较长,将会影响INS量测精度,降低算法的稳定性。另外，量测滞后问题本质是无序测量[13-14]问题,常用的滤波方法包括重新滤波法[15]、数据缓存法[16]、曲线拟合法[17]等,前两种方法滤波精度最高,但是计算量较大,曲线拟合法可根据导弹飞行动态和精度要求,选取不同的曲线拟合导航系统量测值,方法灵活且滤波精度较高。

本文采用非等间隔UKF算法和抛物线拟合补偿法得到了一种适用于弹载SINS/SAR组合导航系统的滤波算法。根据SAR有无量测输出选择是否进行量测更新,进而解决了量测不同步的问题。然后，利用抛物线拟合补偿法拟合SAR输出信息,获得SAR量测信息滞后的补偿算法。仿真结果证明本文提出的算法能够有效提升组合导航系统滤波精度。

1 弹载SINS/SAR组合导航系统数学模型

由于SAR只能提供导弹水平的位置信息和航向信息,不能提供导弹的高度信息,因此需加入气压高度计的输出作为系统观测量,以抑制组合系统高度通道的发散。

1.1 组合系统的状态方程

将东北天地理坐标系选为导航坐标系,结合SINS误差源分析[18],建立SINS/SAR组合导航系统状态方程：

(1)

式中,系统状态变量为

X=[δθ，δV，δP，ε，Δ]T

(2)

式中,δ为各变量误差；δθ=[θx，θy，θz]T为姿态角误差;δV=[δvx，δvy，δvz]T为速度误差;δP=[δL，δλ，δh]T为位置误差;ε=[εx，εy，εz]T为陀螺常值漂移误差;Δ=[Δx，Δy，Δz]T为加速度计零偏；F(t)，G(t)和W(t)分别为状态转移矩阵、噪声系数矩阵和系统噪声[8]。

1.2 组合系统的量测方程

在组合系统中,水平方向量测由SINS和SAR输出的航向角度之差、经度之差和纬度之差构成;高度方向量测由SINS和气压高度计输出的高度之差构成。量测方程为

Z(t)=H(t)X(t)+V

(3)

式中,H(t)和V分别是量测矩阵和量测噪声。Z(t)具体形式为

(4)

式中，θI，LI，λI，hI分别为SINS测得的航向角和位置误差信息；θS，LS，λS为SAR测得的航向角和水平位置信息；he为气压高度计的输出值；δθu，δL，δλ为SINS与SAR的量测差值；δh为SINS与高度计的量测差值；v1，v2，v3分别为SAR图像匹配输出时的航向角误差、东向位置误差以及北向位置误差；v4为气压高度计输出时的高度误差；RM和RN为参考椭球子午圈和卯酉圈上各点的曲率半径[8]。综合式(3)和式(4)，量测矩阵可表示为

H(t)=

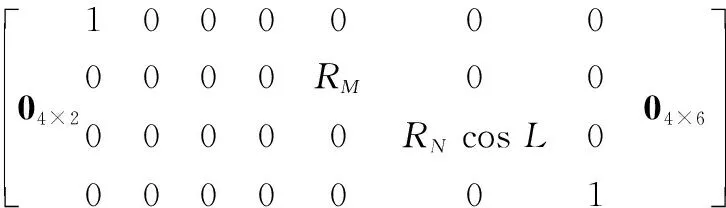
(5)

2 考虑非等间隔量测的非线性滤波算法

2.1 UKF算法原理

UKF核心思想是利用若干近似高斯分布的样本点[19],通过无损变换(unscented transformation,UT)获得测量条件下误差和协方差的递推及更新,实现对目标的跟踪。

2.1.1 UT变换

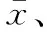
(6)

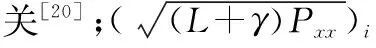
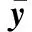
(7)

2.1.2 UKF算法步骤

结合第1.1节和第1.2节,将SINS/SAR状态方程和量测方程离散化得

(8)

式中,k为离散化后的采样时刻；uk为输入向量;ωk和vk为高斯白噪声;方差阵分别为Qk，Rk。设xk，ωk，vk维数分别为n，p，q,考虑噪声项，对状态进行扩维得xa=[xT，vT，ωT]T,状态的初始条件即为

(9)

步骤 1Sigma点采样

采用对称采样策略[22],得到采样点公式如下:

(10)

式中,L=n+p+q。

步骤 2时间更新

(11)

步骤 3量测更新

(12)

由上述步骤可得到对称采样下的UKF算法。

2.2 非等间隔UKF设计

2.2.1 SAR非等间隔量测输出特点

设SINS和SAR的导航周期分别为TSINS和TSARi(i=1,2,…),状态方程离散化周期为T,令T=N×TSINS,TSARi=Mi×T,为方便计算,设Mi和N均为正整数。可得SINS导航周期、系统离散化周期与SAR量测输出时间间隔关系如图1所示。

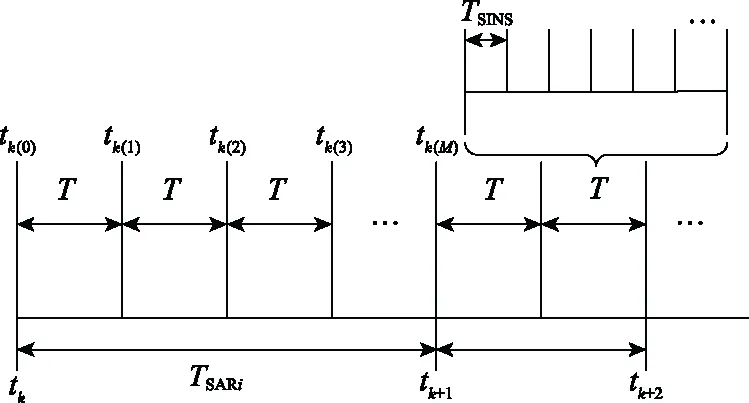
图1 非等间隔量测的时间关系

图1中,tk,tk+1,tk+2为SAR输出时刻,且各个时刻的输出间隔不等。

2.2.2 基于SINS/SAR组合导航的非等间隔UKF算法

由第2.1.2节可知,常规UKF算法分为时间更新和量测更新,同时结合SAR量测非等间隔输出特点,利用状态转移矩阵的特性设计非等间隔UKF算法。将SINS/SAR组合导航滤波分为两步[23],即在SAR没有量测输出的时刻tk(j)(j=0,1,…,M-1)仅进行UKF时间更新;在SAR有量测输出的时刻tk(M)同时进行UKF时间更新和量测更新。

在tk(j)(j=0,1,…,M-1)时刻的时间更新:

(13)

在tk(M)时刻时间更新和量测更新:

(14)

(15)

3 解决SAR量测滞后的曲线拟合补偿法

由于SAR图像匹配输出具有滞后性。设在tk时刻提出匹配申请,无法获得该时刻的实时量测,只能得到tk-1时刻的量测信息,如图2所示。若用滞后的量测量修正SINS状态量,必然会降低组合导航精度,因此需对滞后的量测量进行补偿。

图2 SAR图像匹配量测滞后时序图

本文采用抛物线曲线拟合法,在[tk-3,tk]时间内,对量测值Zk进行拟合:

Z(t)=a(t-tk-3)2+b(t-tk-3)+c

(16)

则有

Zk-3=c

(17)

Zk-2=a(tk-2-tk-3)2+b(tk-2-tk-3)+c

(18)

Zk-1=a(tk-1-tk-3)2+b(tk-1-tk-3)+c

(19)

联立式(16)～式(18)求得

(20)

将式(20)代入式(16)即可得k时刻SAR量测输出：

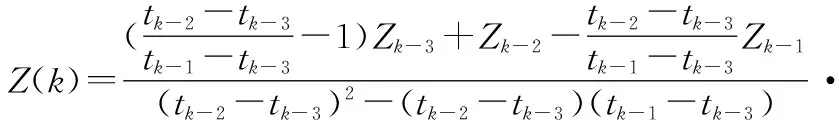
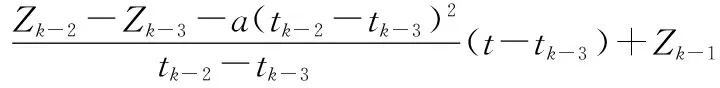
(21)

针对弹道导弹再入段工作特点还可选择3次抛物线拟合[24],拟合精度会进一步提高,但同时也会增大计算量。

4 弹载SINS/SAR组合导航系统仿真及分析

4.1 初始条件设置

导弹进入再入段后SAR导引头开机,依次完成测高、成像、匹配、定位,实现SINS/SAR组合导航。设SINS输出周期为0.01 s,状态方程离散化周期为0.1 s,SAR图像处理时间为1～5 s的随机整数。

设平台初始姿态角误差分别为200 ″、200 ″和300″,东北天初始速度误差均为1 m/s,东向和北向初始位置误差为30 m,高度初始误差为50 m。SAR水平位置、方位角定位精度误差分别为30 m和0.5 °,高度表误差为20 m。惯性器件误差如表1所示。

表1 惯性器件误差

4.2 仿真结果及分析

对弹载SINS/SAR组合导航系统进行了70 s末制导仿真，分别采用常规UKF算法(算法1)、考虑SAR非等间隔量测的UKF算法(算法2)和考虑SAR非等间隔量测及量测滞后的UKF算法(算法3)予以仿真分析，并对比了东向位置误差、航向角误差和北向速度误差，结果如图3～图5所示。

图3 弹载SINS/SAR组合导航系统东向位置误差

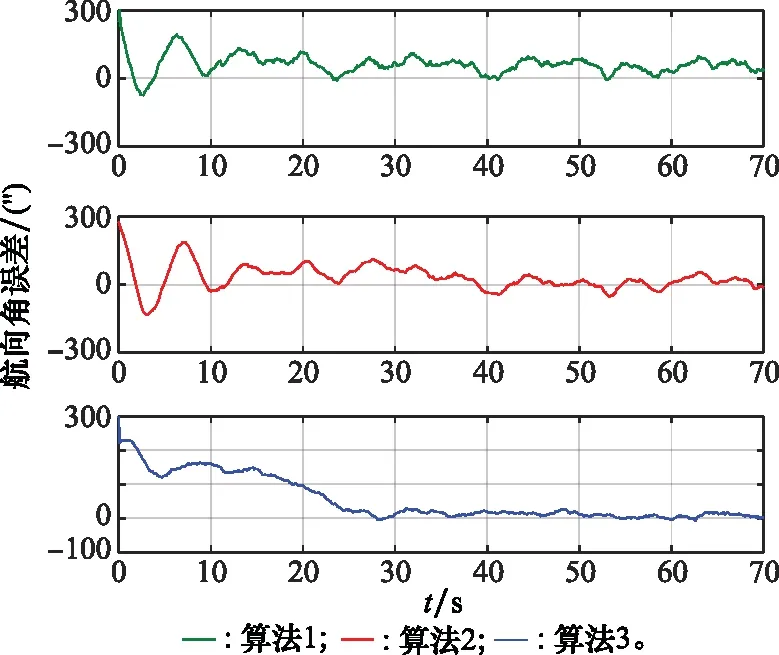
图4 弹载SINS/SAR组合导航系统航向角误差

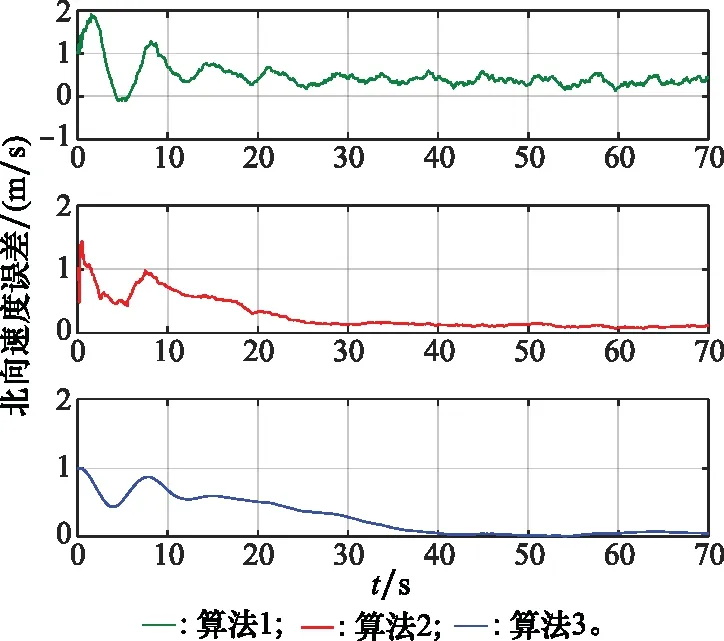
图5 弹载SINS/SAR组合导航系统北向速度误差

仿真结果表明,在弹载SINS/SAR组合导航系统中,与传统的滤波算法相比,考虑SAR非等间隔量测特性的滤波算法能够提升其滤波精度。而在此基础上采用曲线拟合法对SAR量测滞后进行补偿的滤波算法则能够将东向位置误差绝对值由13.56 m降到5.12 m,将航向角误差绝对值由38.56″降到6.63″,将北向速度误差绝对值由0.59 m/s降到0.08 m/s,显著地提升了组合导航系统的滤波精度。不同滤波算法得到的组合导航系统的滤波精度如表2所示。

表2 弹载SINS/SAR组合导航系统滤波精度

为进一步验证滤波算法的精度,重复10次SINS/SAR组合导航系统末制导仿真,以东向位置误差仿真结果为例,对比分析3种方法的统计结果。根据统计方法得其估计值为

(22)

表3为采用算法①时,东向位置误差仿真结果的绝对值。

表3 东向位置误差仿真结果

当υ=0.1时,由式(22)计算得到估计值为μ=13.26±1.49。由此可以得出,采用算法1时SINS/SAR组合导航系统的东向位置误差以90%的置信度位于区间[11.77,14.75]。同理,采用算法2及算法3时东向位置误差以90%的置信度分别位于[7.36,10.22]及[4.37,5.89]。

由统计分析结果可看出,相同置信度下,本文提出的算法求解组合导航系统东向位置误差的精度要明显高于传统滤波算法,进一步验证了本文所提算法的有效性和可靠性。

5 结 论

为解决弹载SINS/SAR组合导航系统中非等间隔量测及SAR量测信息滞后的问题,本文在分析了常规UKF算法的基础上,提出了一种利用曲线拟合补偿法解决量测滞后的非等间隔UKF算法。仿真结果表明，本文提出的算法能够解决SINS/SAR非等间隔量测的问题,并能够有效补偿量测滞后,验证了该算法相比于常规UKF算法具有更高的滤波精度。同时，本文提出的算法也可用于其他组合导航系统,因此该滤波算法具有一定的工程应用前景。