基于恒比鉴别和小波变换的脉冲激光雷达成像

左靖昊,张彦梅,栾晨辉

(北京理工大学信息与电子学院,北京 100081)

1 引 言

成像激光雷达在民用和国防目标探测与识别领域有着广泛的应用。成像系统的分辨率取决于用于成像的电磁辐射的波长,较短的波长通常会产生较细的细节。由于成像激光雷达的工作波长远小于普通微波雷达,因此它可以生成高分辨率物体图像,从而实现精确的目标识别。成像激光雷达的高分辨率依赖于有效的检测算法来减轻杂波。杂波识别算法是当前研究的热点。

2007年,瑞典Saab Bofors公司与瑞典皇家工学院合作,建立了激光近炸引信三维成像探测仿真系统,用于对激光引信数字探测算法进行性能仿真[1]。研究中重点对数字恒比鉴别算法与匹配滤波算法进行了性能仿真对比,通过对比得出数字匹配滤波算法具有更好性能。2010年,南京理工大学陈钱、徐彤等对激光近炸引信定距算法进行了研究,实现了小波变换定距算法[2]。采用基于TI 公司DM642 型号的DSP芯片硬件电路,对示波器采集激光回波原始数据进行小波变换数字信号处理,算法最小实现周期为0.992 ms,在10 m处定距精度达到了±0.45 m。2016年,北京理工大学李欢、郭海超等提出了一种新的混合脉冲检测算法,该算法结合了匹配滤波算法和恒比鉴别(CFD)算法[3],在减轻杂波方面具有较好的性能,而且有着较高的测量精度。然而,当杂波信号较大时,上述方法的成像性能通常会较差。

为了提升脉冲激光雷达的成像性能,本文基于MATLAB创建了由激光脉冲发射、杂波干扰、激光脉冲接收和生成目标图像构成的仿真模型,提出了一种恒比鉴别算法和小波变换算法相结合的复合算法,与恒比鉴别算法,小波变换算法,匹配滤波算法,恒比鉴别与匹配滤波复合算法相比较,具有更好的成像性能。同时,提出了一种基于新型的阈值函数的小波变换与恒比鉴别算法相结合,在减轻杂波方面具有更好的性能。

2 成像激光雷达仿真模型

成像激光雷达仿真模型由激光脉冲发射、杂波干扰、激光脉冲接收和生成目标图像四部分构成[3]。仿真中使用的激光雷达脉冲发射功率方程[4]如公式(1)所示,P0是峰值功率,T1/2为激光脉冲波形的半功率宽度。

(1)

本文仿真的激光脉冲的半功率宽度为100 ns,峰值功率为220 W,激光雷达发射脉冲时间分布功率图如图1所示。

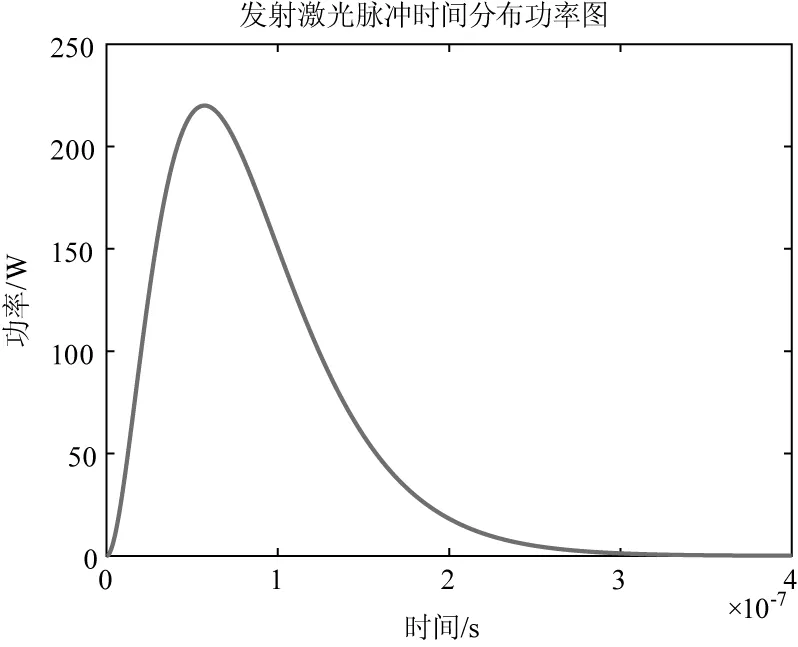
图1 激光雷达发射脉冲时间分布功率图

在不考虑杂波的环境下,激光脉冲回波信号受到距离、大气等因素的影响,激光雷达接收脉冲功率方程[5]可表示为:

(2)

其中,TA为大气的单程透过率;ρ为目标的激光漫反射系数;D为接收光学系统的孔径;ηt和ηr分别是发射光学系统和接收光学系统的透过率;Mt为探测器的增益系数;R为目标到激光测距系统的距离。

激光雷达接收脉冲时间分布如图2所示,从图中可以看出,在不考虑杂波的环境下,受到距离、大气等因素的影响,激光脉冲回波信号的功率大大减小。

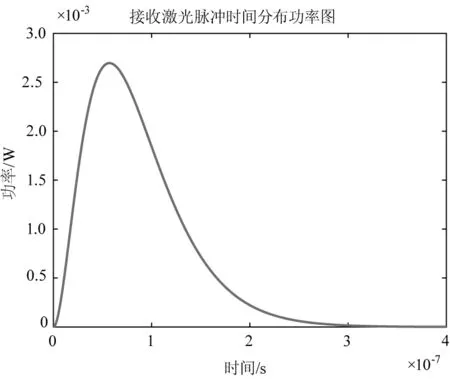
图2 激光雷达接收脉冲时间分布功率图

激光脉冲信号除了会受到大气影响之外,还会受到杂波和噪声的干扰。杂波信号主要是由树木、草丛、建筑物等周围环境反射的回波,常见的杂波有瑞利分布的杂波,对数正态分布杂波、韦布尔分布杂波。

瑞利分布杂波幅度概率密度函数如公式(3),其仿真序列图如图3所示。海杂波地杂波等对低分辨率雷达的杂波幅度服从瑞利分布模型[6]：

(3)

式中,α为瑞利参数,瑞利分布的期望值为:

(4)

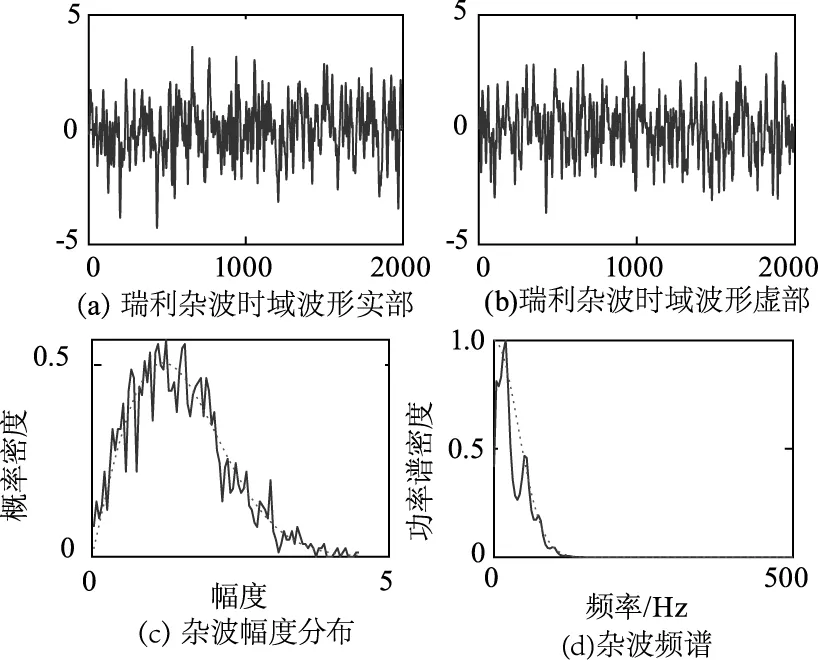
图3 瑞利分布仿真序列图

对数正态分布杂波概率密度函数如式(5)所示,时间波形图如图4所示。对数正态分布适用于低入射角或者海面平静的高分辨率海杂波信号的仿真[7]。

图4 对数正态分布仿真图

(γ>0,σc>0,μm>0)

(5)

式中,μm为尺度参数;γ为中值;σc为形状参数。对数正态分布的期望值为:

(6)

韦布尔分布杂波模型概率密度函数如公式(7)所示：

(x≥0,p>0,q>0)

(7)

式中,p为形状参数;q为尺度参数。韦布尔分布的期望值为:

E(γ)=qΓ(1+p-1)

(8)

式中,Γ(·)为伽马函数。韦布尔分布杂波模型适应于更广泛的环境,通过调整参数,能得到接近瑞利分布杂波模型和对数正态分布杂波模型的杂波分布[8]。时间波形图如图5所示。

图5 韦布尔分布仿真图

由于受到杂波和噪声的影响,激光雷达脉冲接收信号的表达式如式(9)所示:

Preceive=Pr+Pclutter+Pnoise

(9)

其中,Pclutter是杂波的强度信号;Pnoise是噪声的强度信号。噪声一般都是高斯白噪声。

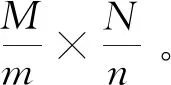
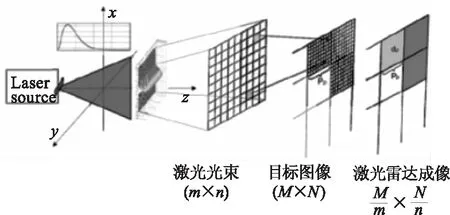
图6 激光雷达成像仿真原理图

3 杂波识别算法模型

3.1 恒比鉴别算法

恒比鉴别算法是将输入信号分成两个通道,将一个通道的输入信号延迟一个脉冲宽度的一半,然后用原始通道中的信号减去延迟通道的信号,得到s形信号。这种信号的过零点对幅度波动非常不敏感。

3.2 小波变换算法

3.2.1 小波分析降噪过程

小波变换是一种特征提取和低通滤波的综合算法,其流程图如图7所示。

图7 小波变换流程图

基于阈值的小波变换算法的原理是,选定一种小波对信号进行N层分解,分解过程如图8所示,cAn,cDn分别反映信号的第n层分解的近似系数与细节系数,近似系数表征了信号的低频部分信息,细节系数则表征了信号的高频部分信息。

对激光雷达脉冲接收信号单层分解产生的近似系数与细节系数如图9所示。从图中可以看出,近似系数主要反映脉冲信号的信息,细节系数主要反映杂波和噪声的信息。携带信息的脉冲信号在小波域的能量比较集中,表现为能量密集区域的信号分解系数的绝对值比较大,噪声和杂波的能量谱比较分散,其系数的绝对值较小,因此可以通过作用阈值的方法过滤掉绝对值小于一定阈值的小波系数,对分解得到的各层系数选择一个阈值,对细节系数软阈值处理。处理后的系数通过小波进行重建得到原始信号。

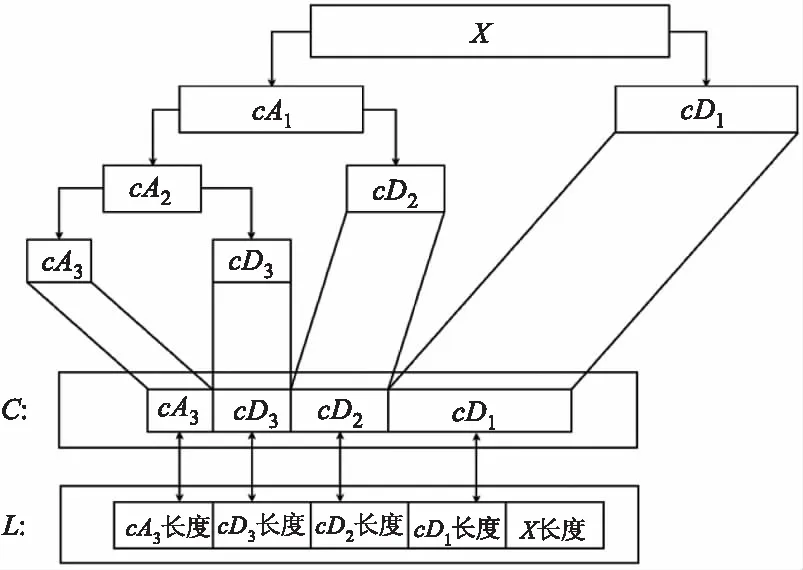
图8 小波变换分解流程图

图9 小波变换的近似分量与细节分量

3.2.2 Birge-Massart阈值法

在小波分析用于降噪的过程中,核心的步骤是在系数上作用阈值,因为阈值的选取直接影响降噪的质量,进而影响图像的质量。阈值的确定主要有以下三个数学模型:由Donoho-Johnstone提出的阈值确定模型,Birge-Massart策略所确定的阈值模型,小波包变换中的penalty阈值模型,除了Birge-Massart策略确定的阈值外,其余方法得到的降噪信号太过于光滑,失去了原信号本身的一些信息,因此本文用Birge-Massart策略确定的阈值:给定一个指定的分解层数j,对(j+1)及更高层所有系数保留,对第i层(1≤i≤j)保留绝对值最大ni个系数,ni由式(10)确定：

ni=M(j+2-i)α

(10)

式中,M和α为经验系数,缺省情况下取M=L(1),也就是第一层分解后系数的长度。一般情况下,M满足L(1)≤M≤L(2),本文α取7。

3.2.3 硬阈值与软阈值

在求得阈值后,有两种在信号上作用阈值的方法,一种是令绝对值小于阈值的信号点的值为零,成为硬阈值,如式(11)所示,这种方法的缺点是在某些点会产生间断。

(11)

式中,W表示小波系数的值;Wt是处理后的小波系数值;λ是阈值。

另一种软阈值方法是在硬阈值的基础上降边界出现不连续点收缩到零,如式(12)所示。这样可以有效避免间断,使重建的信号比较光滑,但是软阈值函数的原系数和小波分解系数存在恒定偏差。

(12)

由软阈值函数可等价如下方程:

(13)

3.2.4 新阈值函数

为了更好地分离有用信号和无用噪声,我们在新提出的阈值函数,对W/λ进行指数化处理,使得每一个系数与1的偏离程度增大。同时,为了同时利用到硬阈值法可以更多保留真实信号中的尖峰特征,以及软阈值法连续性好,重建信号平滑的优点,我们使用在提出的阈值函数中,引入一个折中余量,以更好提取到有用信号。本文提出了一种新的阈值函数,如式(14)所示：

(14)

其中,sign(·)是符号函数;W表示小波系数的值;Wt是处理后的小波系数值;λ是阈值;0≤α≤1,本文α取0.5,n≥1,本文n取3。

图10显示了三种阈值函数的图形示意图,从左到右依次为硬阈值、软阈值和新阈值函数。

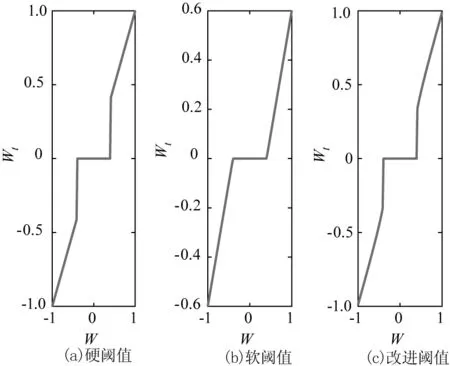
图10 硬阈值、软阈值和新阈值函数的图形

复合检测算法是将小波变换算法和CFD算法相结合的新方法。复合算法的仿真方案如图11所示。基于新型小波变换的复合算法的仿真如图12所示。

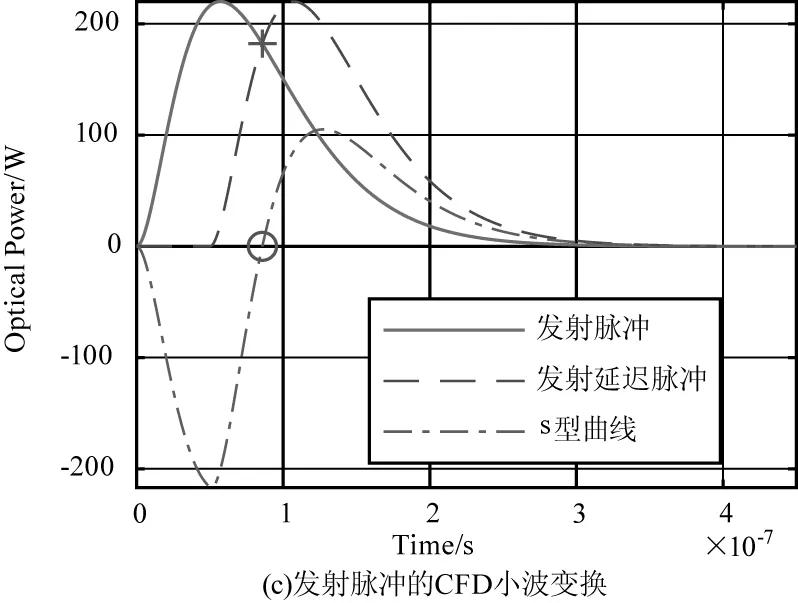
图11 复合算法的仿真方案

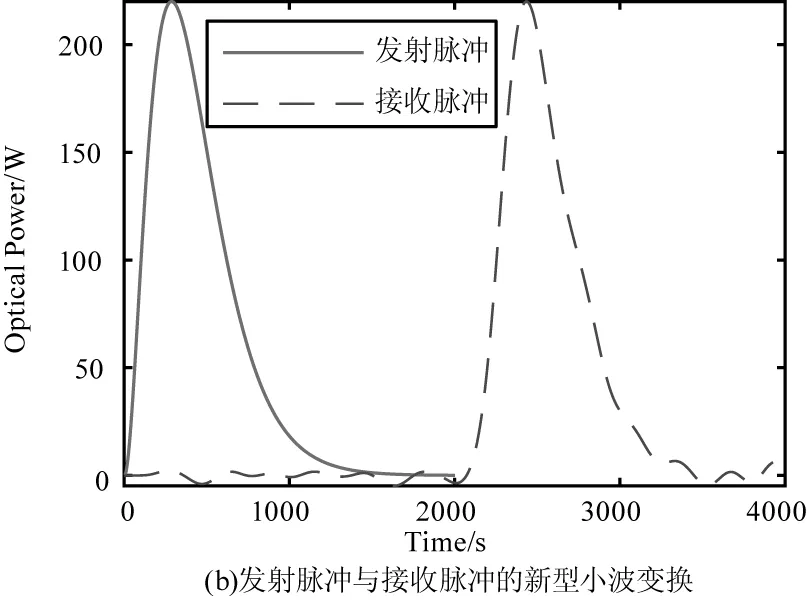
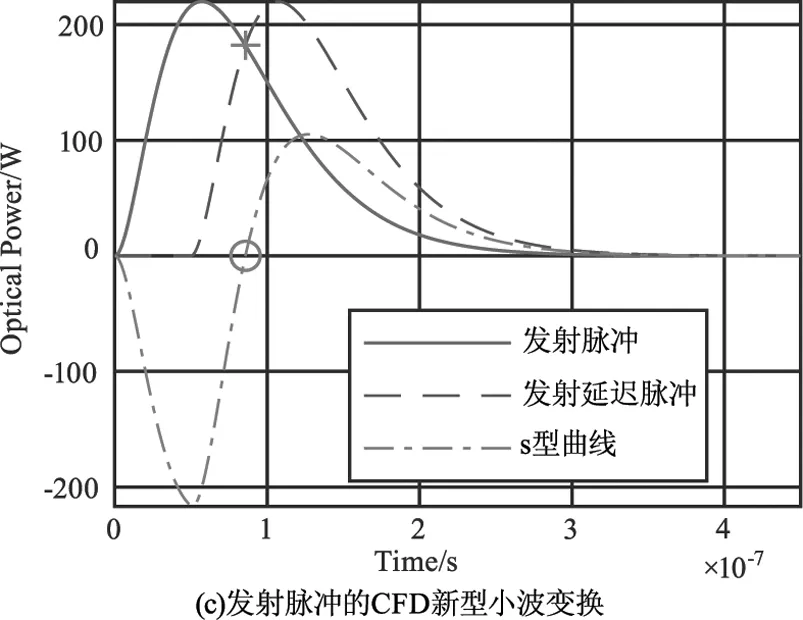
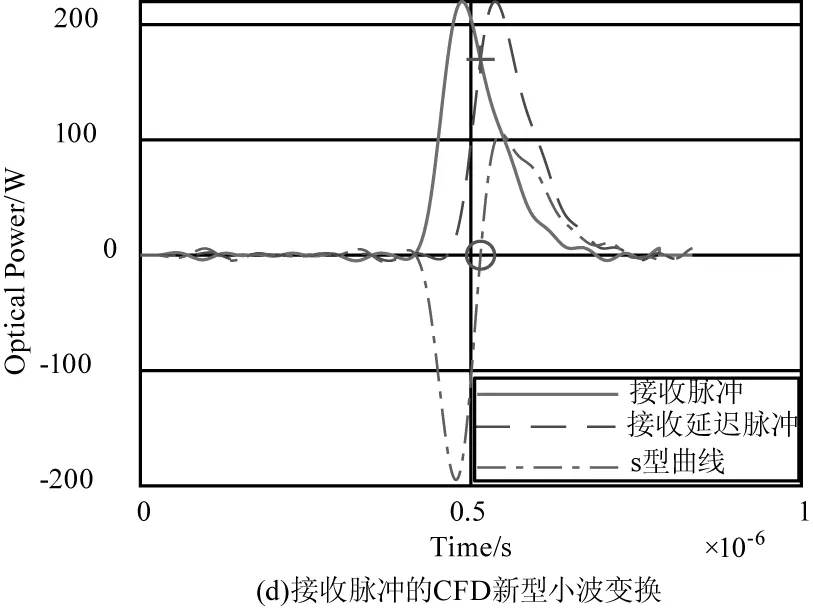
图12 改进复合算法的仿真方案

与发射脉冲相比,接收脉冲是一个非常微弱的信号。因此,为了观看方便,接收脉冲和发送脉冲都被标准化为220 W。图11(a)以实线示出了由激光二极管发射的激光脉冲,并且以虚线示出了由激光检测器接收的激光脉冲。通过小波变换处理发送的脉冲信号和接收的脉冲信号,处理结果如图11(b)和图12(b)所示。接下来使用CFD算法,通过处理图11(b)和图12(b)中的发射脉冲,激光脉冲触发时间如图11(c)和图12(c)所示。通过处理图11(b)和图12(b)中接收到的脉冲,激光脉冲回波接收时间如图11(d)和图12(d)所示。激光飞行距离等于光速乘以激光脉冲回波接收时间和激光脉冲触发时间之间的时间差的一半。

4 成像仿真结果

本文仿真的激光雷达探测目标的灰度二维图像如图13(a)所示。目标图像的像素数为76×138。目标图像中一个像素的灰度值表示激光雷达与该像素点之间的距离。假设激光雷达图像的像素数为38×69,采用平均法得到理想的激光雷达图像,如图13(b)所示。信噪比用于控制杂波干扰的模拟杂波输入强度。分别使用CFD算法,小波变换算法和复合算法生成激光雷达图像。模拟图像和理想图像之间的均方误差(MSE),用以评估杂波识别算法的性能。

图13 激光雷达探测目标灰度图像和理想图像

图14给出了SNR=5时分别使用CFD,小波变换,复合算法生成的图像与误差图,激光雷达图像与理想图像的绝对距离误差如图14右侧所示。并与传统的匹配滤波,CFD与匹配滤波的复合算法生成的图像比较,如图15所示,CFD与小波变换的复合算法的生成图像的均方误差MSE最小,该算法性能更好。

本文提出使用新型的阈值函数进行小波变换。图16展示了SNR=5时改进的小波变换与CFD的复合算法生成雷达图像与误差图。由图中可以看出,改进的小波变换生成的雷达图像的误差更小,有更好的成像性能。

图16 CFD与新型小波变换复合算法生成的图像

三种算法的成像性能呈现出不同的变化趋势。仿真图像MSE趋势图随信噪比变化如图17所示。当SNR<6时,小波变换比CFD的均方误差更小。CFD算法是利用接收脉冲触发时间测量,接收脉冲在信噪比过小时受到杂波的严重干扰,小波变换可以在去噪的同时提取信号的特征。因此信噪比较小时,小波变换在杂波严重的环境中更容易检测到信号,有更好的成像性能。CFD与小波变换的复合算法生成的图像的MSE远远小于CFD和小波变换的MSE,复合算法具有更好的成像性能。

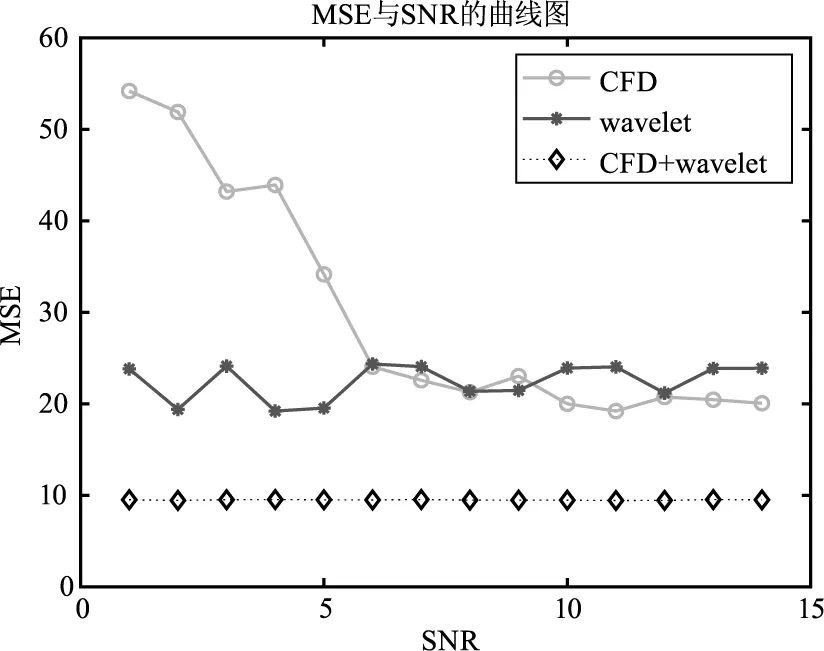
图17 CFD与新型小波变换复合算法生成的图像

本文提出的一种改进的小波变换与CFD相结合生成雷达图像方法,和小波变换与改进的小波变换方法的MSE结果如表1所示。改进的小波变换的雷达图像的均方误差小于小波变换的雷达图像的均方误差,证明了改进的小波变换与CFD结合的复合算法具有更好的成像性能。

5 结 论

本文利用由激光脉冲发射、杂波干扰、激光脉冲接收和生成目标图像构成的仿真模型,提出了CFD与小波变换的复合算法进行雷达成像,分别使用恒比鉴别算法,小波变换算法,恒比鉴别和小波变换的复合算法生成激光雷达图像。与传统的匹配滤波,CFD与匹配滤波的复合算法比较,证明CFD与小波变换的复合算法有更好的成像性能。同时为了进一步提高新复合算法的性能,提出了一种基于新型的阈值函数的小波变换算法与恒比鉴别结合,新型的小波变换具有更好的成像性能。对雷达图像处理有借鉴意义。