城市道路平面交叉口复杂度研究进展

郭凤香, 熊昌安

(昆明理工大学交通工程学院, 昆明 650500)

经济迅速发展为车辆的发展带来了巨大增长空间的同时,也给城市交通带来了巨大的压力,城市道路平面交叉口往往由于内部交通组成的复杂多样,使其接近工作负荷的上限,进而导致道路乃至整条路网无法充分发挥功能效率,制约其服务水平。在现实生活中判别城市道路平面交叉口的工作负荷常依据服务水平划分,然而事实上二者之间并无直接量化关系,直接依据服务水平对交叉口的运行状态进行评估缺乏合理性[1]。如何高效筛选交叉口的信息,创建合理评价交叉口运行状况的模型,以提高交叉口功能区的安全水平和通行效率,降低交通拥堵刻不容缓[2-6]。

复杂度理论研究的快速发展,使其在城市交通领域也得到了广泛应用[7]。吴建军等[8-9]、李树彬等[10]将用户平衡配流与复杂网络相结合,分析城市交通网络的复杂性；何兆成等[11]创建了基于大规模浮动车数据的城市路网复杂度分析方法,将“路段置信点”引入城市路网中。为解决交通信息采集时浮动车等间距采样的不足,曹闻等[12-13]提出基于城市道路复杂度的自适应采样算法；岳小泉[14]采用交通冲突技术评估交织区的安全性；许源[15]应用“车公里冲突数”这一运行参数作为交织区的安全评价指标；杜胜品等[16]通过构建计算交织区复杂度和车道复杂度的静态模型,对交织区内各车道不同流向之间的相互干扰程度进行了定量描述；Addison等[17]、Nair等[18]和Johanns等[19]采用分维、李雅普诺夫指数和测度熵等特征量刻画交通流的复杂性；张美坤等[20]引入统计复杂度对实测交通流进行复杂性测试,解决了交通流系统复杂性测度的可比化问题；刘峰涛等[21-22]为量化交通流系统的复杂度,在张美坤等[20]研究的基础上进一步引入了近似熵这一特征量；Gao等[23-24]、Li等[25]利用Nash模型模拟交通流的演化,将交通流状态与复杂网络通过元胞自动机模型相结合,提出了一种基于交通流演化的进化网络,并进行了深入研究；李巧茹等[26]采用节点收缩法量化了网络结构特性对交通阻抗的影响；吕文红等[27]、潘福全等[28-32]对公路信号平面交叉口的交通状况进行研究,提出了交叉口的“交通冲突”和“安全服务水平”两个概念,并对交通冲突的类型和影响交叉口运行状况的因素进行了细致分类；Wu等[33]通过研究车辆跟驰过程中加入扰动后产生的时间序列,构建了交通流状态与网络拓扑的对应关系。

邓加兴[34]从动态交通流与静态交通设施两个角度综合考虑交叉口的空间布局(静态)和交通流量(动态)对交叉口运行状态的影响,构建基于几何与流量叠加的城市道路平面交叉口复杂度分析模型,更加合理地量化城市道路平面交叉口的运行状态；Fisherlison[35]依据机动车与机动车之间在交叉口产生的交通冲突点的种类和数量,提出交叉口综合复杂性系数,并初步建立交叉口复杂程度等级划分标准；王炜等[36]按照中国的实际情况对交叉口综合复杂性系数模型进行了调整与优化,使之更加贴合中国的交通状况；东南大学利用系统分析方法对交叉口复杂度进行深入研究,构建了平面交叉口综合复杂性系数AHP(analytic hierarchy process)分析模型；刘飞[37]归纳总结了交叉口各类交通冲突点数量的正确统计方法,为描述交叉口的运行状态,构建基于冲突形式和交通方式的交叉口复杂度计量模型；沈家军等[38-41]提出交叉口复杂度的概念及其内涵,综合考虑宏观和微观两个层面对交叉口运行秩序的影响,构建基于冲突点数量和冲突概率的交叉口复杂度计量模型；周娇[42]认为交叉口复杂度是各类冲突点数量与产生冲突的车流在该点处发生冲突的概率的乘积加权之和,针对沈家军提出的模型进行精炼和简化,增加了模型的实用性；李文勇等[1]借鉴费舍里松所提出的交叉口复杂度静态模型,创建了交叉口静态秩序模型和交叉口动态秩序模型,量化了交叉口的交通拥堵产生率。但是上述研究关于城市道路平面交叉口复杂度研究的产生、发展等研究进展,仍缺乏较为系统的总结和梳理。

鉴于针对城市道路平面交叉口复杂度的产生、发展等研究进展仍然缺乏较为系统的梳理,拟对中外交通领域中有关城市道路平面交叉口复杂度的相关定义、内涵和计量模型进行系统介绍,使读者对此问题有一个相对全面的了解,并基于当前的研究现状分析研究中的不足之处及后续发展趋势,以期促进相关研究的深入开展。

1 交叉口复杂度定义

“复杂性科学”这一概念于20世纪80年代被明确提出,外国有学者认为该科学的研究对象分别为复杂系统和复杂性[43]；但针对复杂性科学的研究起步较晚,且各领域的研究对象各不相同、方法各异,故关于如何定义复杂性科学与复杂系统尚未达成共识[44-45]。钱学森[46]认为复杂性是开放的复杂巨系统的动力学特征；Trappl[47]认为复杂性人工自制的自然系统中仅能掌握其中部分机理,无法完全理解的性质；西蒙[48]则认为一个系统的复杂程度,取决于人们对它采取何种描述方式；成思危[49-50]认为复杂性科学的研究核心是揭示客观事物构成及其演化历程,预测其发展趋势。

交叉口复杂度是交通领域的新兴概念,针对这一概念的深入研究相对较少,最早可追溯到20世纪80年代，苏联学者Fisherlison[35]提出的交叉口综合复杂性系数,对交叉口的复杂性程度进行定量描述；刘飞[37]在宏观层面对交叉口复杂度给出定义,他认为交叉口复杂度是一个可以度量交叉口的运行组织和空间布局的复杂性程度的量化指标；沈家军[38]综合考虑宏观和微观两个层面对交叉口运行秩序的影响,他将交叉口复杂度定义为综合性衡量指标,该指标能够量化交叉口的空间布局及运行组织的有序性,度量交叉口交通冲突点及冲突概率,反映不同类型交通流各自的运行特征。

综上所述,交叉口复杂度不仅与交叉口的交通冲突和空间布局有关,同时也与经过交叉口功能区的交通流息息相关[51-53],能够合理、准确地评价交叉口功能区的空间布局和运行组织的合理性,综合反映不同类型交通流途经交叉口时各自的运行状态。

2 城市道路平面交叉口复杂度计量模型

目前用来评估城市道路平面交叉口复杂度的模型主要分为静态模型和动态模型两类。静态模型仅考虑交通冲突和交叉口几何形状对交叉口复杂度的影响,主要包括由费舍里松提出并经徐吉谦改良的交叉口复杂度静态模型、平面交叉口综合复杂性系数AHP分析模型、基于冲突形式和交通方式的交叉口复杂度计量模型；动态模型从交通冲突、交通量和交叉口静态布局三方面综合考虑交叉口复杂度对交叉口运行状态的影响,主要有基于冲突点数量和冲突概率的交叉口复杂度计量模型、基于冲突点数量和冲突概率的交叉口复杂度简化模型和叠加流量流向的平面交叉口复杂度分析模型3种。关于交叉口复杂度研究的发展过程如图1所示。

图1 交叉口复杂度计算模型发展过程Fig.1 Development process of intersection complexity metrology model

2.1 静态模型

静态模型主要从冲突点数量和不同交通方式之间的冲突概率两方面着手分析交通冲突对交叉口复杂程度的影响,主要包括3种模型,分别为:交叉口复杂度静态模型[35]、平面交叉口综合复杂性系数AHP分析模型[36]和基于冲突形式和交通方式的交叉口复杂度计量模型[37]。但静态模型未能认识到交叉口的交通流量大小也会对交叉口的复杂度产生影响,无法准确评价交叉口的运行状态,存在一定的局限性:当交叉口的交通组成较为单一、不同交通方式之间的冲突点数量较少,但若通过交叉口的交通流量十分巨大,则交叉口的复杂程度也会随之增加,当交通量超过交叉口所能允许的最大通行能力时,将导致交通堵塞,对来往车辆的正常通行造成严重干扰。

2.1.1 交叉口复杂度静态模型

交叉口复杂度静态模型[35]由苏联学者Fisherlison于20世纪80年代提出。Fisherlison认为在任何一个没有人为干预的交叉口,必然会出现车流交叉、合流和分流现象；其中危险程度按从大到小的顺序依次为车流交叉、车流合流和车流分流,采用换算系数将三类车流冲突点的复杂性纳入总体评价系统,定义分流点的系数为1,合流点的系数为3,交叉点的系数为5,建立交叉口复杂程度的静态模型,可表示为

C=n0+3nc+5nn

(1)

式(1)中:C为城市道路平面交叉口的复杂性系数；nc为机动车合流点数量；n0为机动车分流点数量；nn为机动车交叉点数量。如表1所示,Fisherlison将城市道路平面交叉口的复杂程度根据交叉口复杂度数值的大小分为4个等级。

表1 城市道路平面交叉口复杂程度分级Table 1 Urban road level intersection complexity classification

结合中国的交通现状,对Fisherlison提出的交叉口综合复杂性系数计算方法进行调整,使之更加贴合中国的实际情况，如式(2)所示:

C=k1nd+k2nm+k3nj+k4nw

(2)

式(2)中：nd、nm、nj、nw分别为各类冲突点的数量；k1、k2、k3、k4为冲突点系数。

交叉口复杂度静态模型将交通冲突点作为影响交叉口复杂程度的重要因素,对其进行定量描述,为评估交叉口的运行状态提供了一种全新的角度,仅适用于初步评估常规城市道路平面交叉口(十字形交叉口、T形交叉口等)的运行状态,无法应用于畸形交叉口和环形交叉口评估。但该模型不具备实用性,模型将交通冲突点的数量定义为决定交叉口复杂程度的唯一影响因素,未考虑到冲突概率的存在,且模型中仅分析了机动车交通流之间产生的冲突,对交通冲突点类型的考虑过于单一,未考虑非机动车和行人对交叉口运行的影响,严重脱离实际情况,无法准确衡量城市道路平面交叉口的实际运行状态；且模型中关于不同类型交通冲突点对交叉口影响程度之间的量化关系过于简单,未经过实际调查,仅为Fisherlison基于个人经验提出,未就交通流微观运行特征对交叉口复杂度产生的影响加以考虑。

王炜等[36]仅对交叉口复杂度静态模型进行细微的调整与改进,使之更加适合中国当时的交通现状,未给出冲突点系数的具体取值方法,依然将冲突点数量定义为决定交叉口复杂程度的唯一影响因素,未考虑流经交叉口的交通量对交叉口交通运行复杂程度的影响,忽视了在冲突点数量保持不变的条件下,交叉口运行状态的复杂程度仍会随交通量的增加而增加这一关键因素,不符合交叉口的实际运行情况。

2.1.2 平面交叉口综合复杂性系数AHP分析模型

东南大学利用系统分析方法对交叉口复杂度进行了深入研究,构建了平面交叉口综合复杂性系数AHP分析模型[36],可表示为

(3)

式(3)中:Rij为第i个因素对第j个方面的权重;Pj为第j个方面的权重;αij为交叉口第i个因素对第j个方面的影响分值。

该模型在交叉口复杂度静态模型的基础上进一步考虑了交叉口中3个方面、11个因素对交叉口复杂度的影响,增加了平面交叉口复杂度影响因素的范畴；该模型适用于周边环境复杂且对交叉口运行产生较大影响的常规城市道路平面交叉口工作负荷的初步评估。但模型中评价指标数量巨大且多为定性成分,在实际应用时会造成工作量巨大且难以统计完全,未涉及各评价指标系数的分析方法及求解过程,难以确定评价指标的权重,对模型计算的准确性产生了干扰；同时,该模型在建立时未将交通量对交叉口交通运行复杂程度的影响这一关键因素纳入考虑范围,严重忽视了在冲突点数量保持不变的条件下,交叉口运行状态的复杂程度仍会随交通量的增加而增加。该模型已不适用于评估常规城市道路平面交叉口的工作负荷与运行状态,更无法应用于评估畸形交叉口和环形交叉口的工作负荷。

2.1.3 基于冲突形式和交通方式的交叉口复杂度计量模型

刘飞[37]归纳总结了城市道路平面交叉口各类交通冲突点数量的正确统计方法,从基于不同冲突形式和不同交通方式产生的交通冲突点数量分别建立了交叉口复杂度计量模型。

(1)基于不同冲突形式，有

C=k′1Nj+k′2Nm+k′3Nd

(4)

式(4)中：k′1、k′2、k′3依次为交叉、合流和分流3种冲突点的权重系数；Nm、Nj、Nd依次为合流、交叉和分流3种冲突类型的冲突点数量。

(2)基于不同交通方式，有

C=ka-aNa-a+ka-bNa-b+kb-bNb-b

(5)

式(5)中：ka-a、ka-b、kb-b依次为机动车与机动车之间的冲突点系数、非机动车与机动车之间的冲突点系数和非机动车与非机动车之间的冲突点系数；Na-a、Na-b和Nb-b依次为机动车与机动车之间的冲突点数量、机动车与非机动车冲突点数量、非机动车与非机动车之间的冲突点数量。

该模型针对十字形城市道路交叉口典型的两相位信号控制方式和四相位信号控制方式进行研究,故模型仅适用于十字形城市道路交叉口的复杂度计算,未涉及其他类型的城市道路平面交叉口如T形、环形等。模型从冲突形式和交通方式两个方面考虑城市道路平面交叉口的复杂度,扩展了影响交叉口复杂程度的交通冲突点的种类,更加准确地描述了十字形城市道路交叉口的复杂程度；但该模型对合理评判交叉口复杂度的认识仍停留在交通冲突点数量上,未考虑交通流微观运行特征对交叉口运行状态的影响和交通量对交叉口复杂程度的影响,未详细标定模型中各个参数的取值。

2.2 动态模型

交叉口冲突点按类型可分为机动车冲突、机-非冲突、行人与机动车冲突、非机动车与行人冲突、非机动车冲突及行人之间的冲突6类,其中前3类交通冲突对交叉口运行产生的影响较大[54],故目前针对交叉口交通冲突点的研究多以这3类交通冲突点为主,并产生了一大批科研成果[55-61]。动态模型从交通冲突、交通量和交叉口几何形状三方面考虑交叉口复杂度对交叉口运行状态的影响,弥补了静态模型忽略了交通量对交叉口复杂度的影响这一缺点,能够更加准确、合理地评价城市道路平面交叉口的运行状态。主要研究成果包括3种,分别为基于冲突点数量和冲突概率的交叉口复杂度计量模型[38,62]、基于冲突点数量和冲突概率的交叉口复杂度简化模型[42]和叠加流量流向的平面交叉口复杂度分析模型[34]。

2.2.1 基于冲突点数量和冲突概率的交叉口复杂度计量模型

Hossain[63]认为行人、机动车和非机动车三要素是组成交叉口混合交通流的基本条件。沈家军等[41]以机动车冲突、行人与机动车冲突和机动车与非机动车冲突为研究对象,综合考虑宏观和微观两个层面对交叉口运行秩序的影响,如式(6)所示,搭建了基于冲突点数量和冲突概率的交叉口复杂度计量模型:

(6)

该模型以交通冲突作为衡量交叉口复杂度的核心指标,将交通流微观运行特征纳入影响交叉口复杂度的因素中,用冲突强度衡量交通冲突的严重程度,考虑冲突点数量和冲突概率两个方面对交叉口运行状态的影响,进一步提升了模型的准确性；但该模型中按机动车、非机动车、行人3类交通参与者和直、左、右3个交通流向统计所有类型的交通冲突点,冲突点种类过于全面,涉及的交通流微观参数过多且难以测量,虽增强了模型的准确性,但在一定程度上限制了模型的实用性。该模型仅适用于评估常规城市道路平面交叉口的工作负荷与运行状态,如十字形、T形等交叉口。

2.2.2 基于冲突点数量和冲突概率的交叉口复杂度简化模型

周娇[42]认为交叉口复杂度是各类冲突点数量与产生冲突的车流在该点处发生冲突概率的乘积加权之和,对沈家军等[38-41]提出的模型进行了精炼和简化,通过分析行人、非机动车和机动车三者之间产生冲突的概率以增加模型的实用性，可表示为

C=C1+1.3C2+1.7C3

(7)

(8)

(9)

(10)

(11)

式中:C1为机动车冲突复杂度;C2为机动车与非机动车冲突复杂度;C3为行人与机动车冲突造成的复杂度;pjdi和pjmi依次为分流冲突点、合流冲突点处折减前的平均冲突概率；pji为交叉冲突点的平均冲突概率；在计算pjdi和pjmi时,将产生冲突的两类交通流中的主要交通流代入QP,次要交通流代入QS；Nj、Nd、Nm依次为交叉、分流、合流三类冲突点的数量；pj2为机动车与非机动车交叉冲突点处的平均冲突概率；Q1为机动车交通量，pcu/min；Q2为非机动车交通流量，pcu/min；Nj2和Nj3分别为机动车与非机动车冲突点的数量、行人与机动车冲突点的数量；pj3为机动车与行人交叉冲突点处的平均冲突概率；Q3为行人流量，人/(m·min-1)。

基于冲突点数量和冲突概率的交叉口复杂度简化模型以冲突流量为自变量,减少了模型中涉及的交通流微观参数数量,简化了计算交叉口复杂度的步骤,增加了模型的实用性；但模型中将机动车交通与慢行交通的冲突区域默认为点,对机动车交通与慢行交通冲突区域的模糊定义导致该模型在准确反映交叉口的实际运行情况上存在一定偏差。较之基于冲突点数量和冲突概率的交叉口复杂度计量模,该模型更加适用于评估常规城市道路平面交叉口(十字形交叉口、T形交叉口)的工作负荷与运行状态,但该模型无法对非常规城市道路平面交叉口(如畸形交叉、环形交叉口等)的工作状态进行有效评估。

2.2.3 叠加流量流向的平面交叉口复杂度分析模型

邓加兴[34]从基于流量流向的机动车-机动车冲突的复杂度和基于机动车与非机动车冲突及机动车-行人的冲突两方面分析城市道路平面交叉口复杂度,在Fisherlison静态模型的基础上进一步提出了叠加流量流向的交叉口复杂度分析模型,可表示为

C=l1C1+l2C2

(12)

(13)

(14)

(15)

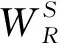
该模型纠正了静态模型中单纯以冲突点为交叉口复杂度衡量标准、忽视交通量对交叉口复杂度影响的缺点；将交通量纳入模型的考虑范畴。但该模型的构建尚存在较大缺陷,研究者未能很好地对前人的研究内容进行有效总结,模型中的冲突点系数仍采用Fisherlison[35]所提出的数值,冲突系数的取值与实际情况严重不符,未考虑交通流微观运行特征对交叉口产生的影响,导致该模型欠缺实用性。该模型更加适用于评估常规城市道路平面交叉口的工作负荷与运行状态,如十字形交叉口、T形交叉口等。各种交叉口复杂度计量模型优缺点,如表2所示。

表2 交叉口复杂度计量模型比较Table 2 Comparison among models of measuring intersections’ complexity

3 结论与展望

总体来说,中外在城市道路平面交叉口复杂度方面的研究日趋完善与成熟,也越来越趋向于应用型研究。但目前针对交叉口复杂度的研究水平还无法满足合理、准确评价城市道路平面交叉口的交通运行状态的迫切需求。通过前述分析,并考虑到未来可能的市场需求,城市道路平面交叉口复杂度的研究在以下4个方面仍值得加强。

(1)已有的各类道路平面交叉口复杂度计量模型中针对各类交通冲突点系数的确定方法存在较大局限性。如平面交叉口综合复杂性系数AHP分析模型、基于冲突形式和交通方式的交叉口复杂度计量模型和叠加流量流向的平面交叉口复杂度分析模型均未能给出冲突点系数的详细标定方法。目前对于模型中各类交通冲突点权重占比的研究未能充分考虑各种影响因素,无法准确得出冲突点在模型中的权重占比和各类冲突点之间的量化关系,除了在基于冲突点数量和冲突概率的交叉口复杂度计量模型中,研究者创造性地提出以冲突概率作为冲突点系数,初步解决了冲突点系数(模型参数)难以标定的问题,但未考虑交叉口周边环境(如天气、噪音的分贝数等)对交叉口交通冲突的影响[36],在接下来的研究中应结合交叉口所处的环境对模型参数的确定进行调查研究。

(2)当前研究学者们所提出的交叉口复杂度计量模型大多仅适用于十字形等常规城市道路交叉口,无法对环形交叉口这类特殊交叉口的复杂程度进行评估,应对环形交叉口的交织区复杂度进行量化研究,建立复杂度计量模型。交织区是环形交叉口的重要组成部分,车辆在交织区的换道行为是环形交叉口发挥作用的核心,不同类型的交通流在逆时针绕岛运行中仅产生合流冲突与分流冲突,与常规城市道路交叉口的冲突类型迥异,车流在交织区范围内随机选择车道变更路线,因此环形交叉口不同车流之间的冲突点并非存在于固定位置,而是充斥在整个交织区中,且环形交叉口的冲突点种类严重影响了环岛交织区的复杂性和不同类型交通流之间的相互干扰程度,故现有交叉口复杂度计量模型难以有效评估环形交叉口的复杂度。综上,基于冲突点进行环形交叉口交织区复杂度的量化研究将为交织区安全状况评价和通行效率研究提供评判标准。

(3)当前针对城市道路平面交叉口复杂度的相关研究仅停留在复杂度数值量化计算层面,在实际研究中,计算一个城市道路平面交叉口的复杂度,往往因为选择模型的不同导致计算结果产生巨大差异,除Fisherlison提出了交叉口复杂程度的初步分级外,中外尚未对各种类型城市道路平面交叉口复杂度建立起统一的复杂程度等级划分标准。为便于更加直观地理解“交叉口复杂度”这一概念、更好的理解交叉口复杂度与交叉口运行状态的内在联系,建立交叉口复杂度模型冲突点权重系数评价方法以完善不同类型城市道路平面交叉口复杂度的严重程度划分显得尤为重要。

(4)目前交叉口复杂度的研究尚未建立驾驶人行为与城市道路平面交叉口复杂度之间的联系。城市道路平面交叉口复杂度是一个综合性的评价指标,建立起交叉口复杂度和驾驶人行为之间的定量关系有利于辨识驾驶人行为差错、研究不同复杂程度下的驾驶人行为及生理心理特性、保障驾驶人出行安全、改善交叉口交通环境。探索交叉口复杂度与驾驶人驾驶行为之间的定量关系,使得交叉口复杂度能够更加准确反映交叉口运行状况对车辆驾驶人的影响是接下来城市道路平面交叉口复杂度的研究方向之一。

基于近年来中外交通领域中有关城市道路平面交叉口复杂度研究方面的重要研究成果,系统梳理了城市道路平面交叉口复杂度相关定义、内涵和计量模型,归纳了各种城市道路平面交叉口复杂度计量模型的优缺点,并在此基础上对未来的研究前景提出了展望。

由于城市道路平面交叉口复杂程度与交叉口的通行效率和安全密切相关,因此,有必要一方面加快关于城市道路平面交叉口复杂度的深入研究；另一方面建立交叉口复杂度与交叉口通行效率和安全之间的联系,并基于此提出合理划分交叉口复杂度等级的依据,更加合理的评价城市道路平面交叉口的运行状态。