砂砾岩地层三维地应力场研究
2021-04-07梁利喜刘向君户海胜钟自强
梁利喜, 高 阳, 刘向君, 户海胜, 熊 健, 钟自强
(1.西南石油大学, 油气藏地质与开发工程国家重点实验室, 成都 610500; 2.中国石油新疆油田分公司勘探开发研究院, 克拉玛依 834000)
某地区百口泉组砂砾岩地层岩性油气藏显示出巨大的勘探潜力,成为西部某油田重要的增储上产领域[1]。由于对该地区地应力特征认识程度较低,在油气开发过程中频现储层压裂改造效果差异大、水力压裂裂缝扩展延伸规律难以预测以及水平井井筒相继出现砂桥而堵塞流体通道等问题,因此迫切需要进一步研究该地区的地应力场状态,为完善井网部署、优化压裂设计、防治采油出砂等提供依据[2-3]。
地应力是自然状态下存在于岩体内部的应力,由岩体自重、地质构造作用及温度压力等共同作用下形成。随着油气勘探开发深度的加大,地质环境越来越复杂,地应力大小及方向对油气井工程、油气勘探开发等各个领域的重要影响越来越受到工业界的高度关注[4-5]。目前为止,中外学者研究地应力的方法,主要有构造形迹分析法、室内岩心测试技术、矿场实测分析、测井曲线计算法、物理和数值模拟技术等,并朝着多种方法综合应用、相互印证方面发展完善[6]。随着计算机科学的迅猛发展,数值模拟技术在地应力场研究中的应用愈加广泛,其能够较好地综合考虑深部地层岩石物理力学性质复杂多变、地层介质各向异性、非均质性、不连续性和复杂边界条件等因素,该方法受到了学者们的青睐[7-10]。目前,大多数的地应力场数值模拟反演文献的技术路线都是以单点地应力实测资料为约束与修正依据,通过试算法或者人工智能优化方法(BP神经网络、粒子群算法等)确定应力或位移状态边界条件,进而获得地应力场。然而在非均质性较强的砂砾岩地层中,地应力受地层岩性影响,单点地应力测试结果往往不能代表研究区域整体地应力状态。因此,以实测地应力数据点为基础,建立合理的地应力测井预测模型获取地应力剖面,从点到线对地应力的纵向分布特征进行研究,减小岩性对地应力结果的影响,增大了地应力场反演约束数据量。在此基础上,利用地震构造模型构建合理的三维空间数值模型,以单井地应力剖面计算结果为基本约束,利用有限元法进行地应力场的数值模拟反演,实现从线到体对工区地应力场进行研究,从而获取研究工区地应力的横向分布特征和纵向分布特征。
1 单井地应力测试分析
原始地应力测试就是确定存在于研究位置点及其周围区域的未受扰动的三维应力状态,包括地应力大小以及地应力方向两个方面。工区目的储层岩性为砂砾岩,物性条件差,一般都采用水力压裂来改造储层提高产能以达到工业要求。因此,采用资料丰富的压裂改造资料及地球物理测井资料分析深部地应力。
1.1 地应力大小
水力压裂资料反演地应力大小是深部地层应力测量最有效的方法,也是国际岩石力学测试技术委员会推荐的岩体应力测量的主要方法之一[11]。基于岩石为连续、均质和各向同性的假设,依据岩石力学分析和能量最低原则,水力压裂缝的起裂发生在井壁切向应力最小的部位,当井轴与垂直主应力方向一致时,裂缝的发育方位指示水平最大主应力方位。压裂过程中的裂缝闭合压力是缝面相互接触时的压力,此时裂缝深度已达原岩应力状态,故闭合压力反映水平最小主应力大小。从压裂施工动态变化曲线中可以读出破裂压力和闭合压力,根据式(1)可计算出水平最大主应力,其中岩石抗张强度、biot系数及地层压力均来自项目测试结果。
Pf=3σH2-σH1-αPP+St
(1)
式(1)中:Pf为破裂压力,MPa;σH2为水平最大主应力,MPa;σH1为水平最小主应力,MPa;α为biot系数;PP为地层孔隙压力,MPa;St为岩石抗张强度,MPa。
基于上述方法对研究区28个井段的压裂资料进行分析,分别获得压裂深度点的破裂压力和闭合压力,计算出对应的水平最大主应力和水平最小主应力。结果表明,水平最小主应力分布在32.54~74.59 MPa,平均值为56.49 MPa;水平最大主应力分布在37.48~99.91 MPa,平均值为70.17 MPa。
1.2 地应力方位
在钻井过程中,由于钻具震动、原始地应力释放、钻井液密度过大等原因会形成分布于井壁上的诱导裂缝,与地应力有关的重泥浆压裂缝和应力释放缝的方位都指示水平最大地应力方向。根据弹性力学理论分析,高应力作用下井壁附近在水平最小主应力方向产生应力集中,当切向应力超过井壁岩石抗剪强度时,井壁剪切破坏出现井眼应力崩落现象,崩落方位指示水平最小主应力方向。成像测井具有高密度采样和高分辨率的特点,可以有效识别钻井诱导缝和井眼崩落,获取水平主应力的方位[12-13]。基于地层微电阻率扫描成像(formation micro-scanner image,FMI)测井资料对研究工区内共6个井段的钻井诱导缝和井眼崩落进行方位分析,某井部分井段分析结果如图1所示。由图1可见羽状排列的应力释放缝组,指示该井水平最大主应力方位为NWW向,优势方位约为105°。

图1 诱导缝指示水平最大主应力方位Fig.1 The direction of horizontal maximum principal stress indicated by conducted fracture
在各向异性地层中,横波沿传播方向将分裂成两个速度不同相互垂直的子波(快、慢横波),这种现象叫横波分裂。井周地层受不同方向的水平地应力作用导致受压程度不同,沿水平最大主应力方向岩石受压程度最高,快横波的方位可以指示水平最大主应力的方向[14]。基于Sonic Scanner测井数据,通过提取快、慢横波方位信息,分析快、慢横波时差大小及能量差等各向异性指标,对工区12个井段进行水平地应力分析。图2为某井部分井段分析结果,结果表明该井段快横波指示的水平最大主应力方位为E-W向,优势方位为90°。

DTEM_FAST为快横波,μs/ft;DTSM_SLOW为慢横波,μs/ft;FSH_P1N0为快慢横波的方位,(°)图2 快横波指示最大主应力方位Fig.2 The direction of horizontal maximum principal stress indicated by fast shear wave
分别采用FMI、Sonic Scanner两种不同的成像测井资料,基于不同岩石物理力学理论分析得到不同井位的水平主应力方位。结果表明,工区水平最大主应力整体呈现E-W向。受局部构造作用影响,不同井位处水平最大主应力方位存在一定差异。
2 地应力纵向剖面计算
以地应力实测资料为基础,建立合理的地应力计算模型,利用地球物理测井资料进行地应力纵向剖面计算分析,是目前中外石油工业界研究地应力的常用方法[15-16]。
2.1 垂向地应力
地层垂向地应力由上覆地层重力引起,数值大小取决于地层深度与岩石体积密度,采用密度测井的积分进行计算,公式为

(2)
式(2)中:σV为垂向地应力,MPa;H0为测井起始点深度,m;ρ0(h)为未测井段深度为h点的密度,g/cm3;ρ(h)为深度为h点的测井密度,g/cm3;g为重力加速度,m/s2。
2.2 水平地应力
利用测井资料计算水平地应力依赖于合理的计算模型,目前常用的模型有Mohr-Columb模型、Matthews & Kelly模型、Anderson模型、Newberry模型、黄荣樽模型、组合弹簧模型等[17]。其中组合弹簧关系模型认为水平主应力是上覆地层压力和水平构造应力共同作用的结果,综合考虑了地层岩石力学特性、孔隙压力及构造作用对地应力的影响,在实际工程中应用广泛。模型计算公式为
(3)
式(3)中:μ为泊松比;E为岩石弹性模量,MPa;εH为沿水平最大主应力方向构造应变系数;εh为沿水平最小主应力方向构造应变系数。
根据地应力计算模型确定地层岩石力学参数和地层孔隙压力是获取地应力必需的基础参数。岩石力学参数由岩石力学实验数据建立模型,结合测井数据计算获取;地层孔隙压力获取基于有效应力理论,由实测资料及测井数据进行多元回归分析建模获得。构造应变系数εH、εh是开展地应力剖面研究的关键性参数,利用地应力测试结果,根据式(3)反演即可得到。研究工区块部分井构造应变系数计算结果如表1所示。

表1 部分井构造应变系数分析结果Table 1 Results of tectonic strain ratio in some wells
2.3 地应力剖面
采用式(2)及式(3)的组合弹簧模型,结合分层构造应变系数,利用全井岩石杨氏模量、泊松比、地层孔隙压力等参数,可计算得到全井的地应力纵向剖面(图3)。计算分析结果表明,研究区域垂向地应力梯度大小为2.27~2.37 MPa/100 m,水平最大主应力梯度大小为1.79~2.71 MPa/100 m,水平最小主应力梯度大小为1.74~2.15 MPa/100 m,应力状态类型整体表现为潜在正断型应力场,即3个主应力大小关系为σV>σH>σh。

GR为自然伽马,API;CAL为井径,in(1 in=25.4 mm);AC为纵波时差,μs/ft;DEN为密度,g/cm3;CNL为中子,%;RT为深电阻率,Ω·m;RXO为浅电阻率,Ω·m;U为单轴抗压强度,MPa;E为弹性模量,MPa;PP为地层孔隙压力,MPa/100 m;SVC为垂向主应力,MPa/100 m;SHMG为水平最大主应力,MPa/100 m;SHNG为水平最小主应力,MPa/100 m图3 某井地应力纵向剖面图Fig.3 The profile of in-situ stress in a well
3 地应力场数值模拟
3.1 数值模型
地应力场与区域地质构造、地层岩石物理力学特性密切相关,地质模型的构建和岩石力学参数的赋值是地应力场反演的关键。由于地下深部构造复杂多样,考虑到计算工作量和计算精度,在深入认识研究区构造格架的基础上,对实际地质模型进行合理的抽象简化,基于已有的地球物理勘探资料地震解释数据体,建立了图4所示的三维数值模型。模型构建过程中充分考虑目的层的展布特征和起伏特性,并对研究工区8条规模较大的断裂破碎带进行重点描述。模型范围对应的大地坐标为X(15 409 580~15 436 580)、Y(5 095 665~5 110 665)。模型面积为27×15=405 km2,采用八节点四面体单元进行网格离散划分,经离散后模型共有节点85 721个,单元696 886个。

图4 研究工区目的层三维数值模型Fig.4 3D numerical model of the target formation
3.2 参数赋值
反演地应力场采用的是线弹性本构模型,需要对地质体的岩石力学参数(杨氏模量、泊松比)和体积密度赋值。传统数值模拟中力学参数的赋值往往将介质假设为均值体,而这往往导致分析结果的误差较大,故采用构建测井预测模型获取岩石力学参数的方法[18]。因此,通过室内三轴压缩试验得到岩样的静态岩石力学参数,通过纵、横波测试实验得到岩样的声波时差等物性参数,再利用静态力学参数与声波时差等物性参数做数理统计法拟合获得岩石力学参数测井预测模型,结合测井资料,获得岩石力学参数的纵向剖面。在此基础上,利用地震速度场三维数据体,使用井震联合技术,建立岩石力学参数的空间分布特性[19],为地应力场反演提供岩石力学参数赋值基础。由于研究工区内断裂带岩石松散破碎,无法取样测试,因此按照行业常用方法,将断裂带岩石力学参数按照一定比例降低[20],取用相应空间位置点岩石的2/3。
3.3 数值模拟反演分析
有限元模型建立后,以实测地应力方向为指导,对模型东侧和北侧设置模型边界荷载作用,并在模型西侧、南侧和底面设置法向位移约束以防止刚性漂移。合理确定施加边界后,以工区地应力测试及测井计算地应力大小和方向作为约束和修正依据,采用线性叠加原理反复修改边界条件直到误差最小,对地应力场进行多次正演和反演试算,最终确定合理的应力加载方式,并得出研究工区现今应力场的真实情况。
图5(a)~图5(c)分别为数值模拟计算得到的研究工区砂砾岩目的层的水平最大主应力、水平最小主应力以及垂向主应力的三维空间分布图。由图5可见,研究工区整体处于压应力作用下,垂向主应力分布在35~90 MPa范围内,水平最大主应力分布在40~80 MPa范围内,水平最小主应力分布在40~70 MPa范围内。受地层埋深和空间起伏影响,地应力整体呈现由西北向东南逐渐增大的趋势,地应力状态从局部走滑型(σH>σV>σh)逐渐转变过渡为整体正断型(σV>σH>σh)。工区断裂破碎带3个主应力较低,而断裂带附近垂向主应力、水平最小主应力变化较大且存在局部高应力带,此特征在C5、C6、C1井旁的北东向断裂尤为显著,这与断裂带空间位置和形态有关。图6所示为数值模拟计算得到的工区地层水平最大主应力方位,可见整体水平最大主应力方位呈近E-W,范围为75°~95°。在断裂附近,地应力向断裂延伸方向偏转的趋势明显,表现为NE、NWW走向断裂附近地应力方位呈NE向,NNW走向断裂附近地应力方位趋于垂直断裂延伸方向。
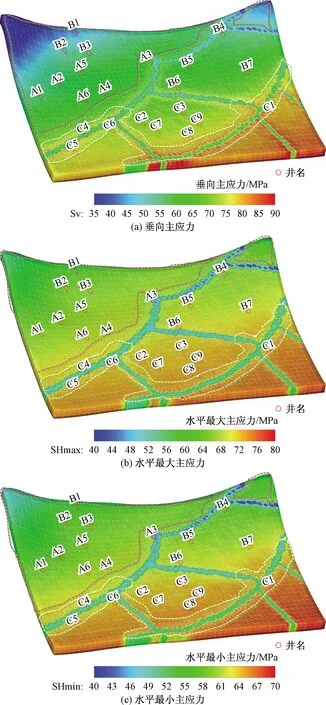
图5 三维空间分布Fig.5 3D space distribution

图6 水平最大主应力方位分布Fig.6 The azimuth of horizontal maximum principal stress
4 地应力场合理性验证
为验证地应力场模拟结果的合理性,使用研究区未参与约束和修正的5口井单点地应力测试资料与数值模拟计算结果进行对比,结果如表2所示。由表2可见二者的相对误差较小,说明数值模拟结果可以较好地反映本区块现今地应力场的三维展布特征。

表2 单井地应力测试结果与数值模拟结果对比Table 2 Comparison between experimental measurement results and numerical simulation results
研究区块构造格局形成于白垩纪早期。从区域构造演化历史来看,海西构造运动和印支构造运动对于研究区构造格局的形成起了至关重要的作用[21]。海西运动、印支运动造成西北缘地壳局部隆起,燕山期后冲断带格局基本形成,喜马拉雅运动后成为碰撞前陆型沉积坳陷。故三叠纪的印支运动产生S-N向的挤压应力,是研究区目的层现今水平主应力E-W方向形成的主要原因。工区主要发育两条NE向断裂,是次级断裂,与主断裂呈平行状态,其主要形成于海西构造运动时期,后在印支运动形成现今应力场的作用下,导致断裂附近地应力场方向沿着断裂偏转。因此,研究获取的工区地应力方向与区域构造背景状态相符。
5 结论
(1)基于丰富的压裂改造和地球物理测井资料,分析了研究工区已钻井目的层的实测地应力大小与方向,建立了适用于砂砾岩储层的地应力评价模型并计算了地应力单井纵向剖面。
(2)在地应力纵向剖面研究基础上,利用地震构造模型构建合理的三维空间数值模型,以单井地应力为基本约束,利用有限元法对工区现今三维地应力场进行反演。研究表明,工区地应力整体处于压应力作用下,表现为西北向东南方向逐渐增大的趋势。受断裂发育及次级构造影响,断裂内3个主应力显著降低,断裂边缘和端部存在应力激增带。地应力方位整体近E-W,受断裂和局部构造发育的影响,局部地应力方向发生偏转。
