微积分思想的不变性
2021-04-06毛战军
毛战军

【摘要】挖掘一元函数微积分思想与二元函数微积分思想的联系.讨论两类微积分中函数、极限、微分、中值定理、洛必达法则、牛顿—莱布尼茨公式等思想的不变性.
【关键词】一元函数;二元函数;思想;不变性
大学《高等数学》的内容中含有一元函数微积分学和多元函数微积分学,往往将其分置于教材的上、下两册中.在教学安排中,也往往将其分置于两个学期.学生在学习《高等数学》时,往往只能分别理解两者的思想,在学习多元函数微积分时感到困难.在教与学中,可以演绎一元函数微积分和多元函数微积分思想的不变性,使一元函数微积分思想有推广,多元函数微积分思想有衔接,把两者形成一个有机的整体.
多元函数微积分学往往以二元函数为代表来介绍其基本内容.这样,工作就放在了去发掘从一元函数微积分到二元函数微积分思想的不变性.下面就谈谈一元函数微积分和二元函数微积分中几个重要思想的联系.
1.函数的定义
函数的定义在形式上不变.
二元函数u=f(x,y),x∈D的自变量从点P0(x,y)变到P(x+Δx,y+Δy)的增量为(Δx,Δy),类比于一元函数的表示,在《高等数学》中不方便处理.而类比于一元函数,二元函数的自变量从点P0(x,y)变化到P(x+Δx,y+Δy)的增量是易于量化的,就是当自变量沿任意方向变化和沿坐标轴方向变化时的增量表示,这样就相应地产生了二元函数的方向导数及偏导数思想.
4.函數的微分
函数的微分中局部线性化思想不变.
通过对函数的(全)增量的表示进行解析,利用局部线性化的思想得到:一元函数的微分反映的是相应切线上点变化的特点;二元函数的(全)微分反映的是相应切平面上点变化的特点.
5.中值定理
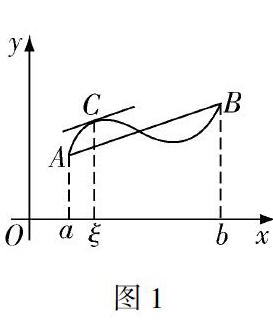
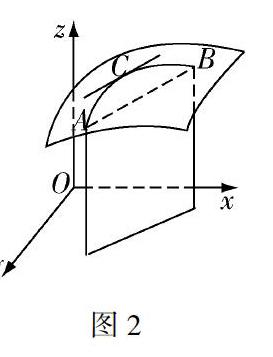
图1以拉格朗日微分中值定理为例,在坐标面与非坐标面上的量的关系不变.
在相应的条件下,如图1,一元函数的拉格朗日微分中值定理在几何上可以这样理解:在xOy面上,曲线弧AB上至少存在一点C,使得曲线弧AB在点C处的切线与弦AB平行.设曲线弧AB的方程为y=f(x),x∈[a,b],则点A(a,f(a)),B(b,f(b)),向量AB=(b-a,f(b)-f(a)),曲线弧AB在点C处的切向量为
6.洛必达法则
洛必达法则在公式形式上不变.
7.泰勒公式
泰勒公式用多项式来近似表示函数的思想不变.
8.定积分、重积分、线面积分
定积分、重积分、线面积分的“和式的极限”思想不变.
9.积分变限函数的微分
积分变限函数的微分公式的形式不变.
10.积分中值定理
积分中值定理形式不变.
11.牛顿—莱布尼茨公式
牛顿—莱布尼茨公式化为原函数的增量的思想不变.
12.结束语
通过对一元函数微积分与二元函数微积分相关思想的对比,可以发现:从一元函数微积分到二元函数微积分并不是另起炉灶的新思想,可以认为是同一思想在不同条件下的结论.在教与学中,如果在思想上能够对所学内容统一,那么可以使学生的学习视野更宽广,为学生学习专业课和向更高层次冲刺打下良好的基础.
【参考文献】
[1]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:58.
[2]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:60.
[3]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:133.
[4]覃淋.多元函数LHospital法则及其应用[J].保山学院学报,2017(5):36-40.
[5]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:139.
[6]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:122-123.
[7]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:238-239.
[8]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:212.
[9]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:234.
[10]同济大学数学系.高等数学(下册):第七版[M].北京:高等教育出版社,2014:240.
