数学情感在问题解决中的作用与路径

林炜 王伟

影响数学问题解决的认知要素

问题解决是一项认知的活动，这一过程中包含了一系列的认知因素：如记忆、意识、元认知、认知策略等，这些认知要素在理论上都与数学情感有着密切的关系。因此，问题解决中数学情感的研究，也可看作是基于认知理论的情感研究。

记忆与情感表征。记忆及表征过程在问题解决中扮演着重要的角色。但是相当长一段时期数学教育领域所关心的话题都集中在表征类型（如划分为代数和几何部分分别表征）、问题解决的策略（如列举、画图等），较少关注情感对储存和提取过程的影响，然而这两个概念在数学问题解决的过程中是非常重要的。如对长时记忆的提取在问题解决中体现在是否能将新的问题连接到已有的知识当中去，信息提取失败是阻碍顺利解决问题的一大绊脚石。在储存与提取的过程中，情感有没有起到作用，还有待进一步的论证。

意识在问题解决中的作用。研究者们对意识的关注是源于行为主义转向信息处理理论的发展，心理学家曼德勒指出，意识概念的出现其实是基于对人类信息处理重要性的关注，如果没有意识的存在，人类处理信息的能力及提取长期记忆的能力将会受到相当的限制。学者Rigney提出，在问题解决中，人类的意识应当属于情感因素中的重要部分。主要是因为意识与无意识心理过程有明显的区别，在对比了意识到有限能力与无意识的工作记忆后，发现在意识过程比无意识过程要慢。也有学者表明，意识对问题解决过程中的短时记忆有明显作用，至少在信息提取过程中发挥了一定分量的作用。因此，进一步研究意识在问题解决中的作用，有可能会指向意识与无意识的平行结构同步进行。

元认知在问题解决中的作用。学者舍费尔德认为，元认知对问题解决是极有帮助的，因为它可以帮助问题解决者决定采用何种策略、尝试此种策略多长时间，以及停止和替换另一种认知策略的时机等。如果我们帮助问题解决者自我反思他们的认知处理过程，就是将他们的情绪反应作用于问题解决。持续关注学生的情绪影响，能给予他们更强有力的认知过程控制。

自动化在问题解决中的作用。工作记忆或是意识本身的局限性，决定了在问题解决中频繁出现的心理过程自动化现象。此时个体的意识和元认知将不再参与到问题解决中去。由于有时候自动化的过程与问题解决者所要行走的方向是背道而驰的，所以消除不良自动化反应，创造积极自动化反应也一度成为数学课程领域的热点。有些数学课程专门为发展学生的自动化反应而设计，使学生能自动地进入数学问题的思考中。

问题解决策略与数学情感。在数学问题解决的教学上，最经典的方法就是波利亚提出的启发式教学法，包括图表法、倒推法等各种方法。这些方法及其运用、研究一度都只集中在认知领域，几乎没有学者关注到情感上的影响。后期，也只有个别学者提到问题解决策略有引起学生情感变化的可能。如将一个复杂问题简化的时候，学生会感到更有信心去解决剩下的问题，这种过程中因为得到步骤成就的信心与最终问题得以解决的信心是没有区别的。在数学教育中，我们应该何时、如何处理学生问题解决的结果才能既保护学生继续解决问题的信心，又及时纠正认知错误呢？这是值得进一步探索的问题。

数学情感在问题解决中的理论模型

数学问题解决本意上说是认知领域的活动，但近年来一直有与数学情感结合起来研究的趋势。学者卡尔丁（Goldin）构建了一个情感表征系统与认知表征系统相结合的数学问题解决能力的模型。在此模型中，研究学生的数学情感定位于狭义的情绪性状态，而非广义的特质性态度等。这种狭义的、瞬间的、变化性的情感状态更易于研究者捕捉学生在解决问题过程中的感受，看清他们在储存和提取有用信息、操作监控、激发启发式过程等方面的细节。因此，此研究遵循两项约定：一是情感在担任表征功能的作用时，具有持续激发情感路径的可能性，并且能够构建个人的狭义情感状态与个体认知的互动关系;二是稳定的情感结构过于复杂，可以通过分解成部分路径的方式来分析，即以狭义情感表征路径来呈现情感与认知在数学问题解决中的关系。在此定义下的情感结构是可以用于标记和表征认知信息的。因此，情感表征系统应包括如下几个方面：第一，状态或感觉的内部结构;第二，能影响到其他表征系统的情感表征路径;第三，基于认知事件的情感转化路径。

卡尔丁构建的模型分为两大路径来看问题解决中所经历的数学情感，与问题解决过程中的情感状态和启发式结构相结合，从结构的有效性和反效性两方面分析数学情感路径。

数学问题解决模型对实践教学的启示

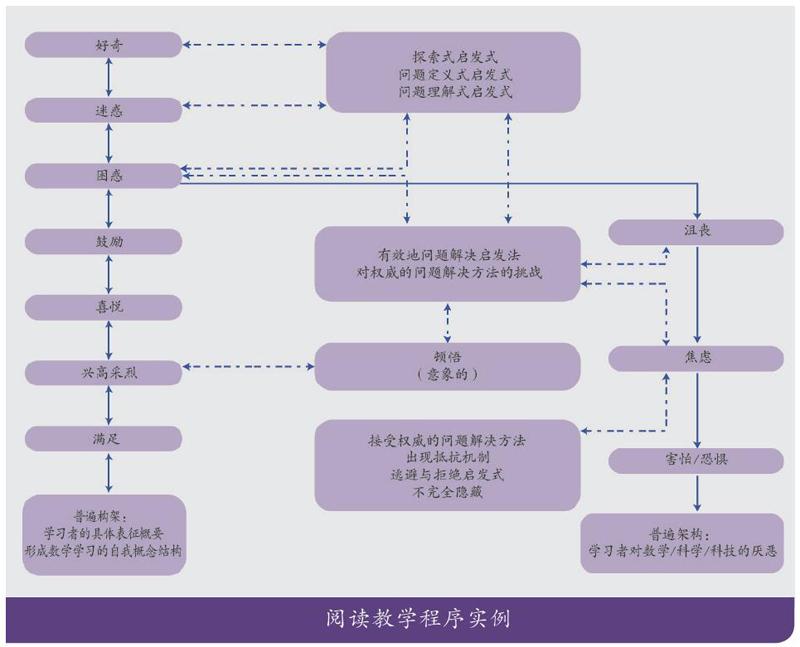
在卡尔丁构建的模型中，实线代表的是问题解决者个体改变可能经常会发生的狭义情感的路径;虚线代表的是问题解决过程中个体的情感状态可能会影响到启发式方法策略的路径。在这个理想化的模型中，问题解决者的情感状态都起源于好奇心。对学生来说，问题太深，他们就会产生迷惑的感觉，从而说明他们心里觉得没那么快能解开起初好奇的疑团。迷惑暂时还不会给问题解决个体带来负面情绪，但是当迷惑持续下去，个体就会产生困惑的感觉。学生会感觉解决这个问题像大海捞针，脑子一片空白、混乱。许多学生到这里就停滞了，难以继续，需要教师干预和帮助指导，才能渡过难关。在教师的指导和鼓励下，学生慢慢能解开疑团，疑难的问题开始被分解难度，学生之前的困惑慢慢转变成正向的喜悦之情。如果在教师的提示下，学生自我顿悟了某些节点，还可能给他们带来莫大的快乐。最终，他们能感受到问题解决的成功和满足，为进一步解决其他数学问题奠定了良性的心理基础。

但是，在困惑的阶段，有的学生可能会选择（或者教师为学生选择）自己继续往下走多一点。走的过程中可能给他们带来的感受是继续堆积的负面情绪越来越强烈，持续不断的停滞不前让他们感到沮喪，此时的问题解决者像钻进了一个死胡同一样。有可能下一步会突发一种新的思路或方法，把问题解决者带回到正能量主导的情绪状态中。也可能一直纠缠在问题无法解决的沮丧中，最终导致情感上的焦虑。如果此时还伴随着外部影响的效应，比如此次问题解决失败了，学生将会受到教师的批评或者获得很低的数学考试成绩，他们会把这种外部刺激内化到自身的情绪状态，最终害怕和恐惧，甚至是对数学这一门学科以及与它有关的学科的整体厌恶。

对于教育工作者而言，最大的挑战就是如何消除学生的消极情绪，如何重构与平衡认知与情感需求。无论如何，认知目标都应该建立在学生可以接受和操控的情感目标之下，数学情感应成为数学教育的基础性保障因素。