履带车辆传动系统主轴抗疲劳结构设计研究

王 成， 孙雪岩， 侯 威， 邹天刚， 杨啟福

(1. 中国北方车辆研究所车辆传动重点实验室，北京 100072；2. 江麓机电集团有限公司，长沙 411100)

传动轴是旋转机械系统传递动力和运动的关键零件，其使用性能对整个系统的功能实现和可靠性都起着至关重要的作用.运行过程中的传动轴承受交变载荷作用，疲劳是传动轴的主要失效形式，因此，针对传动轴疲劳问题开展研究具有非常重要的工程意义[1-2].

按照循环应力大小可将传动轴的疲劳类型分为高周疲劳(应力疲劳)和低周疲劳(应变疲劳).影响传动轴疲劳的因素主要包括外部载荷、结构参数、装配参数、材料特性和制造工艺，等等[3].目前，针对传动轴疲劳问题的研究集中在疲劳失效分析、疲劳寿命预测、抗疲劳制造和抗疲劳结构设计等方面[4-11].实际工程应用中，传动轴具有花键、润滑孔和过渡截面等复杂的结构特点，由结构突变引起的应力集中现象是造成局部应力过大的主要原因之一，严重影响传动轴的疲劳寿命.针对传动轴开展抗疲劳结构设计是降低工作应力，提高疲劳寿命的有效措施[8-9].另外，花键作为传动轴连接其他零件的主要形式，动力传递过程中，存在齿向载荷分配不均和齿根部位应力集中等问题，研究表明通过合理设计花键结构参数和载荷位置，可显著降低花键根部剪切应力和齿面接触应力[12-13].

本研究针对履带车辆综合传动系统主轴低周疲劳失效的问题开展抗疲劳结构设计研究，首先针对失效主轴材料开展力学性能试验，获得主轴材料的塑性变形阶段真应力应变关系；然后，在此基础上，以样车测试获得的冲击扭矩为输入，建立起步工况下主轴的弹塑性有限元模型，分别采用有限元法和解析法对比分析传动主轴的应力分布状态和应力集中系数，进一步研究主轴结构参数对最大应力和疲劳寿命的影响规律，所得结论为提高主轴的疲劳寿命和传动系统的可靠性奠定基础.

1 主轴材料弹塑性特性

某履带车辆传动系统主轴在起步工况下频繁发生低周疲劳失效，主轴疲劳断裂位置均发生在右侧，如图1所示，图中主轴中间花键为输入，两侧花键为输出.图2为产生初始裂纹的主轴，裂纹萌生于右侧输出花键与退刀槽交界位置的齿根处.将主轴疲劳样件裂纹打开，宏观形貌如图3所示，可见典型的疲劳弧线，属于疲劳断裂.

图1 主轴断裂实物样件

图2 裂纹位置

图3 裂纹断口宏观形貌

εT=ln(1+ε)，

(1)

σT=σ(1+ε).

(2)

式中：σ为工程应力；ε为工程应变.

主轴材料在屈服和缩颈之间为均匀塑性变形阶段，遵循幂乘关系硬化规律，真应力和真应变之间满足式(3)关系[10].

(3)

式中：K为循环强度系数；n为循环应变硬化系数.

对式(3)两侧取对数,得

lnσT=lnK+nlnεT.

(4)

由式(4)可知,lnσT和lnεT之间满足线性关系.

主轴材料采用300M钢，其杨氏模量为200 GPa，泊松比为0.3.针对5根主轴材料样件开展力学性能测试，结果如表1所示，其中，平均抗拉强度为1 865 MPa，平均屈服强度为1 575 MPa，平均断裂伸长率为11.5%，平均断面收缩率为46.2%.结合主轴材料拉伸力学性能曲线，确定屈服点的真应力εTY和真应变σTY以及缩颈点的真应力εTU和真应变σTU，从而确定循环强度系数K和循环应变硬化系数n[14]，结果如表2所示.

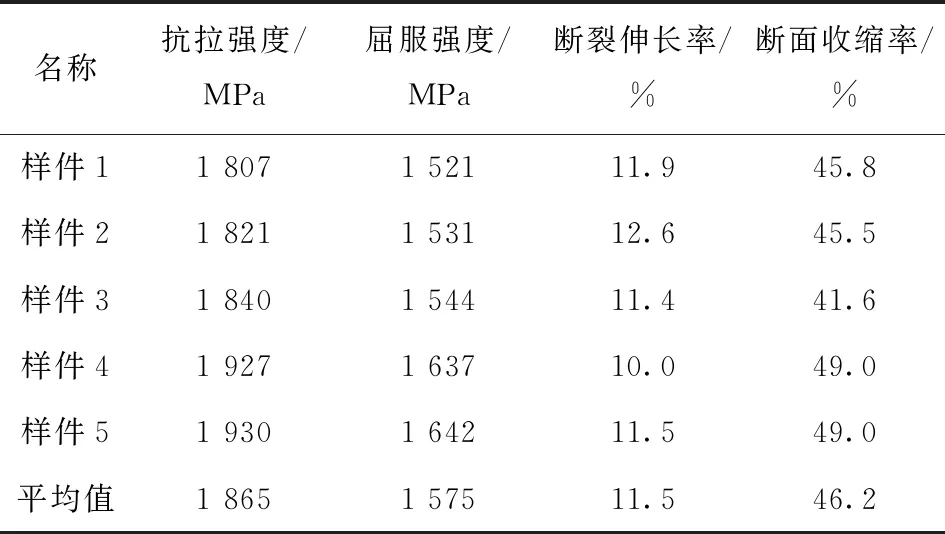
表1 主轴材料力学性能测试结果

表2 循环强度系数和循环应变硬化系数

考虑到采用多线性等向强化模型比双线性等向强化模型精度更高，因此，在有限元模型中主轴材料的弹塑性特性采用多线性等向强化模型[15].

2 主轴弹塑性有限元分析

2.1 主轴弹塑性有限元模型

在保证仿真精度的前提下，对初始设计主轴三维模型进行合理简化，包括去除径向润滑油孔和机加中心定位孔，并将中间输入渐开线花键简化为圆柱面.

基于ANSYS Workbench建立简化后传动主轴的弹塑性有限元分析模型.首先，针对中间圆柱面和两侧输出花键的啮合面分别建立3个远程点(remote point)，并采用四面体进行网格划分；随后，在主轴中间圆柱面的远程点(remote point)施加通过样车测试获得的冲击扭矩均值26 220 N·m；采用远程位移(remote displacement)约束主轴左侧和右侧输出渐开线花键远程点的扭转自由度.主轴有限元网格模型及载荷约束条件如图4所示.

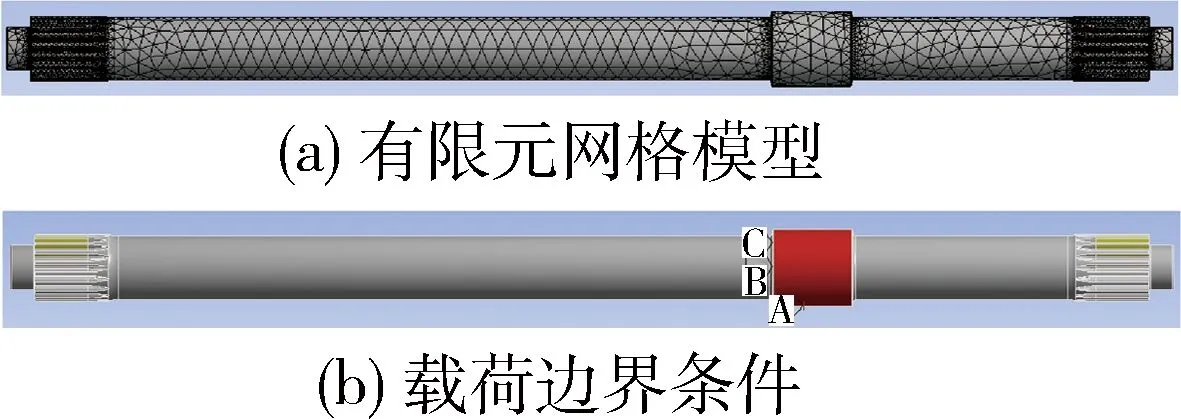
图4 主轴有限元模型及载荷边界条件

2.2 主轴弹塑性有限元分析

图5为起步工况下初始设计的主轴不同位置Mises应力，图中①和②位置分别为主轴左侧花键与退刀槽过渡区齿根和光轴区域，③和④分别为主轴右侧光轴区域和花键与退刀槽过渡区的齿根.主轴左侧位置①和②的Mises应力分别为858 MPa和333 MPa，主轴右侧位置③和④的Mises应力分别为853 MPa和1 598 MPa.经对比分析，起步工况下主轴最大Mises应力发生在右侧，主要原因在于起步工况下主轴两侧花键为固定约束，属于扭转静不定，主轴两侧承受扭矩的比值为两侧扭转刚度之比.另外，由于传动主轴结构布局的限制，主轴两侧为长短不同的非对称结构，当传动主轴两侧的内外径相等，则长度短的一侧(右侧)承担的扭矩大，造成主轴右侧的Mises应力要大于左侧.另外，起步工况下主轴位置④的Mises应力超过了表1中主轴材料的平均屈服强度1 575 MPa，而其余位置的工作应力仍然在弹性范围内.结合主轴右端的局部放大图(图2b)可知，花键啮合时轴向载荷分配不均匀，主轴齿根部位Mises应力沿轴向存在显著差别，同时由于应力集中现象导致主轴右侧最大应力发生在花键与退刀槽过渡区的齿根位置[12-13].对比图5和图1可知，有限元仿真结果与主轴实际裂纹萌生位置一致，验证了有限元模型的合理性.

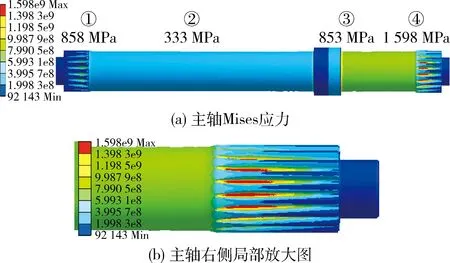
图5 主轴Mises应力仿真结果

2.3 主轴渐开线花键应力集中区域对比分析

采用解析法对主轴渐开线花键应力集中区域进行计算.起步工况下主轴两侧承受的扭矩为

(5)

(6)

式中：T为主轴输入扭矩；Tz和Ty分别为左右侧传递扭矩；Ipz和Ipy分别为左右侧极惯性矩；lz和ly分别为主轴左右侧长度.

获得主轴两侧承受扭矩之后，通过式(7)计算渐开线花键齿根部位的剪应力τs.

(7)

式中：Ti为花键传递扭矩；dr和di分别为花键小径和轴内径；Kt为应力集中系数，采用式(8)计算[13].

(8)

式中：h为轴肩高；r为齿根圆角半径.

主轴Mises应力σs与剪应力τs之间满足式(9).

(9)

主轴两侧花键位置最大Mises应力的计算结果对比如表3所示，表3同时给出了采用GB 17855标准的计算结果.经对比分析可知，采用解析法和GB 17855标准得到主轴左侧花键的Mises应力的计算结果均大于有限元结果，且最大偏差为9.7%.主要原因在于传动主轴右侧花键最大Mises应力已经超过材料的屈服极限并进入塑性状态，应力集中系数较弹性阶段降低[16]，且右侧输出花键的应力集中系数较左侧输出花键降低了32%.

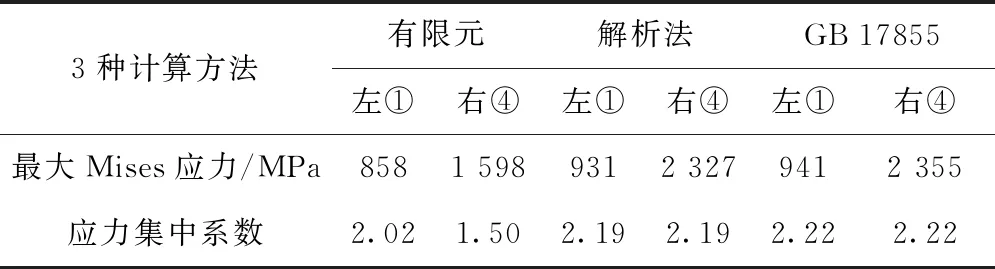
表3 最大Mises应力和最大切应力对比结果

3 主轴结构参数对应力和应变的影响规律

由于传动系统几何边界约束，所以重点改变传动主轴右侧的结构参数.依据2.2节的分析结论，取右侧光轴外径小于花键小径51.6 mm，这样减小了右侧扭转刚度，使得右侧承担扭矩变小，示意图如图6所示，图中R为主轴右侧光轴外径，r为光轴与两侧过渡截面的圆角半径.

图6 主轴改进结构示意图

不同主轴右侧光轴外径和圆角半径下，最大Mises应力仿真结果如表4和图7所示，最大等效应变仿真结果如表5和图8所示.由最大Mises应力仿真结果可以看出：圆角半径r不变，主轴最大Mises应力随光轴外径R的增加整体呈减小的趋势；光轴外径半径R不变，主轴最大Mises应力随圆角半径R的增加整体呈减小的趋势.最大等效应变随光轴外径和圆角半径的变化趋势与最大Mises应力基本一致，不再赘述.当光轴外径R等于48 mm且圆角半径等于10 mm，主轴的最大Mises应力和最大等效应变均达到最优值，分别为1 458 MPa和0.007 29，较初始设计主轴的1 598 MPa和0.011 01，分别降低了8.3%和32.4%.

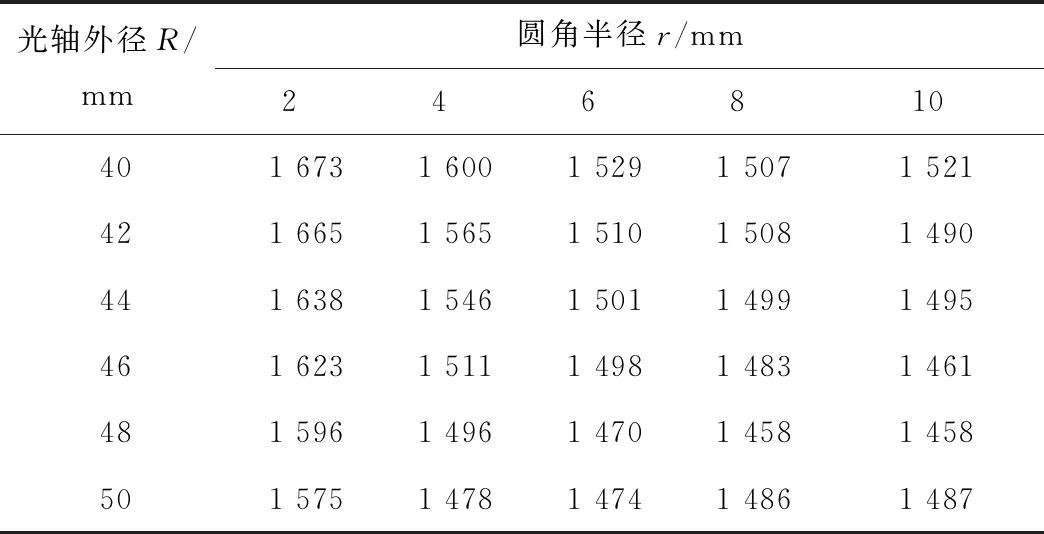
表4 不同外径和圆角半径下主轴最大Mises应力 MPa

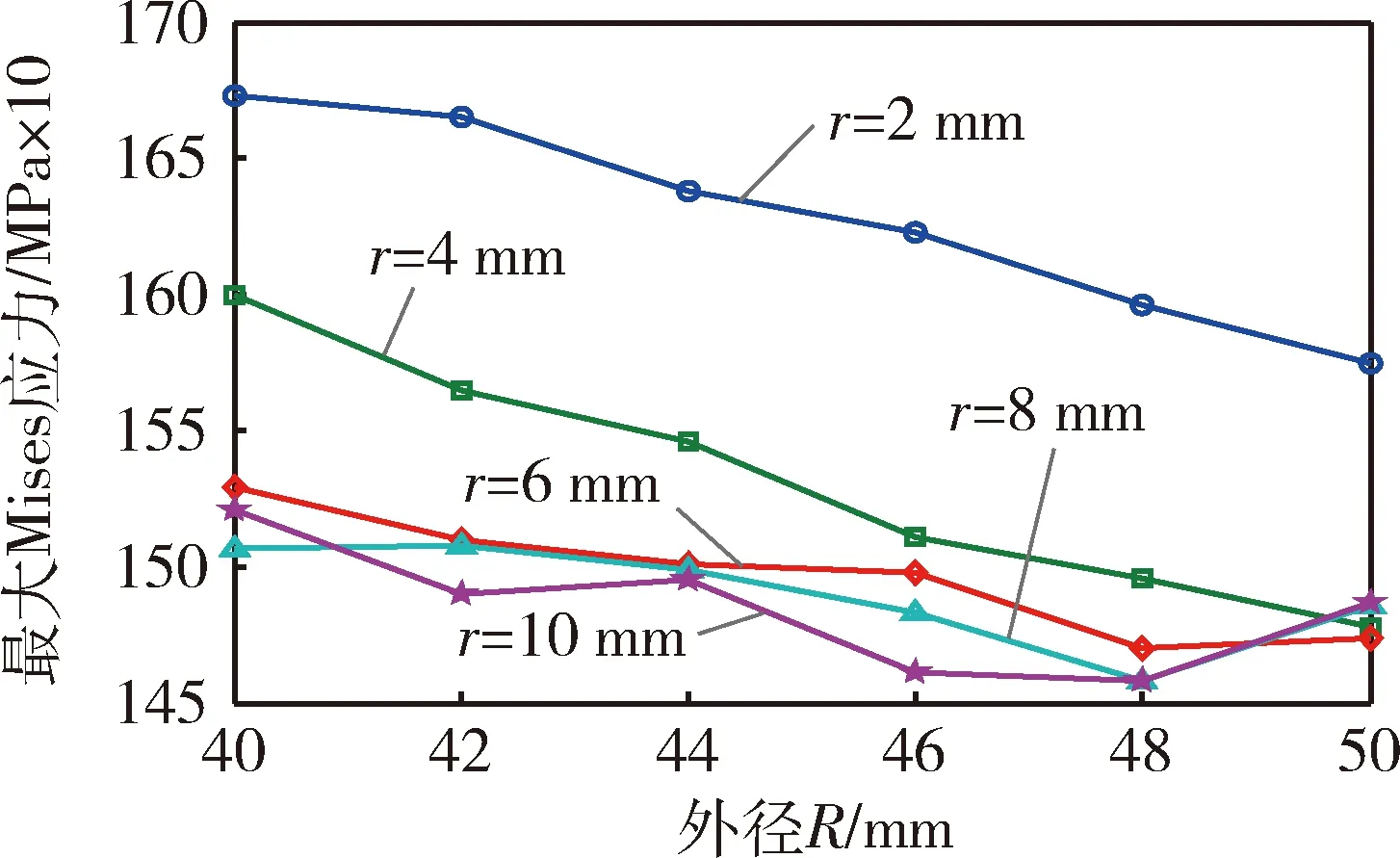
图7 不同外径和圆角半径下主轴最大Mises应力

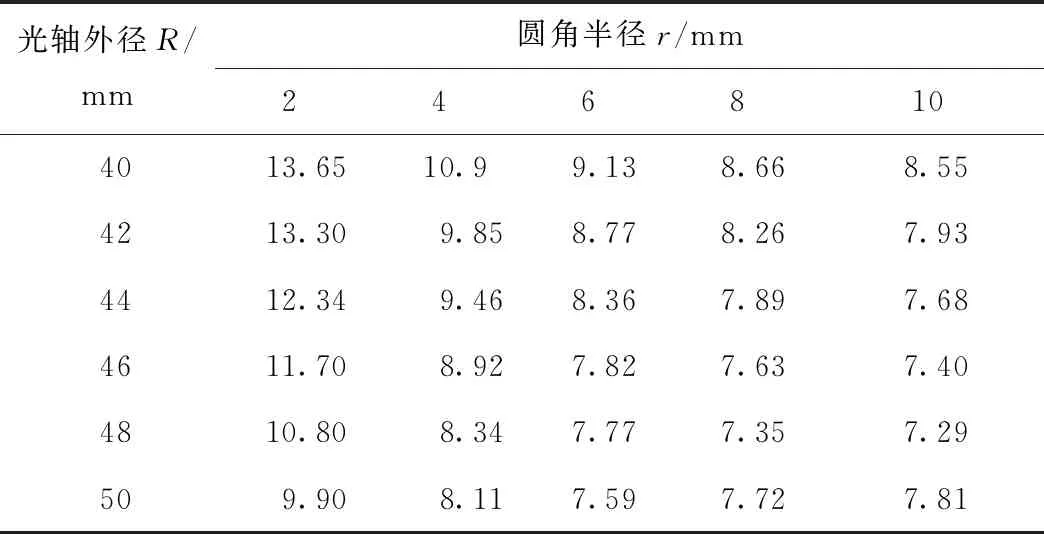
表5 不同外径和圆角半径下主轴最大等效应变 ×10-3

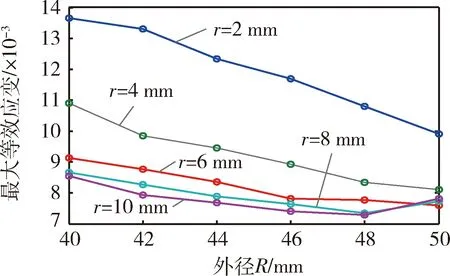
图8 不同外径和圆角半径下主轴最大等效应变

进一步分析右侧光轴外径等于48 mm且圆角半径等于10 mm对应主轴不同位置Mises应力，如图9所示，主轴左侧位置①和②的Mises应力分别为1 264 MPa和764 MPa，主轴右侧位置③和④的Mises应力分别为1 457 MPa和1 436 MPa.与图5中的初始设计主轴相比，位置①、②和③的Mises应力有所提高，而位置④的Mises应力有所降低，主轴两侧更加地接近等强度设计，另外，最大应力位置发生在右侧光轴与花键过渡圆角位置.

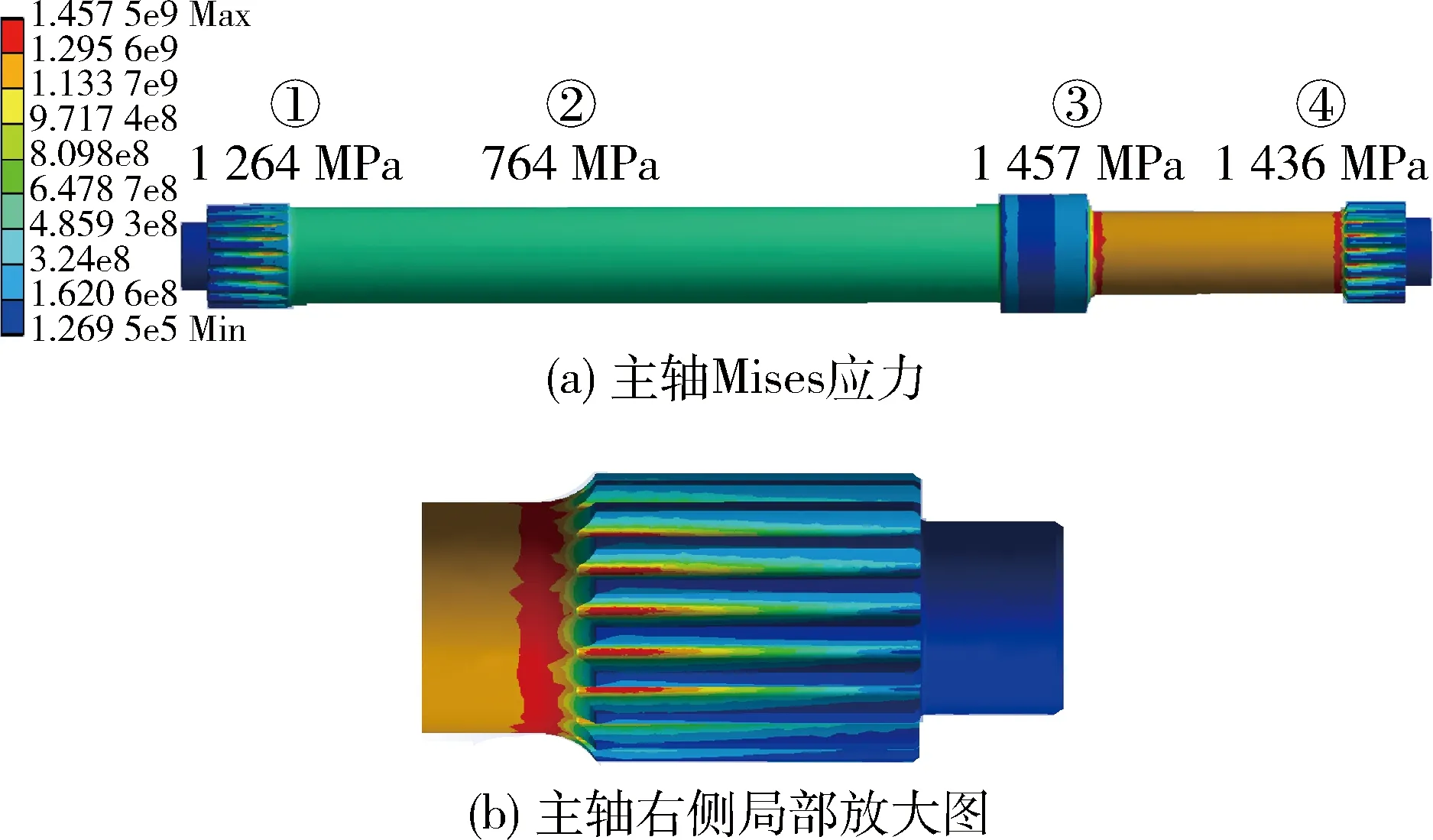
图9 最优结构下主轴最大等效应变

4 主轴低周疲劳寿命预测

履带车辆起步工况下主轴的动态扭矩是比值接近于0的非对称循环载荷，采用基于Mises屈服准则且考虑平均应力效应的Morrow修正模型对主轴的低周疲劳寿命进行预测[17].

(10)

(11)

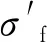
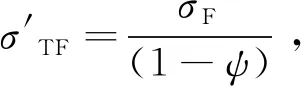
(12)

式中：a/2R=0.88(εTF-εTU)；a为缩颈区最小截面半径；R为缩颈区轮廓线曲率半径;σF为拉伸断裂应力.

首先，将初始设计主轴的最大Mises应力1 598 MPa和等效应变0.011 01，代入低周疲劳寿命预测式(10)，可得预测结果为6 850次.由表4和表5中的应力和应变结果，可得不同主轴右侧光轴外径和圆角半径下主轴的低周疲劳寿命，如表6所示.圆角半径r不变，主轴低周疲劳寿命随光轴外径R的增加整体呈增加的趋势；光轴外径R不变，主轴周疲劳寿命随圆角半径R的增加整体呈增加的趋势.当主轴右侧光轴外径R等于48 mm且圆角半径等于10 mm时，主轴的低周疲劳寿命为 37 779次，较初始设计主轴的低周疲劳寿命6 850次提高了5.5倍.

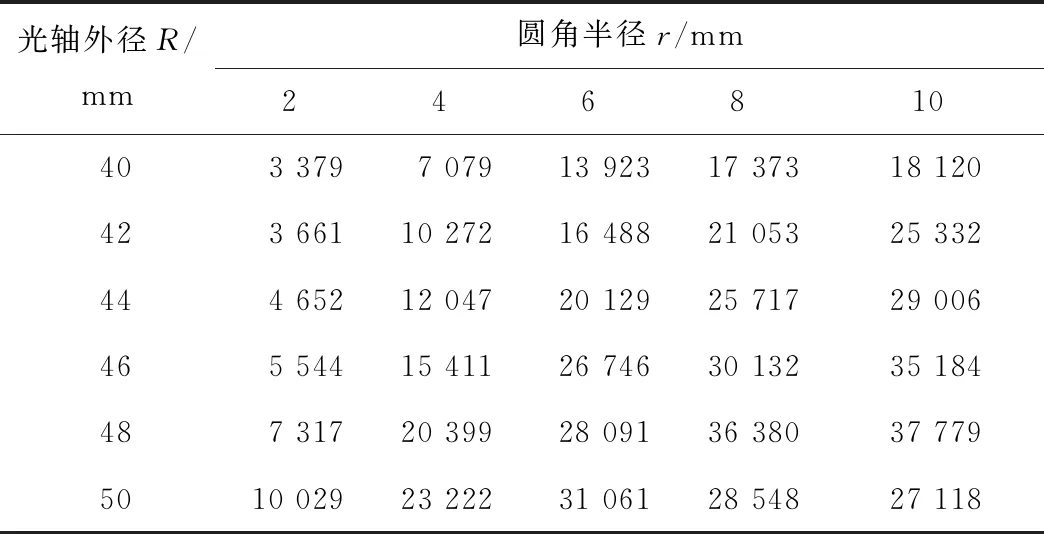
表6 不同外径和圆角半径下主轴疲劳寿命 次

5 结 论

针对履带车辆传动系统主轴低周疲劳失效的问题，获得了主轴材料的弹塑性特性曲线；建立了主轴的弹塑性有限元模型，并与解析计算法和国标进行对比分析；研究了不同结构参数对Mises应力、等效应变的影响规律，基于低周疲劳预测模型获得了主轴的疲劳寿命，主要结论如下：

1)起步工况下传动主轴的最大Mises应力和应变发生在主轴右侧输出花键与退刀槽过渡区的齿根位置，与主轴实际裂纹萌生位置一致，且超过了主轴材料的平均屈服强度；

2)随着右侧光轴外径和过渡圆角的增加，主轴的最大Mises应力和最大等效应变整体上呈现减小的趋势，当右侧光轴外径等于48 mm且圆角半径为10 mm时，最大Mises应力和等效应变达到最小，较初始设计主轴分别降低了8.3%和32.4%；

3)初始设计传动主轴的低周疲劳寿命预测结果为6 850次，最优设计主轴的低周疲劳寿命预测结果为37 779次，较初始设计主轴提高了5.5倍.