四轮独立转向电气式同步控制方案仿真
2021-04-01刘鸿健李春明王东亮
刘鸿健, 李春明, 王东亮
(中国北方车辆研究所,北京100072)
独立转向具有转弯半径小,能快速实现原地、蟹行等多种灵活转向形式的优势,可以满足轮式无人车辆在复杂道路环境下的转向需求.但在转向过程中由于转向角度或转向速度不同步而出现轮胎拖拽的问题,导致无法按照预定轨迹行驶,影响车辆的操纵稳定性[1].本研究针对四轮独立转向无人车辆,如何保持各独立转向轮运动同步的问题,设计了电气式同步控制方案,并建立Simulink模型进行仿真分析.
1 同步控制方案
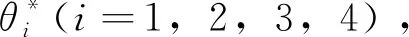
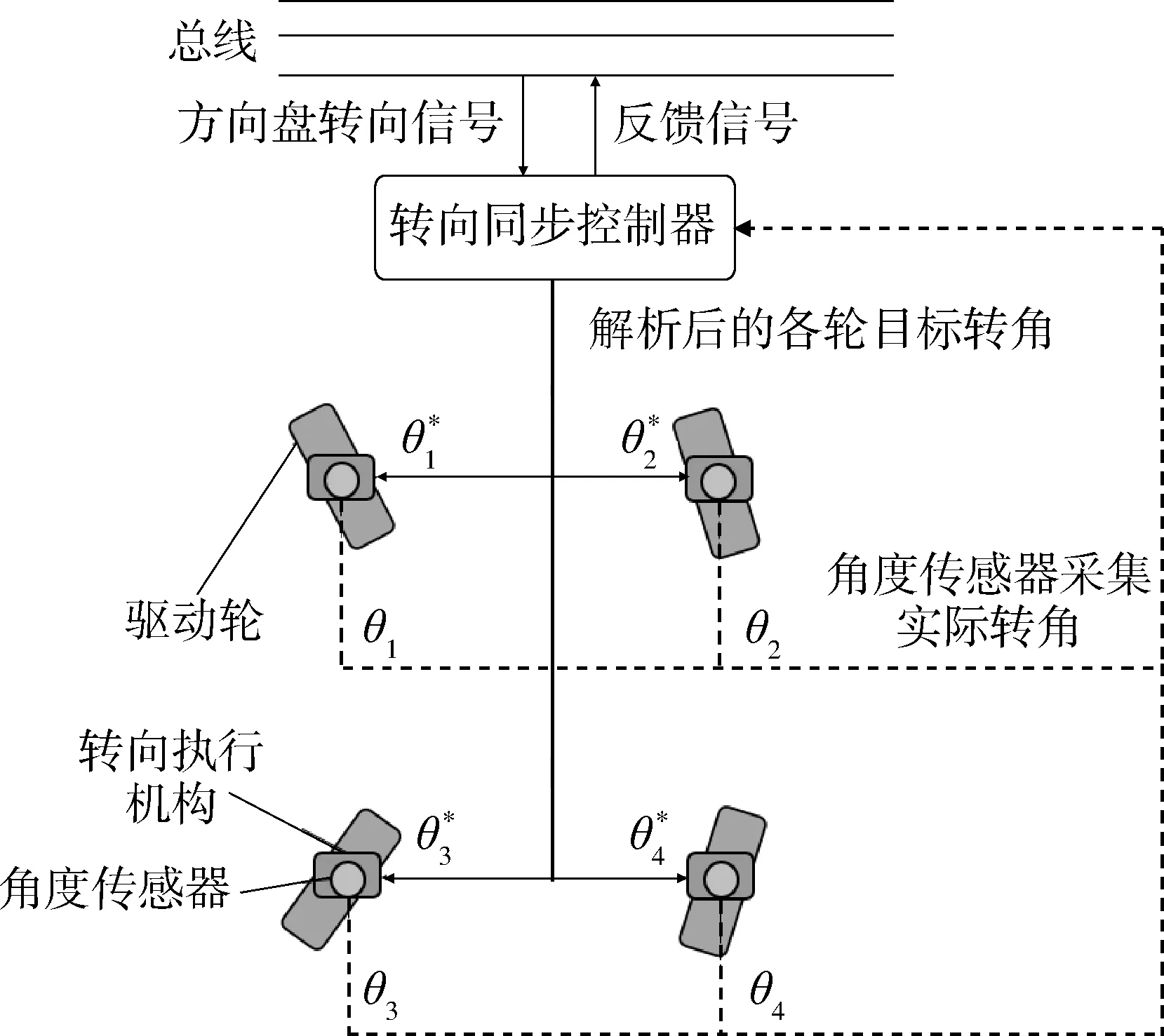
图1 四轮独立转向系统同步控制方案原理图
1.1 转角关系解析
四轮独立转向的几何示意图如图2所示.图中,a、b分别为四轮独立转向车辆的轮距和轴距,G为车辆的质心(假设质心在车体中心),R为质心的转向半径,θ1、θ2、θ3、θ4分别为车辆左前轮、右前轮、左后轮、右后轮的理想转角.
根据阿克曼转向原理,结合图2可得四轮独立转向车辆的内外轮转角关系:
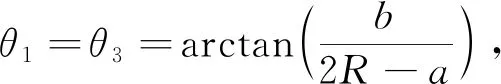
(1)

(2)
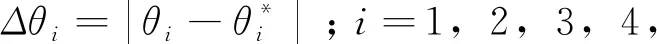
车辆进行独立转向时,由比例调节系数μi可确定各轮转向执行机构的输出转速ωi.ωi应满足同步运动的条件为
ω1∶ω2∶ω3∶ω4=μ1∶μ2∶μ3∶μ4.
(3)
1.2 转速与力矩关系分析
机械式同步控制中,各从动轴与主轴通过机械结构连接,主轴与动力元件连接,各从动轴的扭矩由主轴所分配,并保持严格的同步运动.电气式同步控制借用机械式同步控制的方法,通过设定一根虚拟的主轴来分配力矩并协调各从动轴的运动关系[2].
四轮独立转向电气式同步控制方案结构简图如图3所示.四个独立转向轮为4根从运动轴,虚拟主轴的参考转速为方向盘转速.
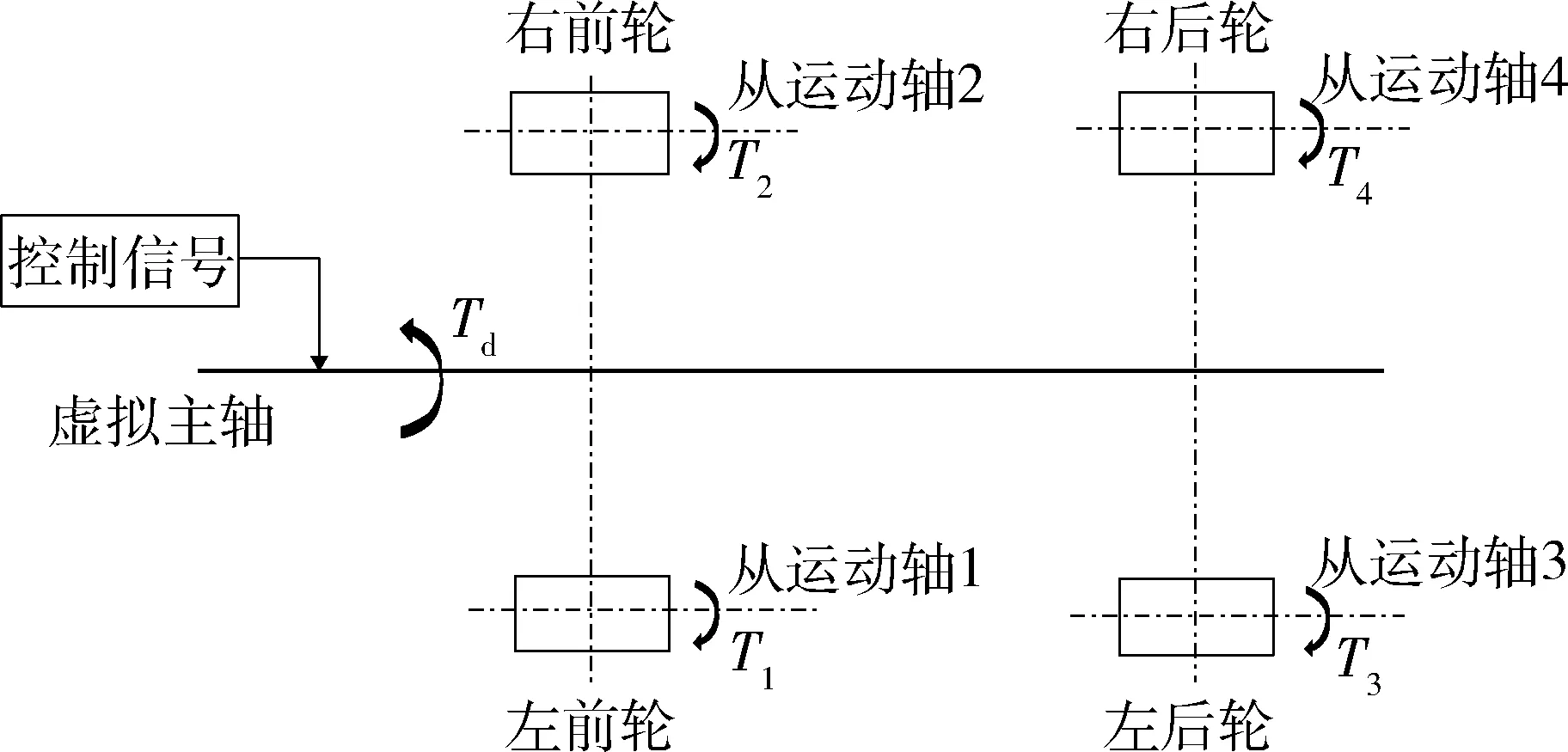
图3 电气式同步控制结构简图
要实现4个独立转向轮的比例同步运动,根据刚体定轴转动定律,需使虚拟主轴驱动力矩与各从运动轴(即转向执行机构)的反馈力矩之和的差值,满足关系式(4)[3].
(4)
式中:Td为虚拟主轴的驱动力矩;Jm为虚拟主轴的转动惯量;ωm为虚拟主轴输出的转速;Ti(i=1,2,3,4)为从运动轴的反馈力矩.
虚拟主轴的驱动力矩Td可用式(5)表述.
(5)
式中:ω*为虚拟主轴的参考转速;bm和Km分别为虚拟主轴的阻尼系数与虚拟主轴的刚度系数;ωm为虚拟主轴的输出转速.
从运动轴的反馈力矩为
(6)
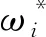
(7)
ωi与Ti的函数关系由转向执行机构的特性,即转向电机的转速-力矩外特性及减速机构传动比确定.结合式(4)~式(7),当各从运动轴的输出转速ωi满足式(3)的比例关系时,各从运动轴达到同步状态.
2 仿真分析
建立虚拟主轴的四轮独立转向系统同步控制Simulink仿真模型如图4所示.
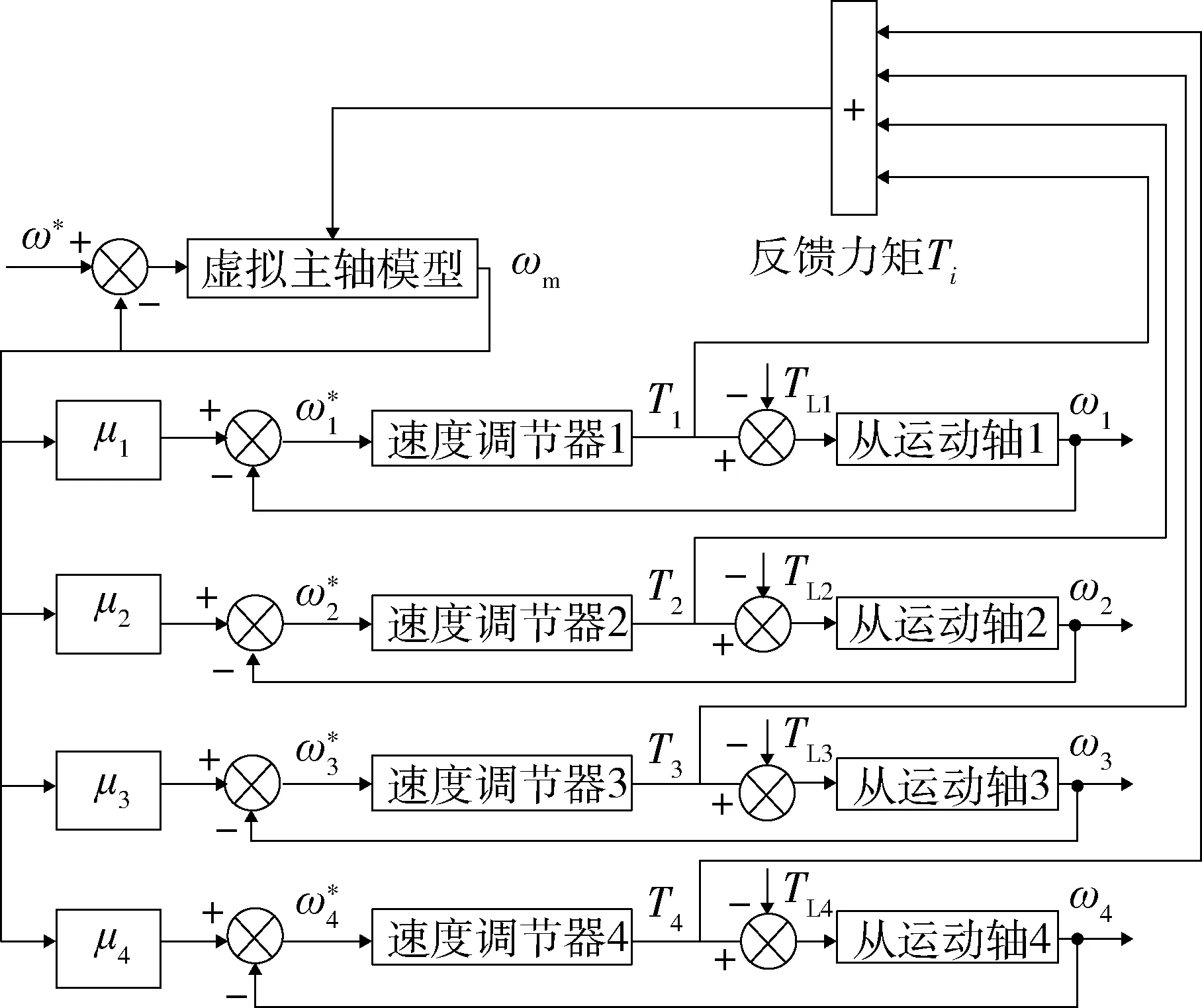
图4 基于虚拟主轴的四轮独立转向系统同步控制仿真模型
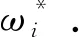
为充分验证该模型的同步控制效果,仿真时选取方向盘输入转角为270°时的初始转向时刻.此时,对应虚拟主轴的参考转速为ω*=90 °/s,各轮实际转角和目标转角的偏差值最大,其比值为
Δθ1∶Δθ2∶Δθ3∶Δθ4=30∶24∶27∶21.
根据式(2)、式(3)可求出各从运动轴保持同步时应满足的输出转速的比例关系为:
ω1∶ω2∶ω3∶ω4=μ1∶μ2∶μ3∶μ4=1∶0.8∶0.9∶0.7
.
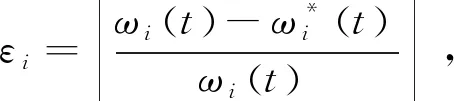
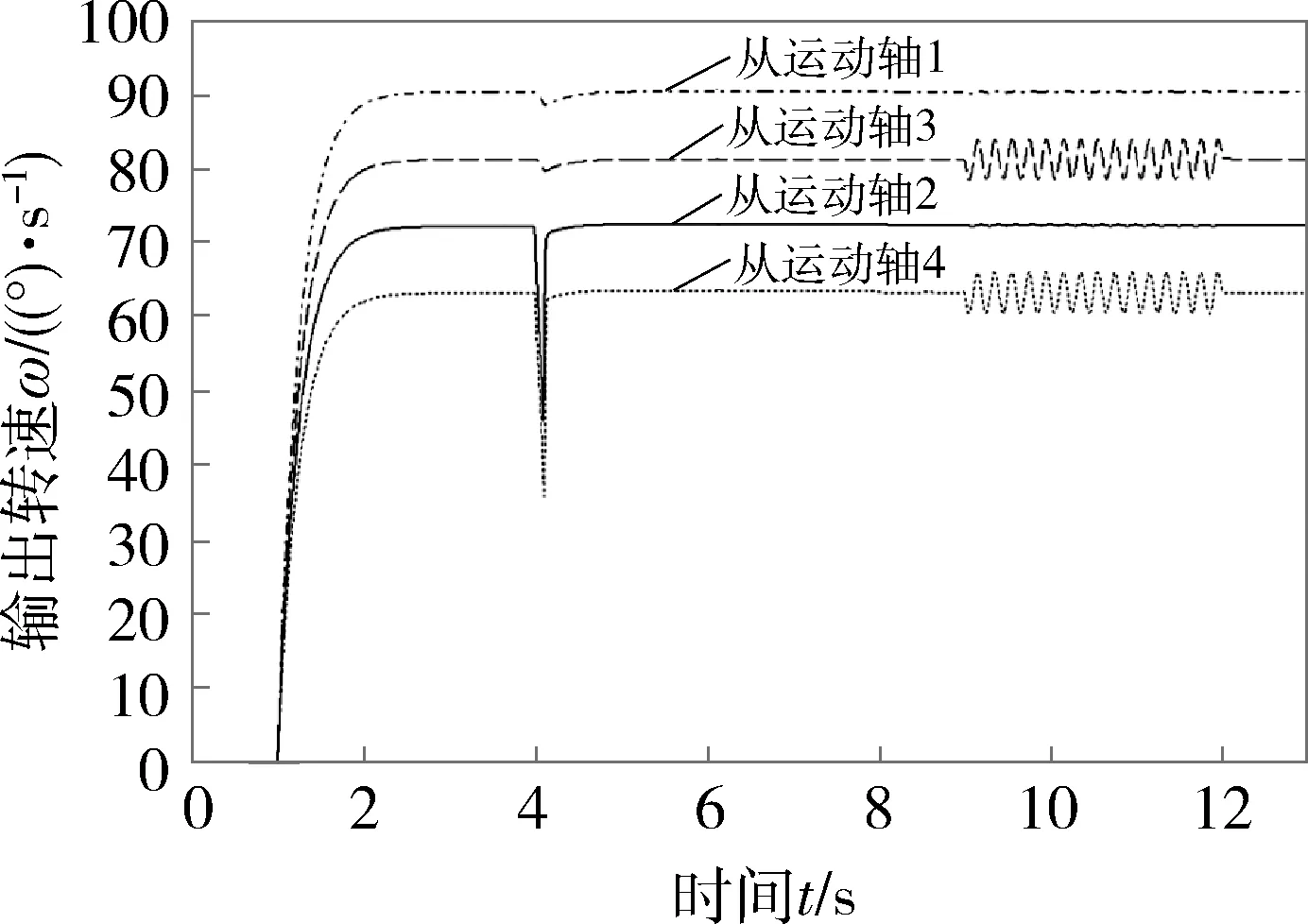
图5 从运动轴的输出转速-时间曲线
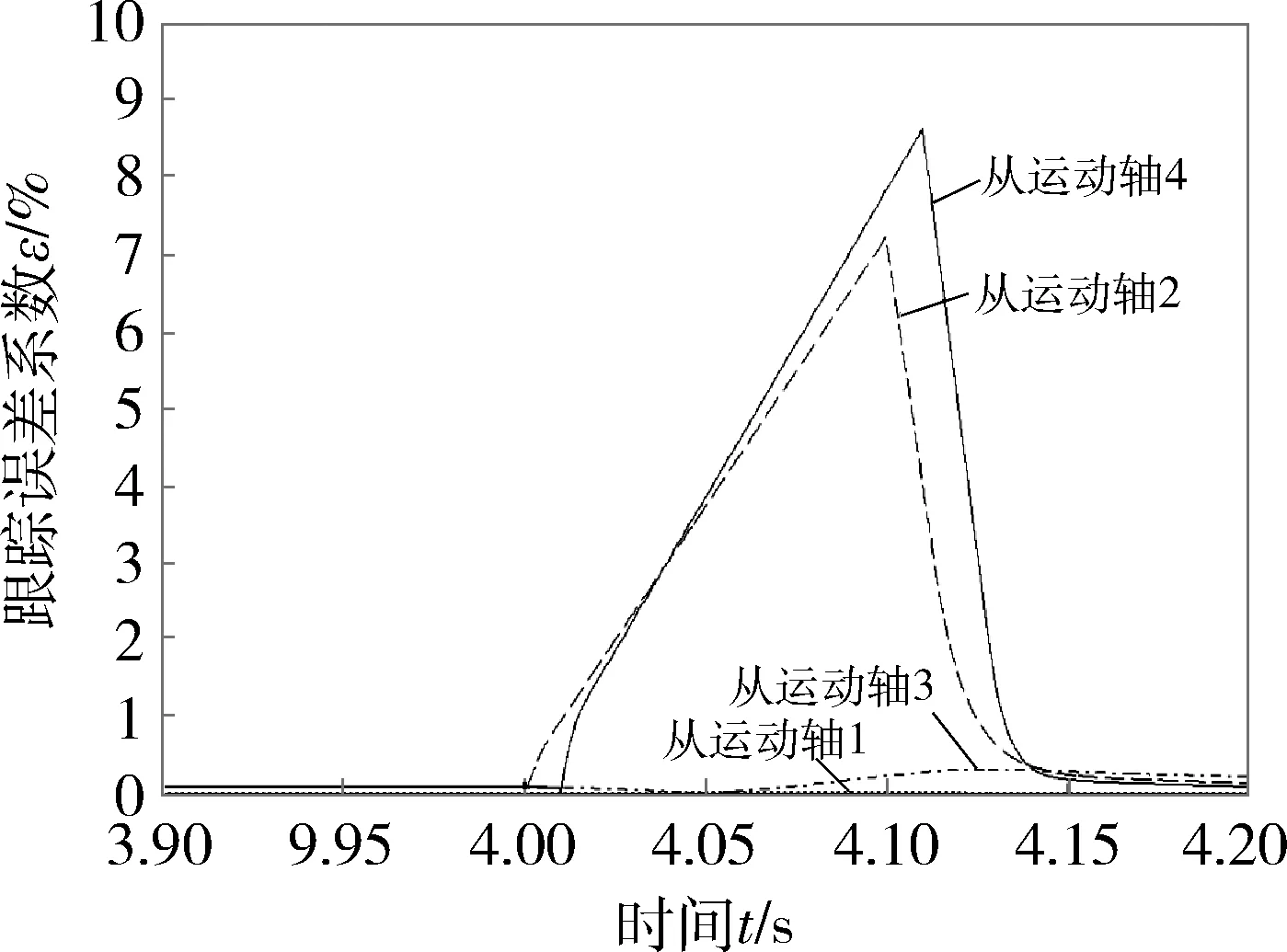
图6 脉冲扰动下4根从运动轴输出转速的跟踪误差系数曲线
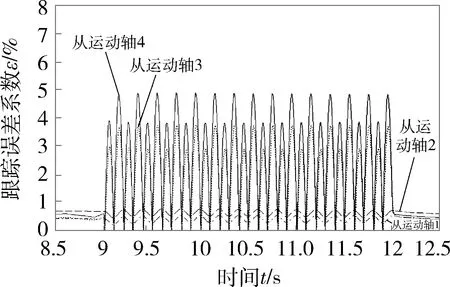
图7 正弦信号扰动下4根从运动轴输出转速的跟踪误差系数曲线
由图5~图7可知:在未受到扰动的情况下,各从运动轴均能快速稳定地达到相应的目标输出转速.在第4 s时给从运动轴2和从运动轴4施加一个等值脉冲扰动,其输出转速的跟踪误差系数能在瞬间(0.15 s)趋于0,而未受主动干扰的运动轴(第1、3轴)几乎不受影响.在第9 s时给从运动轴3和从运动轴4施加一个时长为3 s的等幅正弦扰动,其输出转速的波动幅值为4 °/s,跟踪误差系数小于6%,而其他未受干扰的运动轴输出转速的跟踪误差系数波动极小.结果表明,该电气式同步控制方案,在受到多种外部扰动的情况下,依然具有较好的抗干扰能力和自适应收敛性.
3 结 论
针对四轮独立转向无人车辆的转向同步控制问题,设计了四轮独立转向电气式同步控制方案,并建立Simulink模型进行仿真分析.结论如下:
1)当转向轮在行驶中受到脉冲干扰时,其转向执行机构输出转速虽然会出现较大起伏,但能在瞬间收敛并趋于稳定,而其他未受干扰转向轮的运动几乎不受影响;
2)当转向轮行驶在一段起伏不平的路面下,即受到正弦信号的干扰时,其转向执行机构输出转速的波动副值为4 °/s,跟踪误差系数小于6%.
综上所述,该电气式同步控制方案具有较好的抗干扰性和同步稳定性,能满足轮式无人车辆在复杂道路环境下进行独立转向的同步控制需求.
