缓堵作用下公路突发事件时空影响范围模型

徐 鹏，张 婷

(河海大学 土木与交通学院，江苏 南京 210098)

公路网作为我国交通运输系统中的重要分支，其承担着城市间互相协作和发挥城市经济辐射作用的重任。因此，对区域公路网突发事件影响范围进行分析和研究，在理论层面和现实层面都具有重大意义。与城市道路相比，公路网的交通流在时间上的变化不同，没有明显的早晚高峰；公路网交通流大小和交叉口密集度介于城市道路和高速公路之间，常见车辆主要是机动车，少有非机动车混行，可以从交通波理论角度构建适合于公路网的拥堵扩散分析模型。公路突发事件发生后，上游会及时采取拥堵信息发布等限速措施缓解道路拥堵。突发事件影响范围受上游缓堵作用干预，掌握突发事件本身产生的集结波、道路清障产生的消散波以及上游缓堵措施产生的缓堵波之间相互作用下公路受突发事件的影响情况，对后续交通应急组织的有效实施至关重要。

突发事件影响范围一直是国内外学者重要研究的内容。大量学者从不同的理论出发，研究出各种不同适用范围的模型。陈绍宽等[1]将时间维度引入到传统的Moran’s I指数中，分析了城市道路交通状态的时空变化规律。CHIEN等[2]通过交通波理论，分析了不同交通场景的道路事件的延误情况，并基于此建立了一种计算突发事件总延误时间的模型，但是计算得出的总延误与交通仿真软件仿真结果相比存在很大误差。YANG等[3]将皮尔逊相关系数应用到时间自相关分析与交通时空相关性分析，研究了能对道路状态进行较好预测并能及时应对道路突发事件的模型。王云鹏[4]通过分析高速公路发生事件后上游交通流的排队和消散过程，建立了多车道封锁情况下高速公路的事件影响时空范围模型，但是该模型没有考虑实际道路情况中上游由于拥堵信息发布产生的交通波对拥堵的缓解反应，模型计算的事件总影响时间与实际相比会偏大。王建军[5]基于流体力学车流理论，研究了在干预措施作用下的突发事件对道路交通状态的改变过程，并提出干预措施作用的3种情况的车流波波速模型以及干预措施解除后的车速变化模型。金书鑫[6]将拓扑关系理论应用到区域高速路网交通事故影响区划分中，按道路节点重要度对事故处理先后顺序进行划分从而达到提高事故处理效率的目的。何雅琴[7]借用水波原理提出了交通影响系数的概念，设计了一个基于时间和距离的交通影响系数模型，并计算出突发事件综合影响程度。HOJATI等[8]研究了道路上各种因素作用下交通事故影响的持续时间模型，为缩短事故影响时间的措施提供依据。李扬等[9]对新增车辆的通行拥堵进行预测，使用K-Medoids聚类算法将交通流运行状态划分为顺畅、阻滞、拥堵三类，引入交通流特征参数构建累积Logistic回归模型量化新增车辆对路段运行状态的影响，最后基于支持向量回归机预测新增车辆通行时间。

目前国内外面向公路网模型的研究较少，忽略了公路网的特点在突发事件引起的交通拥堵传播范围中的影响，对公路网的事件拥堵特征研究不具备良好参考性，故本文设计了一种针对公路网突发事件的时空影响范围模型。

1 基于交通波理论的双车道拥堵消散过程

当区域公路网发生突发事件时，事件发生点处的交通通行能力发生骤减而形成一个虚拟瓶颈；当事件发生点占用车道导致交通供给能力下降以至不能满足交通需求，在采取疏导措施之前，拥堵向事件所在路段上游蔓延并扩大到周围路网[10]。由于公路网没有明显的高峰时间段，故可以将交通车流看作匀速的，交通波沿道路匀速移动。从空间上看，道路出现拥堵后，突发事件影响线会随着车辆排队的增加向上游运动。交通拥堵扩散示意如图1所示。由图1可见，当拥堵的集结波从瓶颈处向上游扩散时，更多路段的通行能力和速度也随着事件影响线的运动而下降。

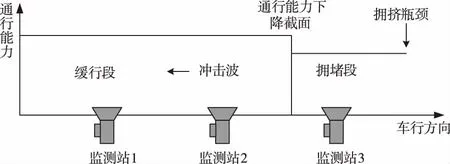
图1 交通拥堵扩散示意图Fig.1 Schematic diagram of traffic congestion dispersion

按交通波理论，当公路上车流因突发事件发生而引起交通密度变化时，会在车流中产生密度不同的两部分界面的波的传播[11]。设密度不同的两部分界面沿空间传播的波速为U(K1，K2)，则波速的一般表达式为

(1)

式中：Q1，Q2分别为上游交通量、下游交通量，veh/h；K1，K2分别为上游交通密度、下游交通密度，veh/km。

拥堵传播一段时间后，由于拥堵信息传播，上游交通分流的作用或者车速控制的作用，从分流点形成一个缓堵波并向上游传播，会对事件影响线的移动产生影响。采取事件点清障措施后，道路通行能力恢复，消散波开始向上游传播，同时事件影响线将向下游移动。因此，本文研究在缓堵波的干涉下，突发事件产生的集结波和道路清障产生的消散波所确定的公路突发事件时空影响范围。

本文以公路为研究对象，以双车道发生突发事件为例，考虑到事件点车道清障需要分次处理，如果在整个双车道路段以及时间组成的时空区域内研究交通波的全程，则事件影响的空间和时间范围可以分为3个时区：(1)事件发生后，两条车道都被封锁，事件发生点上游形成拥堵并逐渐蔓延；(2)其中一条车道清障完成，该车道交通流逐渐恢复；(3)另一条车道清障完成，事件点断面逐渐恢复正常通行能力[12]。

没有缓堵波作用时的双车道拥堵影响过程如图2所示。由图2可以看出：事件发生时刻t=0，发生位置的横断面L=0(L为事故影响线距离)，此时双车道都被封锁，产生从事件点出发向上游传播的波速为W12的集结波；在t1时刻，两条道路中任一条完成清障工作，其产生从事件点出发向上游传播的消散波，波速为W23；两者在t2时刻汇集产生波速为W13的新消散波，此后在两条道路上只有波速为W13的交通波；在t3时刻，另一条道路完成清障工作，其产生从事件点出发向上游传播的消散波，波速为W34；在t4时刻，波速为W34的消散波与波速为W13的交通波汇集成新的消散波，波速为W14；直到tmax时刻，道路上的交通状态完全恢复，事件影响得以消除[9]。

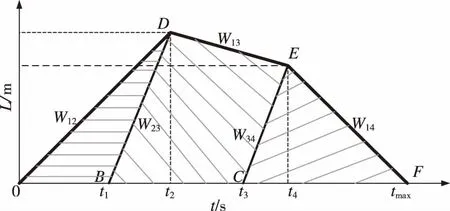
图2 无缓堵波作用时的拥堵扩散过程Fig.2 Congestion diffusion process without action of easing congestion wave

当事件发生后的某时刻，在上游某一点由于拥堵信息的发布使得车流量减少而产生一个向上游传播的缓堵波时，若该缓堵波和以上的集结波或消散波相遇，则会对上述的拥堵影响过程产生一种良性的干扰，加速拥堵消散过程[13]。缓堵波与其他交通波相遇的情况可以分为3种时区，分别是与W12、W13、W14相遇，这3种情况对解除事件影响的过程有所差异。

2 控制波干涉作用下时空影响范围模型

2.1 缓堵波在时区1与事件影响线相遇

假设在突发事件发生前，车道路段上的交通流是均匀的，交通状态描述为(V0、K0、Q0)，表示为初始状态，其中：V0为初始车流速度；K0为初始车流密度；Q0为初始交通流量[14]。缓堵波和集结波在事发路段的传播过程如图3所示。ND段和OD段分别表示缓堵波和集结波在相遇之前的运动过程，DE段表示两波相遇之后形成新的交通波的传播过程[9]。

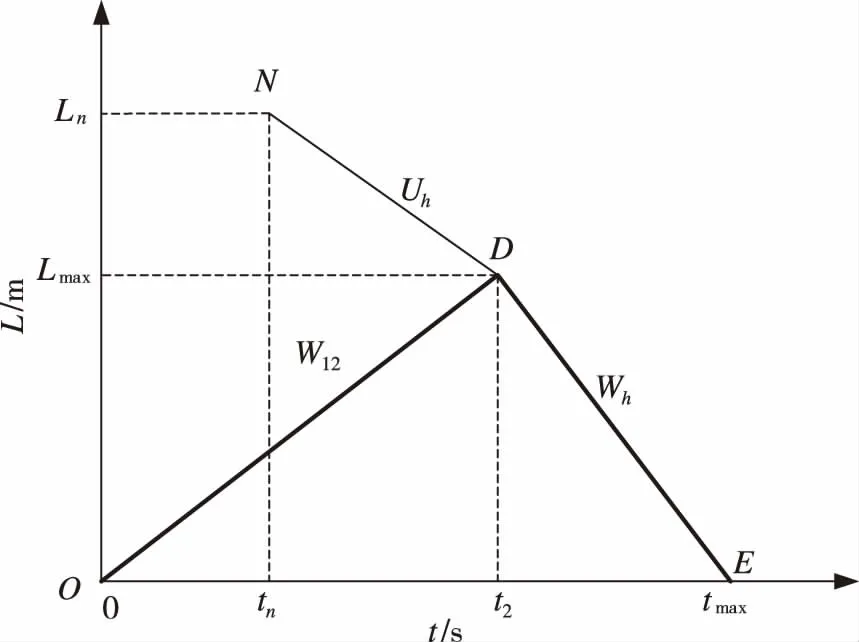
图3 缓堵波作用于时区1的拥堵扩散过程Fig.3 The effect of easing congestion wave on the congestion diffusion process in time zone one

在tn时刻，上游距离事发点Ln处产生一缓堵波，此时Ln处下游的交通状态为(Vn、Kn、Qn)，则该缓堵波的波速Uh为

(2)

设该缓堵波向下游运动与集结波相遇的时刻为t2，则由方程

Uh×(t2-tn)+W12×t2=Ln

(3)

得

(4)

两波相遇点距离事件发生点的距离为Lmax(即为事件最长影响距离)，之后两者形成波速为Wh的新消散波，其到达事件点的时刻为tmax(即为事件最长影响时间)，则

Lmax=W12×t2，

(5)

(6)

由以上可得事件的时空影响域为

(7)

2.2 缓堵波在时区2与事件影响线相遇

突发事件发生前交通状态为(V0、K0、Q0)，表示为初始状态，其中：V0为初始车流速度；K0为初始车流密度；Q0为初始交通流量。缓堵波和交通波在事发路段的传播过程如图4所示。

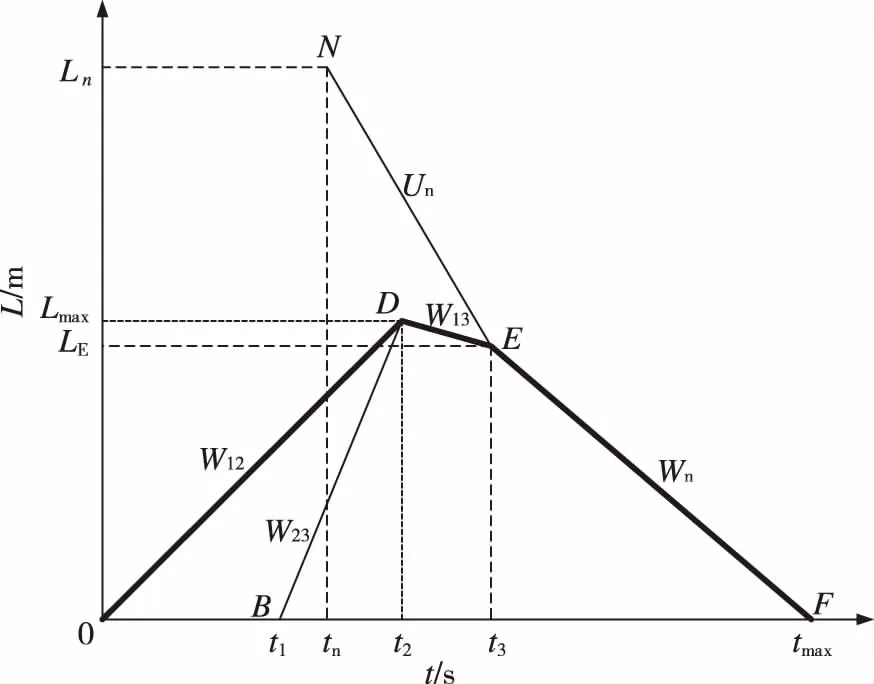
图4 缓堵波作用于时区2的拥堵扩散过程Fig.4 The effect of easing congestion wave on the congestion diffusion process in time zone two

在t1时刻，双车道其中一条车道完成清障工作；在t2时刻，波速为W12和W23的两波相遇形成波速为W13的新交通波，并在t2时刻达到最大拥堵长度Lmax。

(8)

(9)

在tn时刻，上游距离事发点Ln处产生一缓堵波，波速为Un。NE段表示该缓堵波与波速为W13的交通波在相遇之前的运动过程，EF段表示该缓堵波与波速为W13的交通波在t3时刻相遇之后形成的波速为Wn的新交通波的传播过程。由方程

Un×(t3-tn)+[Lmax-W13×(t3-t2)]=Ln

(10)

得

(11)

到tmax时刻，波速为Wn的交通波传播到达事件发生点结束，tmax即为事件最长影响时间。

(12)

由以上可得事件的时空影响域为

(13)

2.3 缓堵波在时区3与事件影响线相遇

突发事件发生前交通状态为(V0、K0、Q0)，表示为初始状态，其中：V0为初始车流速度；K0为初始车流密度；Q0为初始交通流量。缓堵波和交通波在事发路段的传播过程如图5所示。

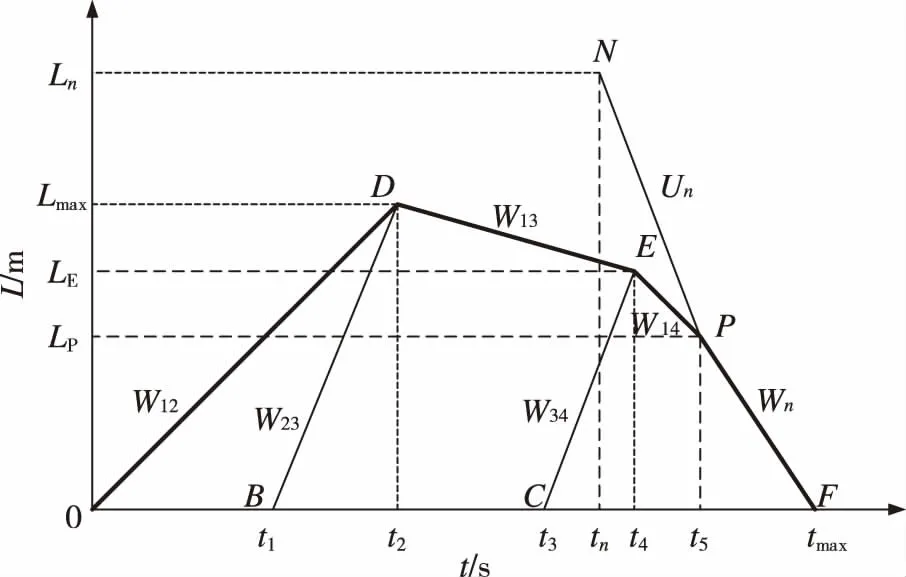
图5 缓堵波作用于时区3的拥堵扩散过程Fig.5 The effect of easing congestion wave on the congestion diffusion process in time zone three

在t1时刻，双车道其中一条车道完成清障工作；在t2时刻，波速为W12和W23的两波相遇形成波速为W13的新交通波，并在t2时刻达到最大拥堵长度Lmax；在t3时刻，另外一条车道完成清障工作；在t4时刻，波速为W13和W34的两波相遇形成波速为W14新交通波。t2和t3算法与之前相同，本节不再重复计算。由方程

Lmax=W34×(t4-t3) +W13×(t4-t2)

(14)

得

(15)

在tn时刻，上游距离事发点Ln处产生一波速为Un的缓堵波。EP段表示该缓堵波和波速为W14的交通波相遇之前的运动过程，PF段表示该缓堵波和波速为W14交通波在t5时刻相遇之后形成的波速为Wn的新交通波的传播过程。由方程

Ln-Lmax=Un×(t5-tn)-W13×(tn-t2)-W34×(t5-t4)

(16)

得

(17)

最长影响时间tmax为

(18)

由以上可得出该情况下事件的时空影响域为

(19)

3 实例分析

本文以南京市六合县龙池至安徽省天长县的区域公路网中某双车道一级公路为例。已知道路通行能力为1 200 pcu/h，设计时速为50 km/h。在t=0时刻，在路段某截面发生一起突发事件导致两条车道都被封锁无法通行，堵塞车流密度为55 pcu/km，事发后车流量为1 000 pcu/h，车流密度为45.8 pcu/km，事件发生后t=0.4 h其中一条车道清障完成，t=0.8 h另一条车道清障也完成。用交通流量-密度图来计算交通波波速，将流量密度图的抛物线函数简化为直线函数[15]，曲线图上两点之间连线的斜率的绝对值为交通波波速，如图6所示。图6中，点A表示的交通状态是事件发生前，点B表示的交通状态是事件发生后双车道都被封锁后，点C表示的交通状态是一条车道完成清理后，点D表示的交通状态是两条车道均解除封锁后。

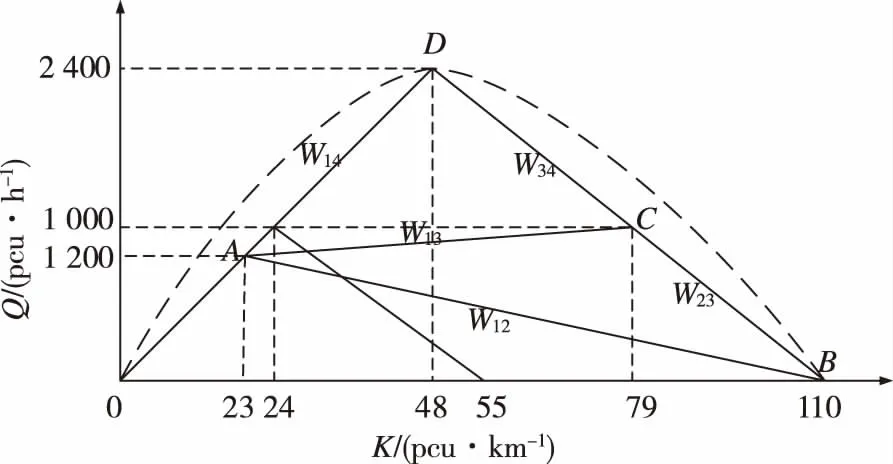
图6 事件发生过程的流量-密度Fig.6 Traffic quantity-density during event occurrence

用(K，Q)表示各点坐标，K的单位为pcu/km，Q的单位为pcu/h。点A为(23，1 000)，点B为(110，0)，点C为(79，1 200)，点D为(48，2 400)。交通波波速计算结果都用绝对值，则W12=13 km/h，W23=39.7 km/h，W13=3.6 km/h，W34=39.7 km/h，W14=50 km/h。缓堵波作用在时区3时，设Ln=10 km，Un=60 km/h，tn=1.0 h，则按2.3节计算得事发截面上游影响范围为

最大影响长度Lmax和最大影响时长tmax分别为

Lmax=7.7 km，

tmax=1.250 h。

4 模型验证

本文使用基于驾驶行为的交通仿真软件vissim模拟验证以上算例计算结果的准确性。案例的参数设置与上述案例相同，整条路段长度设为10 000 m，交通事件发生时间设为1 000 s，事发后1 h内车流量为1 000 pcu/h，车流密度为45.8 pcu/km，事发1小时后事发点上游1 000 m的车流密度开始上升为55 pcu/km。在vissim软件中[16]，将事件发生点的车道封锁和封锁解除的过程用交通信号灯来等效模拟。交通信号灯参数如图7所示。由图7可见：在1 000 s时两条车道都封锁，0.4 h后一条车道解除封锁并恢复通行，再过0.4 h后另一条车道也恢复通行。软件运行结果如图8所示。图8分别描述了“车道全部封锁”“一条车道解除封锁”“车道全部开放”3个阶段的道路拥堵集结消散情况。

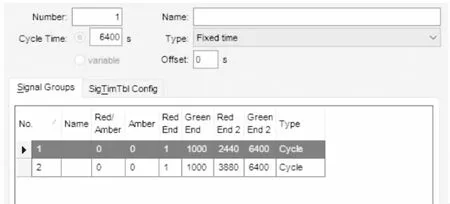
图7 交通信号灯参数Fig.7 Traffic signal parameters

图8 软件运行结果Fig.8 Results of software operation

使用vissim中的数据采集器，得出事件发生后拥堵最大影响长度是7.2 km，拥堵从发生到完全恢复正常交通状态所用时间为1.183 h。公式计算结果和vissim运行结果的对比，见表1。

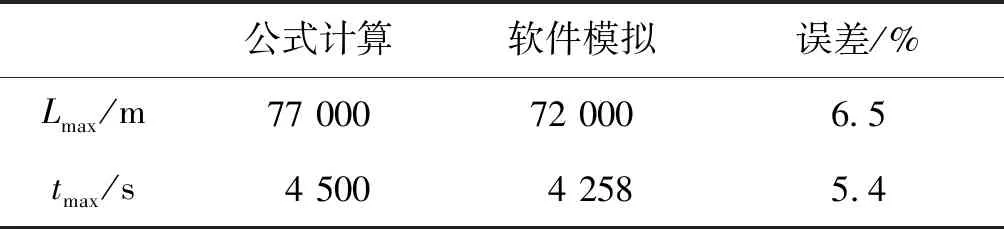
表1 数据对比

将以上模型计算结果与vissim仿真结果进行对比，可得出模型计算的实时拥堵排队长度和排队时间的平均误差在7%以内，说明本文模型能较好地估算公路突发事件的时空影响范围[17]。但由于只是对双车道公路网进行了仿真实验，针对不同车道数的公路网拥堵状况，模型还应优化。

5 结语

从交通波的理论出发，通过分析公路突发事件引起的拥堵传播过程的规律和特点，将拥堵传播过程划分为几个时区。考虑到下游分流和限速措施对不同时区拥堵传播的影响，结合数学分析的方法，计算出了不同时区内公路突发事件的时空影响范围模型。最后经过实际数据计算出了事件最长影响距离和最长影响时间，发现该模型在确定公路事件的处理方法、处理时机以及预测事件的时空影响范围中能得到应用。