含能材料感度评估的空间位阻指数算法和程序设计
2021-04-06刘知涵薛向贵
崔 涛,刘知涵,谢 玮,薛向贵
(1. 上海大学理学院化学系,上海 200444;2. 上海大学材料基因组工程研究院,上海 200444;3. 中国工程物理研究院化工材料研究所,四川 绵阳 621999)
1 引言
含能材料的感度研究在近年愈发受到关注。以实验方式得到含能材料的撞击感度需要合成含能材料大单晶因而比较困难,如何通过非实验的方式比较不同含能材料的撞击感度一直是此领域的研究热点。在过去对含能材料撞击感度的研究中,Menikoff等[1]及Dick 等[2]报道了奥克托今(HMX)的β 相在撞击载荷下的塑性变形与滑移运动直接相关,热力学响应和撞击感度具有明显的各向异性,晶体内滑移面两侧的空间位阻对各向异性的感度起主要作用,且敏感晶面的空间位阻大。 Zyben[3]使用基于ReaxFF 反应力场的分子动力学模拟研究了太安(PETN)单晶在压缩-剪切载荷下的物理化学响应,计算得到的热力学响应和撞击感度的各向异性与撞击实验结果一致。Swell 等[4]报道了HMX 的塑性变形以沿着某些滑移系的位错运动为主。同年An 等[5]使用压缩-剪切反应动力学(compress-and-shear reactive dynamics,CS-RD)模拟研究了奥克托今(RDX)晶体的撞击感度的各向异性,所得计算结果与已有实验具有较高的一致性。但是,由于缺乏合适的力场等原因,苯并氧化呋咱(BTF)和梯恩梯(TNT)等仍未有公开的CS-RD 记录报道,因此使用第一性原理和其他方法研究含能材料撞击感度仍存在较大的发展空间。
除了分子动力学模拟以外,An 等[5]还基于含能材料中分子重叠程度定义了空间位阻指数(Steric Hindrance Index,SHI)。使用SHI 定量评估和预测含能材料撞击感度的优势在于只需晶体结构作为输入,不考虑原子驰豫和化学反应,无须做代价昂贵的分子动力学模拟,因而高效且独立于力场。尽管An等[5]定义了SHI,但受制于自动计算算法及其程序实现的缺乏,仅手动计算了RDX 晶体的(100)/{-110}<110>和(110)/{010}<100>两个滑移系的SHI。本文在An 的研究基础上,开发出具有材料普适性的SHI 自动计算算法,并使用Python3 进行程序实现。用户在程序中仅需输入正交晶系的含能材料的cif 文件,即可计算任意一个滑移系的SHI,相比于涉及力场的CS-RD 计算方法极大的简化了计算过程。
2 设计目标与算法
2.1 空间位阻指数的定义
如图1 所示,含能材料受到某一方向的撞击后,在沿撞击平面(图1 示例中为(110)晶面)一定夹角θ(图1 示例中θ=45°)产生剪切滑移面(也叫剪切带)。通过沿撞击方向等轴缩放晶体来压缩分子。将每个分子中的各个原子视作球体,将压缩后分子中的各个原子完整几何投影至剪切滑移面(图1 示例中为{010}面)的垂直平面上(图1 示例中为底面)。对指定的滑移系建立新的空间直角坐标系并旋转晶胞以处理任意撞击方向和滑移系,将旋转后的晶胞内分子根据质心的x 坐标进行分层,如图2。如果相邻平面上的分子在投影后重叠,则在投影平面上的位置给出一个阴影点,即重叠数加一。将重叠数加权的重叠区域面积相加,相对于投影横截面的比率即被定义为空间位阻指数。空间位阻指数可以绘制二维等值线图,其中重叠区域表示在剪切过程中可能发生空间位阻的区域。

图1 分子在剪切形变过程中的空间位阻示意图Fig.1 Schematic diagram of steric hindrance of molecules during shear deformation
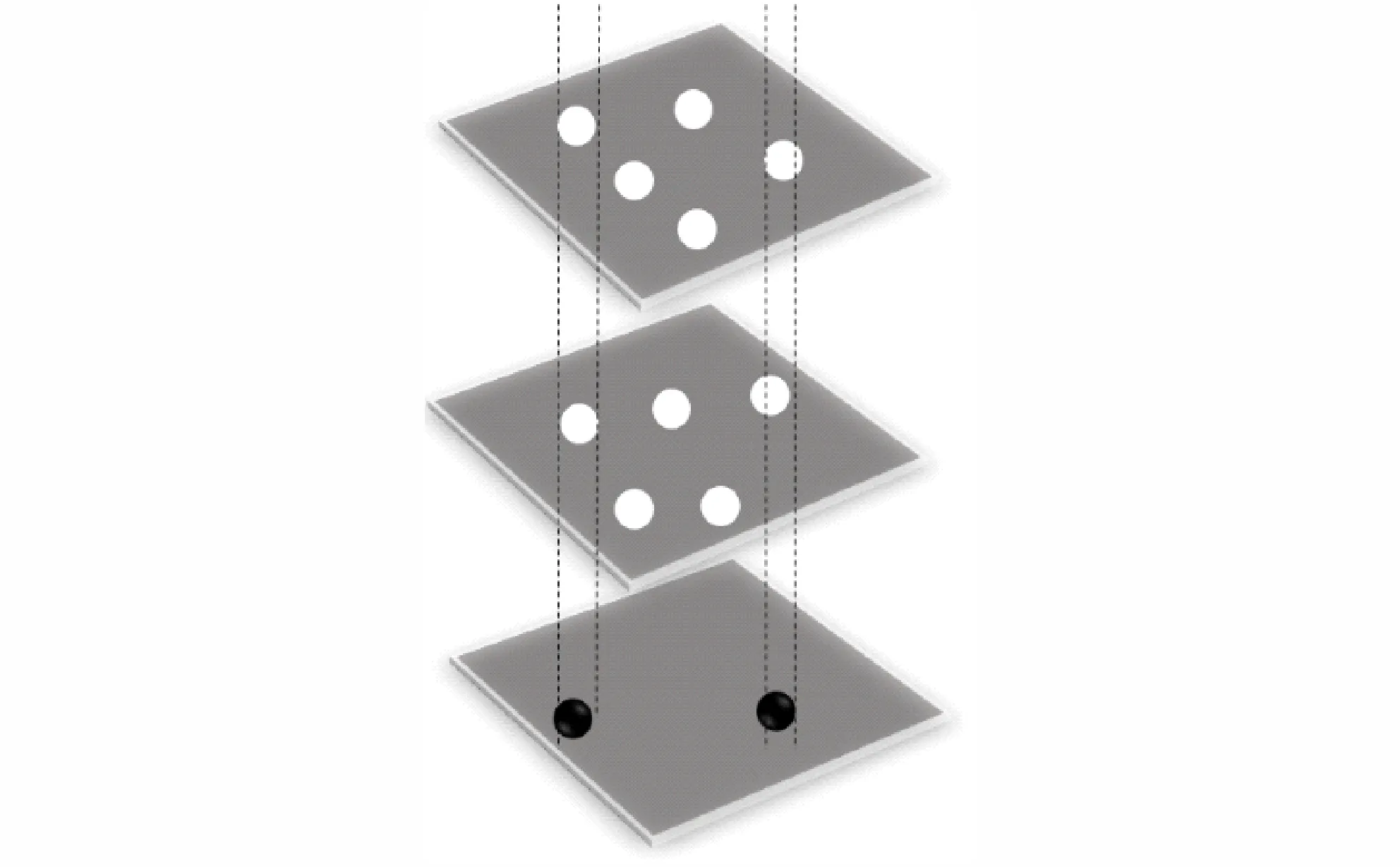
图2 相邻层分子在投影区域的重叠部分Fig.2 Overlapping part of adjacent layer molecules on the projection plane
2.2 压缩
为模拟真实情况下含能材料受到撞击时所产生的形变,对晶胞沿着撞击面进行压缩。假设分子为刚性即在撞击下不变形,只是压缩分子质心。由于分子晶体中分子间的范德华作用较弱,当受到撞击时,主要是分子间距离变化,由于分子本身相对刚性较高其变形可以近似地忽略。具体步骤如下:
设压缩的压缩比率为r(r>0),晶胞的晶格常数为a,b,c,撞击面的晶面指数为(jkl)。参考实际情况j,k,l≥0。注意到由于晶面指数的定义,j,k,l 不能同时为零。任取晶胞中一原子A,进行压缩前坐标为(x,y,z),进行压缩后坐标为(x',y',z'),由撞击面晶面指数j、k、l 及压缩比r 可得原子各轴压缩比分别为ra、rb、rc,则有:

2.3 旋转
由于每一个滑移系的滑移面和滑移方向上的空间位阻存在差别,为了保证算法的一致性需要建立新的空间直角坐标系,使得滑移方向为新坐标系的X 轴正方向,滑移面为新坐标系的XOZ 平面,如图3 所示。
在对晶胞进行压缩后需要对晶胞进行旋转。该步输入的信息为滑移面{pqr}以及滑移方向
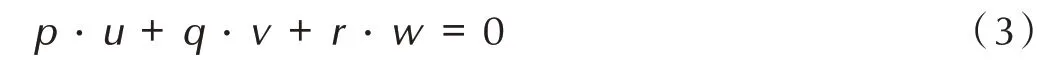
压缩后坐标系的三条坐标轴为X、Y、Z 轴,旋转后坐标系的三条坐标轴为X'、Y'、Z'轴。则压缩坐标系原子A 坐标仍记为为(x,y,z),旋转后的坐标记为(x',y',z'),旋转之前有:

旋转后,根据原滑移系与旋转后的滑移系{010}<100>各轴之间的夹角,计算出在旋转后的坐标系下晶胞内各原子在各轴最大及最小坐标:x'min,x'max,y'min,y'max,z'min,z'max。
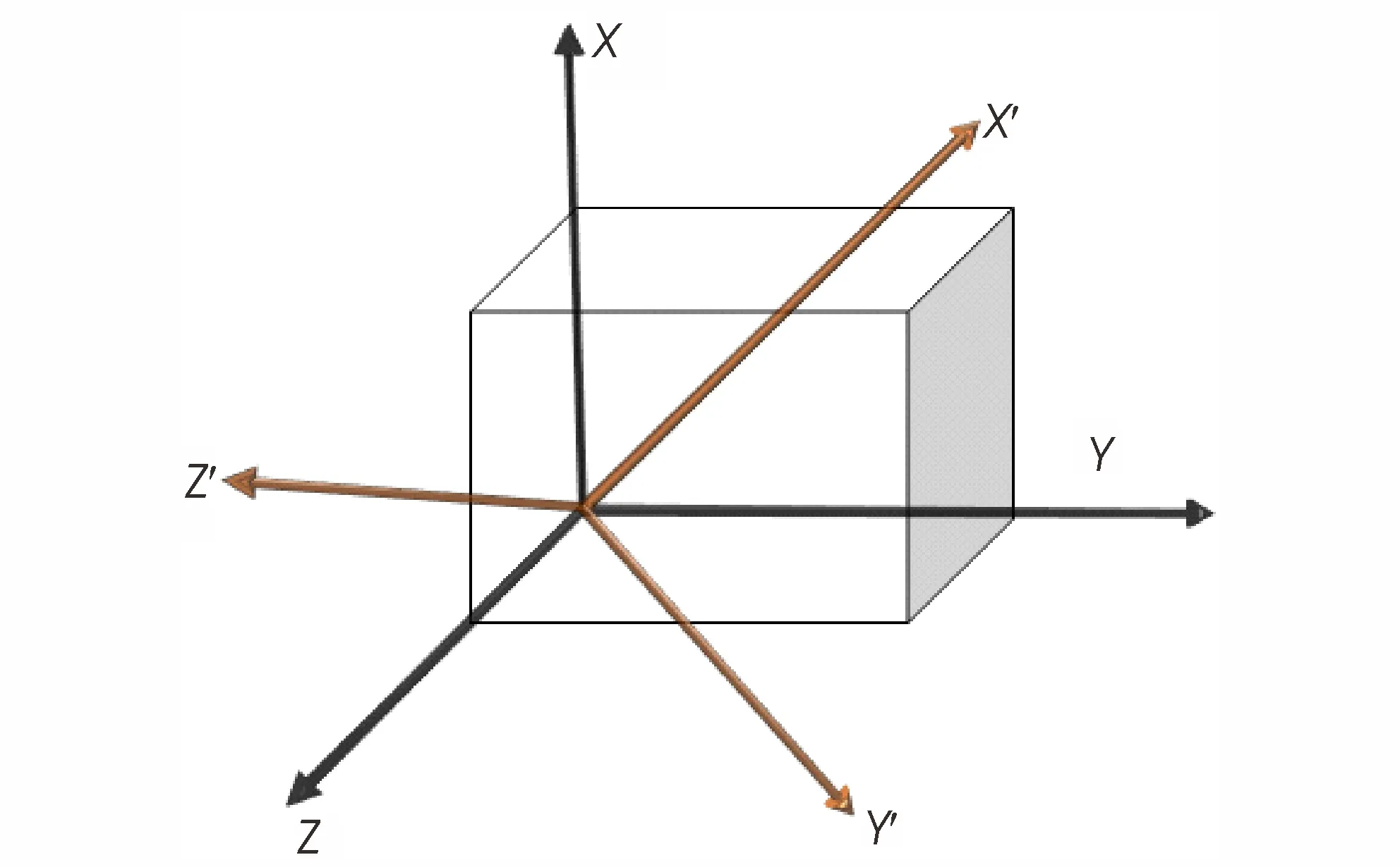
图3 原坐标系与新坐标系示意图Fig.3 Schematic diagram of original coordinate system and new coordinate system
2.4 分层
在实际的剪切形变过程中,在滑移方向上相邻的分子之间的碰撞是影响含能材料感度的重要因素。旋转坐标轴后,按照垂直于剪切滑移面的方向以分子质心的x 坐标对分子进行分层,并且假设归属于同一层内的分子无法碰撞。分层时如两相邻分子质心x 坐标不大于质心x 坐标相差最大的两分子质心x 坐标差值的5%,则将两分子归属同一平面内。
2.5 投影
在剪切形变过程中,晶胞内的分子沿着滑移方向,即X 轴正方向运动并发生碰撞,为了定量计算不同分子层间碰撞的剧烈程度,将分子层投影到YOZ平面上。投影区域设为矩形[y'min,y'max]*[z'min,z'max]。将投影区域细分为数量ny*nz个最小单元格组成的矩形。则Y 轴上步长为(y'max-y'min)/ny,Z轴上步长为(z'max-z'min)/nz。投 影 区 域 被 划 分 为ny*nz个 边 长 为(y'max-y'min)/ny,(z'max-z'min)/nz的小矩形。记所有的小矩形构成的集合为R={rij},i=1,2…,ny,j=1,2,…,nz。
分子层是由若干个分子组成的,而每个分子包含m 个原子,每个原子在空间中是一个以该原子坐标为球心,原子半径为半径的球。每个原子投影到YOZ 平面上之后实质上是一个圆。由于分子层的不同原子在投影区域内所形成的圆是相交的且有可能多个圆相交导致计算分子层所形成的面积较为复杂,因此使用ny*nz矩形的面积之和对分子层的投影面积进行近似。
任取某一分子层Lk,对于任意分子Mj属于Lk,任意原子A 属于Mj,则A 属于Lk。设Lk在YOZ 平面上的投影所对应的小矩形的集合为Sk。选取如下方法求Sk:
rij是划分的最小方格的中心点,对于在分子层Lk内的原子A,若划分的最小格子中心点在A 所投影的YOZ 平 面 上 的 圆 内,则 将rij计 入Sk.。如 图4 所 示,r_ij和r_(i+1)j不属于Sk,r_i,(j+1),r_(i+1)(j+1)属于Sk。Sk集合对应的中心点数即对应的最小方格数与投影区域全部最小方格数量之比即为SHI。
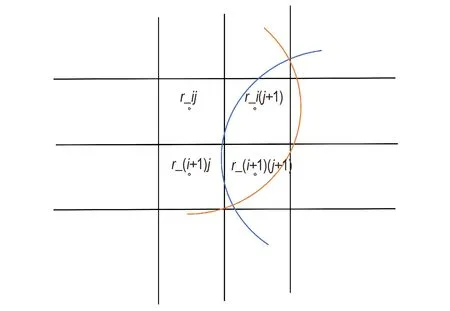
图4 投影方法示意图Fig.4 Schematic diagram of projection method
设晶胞经过压缩与旋转并按照分子质心的x 坐标排序后形成了t 个分子层,对每个分子层进行投影后,得到每一个分子层中被包含在原子投影中的最小方格中心格点的集合Si。随后计算相邻分子层重叠的中心点,即为计算投影的重叠面积。设集合Gi是集合Si与集合Si+1,的交集,其中i=1,2,…,t-1。另外需要指出的是,晶胞在晶体内呈周期性排列,所以需要计算St与S1的并集,记为Gt。

2.6 滑移系的自动搜寻
考虑某一撞击面(pk,qk,rk)中pk,qk,rk不同时为0。希望通过计算机自动搜寻np个滑移面,并在每个滑移面上搜寻nd个滑移方向作为备选滑移系。事实上,对于一个晶胞,低指数面方向上原子排布更密集,通过枚举法达到自动搜寻滑移系的目的。
3 计算结果与分析
3.1 投影算法的评判
构造如下的简单晶胞,晶格常数为a=b=c=10 Å,晶胞内有两个分子M1,M2。每个分子由四个原子组成,设为Ai,i=1,2,…,8,其中,A1,A2,A3,A4属于M1,A5,A6,A7,A8属于M2,原子半径均为1。8 个原子在晶胞内的坐标分别为A1(1,1,1),A2(1,9,1),A3(1,1,9),A4(1,9,9),A5(9,1,1),A6(9,9,1),A7(9,1,9),A8(9,9,9)。不 对 晶 胞 进 行 压 缩,同 时 滑 移 面 为{010},滑移方向为<100>,即不旋转晶胞,直接进行分层与投影。该晶胞分成两层,投影区域为[0,10]*[0,10],每个分子层在投影区域内的投影如图5所示。

图5 构造简单晶胞分子层投影示意图Fig.5 Schematic diagram of molecular layer projection in a single unit cell
该晶胞的两分子层在投影区域内的重叠部分面积为:
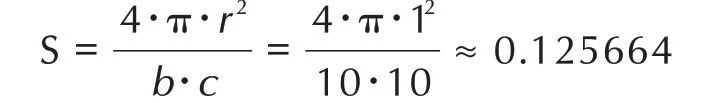
在不同的划分精度ny,nz,投影算法的空间位阻指数计算结果见表1。
在ny=nz=100 时,SHI 为0.1264,误 差 为0.6%。ny=nz=500 时,该方法的误差为0.08%,在ny,nz不太大时,近似计算方式就可以得到较良好的模拟结果。
3.2 RDX 晶体的SHI 与CS⁃RD 模拟结果比较
选取α-RDX 单晶的晶格常数为a=13.182 Å,b=11.574 Å,c=10.709 Å[6]。
垂直于下列五个低指数平面的撞击面:(100),(210),(111),(110)和(120)。参照An 等[5]的实验,对5 个撞击面选择计算主要滑移系:(A)(210)/{120}<-210>;(B)(100)/{-110}<110>;(C)(111)/{021}<100>;(D)(120)/{010}<100>;(E)(110)/{010}<100>,同时计算非主要滑移系的SHI 作为对照。对RDX 晶体 的CS-RD 实 验 表 明,(A),(B)为 敏 感 滑 移 系,而(C),(D),(E)为非敏感滑移系。由于非主要滑移系在剪切形变的过程中较少产生,因而非主要滑移系属于敏感或非敏感晶系未被纳入讨论。
从表2 对比可得敏感滑移系1,7 的空间位阻指数显著大于非敏感滑移系9,16,20 的空间位阻指数。
为 与An 等[5]报 道 的RDX 的CS-RD 对 比,同 样 选定压缩比(r)为0.1 和0.2。压缩比增加则系内晶体分子碰撞后温度与NO2含量都会相应增加。对滑移系的SHI 计算结果分别见表2 和表3。
从表3 可得敏感滑移系1,5 的空间位阻指数显著大于非敏感滑移系11,17,21 的空间位阻指数。
3.3 PETN 晶体的SHI 与CS⁃RD 模拟结果比较
所研究PETN 单晶的晶格常数为a=13.29 Å,b=13.49 Å,c=6.83 Å[7]。
为 与Zyben 等[3]报 道 的PETN 的CS-RD 对 比,选定压缩比ratio=0.1。
从表4 可得敏感滑移系1、3 的空间位阻指数显著大于中等敏感以及非敏感滑移系4、7、8 的空间位阻指数。
3.4 β⁃HMX 的SHI 与CS⁃RD 模拟结果比较
所研究β-HMX 单晶的晶格常数为a=6.5209 Å,b=10.7610 Å,c=7.3063 Å[8]。
为 与ZHOU 等[9]报 道 的β-HMX 的CS-RD 对 比,选定压缩比ratio=0.17。
对非正交滑移系的计算,需要用atomsk 软件将非正交晶系转换为正交晶系。以单斜晶系中β-HMX 为例,结果见表5。
非正交晶系SHI 计算结果和CS-RD 计算偏差较大,因此需要详细分析对于非正交转为正交晶系与初始晶系为正交晶系之间的区别,此外亦可能是在SHI算法中未考虑化学因素对碰撞所产生的影响。
3.5 SHI 与撞击后8 ps 体系温度以及撞击后10 ps 时NO2/RDX 含量的比较
An 等[5]基于RDX 的CS-RD 计算了每个滑移系在8 ps 时的反应温度与10 ps 时NO2/RDX 含量。这两个数据可以体现反应的剧烈程度,即8 ps 体系温度及10 ps 时的NO2/RDX 含量越高滑移系的敏感程度越高。CS-RD 计算结果与SHI 比较见表6(r=0.1),其相应的图示见图6。
如表6 和图6 显示,5 个主要滑移系的SHI 与8 ps时的温度,10 ps 时的NO2/RDX 大体上趋势相同,可有效地区分敏感与非敏感滑移系,敏感滑移系的SHI 显著大于非敏感化学系SHI。在r=0.1 时RDX 的5 个主要滑移系的SHI 与CS-RD 反应体系在8 ps 时的温度相关系数为0.9160,即SHI 与CS-RD 反应体系在8 ps 时温度呈强相关性。SHI 与CS-RD 反应体系10 ps 时NO2/RDX 含量相关系数为0.8134,即SHI 与CS-RD 反应体系10 ps NO2/RDX 含量呈强相关性。撞击后8 ps体系温度及10 ps NO2/RDX 含量表明敏感滑移系(A)、(B)较非敏感滑移系(C)、(D)、(E)反应更剧烈。
3.6 各正交晶系含能材料的SHI 与落锤实验测得撞击感度比较
以表2 的RDX 的22 个低指数晶面滑移系为例,计算PETN,BTF[10],TNT[11]对应的SHI 及22 个滑移系的平均SHI 并与落锤实验测得的H50(用2.5 kg 的落锤仪对含能材料进行试验,在达到50%爆炸几率时的落高)比较,结果见表7 及图7。
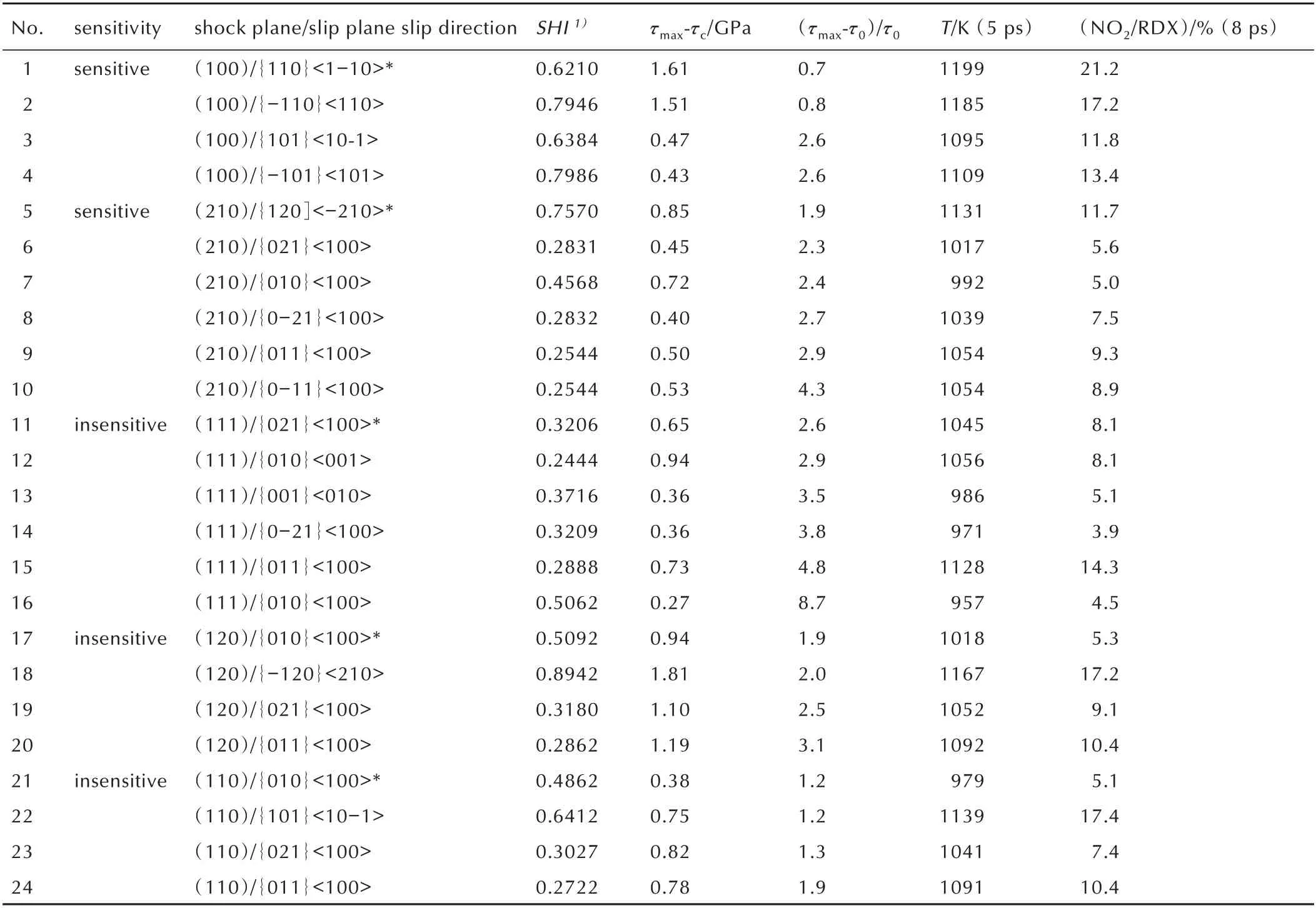
表3 r=0.2 时24 个滑移系的SHI 与CS-RD 结果[5]比较Table 3 Comparison of SHI and CS-RD results for 22 slip systems at r=0.2

表4 r=0.1 时8 个滑移系的SHI 与CS-RD 结果[3]比较Table 4 Comparison of SHI and CS-RD results for 8 slip systems with r=0.1
对不同含能材料的撞击感度进行排序的方法之一是根据剪切壁垒最小原理[1-5],按照能量判据选择在撞击作用下最容易发生滑移的晶面,然后比较主要的滑移面中最低SHI。然而目前对BTF 和TNT 没有合适的力场模拟,没有公开的对TNT 和BTF 关于CS-RD 的报道,因此无法准确获知TNT 和BTF 主要滑移面。对于当前无法获取主要滑移面的体系,可假设低指数密排面为可能的滑移面,低指数密排方向为可能的滑移方向。对22 个低指数滑移系计算SHI,然后利用SHI 平均值判断撞击感度大小。例如,图7 为PETN、BTF、RDX、TNT4 种“含能材料0.1”压缩剪切后22 个滑移系的SHI;它们的平均SHI 由大至小依次为0.8707,0.7940,0.4228,0.0924(表7)。相应的,表8 中给出实验H50由小至大排列为PETN、BTF、RDX、TNT。四种含能材料的22 个滑移系的平均SHI 与其落锤实验对应的H50的相关系数为-0.9061,呈强负相关性,即正交晶系含能材料的撞击感度越高,对应的平均SHI越大。由此推断,这种策略可以适用于对广泛的含能分子晶体进行相同基准下的系统比较和搜索优化设计,对于推测正交晶系含能材料的撞击感度具有较高的参考价值。

表5 r=0.17 时8 个滑移系的SHI 与CS-RD 结果[9]比较Table 5 Comparison of SHI and CS-RD results for 8 slip systems at r=0.17

表6 5 个主要滑移系的SHI、8 ps 时的温度以及10 ps 时的NO2/RDX 含量[5]Table 6 SHI of the five main slip systems,temperature at 8 ps,and NO2/RDX content at 10 ps
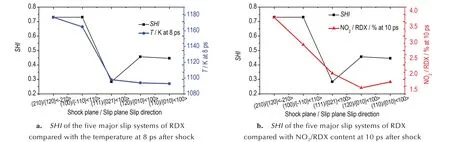
图6 RDX 的5 个主要滑移系的SHI 与碰撞后8 ps 时的温度及10 ps 时NO2/RDX 含量的关系Fig.6 SHI of the five main slip systems of RDX compared with the temperature at 8 ps and NO2/RDX content at 10 ps after shock
3.7 原子半径的影响
在空间位阻指数的计算过程中,原子的半径会对SHI 计算结果绝对值造成影响。原子半径分为轨道半径、范德华半径、共价半径等。本文所研究的含能材料的晶胞一般为分子晶体,起作用的半径为范德华半径。Pauling[20]于20 世 纪30 年 代 提 出 了 范 德 华 半 径及一组原子的范德华半径,但在随后的近100 年里,化学家们根据不同的理论基础给出了不同的计算结果。Bondi[21]于1964 年 根 据 晶 体 结 构 数 据、原 子 的 碰 撞 界面等数据得到了一组范德华半径。 1994 年,Allinger[22]根据分子力学得出了孤立状态下的原子的范德华半径,他的计算结果较由晶体结构数据得出的计算结果偏大。胡盛志等[23]在2003 年以晶体中原子的平均体积为出发点,提出了另一组计算结果。此外将原子的共价半径也纳入考量,以RDX 晶体所包含的H、C、N、O 原子为例,四组范德华半径及共价半径见表9。
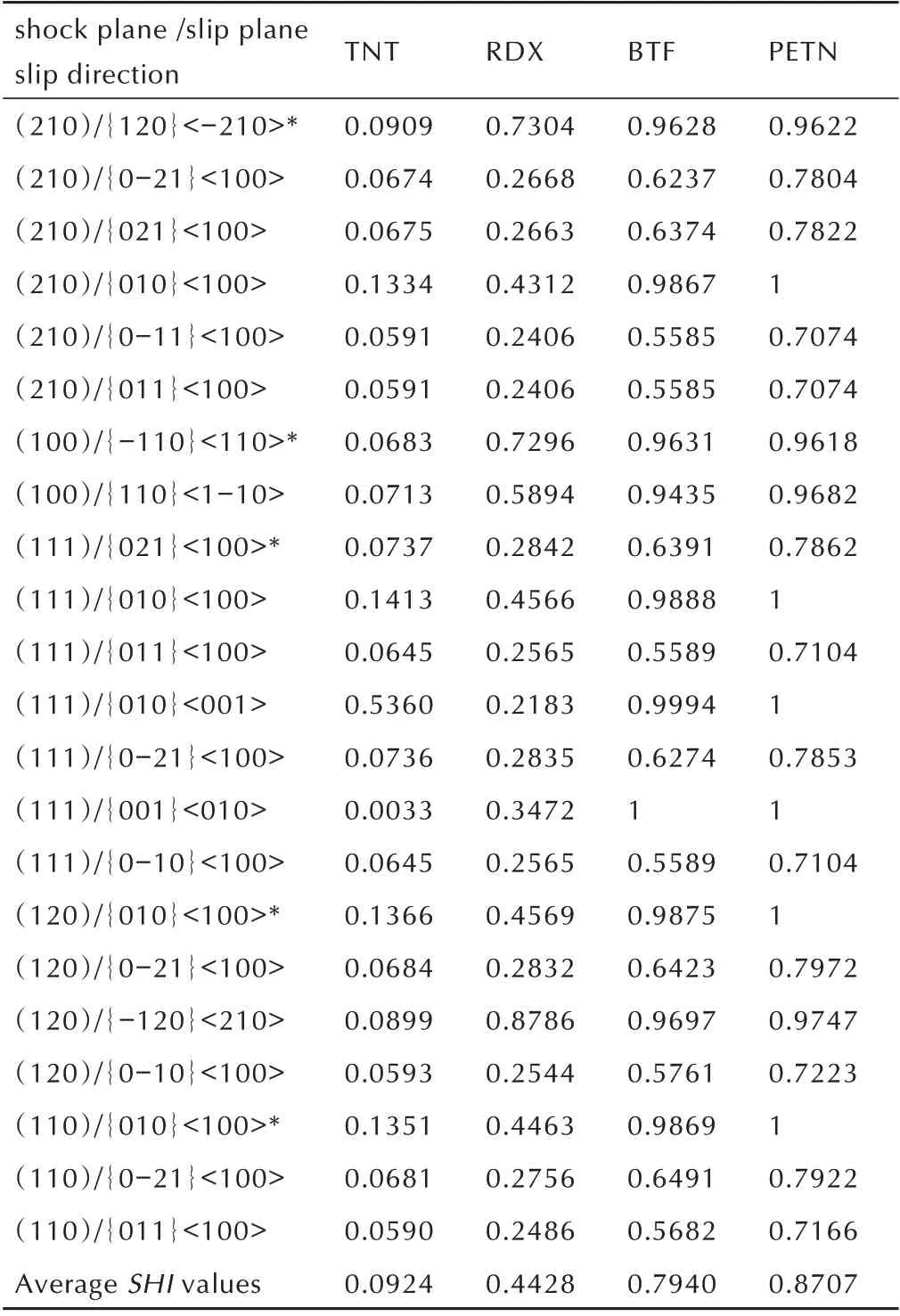
表7 RDX、PETN、BTF、TNT 在22 个低指数晶面下的SHI 及SHI 均值Table 7 SHI of RDX,PETN,BTF,TNT in 22 low-index crystal plane slip systems and the average SHI values
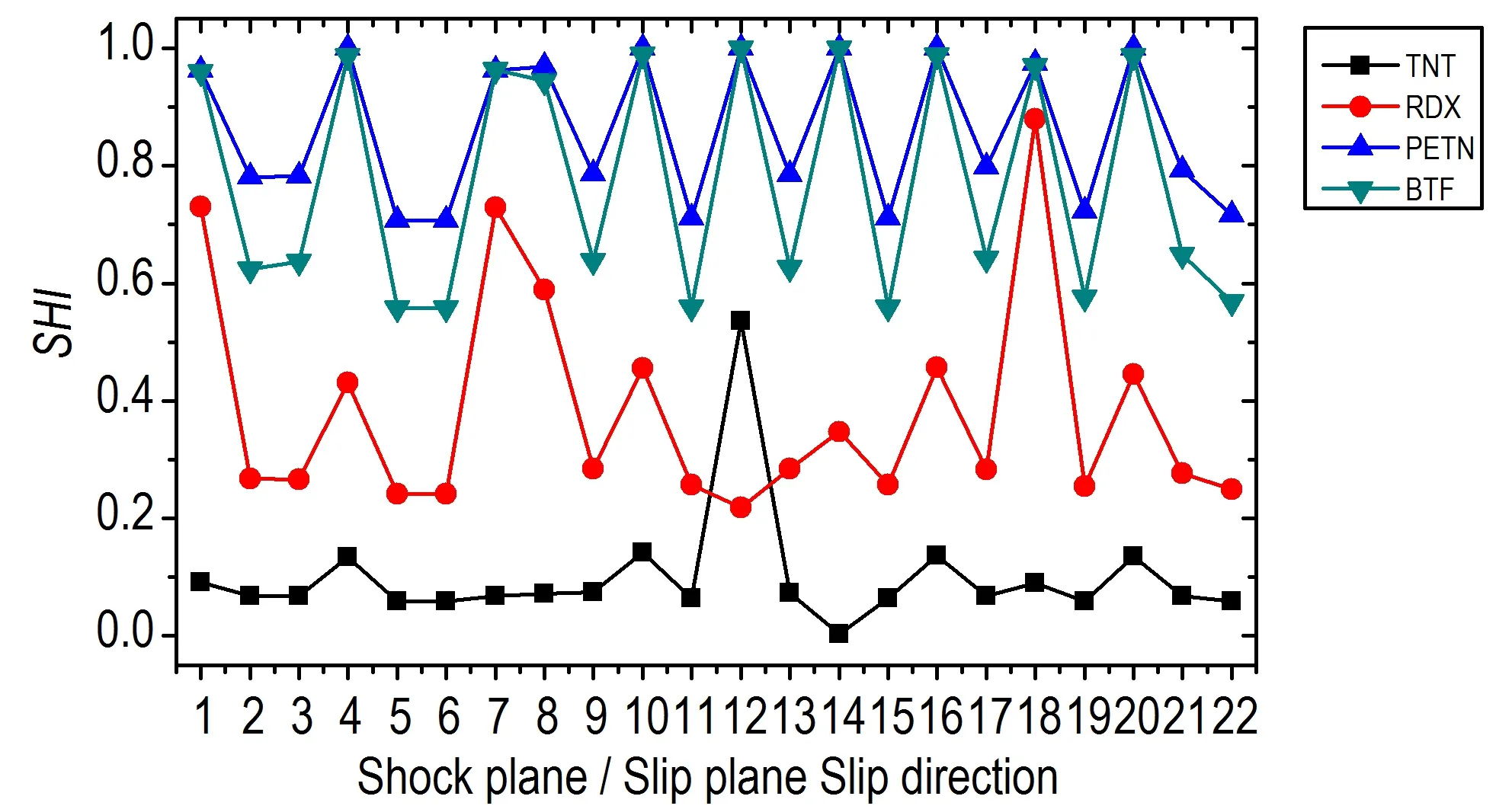
图7 对含能材料10%的压缩剪切后22 个滑移系的SHI 对照Fig.7 SHI comparison of 22 slip systems based on 10% compression shear of energetic materials
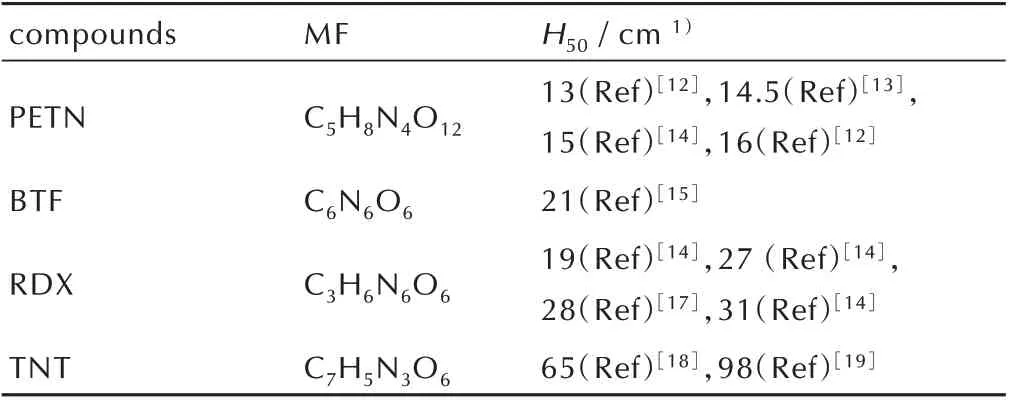
表8 PETN、BTF、RDX、TNT 的H50Table 8 H50 of PETN,BTF,RDX and TNT
为研究不同的原子半径对空间位阻指数的影响,计算了各原子半径下压缩比为0.1 时的SHI,结果见表10。
由表10 可得原子半径标度的选择并不会定性改变对敏感与非敏感滑移系的区分。非敏感滑移系(C)、(D)、(E)的空间位阻指数仍小于敏感滑移系(A)、(B)的空间位阻指数。
研究中原子半径采用Allinger 的计算结果。
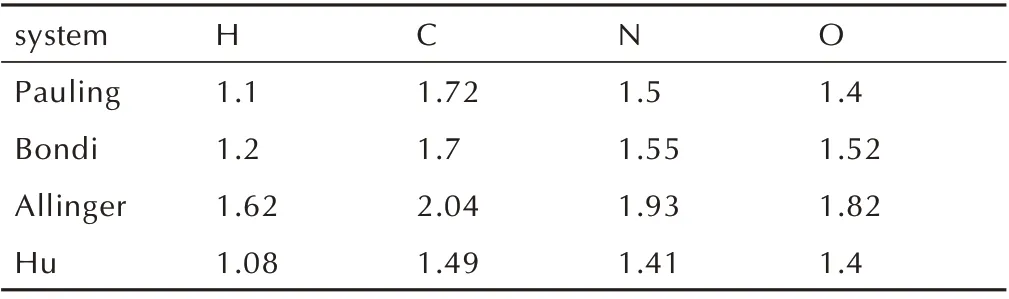
表9 H、C、N、O 的原子半径[23]Table 9 Atomic radius for H,C,N,O Å
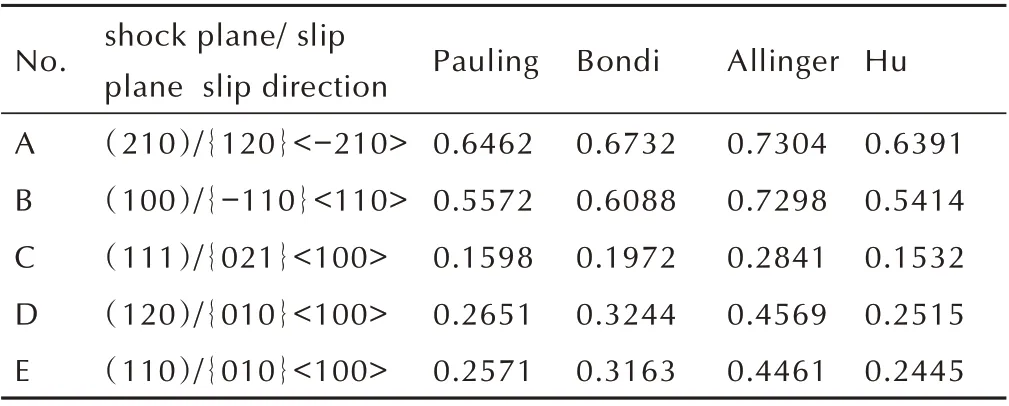
表10 不同原子半径的SHI 计算结果Table 10 SHI with different atomic radius
4 结论
设计了含能材料空间位阻指数计算算法,并使用Python 语言开发了相应的计算机程序。应用于几种典型的正交晶系含能材料PETN、BTF、RDX 和PETN 等算出其SHI,并与压缩-剪切反应动力学的模拟结果比较表明:(1)空间位阻指数与反应分子动力学模拟所得结果如温度、二氧化氮含量正相关。(2)对于正交晶系含能材料多个滑移系的SHI 的计算结果可知,SHI 大小与其撞击感度有明显的正相关。
文中提出的评价含能材料撞击感度的算法适用于正交晶系含能材料快速查找出敏感滑移系与非敏感滑移系,以及评价正交晶系含能材料中撞击感度的高低。算法中未考虑不同原子间碰撞化学因素的影响以及碰撞时的剪切应力能垒,原则上将来可扩展至非正交晶系含能材料。
基于空间位阻方法的感度评估不需要复杂耗时的分子动力学模拟计算,因此能被用于高效评估含能材料感度,尤其适合于高通量计算的含能晶体结构搜索和筛选,并可作为描述因子构建关联结构-感度的机器学习模型。本研究对于筛选高能量密度低撞击感度的含能材料具有一定的实用价值。
