西安市挥发性有机物(VOCs)扩散迁移与气象因素的研究

强逸凡，吴柳莹，张 洁，胡苇杭，冯 哲，黄光球

(西安建筑科技大学管理学院 陕西西安710055)

0 引 言

西安市作为陕西省省会、特大城市、关中平原城市群核心城市，近些年发展势头崛起，随之带来的是更多的环境问题。2019 年西安市政府发布了《西安市“铁腕治霾·保卫蓝天”2108—2019 三年行动方案(修订版)》，根据年西安市环境公报显示，西安市环境整体呈转好趋势，但空气污染物成分含量中首要污染物仍是细颗粒物(PM2.5)。因此，研究西安市挥发性有机物VOCs(Volatile Organic Compounds)扩散迁移与气象因素的关系极为必要。

此前，学术界已有多名学者对VOCs 扩散迁移与气象因素做了研究。张勇等[1]研究了枣庄市夏秋季挥发性有机物对环境空气质量影响；梁天池等[2]探究了工业区大气污染物的迁移扩散模型及其应用；江军[3]对黄土高原地区农业面源污染时空特征及与经济发展关系进行研究；魏巍[4]研究了中国人为源挥发性有机化合物的排放现状及预测未来发展趋势；石雪颖等[5]对北京市大气重污染过程中AQI 的时空扩散特征进行了研究并预测了其模型；余虎等[6]对西安市大气污染颗粒物自然驱散因素进行了研究；Emilio Sabia 等[7]对挥发性有机物特性及影响进行了进一步研究。

目前，我国大气污染面临着严重污染，固定源污染包括化石燃料、生物质(秸秆、木材)燃烧，溶剂使用、石油化工、炼钢炼焦等，移动源包括机动车、火车、飞机、轮船等公共交通工具，它们的尾气排放到大气中，导致大气环境污染日益严重。基于此，本文对气象自然因素对西安市挥发性有机物扩散迁移与气象因素的影响做进一步研究。

1 数据来源

本文2018 年、2019 年国控城市点PM2.5年平均值(图 1)来源于 2019 年西安市环境状况公报(http：//www.xa.gov.cn/gk/sthj/kqhj/5dae57a965cbd86d 496cb373.html)；2018 年、2019 年西安市月均温度、湿度及风速来源于中国空气质量在线监测分析平台(https：//www.aqistudy.cn/historydata/weixin.php)。

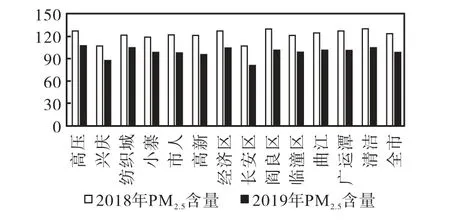
图1 2018年、2019年国控城市点PM2.5 年平均值对比图Fig.1 Comparison of annual average PM2.5 in statecontrolled cities in 2018 and 2019

2 相关研究方法

2.1 研究方法

通过做出温度(图2)、风速(图3)和PM2.5(图4)折线图及空气质量指数AQI(Air Quality Index)变化趋势图(图5)，发现随着温度、风速的升高及变大，会导致PM2.5含量变低及AQI 值变高，而VOCs 是形成PM2.5的重要前提物，且也在很大程度上影响AQI 的指数值，空气污染物中有 70% ～80% 的组成为PM2.5。为了揭示挥发性有机物和气象条件带来的影响之间的关系，本文采用Matlab 建立两者之间的线性回归方程，通过回归分析，初步认为温度对挥发性有机物具有线性影响。

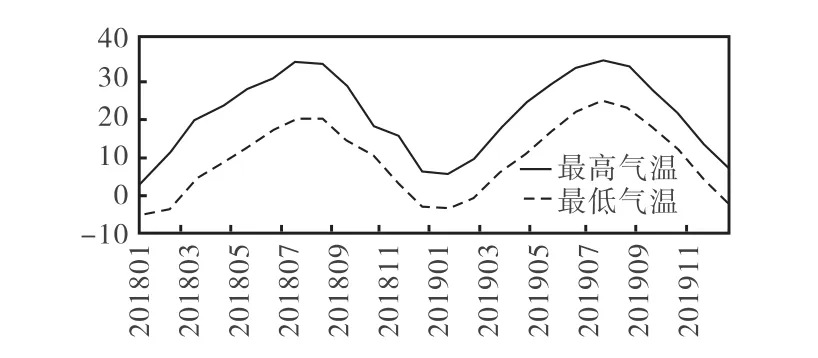
图2 2018—2019年西安月均最高气温和最低气温折线图Fig.2 Line graph of monthly average maximum and minimum temperatures in Xi"an from 2018 to 2019

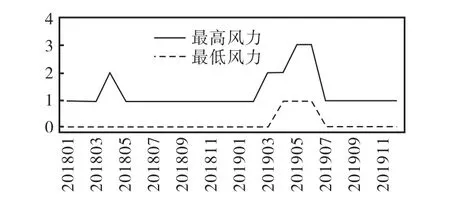
图3 2018—2019年西安月均最高风速和最低风速折线图Fig.3 Line graph of average monthly maximum and minimum wind speeds in Xi’an from 2018 to 2019

图4 2018—2019年西安市PM2.5 含量折线图Fig.4 Line graph of PM2.5 content in Xi’an from 2018 to 2019

图5 2018—2019年西安市AQI指数变化折线图Fig.5 Line graph of change in AQI index in Xi’an from 2018 to 2019

2.2 自变量的选择

本文选择气象影响因素中最主要因素之一：温度。通过分子的热运动可知，温度越高分子无规则运动越快，扩散越快；其次是风速，风速加快，会影响气体局部的压强，根据理想气体状态方程PV＝nRT，物质的量(n)不变、体积(V)不变，当压强(P)升高时，则温度(T)也会随之升高。微观体现即为分子的热运动加快，故温度(T)升高，分子运动加快，则会影响大气中PM2.5的含量和AQI 指数的变化值(表1)。

2.3 因变量的选择

VOCs 是形成PM2.5的重要前体物，也在一定程度影响AQI 的数值，VOCs 含量中70%～80%都是PM2.5，说明PM2.5与VOCs 的关系密切，变化相关。因为产生VOCs 的来源多、广、杂，在收集数据方面会有很大的困难与不便，所以本文选择PM2.5和AQI作为监测VOCs 扩散与迁移的指标，依据空气中PM2.5的变化和空气质量指数进行研究(表2)。

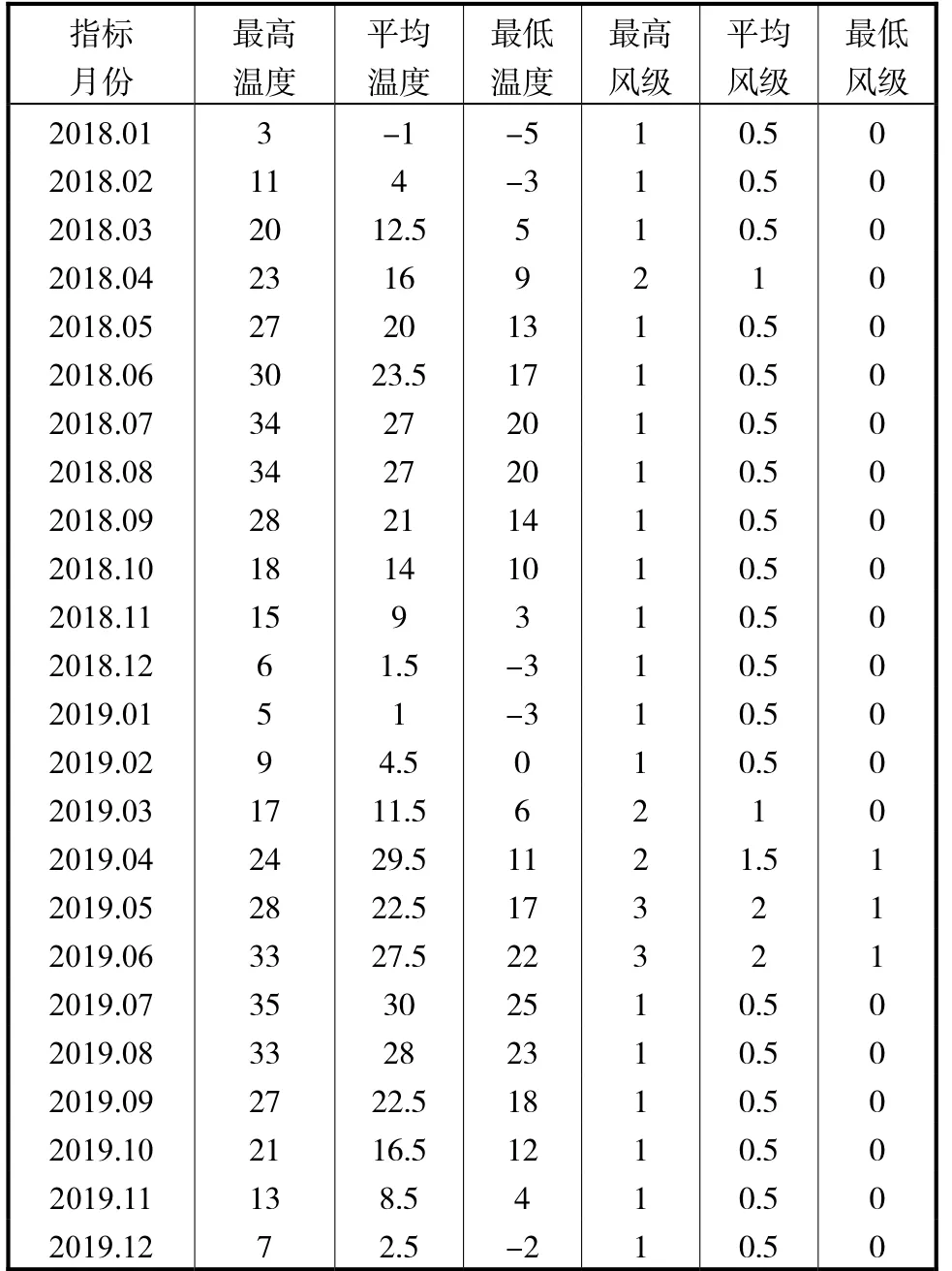
表1 2018—2019年西安市温度、风级统计数据Tab.1 Statistics of temperature and wind speed in Xi"an from 2018 to 2019

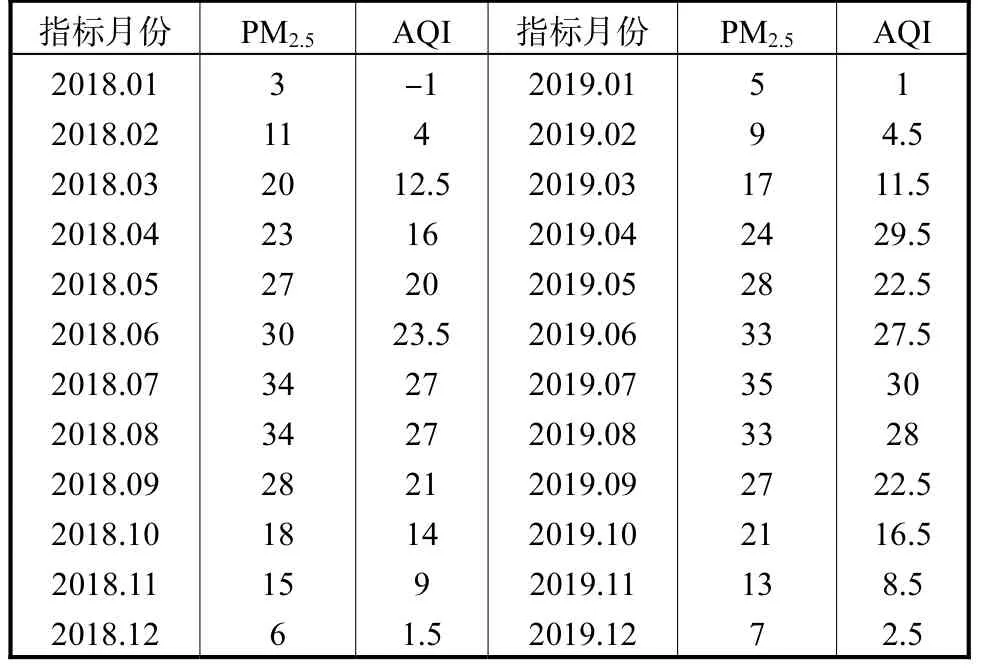
表2 2018—2019年西安市PM2.5、AQI统计数据Tab.2 Statistical data of PM2.5 and AQI in Xi’an from 2018 to 2019

3 计算分析

通过分析初步认为温度与风力与PM2.5的含量呈线性关系，使用SPSS 工具建立线性回归方程。

对表3、表4 及图1 至图4 用下列表达式：

对表达式(1)进行线性回归分析，结果如表5所示。

表3 自变量相关自然指标Tab.3 Natural indicators related to independent variables

表4 因变量相关自然指标Tab.4 Natural indicators related to dependent variables

表5 模型汇总bTab.5 Model summary

由表5 可知：相关系数R＝0.894，表明自变量(T、S)和因变量(PM2.5)之间存在着高度线性相关性。

判定R2＝0.800，说明回归平方和占总离差平方和的比例为80.0%，用T 和S 可以解释x1即空气中(PM2.5)的变动比例为80.0%，说明该回归的效果较好，本观测值的拟合程度较好。

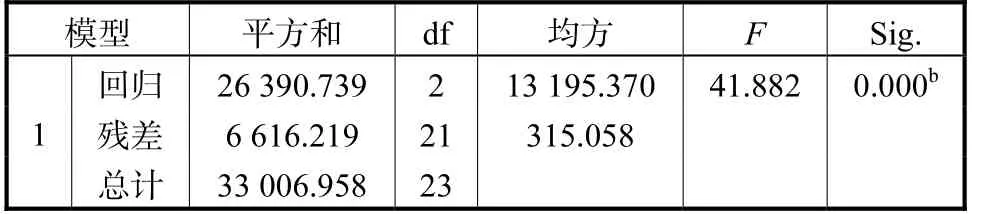
表6 Anovaa(PM2.5)Tab.6 Anovaa(PM2.5)

对表6 结果分析如下：

SSR(回归平方和)＝26 390.739

SSE(残差平方和)＝6 616.219

F(拟合显著性)＝41.882

P(不拒绝除假设的程度)＝0.000＜0.05(显著性表示自变量对因变量的影响程度，小于0.05 表示有显著影响，说明该模型具有95%的把握认为回归方程显著)。

对表7 结果分析如下：

如何求得P＝0.01＜0.05，所以选择表7 中B 列数值，那么可以将表达式(1)写为如下回归方程：

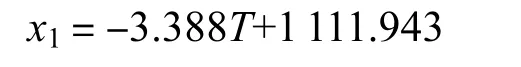
若P＞0.05，则该回归方程不含常数项，就要选择标准系数检验其余系数；如表6 所示，P＝0.449＞0.05，剔除变量S，这个变量S 不能进入该方程。

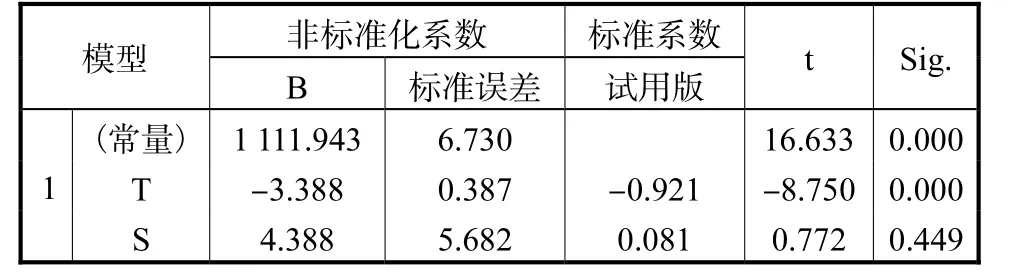
表7 Anovaa(PM2.5)Tab.7 Anovaa(PM2.5)

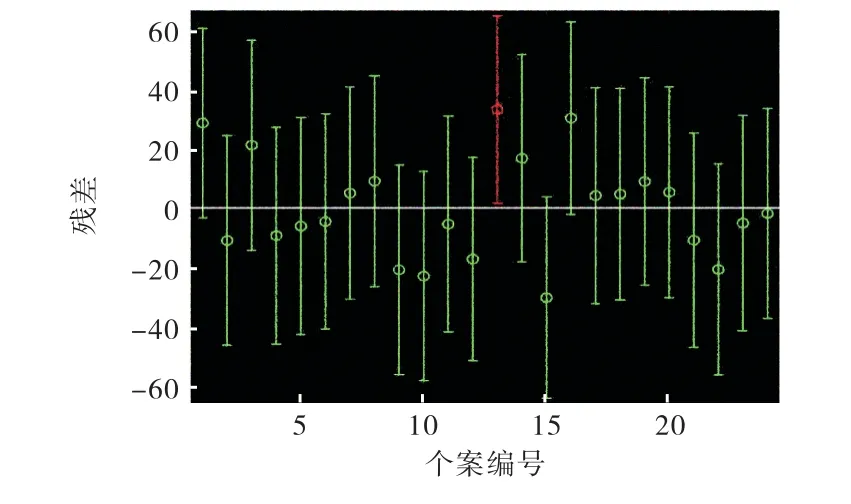
图6 残差个案次序图Fig.6 Sequence diagram of residual cases

由表达式(1)生成残差个案次序图，如图6 所示，可知第13 个点落在中轴线的带状区域之外，说明该点(1，142)是奇异点应该删除，删除后，重新进行运行得到残差个案次序图，如图7 所示。

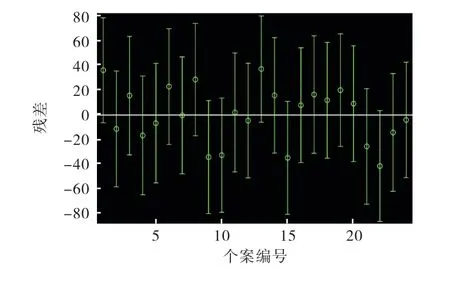
图7 残差个案次序修正图Fig.7 Sequence correction diagram of residual cases

根据重新运行出的残差个案次序修正图(图7)，可以判断出残差个案均落在中轴线带状区域以内，说明无奇异点。由图8 可知：残差值都在置信区间上限、下限范围内，代表回归模型正常，所以表达式(1)的回归模型正常。

对表达式(2)进行线性回归分析，得到结果如表8 所示。由表8 可知：相关系数R＝0.741，表明自变量(T、S)和因变量(AQI)之间存在着线性相关性。

但因为R2＝0.550，即回归平方和占总离差平方和的比例为55.0%，用T 和S 可以解释空气中(AQI)的变动的比例为55.0%，说明该回归的效果一般，本观测值的拟合程度不佳，据此认为AQI 与T、S 之间无显著关系，剔除表达式(2)。

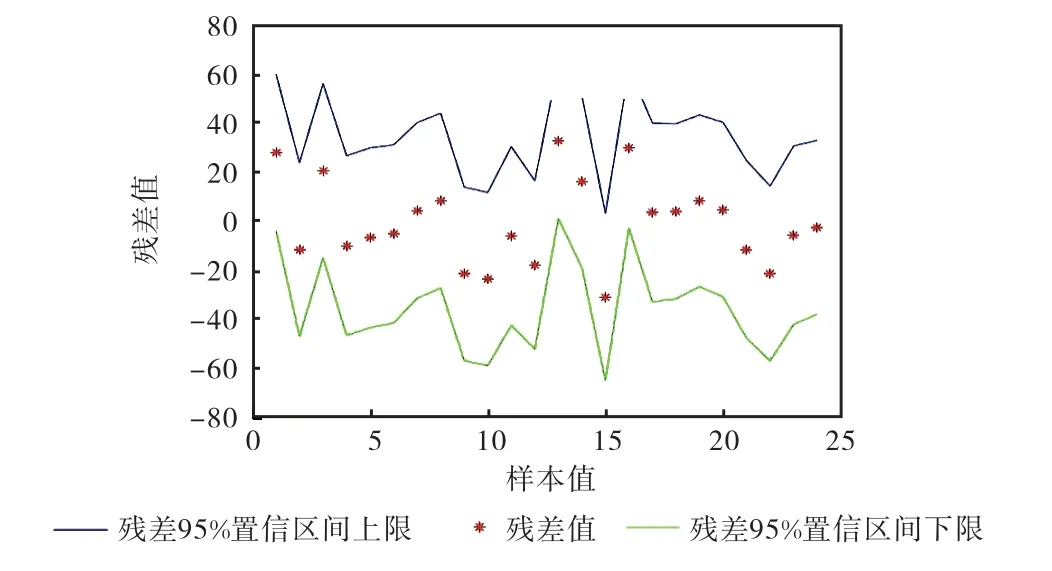
图8 残差值图Fig.8 Residual value graph

表8 模型汇总bTab.8 Model summary

通过建立多元线性回归方程，发现挥发性有机物扩散迁移与气象因素呈负相关线性影响，即T 每增加1 ℃，空气中PM2.5的含量下降3.388 mg/m3。

4 结 论

近些年，在经济上，西安作为陕西省省会城市，发展走在全国城市前列；在环境上，西安位于我国西北区域，关中盆地，暖温带半湿润大陆性季风气候，四季分明，雨量适中。但近些年发展同时，大气环境遭到破坏，超过其最大承载力。在日后的发展中要增强对大气环境的治理与保护，加大大气环境治理和研究，降低各类有机物的排放。■