基于函数链神经网络的智能传感器非线性校正方法

徐桂林，黄 彦，孙振庭

(1.长春气象仪器研究所有限责任公司，长春 130102；2.长春希迈气象科技股份有限公司，长春 130102)

0 引言

随着电子技术、处理器技术和现场总线技术的发展，在工业现场的信号采集处理中，以微处理器为核心的智能传感器应用越来越广泛。这类传感器不仅可以对现场量进行采集与表征转换，还具有很强的数据处理和通信能力，使在前端对一次元件进行参数变换和非线性校正的构想成为可能[1]。

目前，对传感器非线性校正的方法有很多[2，3]。最常用的是查表法(分段线性插值方法)，在量程内将曲线分成很多段，每一段用直线代替曲线，分段直线近似逼近曲线，分的段数越多，近似精度越高。但同时占用的存储空间也越大，查表时间随之增长，因此该方法实时性不好，对于精度要求高的场合适用性较差。曲线拟合法是用n次多项式拟合传感器反非线性曲线，多项式系数一般采用LS算法及各种改进的LS算法确定，求解过程可能因噪声污染而无法求解出正确值[4，5]。基于神经网络的非线性补偿方法是近年发展起来的新型算法，利用传感器检测数据或标准分度表训练BP神经网络，得到传感器逆模型，进而使校正模型系统线性化，得到的网络可按一般线性特性处理，具有较好的适应性和较高的精度，但BP网络也存在收敛速度慢、隐层节点数选择困难和容易陷入局部最小等问题[6]。

1 智能传感器非线性校正模型

智能传感器的一般结构如图1所示。主要由3部分组成，一次敏感元件完成待采集物理量的电信号表征，信号调理电路对信号进行采集、滤波、放大及整形，A/D转换电路完成数字量转换，微处理器对A/D采集的数字信号进行数字滤波、非线性处理和标度变换，总线接口完成与上位计算机通信或其他网络节点的信号传输[7]。由于一般的敏感元件均具有非线性特性，加之调理电路和预处理电路引入的误差，会导致传感器输入-输出呈现非线性，因此需要进行非线性校正。

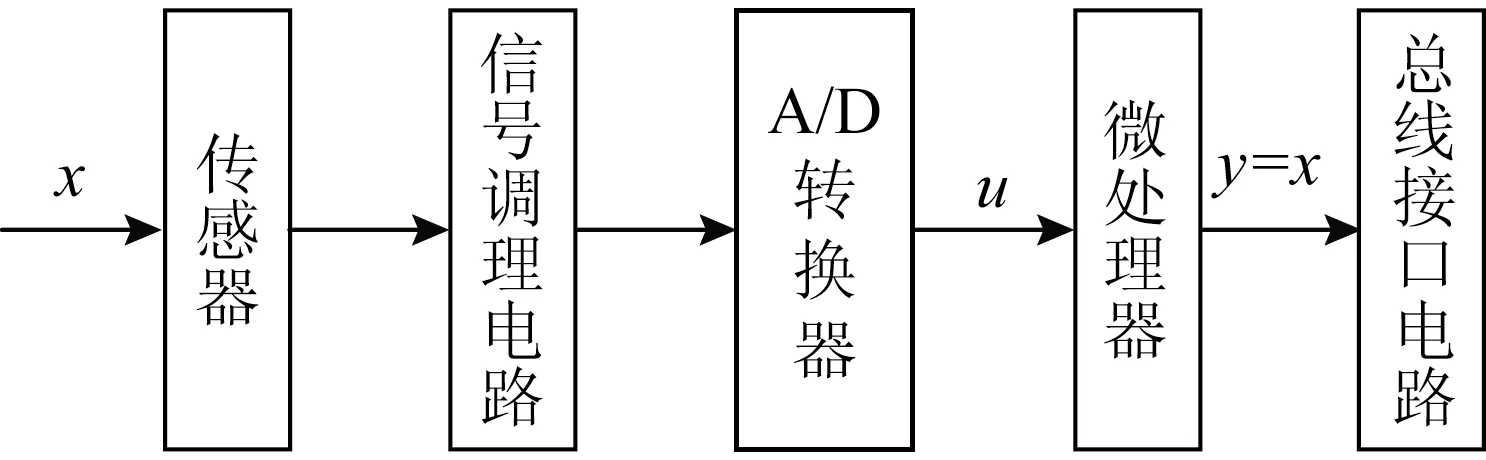
图1 智能传感器结构原理

传感器的非线性校正模型如图2所示。设被测量x经由一次敏感元件和A/D转换器后给微处理器的输出为u，可以描述为u=f(x)，也可以认为输入输出是一个函数关系。理想情况下u=kx，即输入输出为线性关系，但由于敏感元件的非线性特性，f(x)一般是一个非线性函数[8]。为此，可以在传感器和A/D转换后串联一个校正环节F，若校正环节的函数F具有与f相反的变换特性，即F=f-1，则：

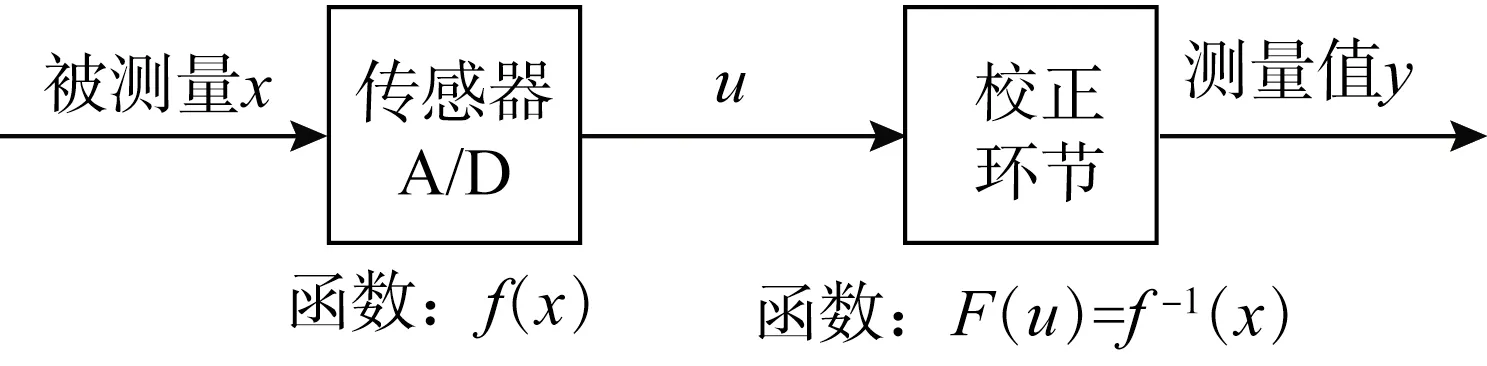
图2 非线性校正模型

y=F(u)=F[f(x)]=f-1[f(x)]=x

(1)

校正后的输出y与x成理想的线性关系。对敏感元件的非线性校正就是求取反非线性函数F。

通常F可近似表示为多项式形式：

F(u)=a0+a1u+a2u2+…+anun

(2)

式中：n为多项式阶数；a0…an为多项式系数。

2 函数链神经网络非线性校正算法

2.1 函数链神经网络非线性校正原理

函数链神经网络是一种引入非线性扩展函数的单层网络，通过对输入的函数进行扩展，将多层网络压缩成单层网络，使其具有很好的非线性映射能力，可避免BP网络陷于局部最小的问题[9，10]。对于反非线性函数F待定系数a0…an的求取可采用构造函数链神经网络的方法来实现，函数链神经网络的结构如图3所示。它能对输入的1组样本值进行学习，用学习迭代的方法对权值进行修正，通过多次学习，直至神经网络的输出值的误差均方值达到一个足够小的值，此时学习结束。最后得到的权值即为要拟合的多项式的待定系数。

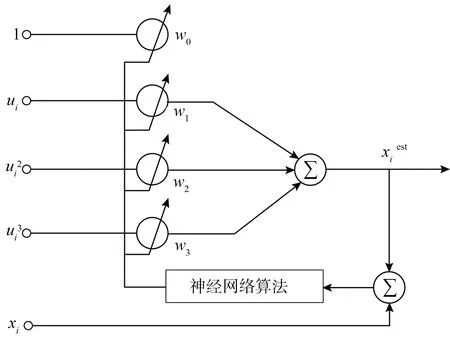
图3 函数链神经网络

2.2 函数链神经网络非线性校正方法步骤

在具体应用时首先要进行传感器标定试验，记录下标定点的传感器数据及A/D转换结果，在微处理器的软件中实现函数链神经网络算法，把A/D转换结果的标定值作为输入值，传感器所测的物理量为输出值，经过神经网络的学习得到要拟合曲线的系数，从而生成反非线性曲线方程，使用时通过反非线性曲线方程补偿传感器非线性。

函数链神经网络非线性校正步骤如下：

1)敏感元件及调理电路试验标定。在标准试验环境下，确定标定点数目N，通过试验标定实验数据得到N个标定点的输入、输出值。

2)列出反非线性特性拟合方程：

(3)

一般情况下，三阶多项式已能满足精度要求，取n=3，则

(4)

式中：a0～a3为待定系数。

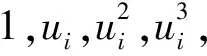
(5)

使估计误差[ei(k)]的均方值足够小，估计误差为：

(6)

权值调节式为：

(7)

当权值调节趋于稳定时，所得权值为：

Wj：W0，W1，W2，W3

即为多项式待定常数a0～a3：

a0=W0，a1=W1，a2=W2，a3=W3

3 实验研究

以气象科学中广泛使用的Pt100铂电阻温敏元件为例进行实验。0～200 ℃时Pt100热电阻的标定值如表1所示，其输入-输出特性存在着明显的非线性。在气象参数测量范围内可以使用式(8)近似描述其输入输出特性：

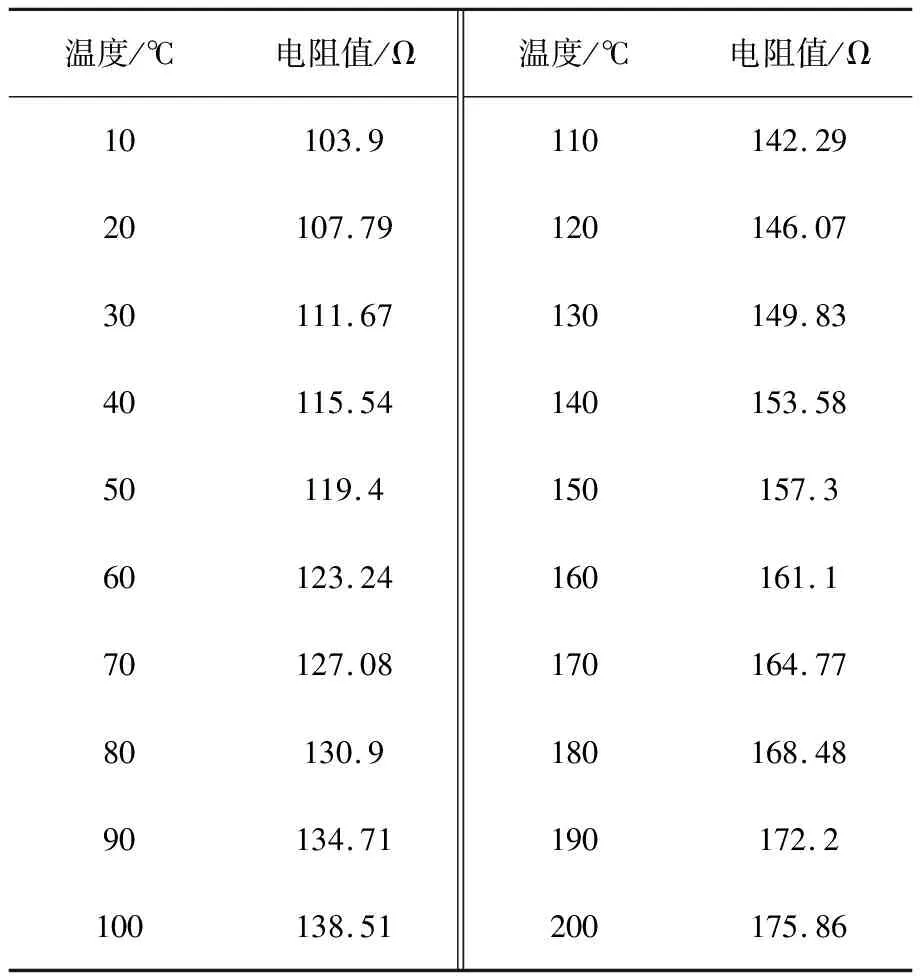
表1 Pt100铂电阻在0～200 ℃时的标定值

yi=W0+W1(x/xmax)+W2(x/xmax)2

(8)

根据上述校正方法，将Pt100电阻值的输出作为神经网络的输入xi，温度值作为输出yi，xmax取整数200，ui=xi/200。取n=2，赋连接权W0，W1，W2的初始值为(-1，1)之间的随机数，将Pt100的输入输出数据按顺序加入神经网络，用学习迭代方法对权值进行修正，其中学习因子η取为变数(0.95～0.4)。迭代运算后得到：W0=-244.8367，W1=467.7580，W2=43.5683。则Pt100铂电阻的反非线性函数为：

yi=-244.8367+2.33879x+0.001089x2

由反非线性曲线计算得到的温度值如表2所示。可见拟合值与标定值非常接近，最大相对误差不超过0.1%。

表2 计算值与标定值比较表 ℃

4 结束语

对于具有微处理器的智能传感器，可以根据文章提出的方法进行传感器出厂前的校准标定，以提高系统精度。如果考虑将一次敏感元件和前向数据采集通道作为一个整体，可以实现传感器自标定，也可以采用离线方式单独标定敏感元件。在Pt100热电阻实验中，假定阶数为3，忽略了高次项，可能对其他类型的一次敏感器件拟合精度不够，可以通过适当增加阶数来提高精度。该方法的局限性在于静态求取拟合参数，没有考虑传感器工作过程中的温漂和时漂影响，进一步的改进方向是在考虑传感器运行条件的前提下，实现在线非线性校正手段。