三次丢番图方程x3±33=pqy2的整数解
2021-04-06罗永亮
李 恒,杨 海,罗永亮
(西安工程大学 理学院, 陕西 西安 710048)
1 引言及主要结果
丢番图方程
x3±a3=Dy2(x,y∈N+,D>0且不含平方因子)
(1)
是一类重要的方程,对其整数解的探讨备受学者们的关注。近年来,杜先存[1-3]、管训贵[4-5]、张淑静[6-7]、杨海、李玉龙等[8-14]研究了a=1的情形,得到了很多有意义的结果。但是,对于a=3时,丢番图方程
x3±33=Dy2(x,y∈N+,D>0且不含平方因子)
(2)
的研究成果较少。1996年,倪谷炎得到了,当D不被6k+1型素数整除且不含平方因子,方程(2)的所有非平凡整数解[15];2008年,李双娥得到了D=7、13、19、26、31时方程(2)的全部整数解[16];2013年,高丽等得到了D=28时方程(2)的全部整数解[17];同年,钱立凯等得到了D在特定条件下方程(2)无整数解的2个充分条件[18]。2015年,王霞给出了D=14、31、35、37、38,、43时方程(2)的全部整数解[19]。本文利用初等数论方法并结合同余、Legendre符号的性质给出了D=pq时,丢番图方程x3±33=Dy2整数解的情况,得到下述结果:
定理1 设p=3(24r+19)(24r+20)+1为奇素数,r∈Z+且q≡5(mod 24),则丢番图方程
x3+33=pqy2
(3)
无正整数解。
定理2 设p=3(24r+19)(24r+20)+1为奇素数,r∈Z+且q≡5(mod 24),则丢番图方程
x3-33=pqy2
无正整数解。
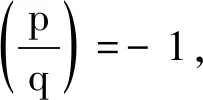
x3-33=pqy2
(4)
仅有平凡解(x,y)=(3,0)。
2 相关引理
引理1[6]若p为奇素数,p=3(24r+19)(24r+20)+1,r∈Z+,D1=2αq,其中α=0或1,q≡5(mod 6)为奇素数,则丢番图方程
x3±1=3pD1y2
+无正整数解。
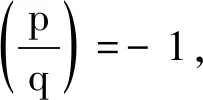
x3-1=3Py2
仅有平凡解(x,y)=(1,0)。
3 定理的证明
3.1 定理1的证明
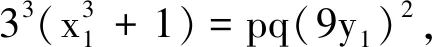
当x≢0(mod 3)时,此时有x+3≢0(mod 3)。设(x,y)是丢番图方程x3+33=pqy2的一组解,则gcd(x+3,x2-3x+9)=gcd(x+3,33)=1,故丢番图方程(3)可化为以下4种情形:
情形Ⅰ:x+3=pqu2,x2-3x+9=v2,y=uv,gcd(u,v)=1;
情形Ⅱ:x+3=u2,x2-3x+9=pqv2,y=uv,gcd(u,v)=1;
情形Ⅲ:x+3=pu2,x2-3x+9=qv2,y=uv,gcd(u,v)=1;
情形Ⅳ:x+3=qu2,x2-3x+9=pv2,y=uv,gcd(u,v)=1。
对于情形Ⅰ,由x2-3x+9=v2得x=-5,0,3,8,则有pqu2=x+3=-2,3,6,11。显然无整数解,故情形Ⅰ不成立。
对于情形Ⅱ,将x+3=u2代入x2-3x+9=pqv2,配方得
(2u2-9)2+27=pq(2v)2
(5)
对式(5)两边同取模3,得
(2u2-9)2+27≡pq(2v)2(mod 3)
因为Legendre符号

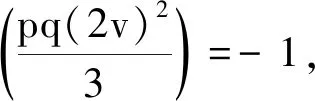
对于情形Ⅲ,将x+3=pu2代入x2-3x+9=qv2,配方得
(2pu2-9)2+27=q(2v)2
(6)
对式(6)两边同取模3,有
(2pu2-9)2+27=q(2v)2(mod 3)
因为Legendre符号
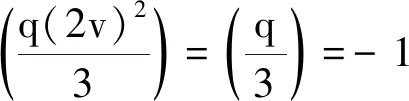
矛盾,故情形Ⅲ不成立。
对于情形Ⅳ,由u2≡0,1,4(mod 8)知,x=qu2-3≡1,2,5(mod 8),从而有pv2=x2-3x+9≡3,7(mod 8)。对于x2-3x+9=pv2,显然有v2为奇数,那么v2≡1(mod 8),则pv2=5(mod 8)。这样一来,5≡3,7(mod 8),矛盾,故情形Ⅳ不成立。
综上所述,完成了定理1的证明。
3.2 定理3的证明
类似定理1的证明方法,即可得出定理2的证明。下面证明定理3。
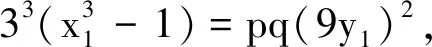
当x≢0(mod 3)时,此时有x-3≢0(mod 3)。设(x,y)是丢番图方程x3-33=pqy2的一组解,则gcd(x-3,x2+3x+9)=gcd(x-3,33)=1,故丢番图方程(4)有以下4种情形:
情形Ⅰ:x-3=pqu2,x2+3x+9=v2,y=uv,gcd(u,v)=1;
情形Ⅱ:x-3=u2,x2+3x+9=pqv2,y=uv,gcd(u,v)=1;
情形Ⅲ:x-3=pu2,x2+3x+9=qv2,y=uv,gcd(u,v)=1;
情形Ⅳ:x-3=qu2,x2+3x+9=pv2,y=uv,gcd(u,v)=1。
对于情形Ⅰ,由x2+3x+9=v2得x=-8,-3,0,5,则有pqu2=x-3=-11,-6,-3,2,显然无整数解。故情形Ⅰ不成立。
对于情形Ⅱ,由u2≡0,1,4(mod 8)知,x=u2+3≡3,4,7(mod 8),从而有pqv2=x2+3x+9≡3,5,7(mod 8)。对于x2+3x+9=pqv2,显然有v2为奇数,那么v2≡1(mod 8);又由p≡13(mod 24),q=12s2+1(s∈Z+,2⫮s),那么p≡5(mod 8),q≡5(mod 8)。则pqv2≡1(mod 8),即1≡3,5,7(mod 8),矛盾,故情形Ⅱ不成立。
对于情形Ⅲ,将x-3=pu2代入x2+3x+9=qv2,配方得
(2pu2+9)2+27=q(2v)2
(7)
对式(7)两边同取模p,有
(2pu2+9)2+27=q(2v)2(modp)
因为Legendre符号
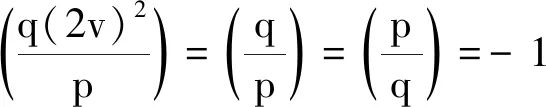
矛盾,故情形Ⅲ不成立。
对于情形Ⅳ,将x-3=qu2代入x2+3x+9=pv2,配方得
(2qu2+9)2+27=p(2v)2
(8)
对式(8)两边同取模q,有
(2qu2+9)2+27≡p(2v)2(modq)
因为Legendre符号
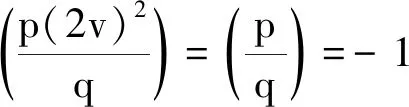
矛盾,故情形Ⅳ不成立。
综上所述,完成定理3的证明。
