线性规划法下物流运输问题的应用研究

张晶

山东畜牧兽医职业学院 山东潍坊 261061

现代企业的发展离不开物流运输，在对运输路线规划问题上，已经有多种方法并基于不同的目的进行了优化改良，本文以运输成本最小化为优化目的，使用线性规划模型，解决多供给点——多需求点的运输问题[1-3]。

1 线性规划模型介绍

线性规划模型是一种特定的约束条件下，求最值的问题，其中目标函数是线性函数，约束条件是不等式，标准式如下。

其中：X=（x1,x2,x3…xn）T为决策向量；C=（c1,c2,c3…cn）为价格向量；B=（b1,b2,b3…bn）T为资源向量。

2 线性规划模型实际应用

一种货物从m 个供给地（1，2，3…m）出发，运往n 个需求点（1，2，3…n），第i 个供给地的供给量为bi（bi∈｛1，2…m｝）第j 个需求点的需求量为di（di∈｛1，2…n｝），从i 地运往j 地的成本费用为cij。其中：

3 相关实例的具体应用

某地有3 个蔬菜物流园，向当地7 家蔬菜批发市场提供蔬菜，每日需求量、供给量以及运输成本如表1 所示。

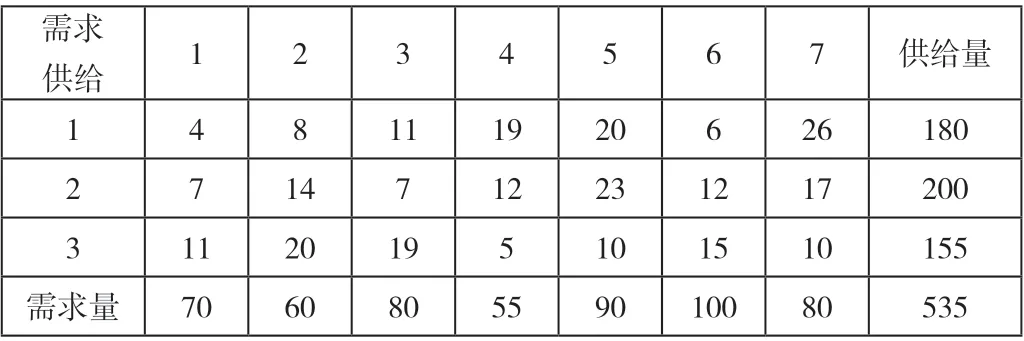
表格1 供给量、需求量及运输成本

该问题有m+n 个约束方程，在供求相等的前提下，约束方程有m+n-1 个是线性独立的，因此该问题有最优解。使用表上作业法进行求解。

（1）分别算出各行和各列最小值与次小值的差值，并写入表中的最右列和最下列，如表2 所示。

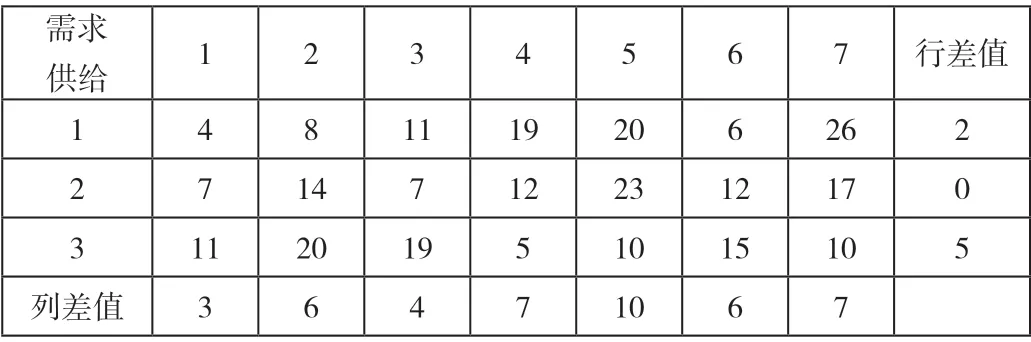
表2 成本行差值与列差值

（2）在行差值和列差值中找到最大值，选择它所在的行或者列中的最小值作为优先供应点，本例中确定供给点3 先满足需求点5，需求点5 满足后将第5 列划去，如表3 所示。

表3

（3）重复以上两步操作，直至得出最优解，如表4 所示。

表4

优化后最小运输费=20×4+50×7+60×8+80×7+55×5+90×10+100×6+70×17+10×10=4260

4 结语

对于物流运输成本问题，线性规划法条件简单，计算方便，通过建立有限制条件的数学模型，达到运费最优的优化结果，为现实中企业的生产和实践提供借鉴意义。