基于分形理论的风电功率预测算法研究
2021-04-06李昂儒郑伟彦赵京虎王辉东汪李忠邢海青
李昂儒,郑伟彦,赵京虎,杨 勇,王辉东,汪李忠,邢海青
(1.南瑞集团有限公司(国网电力科学研究院有限公司),江苏 南京 211106;2.南瑞研究院西安研发中心,陕西 西安 710000;3.国网浙江省电力有限公司杭州供电公司,浙江 杭州 310007;4.国网浙江省电力有限公司,浙江 杭州 310012;5.国网浙江杭州市余杭区供电有限公司,浙江 杭州 311100)
0 引 言
地球上的化石能源正在逐渐消耗殆尽,新能源的研发利用势在必行。其中风能资源的优点较多,比如范围广、几乎无污染、可重复利用等,俨然已成为最有潜力的新能源之一。但自然风的特点是随机性和间歇性较强[1],当大规模集中并网时,会对电网的稳定运行带来一定的威胁。准确预测未来一段时间的风电功率,对电力调度及安全运行具有重要意义。
风电功率预测常采用的方法有物理法和统计法。其中物理法不依赖风电场的历史数据[2],主要基于数值天气预报,依据风向、空气湿度、气压等作为预测模型的输入量,通过数据对风电场所在地进行建模分析,但在不同位置、不同时刻,环境因素有较大的差异,使得物理法实用性差,难推广;统计学习方法就是利用大量的历史风电发电数据、风机轮毂的风速风向、气压等数据,从大量历史数据中获取数值天气参数等输入数据与风电实际功率之间的映射规律,建立输入与输出关系,采用建立的关系模型再进行预测,常用的一般有人工神经网络(artificial neural network,ANN)和支持向量机(support vector machine,SVM)[3]等方法。
另外一种为相似日法[4],经过多年逐步的研究,已将该方法应用到风电功率预测[5]和光伏发电预测[6]中。Ashraf将神经网络、模糊推理研究和相似日法结合起来,融合相互间的优势来预测一天的风速[7];张宜阳等[8]研究者将相似日细分为“相似时段”、“基准段”和“预测段”,从不同的层次预测,却忽略了基准功率与气象特征之间的相互影响;文献[9]先采用聚类方法选取相似日,规避掉聚类的硬划分问题,但无监督方法的缺点也较明显,对原始样本要求较高且异常值敏感,容易造成分类过多,最终精度很难保障;丁志勇[10]考虑到在某段时间内风速的变化规律,提出了一种基于连续时段聚类的方法,并结合SVM算法来进行风电功率预测,但该方法难以体现历史数据与预测数据之间的相互变化关系;郑婷婷等[11]学者研究前K日功率曲线,将功率变化曲线特性考虑到模型中,但并没有分析前后相关趋势关系;王辉等[12]先进行相似日抽取,再采用主成分分析法降维,降低计算复杂度,但预测的精度不高且模型无法解释。
该文提出一种基于分形理论的混合K最近邻算法(K-nearest-neighbor,KNN)用于风电功率预测。借鉴分形理论的思想,考虑基准功率曲线问题和气象特征值,利用分形插值可有效地获取相邻样本的局部信息,再结合自定义KNN算法生成预测模型。最后基于某风电场的历史实测数据,与现有的一些预测模型进行对比验证,提出的模型预测精度有所提高,复杂度降低且性能较好。
1 分形相关定理与K近邻算法描述
1.1 分形引理
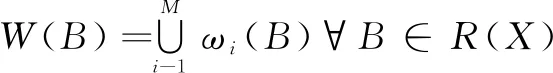

借鉴上述两个引理的思想,若将风电历史数据作为一个集合,那么就应该存在某一迭代函数系IFS,使得风力发电历史数据集合在这组映射下的象趋近于发电功率历史数据集合。
1.2 分形插值理论
该IFS[14]满足上述引理1和引理2。确定数据集{(xi,yi):i=0,1,…,M},其中的吸引子A是连续函数F:[x0,xM]→R的图像,下面构造R2上的一个IFS。
IFS{R2;ωm,m=1,2,…,M},其中ωm是式(1)的仿射变换:
(1)
其中使得bm=0是为了与小区间的函数不交叉。
每一个变换都必须满足下面的方程(2),使得在大区间的左端点和右端点可以映射到子区间的左端点和右端点:
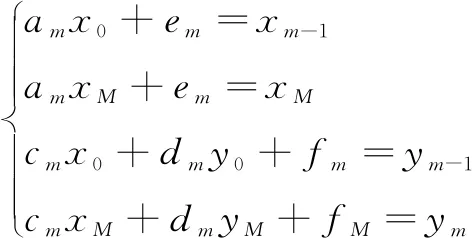
(2)
ωm的垂直比例因子为dm[15],可把自由变量选择为dm。使得dm<1,这样做使得IFS收敛。令L=xM-x0来解上面的方程组,可以得出如下方程:
(3)
IFS的第i个仿射变换可以由上式得到的参数来确定,IFS的吸引子可由IFS的各个参数求出,而稳定的插值曲线是多次迭代的结果。两个相邻已知信息点之间的局部特征在传统方法中很难反映出来,但分形插值方法有其独特的优势,可以更好地利用样本局部信息,使得原采样曲线的大部分特征得到有效的补充和保留[16]。
1.3 KNN算法描述
对于一组训练数据集合,KNN算法在训练集中寻找K个最相近实例,找出这K个实例后将其作为候选类。再以之间的相似度作为权重,代入预先设置好的阈值,就基本可以确定该样本的分类[17]。
一般情况下,某一时间的风电功率数值可能与其时间点最近邻的m个的风电功率数值最为相似。用m长度的时间序列β0={αn-m+1,αn-m+2,…,αn-1,αn}来预测αn+1。先确定β0的K个最近邻,在{α1,α2,…,αn}的已知时间序列中,以β0为基础时间序列,逐步移动窗口,取(n-m)个长度为m的子序列,再找出β0的K个最近邻,用两向量的夹角余弦值来表示相似度,如下:
其中,βij表示向量βi的第j个分量。由此可知,余弦值越大的话,相似度就越大[18]。最后,将这K个向量最后一个分量之后的近邻元素视为αn+1的一个最近邻。如此就得到αn+1的K个最近邻b1,b2,…,bk,再对K个数加权平均即可求得αn+1。
2 基于分形理论的混合KNN算法预测模型
风力发电时间序列有周期性特征,日发电曲线在时间尺度上具有自相似性,也存在非常相近的分形维[19],一段发电时间序列也同样具有相关性。可以将历史数据和发电曲线拟合成一个相似的周期,借鉴分形插值法可以很好地利用相邻已知点的局部信息的特点[16],使算法快速地收敛于真实值。传统KNN算法中每次需要对历史样本集进行搜索以获取n个相似历史样本集[20],当设定的K值增大时,搜索次数不断增加,搜索的重复样本不断出现,不仅消耗额外的存储空间,还会大大降低系统的运行速度。
为弥补传统算法的一些缺点,该文设计了基于分形理论的混合自定义KNN算法。该算法基于分形理论中的自相似性的分形维,再结合KNN算法的相关理论,对搜索相似历史样本集的方式进行改进,既减少了消耗的内存空间,又降低了算法的时间复杂度。
预测模型的主要流程如下:
(1)将预测日设为起点,用于分割分形维数据,其中一部分用于训练,一部分用于验证。
(2)将横轴作为分形维点集合的时间坐标,然后分析基准日的功率曲线特征,找出曲线的主要特征点。在本例中主要考虑天气因素中温度、风速、风向这三个主要特征,选定九个整点的功率值。
(3)建立基准日的功率曲线IFS。迭代函数系统通过第(2)步的插值点集合来建立,可以知道dm取0.9~0.95时,预测误差最小,用来计算的公式为式(3)。
(4)建立功率曲线IFS。插值点的集合通过第(2)步的基准时间坐标和每个相似的各个点所对应的功率值得到。迭代函数分别建立,其中d值保持不变。
(5)计算结束后,将风速、风向、温度这三个主要特征的分形维保存到内存中,KNN算法不再搜索所有的历史样本集,而是从主要特征的分形维去搜索,大大减少了算法的搜索量。
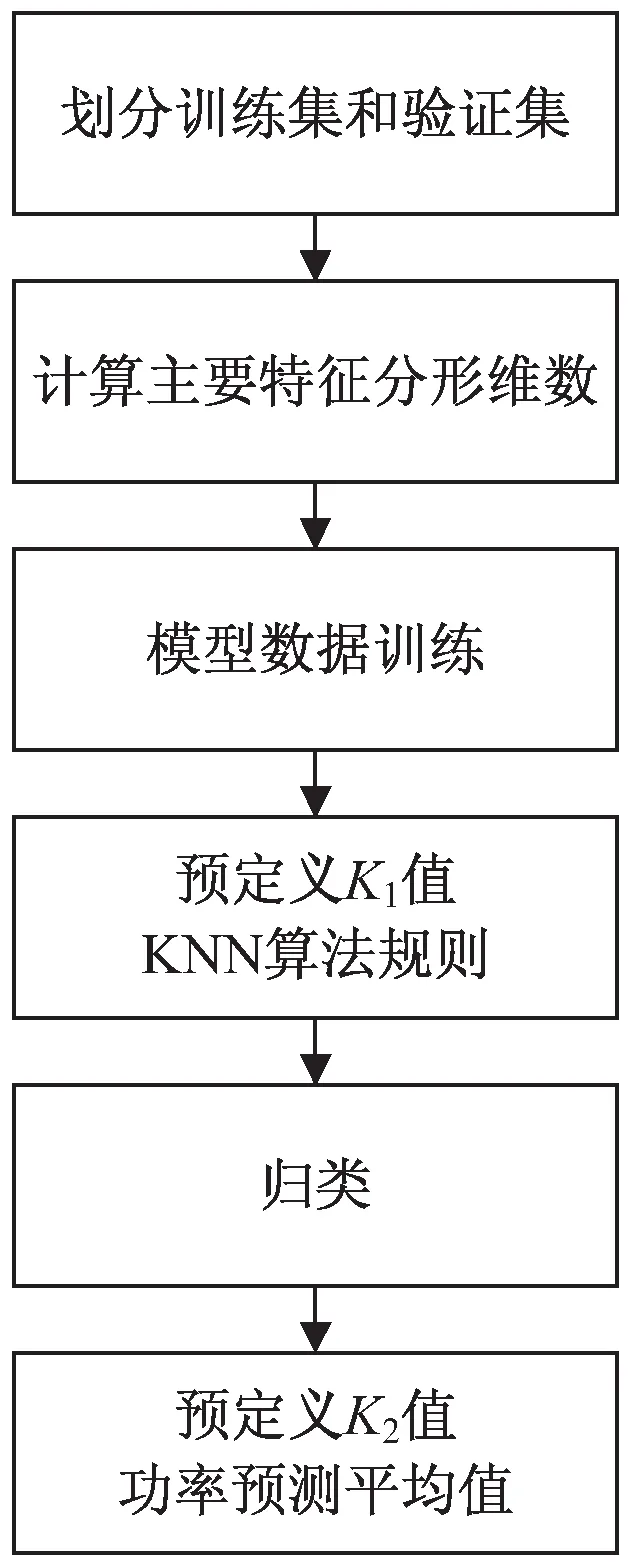
图1 风电功率短期预测模型框架
(6)根据当前数据集中指定的测试集日期,找出最近的9个时间点的观测值组合成数据帧(DataFrame1),计算这个数据帧中风速、风向、温度三个特征的分形维数;(a)根据权重值和K1值,通过计算欧氏距离去找到K1个最近邻的时间范围内的分形维缓存值,根据缓存值找到相应指定日期,再根据指定日期将原始数据中天气观测值和训练集中的功率值组成一个新的数据帧(DataFrame2)。(b)输入DataFrame2和测试集中天气观测值参数,根据权重值和K2值,通过计算欧氏距离找到K2个最近的预测功率值,将K2个值做加权平均后作为最终的预测功率值。基于分形理论的混合KNN算法预测模型如图1所示。
3 算例分析
以某风电场(20台机组)为例,选取该风电场自2019年1月1日至2019年12月1日共334天的数据作为样本数据,将前290天数据作为训练样本集,利用该训练样本集预测后44天的测试对象集。设置预测的时间间隔为15分钟,提前24小时进行预测,计算出各个预测时间点在后44天内的功率平均值,并与后44天的实际功率值进行比较。同时与随机森林模型(random forest,RFR)、支持向量机模型(SVM)、梯度提升决策树模型(gradient boosting decision tree,GBDT)进行对比,计算各算法的均方根误差(root mean square error,RMSE)和预测准确率,来验证提出的基于分形理论的混合KNN算法预测模型是否具有更高的准确性和有效性。
在基于分形理论的混合KNN算法预测模型中,该文设置了两次K值,第一次K值为3,主要是为找到最近邻的时间范围内的分形维缓存值,第二次K值为5,主要是为找到最近的加权平均功率值,对测试时间点进行预测,然后对实际功率和预测功率进行对比。结果如图2所示,横坐标为预测时间轴,纵坐标为功率值。

图2 基于分形理论的混合KNN算法模型的 预测功率与实际功率对比
RFR模型的预测功率曲线如图3所示,通过随机搜索法结合网格全局搜索最优参数调参,确定n_estimators=100,max_depth=10;SVM中的核技巧采用Linear核函数,degree=3,采用惩罚系数调整模型,防止过拟合,最终预测功率曲线如图4所示;GBDT模型的预测功率曲线如图5所示,通过超参数调参,不断修正模型,确定learning_rate=0.1,n_estimators=500,max_depth=3。

图3 基于随机森林算法模型的预测 功率与实际功率对比

图4 基于支持向量机算法模型的预测 功率与实际功率对比

图5 基于梯度提升回归算法模型的预测 功率与实际功率对比
四种模型在超参数调优后,预测模型的均方根误差(RMSE)、训练模型数据消耗的时间(CT)、模型拟合优度(SCORE)如表1所示。

表1 不同预测模型下风电功率预测对比
从表中可以看出,SVM预测模型的表现最差,将低维数据映射到高维空间中,模型训练消耗的时间也较长,同时RMSE并没有减小;GBDT经过不断的超参数调优后,模型训练消耗的时间有所减少,但RMSE和模型拟合度值的提升幅度并不明显;RFR预测模型在一系列调整超参数后,模型拟合优度提升明显,但同时模型训练时间有所增加;而提出的基于分形理论的混合KNN风电功率预测模型不论在均方根误差、模型拟合优度还是训练消耗时间上都有更好的表现,充分验证了该模型可以很好地用来预测风力发电功率。
4 结束语
风电作为最具潜力的新能源之一,目前的并网容量仍在不断增加,大规模的风电并网时对电网运行冲击很大,为应对风电强随机性带来的挑战,风电功率预测的准确性提升得到极大关注。该文所作的一系列研究,目的就是为提升风电预测精度,将分形思想相关理论与自定义的KNN算法相结合,先对样本中的几个重要特征进行分形维数计算并插值后存储于内存中,再结合KNN算法进行两次搜索,一次是最近邻的时间范围内的分形维数缓存,另一次是找出最近邻的加权平均功率值。同时,与现有的风电功率预测方法进行对比,在各指标上都有更好的表现。该方法引入分形思想可以较好地保证样本的局部信息,模型简单,复杂度低,特别是针对大数量的样本,算法性能依然良好。具体分形维数最优值的选取上仍需要进一步研究,这也将是后续研究的主要方向。
