基于非均匀热扩散的交互式图像分割算法

孙凯月，刘向阳

(河海大学 理学院，江苏 南京 211100)

0 引 言

图像分割是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程。图像分割在很多领域有着广泛应用，如医学、军事、气象等。根据在分割过程中是否有用户的参与，可以将图像分割划分为自动式图像分割和交互式图像分割，该文主要研究交互式图像分割。交互式图像分割之初，需要用户的交互操作指定限制条件，指导分割，分割完成后也可添加新的限制条件得到所需前景或背景结果。

比较经典的交互式图像分割算法有基于Graph Cuts的算法[1-3]、基于透明度的算法[4]、随机游走算法[5-6]、深度学习算法[7-9]和测地算法[10-12]等。Graph Cuts的基本思想是通过构造图，使用最大流最小割集定理获得某种特定形式的能量函数的全局最优解。基于透明度的方法[4]可以对单个像素点包含的色彩进行前景和背景的分离，由于算法中加入了透明度，提取的结果中允许存在羽化的边缘。随机游走算法[4]通过对像素点贴标签，计算任一点随机到达背景或前景的概率，从而决定指派区域。深度学习算法的核心思路是通过卷积神经网络(CNN)自动获取分割。2018年，Wang等人[10]用测地线距离图将用户与CNN的交互结合起来，并提出了一种能够给出更好的密集预测的分辨率保持网络。

除此以外，还有许多其他基于精确测地距离计算的图像分割算法。2008年Criminisi等人[11]将图像分割问题转化为近似能量最小化问题，提出了一种基于测地距离的并行滤波算子用于获取空间光滑、对比度敏感的分割。2012年Wei等人[12]利用背景的边界和连通性，提出了新的测地特征度量。在该类算法中，有效的测地距离计算方法始终是保证精确分割的前提。Fast Marching算法是计算测地距离的精确算法，2000年由Sethian等人[13]提出，主要思想是通过求Eikonal方程的数值解，近似测地距离。2013年Crane等人[14]探寻热与测地距离之间的关系，提出了热方法(heat method)，核心是由热方程找到距离增加的方向，再还原测地距离。

该文基于热方法，提出了一种非均匀扩散的热方法计算测地距离，并将其应用于交互式图像分割。图像的颜色信息可用于构造三角网格，作为热扩散的媒介。此外，通过引入热扩散系数，热方程被推广到了更一般的形式，即非均匀的热流方程。由于热的梯度与距离梯度平行，用热扩散计算得到的单位梯度场，可用于还原真正的测地距离函数。最后，设置测地距离分割限制条件，即可快速有效地实现图像前景分割。

1 热方法

1.1 程函方程(Eikonal)

过去几十年中，许多距离的逼近算法[15]都是基于求解Eikonal方程：

(1)

满足边界条件φ|γ=0，γ是边界，可以是一个点或者一条曲线，φ是距离函数。Eikonal方程是非线性的双曲方程，很难直接求解。Fast Marching算法利用一阶逆风差分格式求得数值解，近似测地距离。算法中使用了优先队列，靠近源点处的测地距离可以很快计算出来，但并行化问题无法解决。该方法最大的弊端在于，它们都没有重用信息，对于不同的源点，两点间的距离需要整个重新计算。虽然热方法和Fast Marching都是基于Eikonal方程，但Fast Marching算法属于波传播的模型，而热方法探寻的是热与距离之间的关系，鲁棒性强，精度高，更易于操作，且预计算中的大量信息可以被重用。

1.2 主要思想

由于观察到热扩散的梯度与真正的距离函数的梯度平行，方向相反，所以热方法首先需要找到距离增加的方向，然后利用泊松方程还原测地距离。热方法可以应用于任何定义了梯度算子、散度算子以及拉普拉斯算子Δ的连续空间，主要包括以下步骤[14,16]：

(2)计算单位向量场X=-ut/|ut|；

(3)解泊松方程Δφ=·X。

给定源点集，当t→0，函数φ近似于真正的测地距离。热方法还可以应用于任何维度，以及定义了梯度和内积的任何域，包括正交网格、三角网格和点云，这里着重讨论三角网格上的热扩散。

1.3 拉普拉斯和梯度

为了将连续的过程转变为离散的算法，核心是对梯度和拉普拉斯算子进行空间上的离散化。给定三角网格，V表示顶点，E表示边，F表示面片，则点i处的拉普拉斯离散化公式为[14,16]：

(2)

其中，Ai是i点附近所有三角形面积之和的三分之一，j是i的邻近点，αij,βij是对应边的两个对角。

梯度的离散化公式为：

(3)

其中,Af是三角形面片f的面积，N是向外的单位法向量，ei是i的边缘向量，ui是其对角i的u值。

2 基于非均匀热扩散的交互式图像分割算法

2.1 非均匀热扩散

将热方法中的热方程推广到更一般的形式：

(4)

其中，D是热扩散系数，γ是源点或一条曲线，δ是指示函数。在均匀的各向同性介质中，D通常表示为一个常数标量乘以Id，标量代表传导率，Id是单位矩阵。如果各个区域上的传导率不同，则可表示更一般介质上的非均匀扩散[17]。

假设p是图像上的任意像素点，可以定义热扩散系数D为：

(5)

其中，Q表示人工交互区域，f是图像的灰度值或RGB函数，q>1用于调节交互区域上的扩散速度。于是，非均匀热方程在三角网格上可以离散化为：

(6)

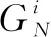
2.2 单位向量场

由于热扩散的方向平行于真正的距离增加的方向，故可用非均匀热流方程解的梯度近似最终的距离函数梯度，从而还原测地距离。热流梯度的大小可以忽略，这里，由Eikonal方程，假设距离函数的梯度是单位长度的。另外需要注意的是，热增加的方向与距离增加的方向相反，故还需对其进行负化得到下面的单位向量场：

(7)

2.3 泊松方程

利用单位向量场，最终的测地距离函数φ可通过求解下面的泊松方程还原。

div(Dφ)=·X.

(8)

令b为单位向量场的散度向量，泊松方程可以离散化为三角网格上的稀疏线性方程组：

(9)

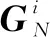
2.4 交互式图像分割算法

原理：非均匀扩散的热方法计算得到的测地距离可用于分割图像的前景或背景区域。这里，主要讨论前景分割。如图1所示，假设图像的前景区域由三个灰度值不同的矩形组成，若选定第一个矩形中某一点为源点，计算测地距离并设置限制，只能将前景中最上方的矩形分割出来，图1(a)中的黑边框即为分割的边界线。而经过图1(b)中的人工干预，标记区域上的热扩散速度增加，使得灰度值不同的三个部分之间测地距离变小，消除了内部边界，从而分割出完整的前景部分。这里，将人工干预区域始末两点设置为源点。

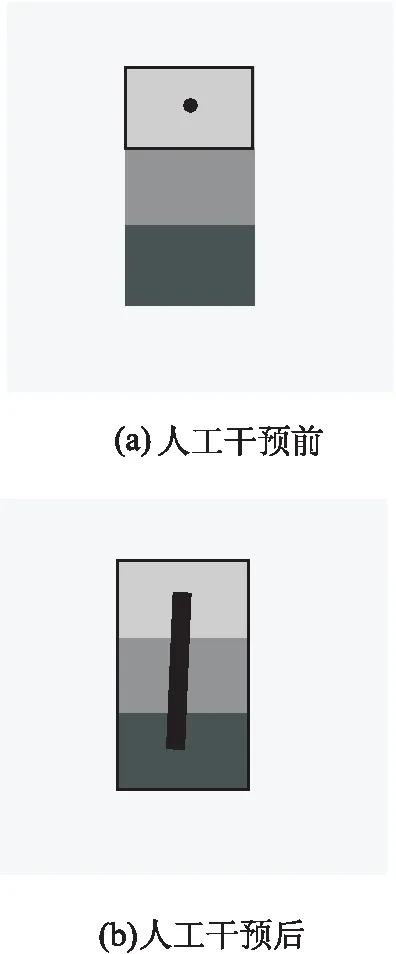
图1 人工交互对分割的影响

如下面的西瓜示例中，图2中的(b)、(c)分别是人工交互前和人工交互后的测地距离等值线图和分割结果图。前者以半个西瓜上某一点为源点，只能分割出前景的一部分。后者将人工标记区域上的热流扩散速度设置为q=200，则前景中两个不同部分之间的测地距离变小，边界消除，最终分割出了完整的前景区域。

图2 人工交互下的前景分割示例

该算法的核心思路是通过非均匀的热扩散计算测地距离，从而实现交互式图像分割。图像的灰度值或RGB值可用于构造Delaunay三角网格，作为热扩散的媒介。值得注意的是，梯度更大的边界会导致其周围两侧点之间的高度相差更多，热流扩散得更慢。非人工区域上的热扩散系数中，设置梯度与扩散速度呈反比，同样减缓了热在边界上的扩散。经过人工交互，更多的测地距离等值线密集在外部边界上，形成了完整的前景轮廓。最后，只需设置相关的分割限制条件，即可分割出感兴趣的前景区域。该算法步骤简单，操作方便，预计算中大量信息可以重用，节省了内存和时间消耗，整体流程如图3所示。

图3 基于非均匀热扩散的交互式图像分割算法流程

3 实验结果和分析

3.1 参数评估

图4是一幅灰度值相同的二维图像，图中的曲线是人工交互标记部分。以“×”为源点，不同扩散速度的热方法下的测地距离计算结果存在明显差异。

图4 人工干预

图5分别是设置q=40，q=100，q=200，求解方程(4)得到的热扩散图。随着扩散系数q不断增大，更多的热扩散到了人工标记的区域上。

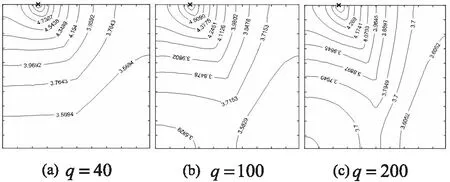
图5 不同扩散速度下热方程的解

图6是由式(7)计算得到的单位向量场，其中ut是非均匀热方程(6)的数值解，热扩散系数(5)中分别设置：q=40，q=100，q=200。随着人工标记区域上的热扩散速度不断增加，其周围的向量偏离标记曲线指向两边外侧的幅度越大。单位向量场指向的是测地距离增加最快的方向，这可以近似看作源点集由原先的一个点不断向一条曲线演变。

图6 不同扩散速度下的单位梯度场

图7是由泊松方程(9)计算得到的测地距离图，人工标记区域上的热扩散系数设置同样的值。随着q不断增加，标记曲线上的测地距离也不断减小。

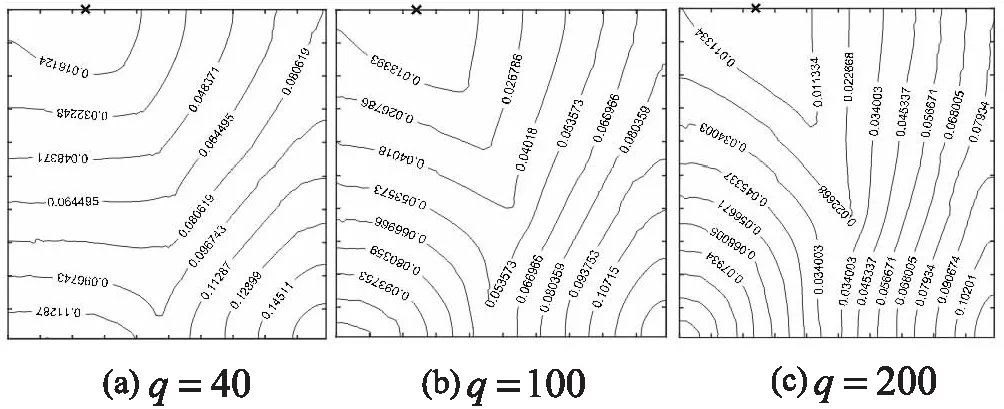
图7 不同扩散速度下计算的测地距离

3.2 实验结果及分析

基于非均匀热扩散的交互式图像分割算法可以应用于各类真实图像中复杂前景的提取，包括人物、动物、建筑等等。图8中的(a)为人工标记的图像，(b)是由非均匀扩散的热方法计算得到的测地距离图，设置q=200，(c)是最终的分割结果。(b)中可以看到，更多的距离等值线密集在前景的外部边界上，形成了明显的轮廓，这时，只需要设置像素点的距离小于轮廓处的距离值就可以将前景完整地分割出来。值得一提的是，尽管图8中的前景和背景都较为复杂，但该算法也只需要一笔少量的人工标记就可以实现有效的分割。

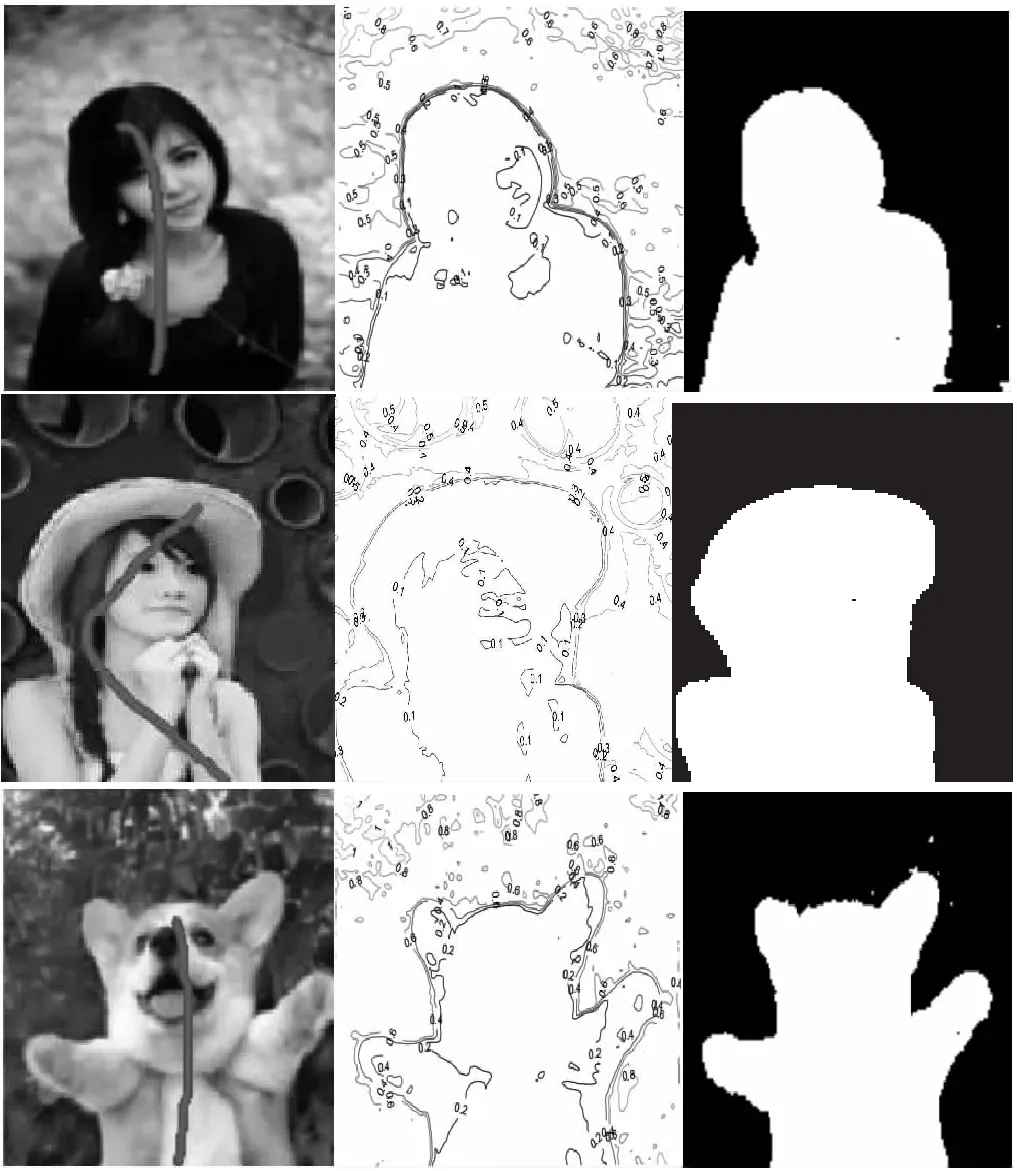
图8 非均匀热扩散的交互式分割算法应用于各类图像

4 结束语

提出了一种非均匀扩散的热方法计算测地距离，并将其应用于交互式图像分割。基于热方法，算法中引入并定义了热扩散系数，将热方程推广到了更一般的形式。非均匀扩散的热方法计算测地距离仅需求解两个稀疏线性方程组，简单快速，更易于操作。实验结果表明，该算法可以精确有效地应用于各类真实图像的交互式分割，且无需过多的人工干预。在得到测地距离之后，分割限制条件的设置还有待进一步的调整，以便适用于更加复杂的现实图像。如何有效且充分地综合利用好图像的颜色和纹理信息也是接下来优化算法的努力方向。