基于小波非线性自回归网络的水文预测模型

衣学军，魏守科，石玉好，付常璐，邢昱臻，闫 杰，赵金东

(1.烟台市水文局，山东 烟台 264000；2.烟台大学 计算机与控制工程学院，山东 烟台 264005；3.山东琢瑜清泉智能软件科技有限公司，山东 烟台 264000；4.北京迪普讯智能信息技术有限公司，北京 100089)

0 引 言

不同时间尺度(年、月、日、小时等)上的水文序列预测在水资源合理调配和防洪减灾决策中起着至关重要的作用。随着机器学习算法的发展，人工神经网络(artificial neural network，ANN)被应用于包括水质、水流量和洪水预测在内的各个领域[1-2]。ANN是一个强大的函数逼近器，非常适合预测非线性水文时间序列，与传统ARMA、概念模型和物理模型等方法[3-4]比较具有良好的预测性能[5]。然而，当序列具有高度非线性、非平稳性且噪声过多等特征时，单一的ANN通常难以准确捕捉其变化趋势[5]。

小波变换能够同时揭示序列信号内的频谱和时间信息，其与ANN结合的方法来预测水文时间序列的研究[6-8]显示能显著提高神经网络的预测能力、预测精度，并延长了预测时间。近几年，小波分解与深度学习网络结合的方法在水文序列预测中也得到一定的研究[9-10]。

该文提出了基于小波变换非线性自回归神经网络模型(WNARN)的水文时间序列预测方法，并与单一的NARN模拟结果进行对比，验证所提出方法的精确性和有效性。

1 主要方法

1.1 小波分析

小波分析(WA)与传统的傅里叶分析(FA)相比具有许多优势。它允许将较长时间间隔用于低频信息，而将较短的区域用于高频信息。小波变换(WT)主要有两种方法：连续小波变换(CWT)和离散小波变换(DWT)。CWT由以下公式定义：

(1)

(2)

其中，Wf(a,τ)为小波系数，t为时间间隔；f(t)为输入信号；ψ(t)为母小波函数；ψ*(t)为ψ(t)复共轭函数；a为尺度因子或频率因子，可将母小波拉伸或压缩到某一频率；τ为时间因子或平移因子，作用为将母小波平移到某一时域。

CWT分解时会产生大量冗余数据，实践中通常使用DWT。如果定义：

k=0,1,…,m∈Z

(3)

其中，(ψa,τ(t))可表达为：

(4)

因此，离散小波变换可以表示为：

(5)

DWT常采用二进小波作为小波变换函数，即让a0=2,τ0=1，离散小波变换变为：

(6)

Wf(a,τ)和Wf(j,k)可以在频率(a或j)和时域(τ或k)上反映原始序列的特征。当a或j较小时，频率分辨率很低，而时域很高；当a或j变大时，频率分辨率高，但时域较低。因为离散时间序列信号f(t)时间步长t为离散整数，所以二元离散小波变换可以写成：

(7)

输入信号用以下公式重构:

(8)

式中小波系数Wf(j,k)通过低通滤波器l(ψi,k(t))被分解为分近似层(或低频)系数(cAn)，通过高通滤波器h(ψi,k(t))分解为不同细节(或高频)(cD1，cD2，…，cDn)层系数(图1(a))。cAn提供有关原始信号的近似信息，而细节层系数包含有关原始信号的详细信息，如周期、中断、跳变等。原始信号可以表示为：

(9)

或简化为：

f(t)=An(t) + ∑Dn(t)

(10)

其中，An(t) 是小波分解第n层近似系数值，Dn(t)是小波分解后细节各层的系数值。

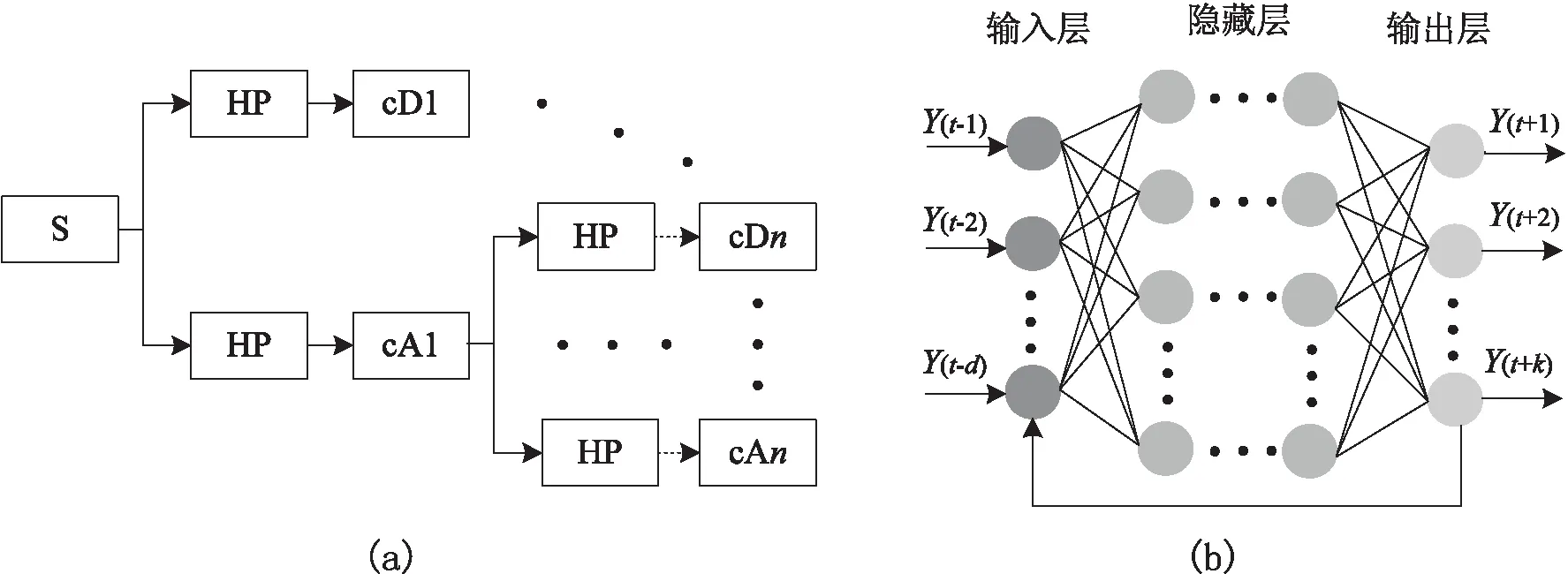
图1 小波分解原理和BP算法的非线性自回归网络

1.2 非线性自回归网络

人工神经网络(ANN)靠大量人工神经元(单元，细胞或节点)联结进行计算，具有强大的函数逼近能力。最常见的网络结构是多层前馈静态神经网络(MLFN)。非线性自回归网络(NARN)是一种动态神经网络，适合时间序列预测,已在一些领域得到了研究和运用[11-13]。序列Y(t)的未来值由该序列过去的d个值决定，其表达式为：

Y(t)=f(Y(t-1),Y(t-2),…,Y(t-d))

(11)

标准的NARN是前馈网络，隐藏层传递函数为sigmoid，输出层为线性传递函数。该文使用误差反向传播算法(BP)使得每个误差信号都可以从输出反向传播到输入层以调整权重(图1(b))。

2 WNARN模型

2.1 模型框架

WNARN模型主要技术流程包括：(1)数据预处理；(2)将处理好的数据进行分解；(3)分解后的子序列作为模型的输入向量；(4)模型的训练和测试；(5)模型结果评估；(a)如果评估结果达到目标要求，进行数据后处理，如反归一化等；小波重构原始系列的预测值；(b)如果评估结果达不到目标要求，返回前面步骤进行错误检查(见图2)。

2.2 模型实验环境

实验所使用的计算机配置为：处理器Intel(R) Core(TM) i5-8250U，CPU频率1.60 GHz，内存8 GB，操作系统Windows 10 (64位)。程序设计语言为MATLAB 2012b，小波分解和重构运用MATLAB Wavelet ToolboxTM4.1工具包，模型搭建、训练和测试运用MATLAB Neural Network ToolboxTM8工具包。

2.3 数据预处理

试验数据无异常值和缺失值，所以只需要把数据归一化将数据集转换，确保所有变量都受到同等关注，并提高训练网络的效率。该文使用贝叶斯正则化法(BR)优化网络，当数据在范围[-1，1]时，BR算法效果通常最佳[5]。利用Matlab的mapminmax归一化方法将试验样本归一到[-1，1]，其计算方法如公式(12)所示。

(12)

其中，Ynorm为归一化后的值；Ymax、Ymin分别为目标值的最大值、最小值；X、Xmax、Xmin分别为输入值、最大值、最小值。如果某输入数据全部相同，即Xmax=Xmin，除数为0，此时数据不变。

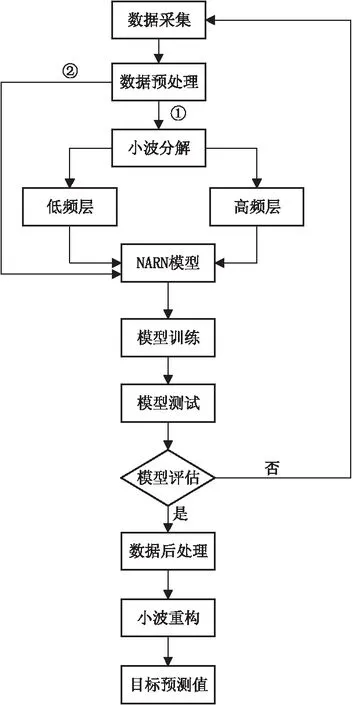
图2 WNARN模型技术框架

2.4 小波的选择

母小波类型和分解层数的选择是小波分析中的两个重要问题。该文选择Daubechies 5(db5)分解实验序列，其原因在于：(1)db小波是最广泛使用的小波族之一；(2)db较适合相对平稳的序列；(3)db5又是db小波族中最常用的小波之一，适合比较平滑的数据集[5]。根据文献[14]，小波最大分解层数可以利用式(13)计算，但同时应短于测试数据长度[15]。

Lmax=log2(nd/(lw-1))

(13)

其中，Lmax为小波可分解的最大层数；nd为序列的长度；lw为滤波器的长度。

2.5 网络训练

运用三层网络结构(p,d,m,n)来训练模型，其中p是输入向量，d是反馈延迟(Lag)，m是隐藏层神经元，n是输出向量。网络训练过程从1个神经元(m=1)和1反馈延迟(d=1)开始。如果经过50次训练网络性能无法改善，则逐渐增加神经元数目和反馈延迟。此过程持续进行，直到延迟数和评估指标R、RMSE、MAE和MARE等达到最佳为止。

2.6 过拟合问题

提前停止训练(early stopping)和正则化(regularization)是提高神经网络泛化能力，解决过拟合问题的两种常用方法。数据集较小时，正则化法则提供比提前停止训练更好的泛化能力[5]，其主要原因在于正则化不需要把训练数据集再次划分出验证数据集，进而可以充分利用所有训练数据。正则化方法通常用式(14)和式(15)表示。

msereg=γmse+(1-γ)msw

(14)

(15)

其中，msereg为正则化MSE，γ是性能比，w和msw分别为MSE的权重和平均值。在Matlab中，直接调用trainbr函数便可以在网络训练中实现贝叶斯正则化法自动确定最佳参数来改善网络泛化能力。

2.7 延迟的显著性

时间延迟(Lag)显著性是判断NARN模型有效性的一个重要指标，其主要通过检查误差自相关函数(EACF)和输入-误差互相关函数(IECF)的显著性来评估。EACF描述了模型误差其自身在不同时间点的互相关性，IECF显示输入序列与模型误差两者之间的互相关性。对于一个理想的预测模型，自相关函数应只有一个非零值，而所有输入-误差互相关函数值应均为零。

2.8 模型评价指标

选择以下评价指标对模型拟合和预测能力进行评估，分别为相关系数(R)、均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对相对误差(MARE)，其计算公式如式(16)～式(19)。此外，运用最大绝对相对误差(AREmax)和最小绝对相对误差(AREmin)评估预测结果的最大错误和最精确点，运用最大观测值预测结果的绝对相对误差(AREmaxy)和最小观测值预测结果的绝对相对误差(AREmaxy)评估模型对水文序列极大极小值(如洪水和干旱事件)预测的准确性[5]，其计算公式如式(20)～式(23)。

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

3 实验结果与分析

3.1 实验数据

运用渭河华县、咸阳和临潼3个水文站的水流量序列数据来训练和测试模型。华县和咸阳数据为1960年1月至2001年12月42年504个月水流量序列，临潼为1961年1月至2001年12月492个月的水流量序列。3个系列后48个月(4年)的数据集(约10%)用于模型预测能力测试，其余数据用于模型训练。表1统计分析结果显示训练集均值、标准差、偏度和峰度均大于测试集的相应值，这会导致单一ANN预测结果精度偏低。

表1 实验数据训练和测试集划分及统计分析

3.2 小波分解结果

测试数据为48个月，按照离散小波分解运用2的整数次幂的二进制法，即21-22-23-24-25，最多分解为5层。如果分解为6层，则26为64，测试数据集没有足够的长度。

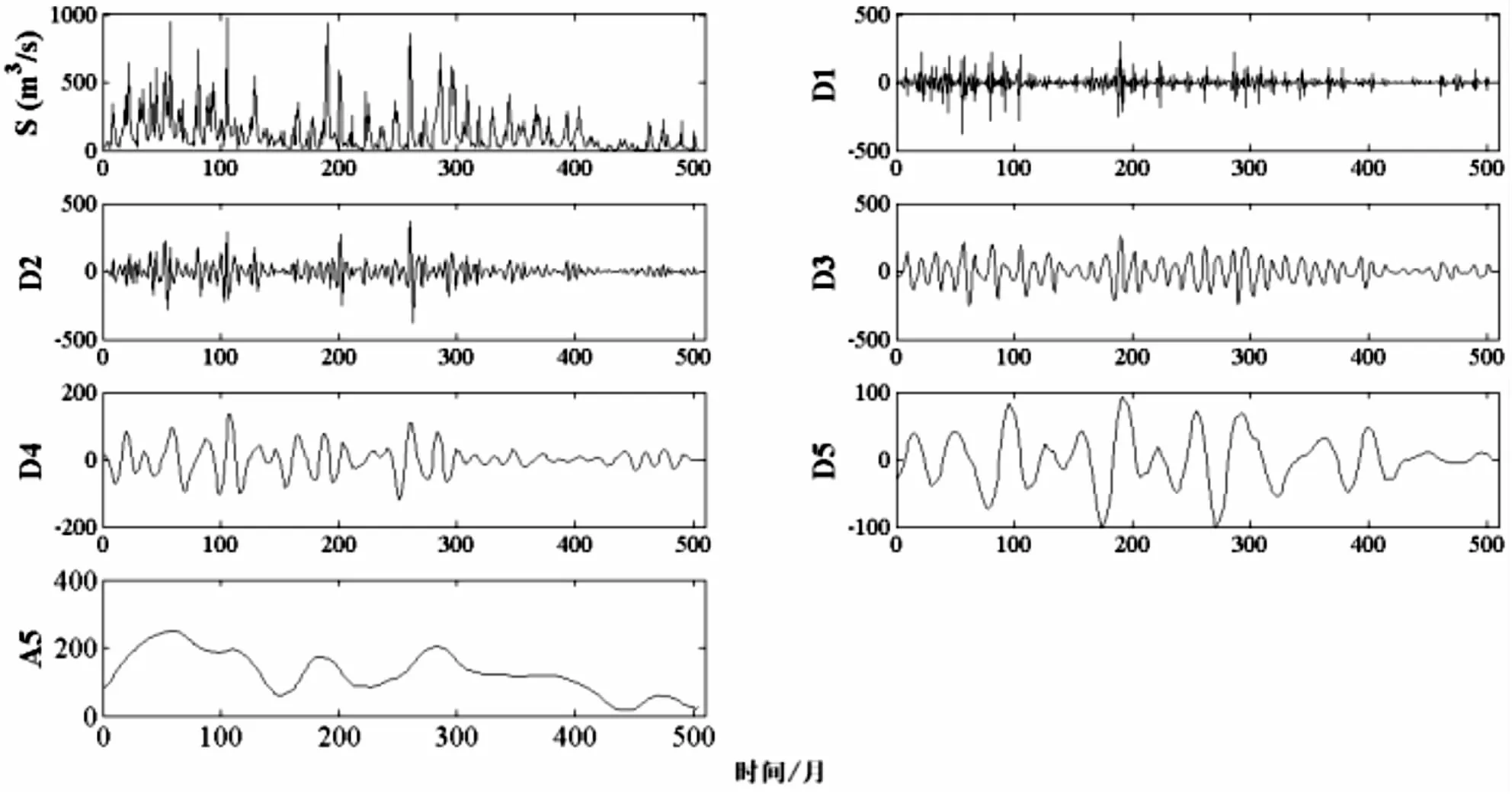
图3 咸阳站水流量序列db5小波分解为5层的结果

分解后低频层代表了序列的长期趋势，各细节层代表了不同时域上的频率变化。如图3所示，db5小波把咸阳水文站水流量序列分解为5层1个低频和5个高频层子序列。高频层显示了此序列不同时间尺度上的波动频率，如2个月模式(D1)、4个月模式(D2)、8个月模式(D3)、16个月模式(D4)和32个月模式(D5)；低频层(A5)则显示了此水文序列在500个月上的变化模式，即150个月左右上由1个大的上升下降波动，然后经过几个较小循环波动，呈逐步下降的趋势。

3.3 延迟的显著性判断

图4显示了咸阳站水流量序列模型的误差自相关函数(EACF)和输入-误差互相关函数(IECF)曲线。WNARN在隐藏层中使用了反馈延迟(lag)3(d=3)和10个神经元(m=10)之后，除了滞后为零外，EACF几乎均落入零附近95%置信范围内(图4(a))，而IECF的值也均落在零附近置信范围内(图4(b))，说明WNARN是有效的。

图4 咸阳水文站序列模型的时间延迟显著性

在相同网络结构(d=3，m=10，n=1)下，单一的NARN1在滞后±12处存在误差自相关(图4(c))，且在滞后±10，±11和±12时输入-误差相关性很大(图4(d))，时间延迟并不显著，单一的NARN1模型无效。通过增加隐藏层中神经元数目至13(m=13)改进的NARN2模型的EACF和IECF曲线都落在零附近的置信范围内(图4(e)、图4(f))；但对于数据较小时13个神经元相对较多，可能会导致网络的不稳定性。

3.4 训练结果

训练结果显示，WNARN模型相关系数R均约为0.99；而NARN1的R却在0.6左右，改进的NARN2的R值有所提高，但仍在0.93以下(见表2)。这表明WNARN模型拟合结果远优于NARN。

拟合值(Output)和目标值(Target)相关图更直观显示两模型优劣。以临潼站为例，图5(a)显示WNARN模型输出值和目标值的相关曲线与图形中45度线几乎重合，表明模型达到最佳拟合。然而，两个单一NARN模型相关曲线与45度线偏离极大，表明NARN模型拟合度欠佳(图5(c)、图5(e))。

此外，在网络结构(d=3，m=10，n=1)下，WNARN模型在其他各评估指标上也均达到最佳拟合性能，RMSE、MAE和MARE分别为0.038～0.047、0.029～0.035和0.054～0.079(见表2)。相比之下，单一的NAR1模型误差却相对较大。改进的NARN2模型虽然显著缩小了对应的误差项，提高了模拟精度，但与WNARN相比，NARN拟合精度仍然欠佳。

表2 WNARN和NARN模型训练和测试评估结果

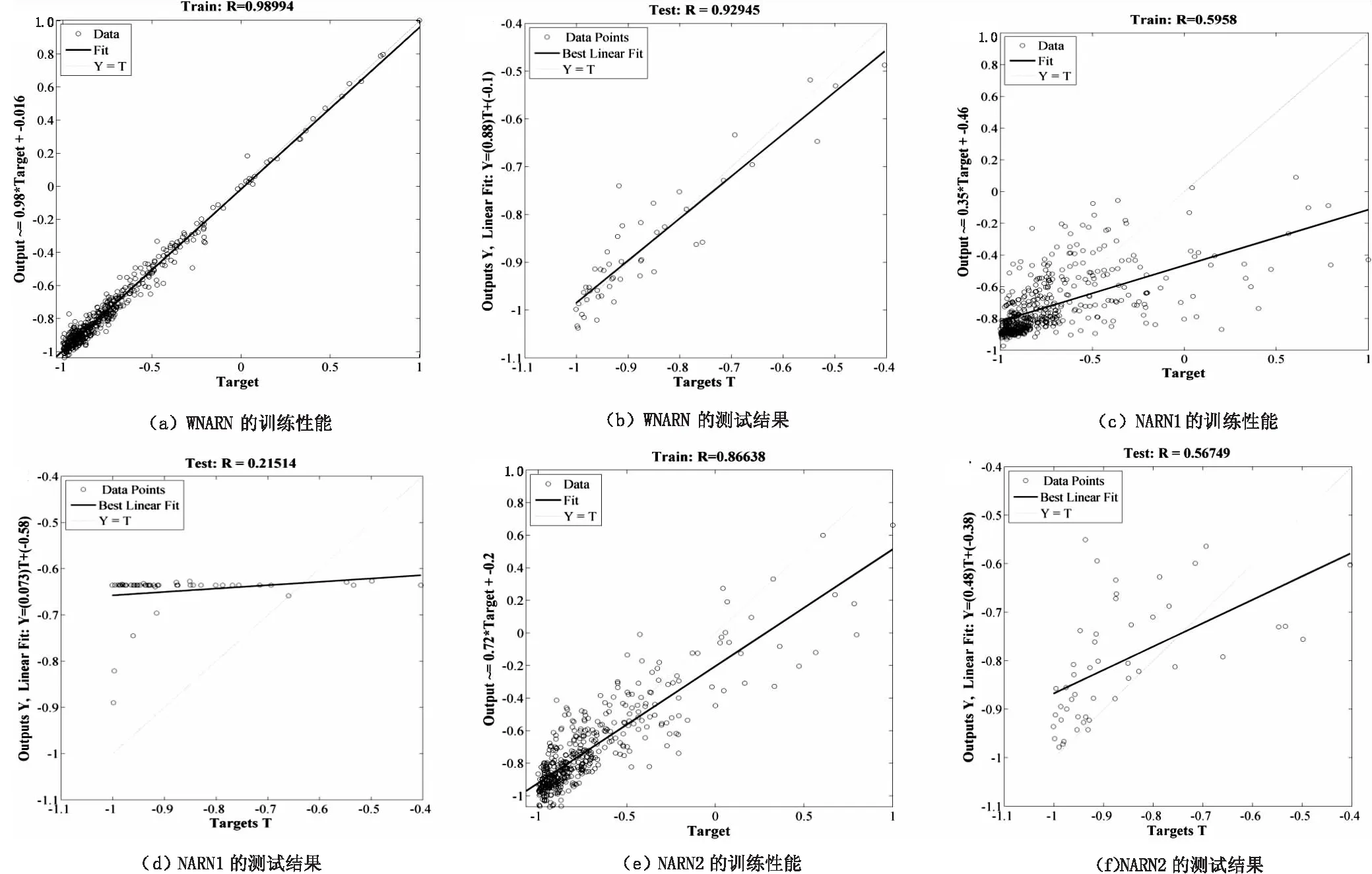
图5 显示以目标为单位的网络输出的回归图(以咸阳出水口为例)

3.5 测试结果

WNARN和NARN模型向前48个月预测结果显示，WNARN相关系数R达到了0.912～0.929；而NARN1的R仅为0.117～0.215，改进的NARN2模型R值有所改善，但仍在0.57以下(见表2)。

预测结果与目标值的相关图进一步显示两模型的预测性能，以临潼序列模型为例，图5(b)显示WNARN模型输出值和目标值比较靠近图形45度线，表明此模型预测输出与目标极为接近，预测能力较高；而两个单一NARN结果极大偏离45度线，表明其预测能力较差(图5(d)、图5(f))。尽管增加隐藏层神经元个数改进后的NARN2模型在训练结果的R值相对较高，但其预测结果R却极低，表明NARN2虽然可以较好拟合历史数据，却缺乏预测能力。

从其他评估指标看，WNARN预测精度也较高，3个水流序列的RMSE、MAE和MARE分别为0.047～0.053、0.034～0.040和0.042～0.050，而改进NARN2的RMSE、MAE和MARE却分别为0.200～3.067、0.156～2.375和0.176～2.619(见表2)。评估结果进一步显示，华县和临潼序列改进的NARN2各预测误差项优于未改进的NARN1，但咸阳序列NARN2预测精度不及NARN1。

表3 WNARN和NARN模型预测性能极端错误指数评估结果

WNARN的AREmx和AREmn分别为0.001～0.126和0.001～0.211，均优于NARN1和NARN2的结果，进一步表明WNARN对每个时间点上的预测精度均优于NARN(见表3)。AREmxd和AREmnd的评估结果显示，NARN模型在华县序列极值预测中略微优于WNARN，但在其他2个序列中NARN结果差于WNARN，表明WNARN在水文序列重大事件预测方面整体上优于NAR。

WNARN向前48个月预测值和观测值对比结果进一步直观显示其不仅可以从整体上对3个水文序列进行了精确的预测，并且在最大值(洪峰)和最小值(干旱)等细节预测上表现也极为突出(见图6)。

图6 WNAR模型的预测值与观测值之间的比较结果

4 结束语

提出一种基于小波非线性自回归神经网络模型(WNARN)的水文序列预测方法，并与单一的非线性自回归神经网络模型(NARN)进行了对比实验。训练结果显示，NARN通过增加隐含层神经元个数改善的模型有可能较好地拟合历史数据，但拟合精度在多评估指标上均不及WNARN。模型的测试评估结果显示，WNARN不仅整体预测能力和精度上优于NARN，而在每个时间点上的预测精度也均优于NARN。另外，结果还发现WNARN对序列极大和极小值的预测表现也较NARN突出，说明WNARN同时具有良好的预测水文序列重大事件的能力。其主要原因在于小波分解把水文序列数据分解为低频层和高频层，从不同的时间尺度上揭示水文长短期变化规律。

该文运用3个水文序列来分析和验证所提出模拟方法的精确性和有效性。未来有必要运用更多情景和序列来对WNARN的模拟预测能力和精度进行试验，以验证此方法的通用性。