交互作用Fock空间l2(Γ,{λn})上的梯度算子和散度算子

赵丹丹,周玉兰

(1.西北师范大学知行学院,甘肃 兰州 730070;2.西北师范大学数学与统计学院,甘肃 兰州 730070)

1 引言

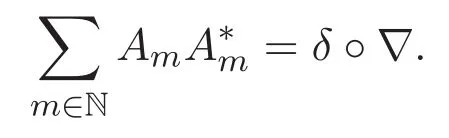
2 预备知识

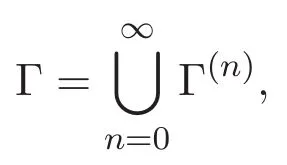
在文章中,用σm 表示σ{m},用σ∪m表示σ∪{m}.

引理 2.1[7]设L2(M,µ)和L2(N,ν)是可分的测度空间,则存在唯一的同构关系

使得f⊗g与f(x)g(y)对应.特别地,当L2(N,ν)为可分的Hilbert空间H 时,有

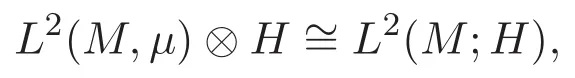
使得f⊗h与f(x)h对应.

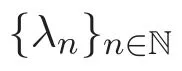
其中 n≥1.由交互因子的定义可知,若λn(x1,···,xn)=0,则

λn+1(x1,···,xn,xn+1)=0,n ≥1.

定义 2.2[6]设 l2(Γ(n)),n=0,1,2,···是 Hilbert空间,则

关于内积

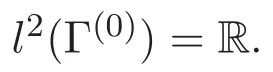
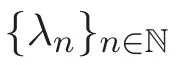
紧接着给出交互作用Fock空间l2(Γ,{λn})上增生算子和湮灭算子的定义.

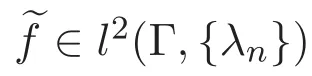
注[6]:(1)1{x1,··,xn}(m)表示示性函数,即

其中n≥1.

(2)在n粒子空间中,湮灭算子把元素变到(n+1)-粒子空间中,而增生算子把元素变到(n−1)-粒子空间中.

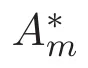
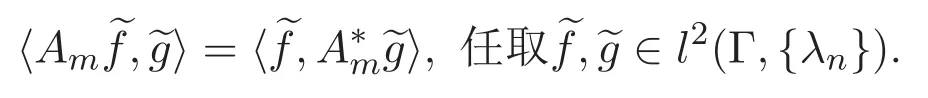
(4)l2(Γ,{λn})上的点态增生、湮灭算子在相同位置具有反交换关系,在不同位置具有交换关系,即

其中 I是 l2(Γ,{λn})中的恒等算子.

由于该空间中交互因子的限制,在

和 Γ(n)之间存在双射.若 σ ={x1,···,xn} ∈ Γ(n),任取 f⊗n(x1,···,xn)∈ l2(Γ(n)),记

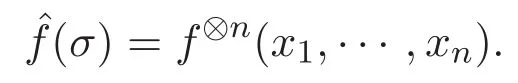
根据文献[8],定义该交互作用Fock空间上的计数算子.

根据文献[5]中积分算子J在Bernoulli泛函空间中的作用,有

命题2.1 设

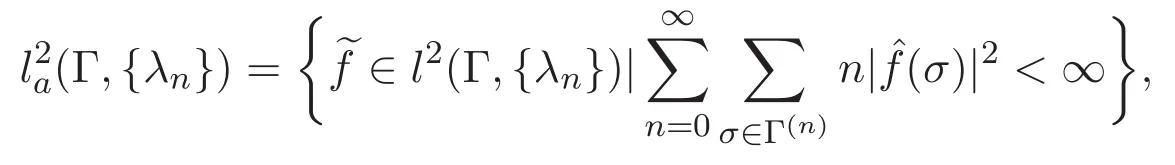
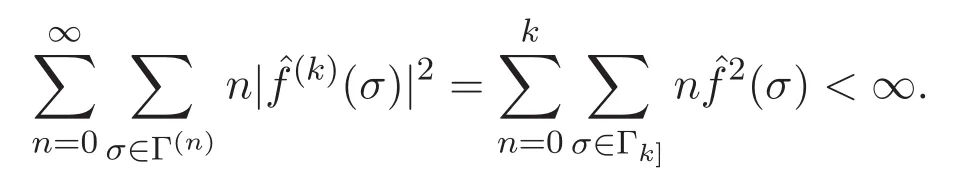
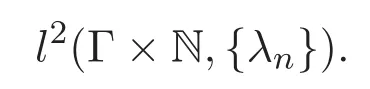
注:当σ={x1,···,xn} ∈ Γ(n),记 Fm(x1,···,xn)=Fm(σ)=F(σ,m). 则上述空间中的内积可表示为

命题2.2 设

3 主要结果

首先,给出交互作用Fock空间l2(Γ,{λn})中梯度算子和散度算子的定义.

下面定理得到l2(Γ,{λn})上梯度算子的性质.

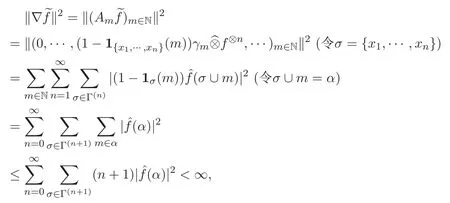
注:(1)根据上述定理证明,有

(2)梯度算子∇不是全空间的线性算子,而是稠定的线性闭算子.

接下来,给出散度算子的定义.

由梯度算子和散度算子的定义,恰好得到散度算子是梯度算子的共轭算子.

定理 3.2 梯度算子∇和散度算子δ互为共轭算子,即

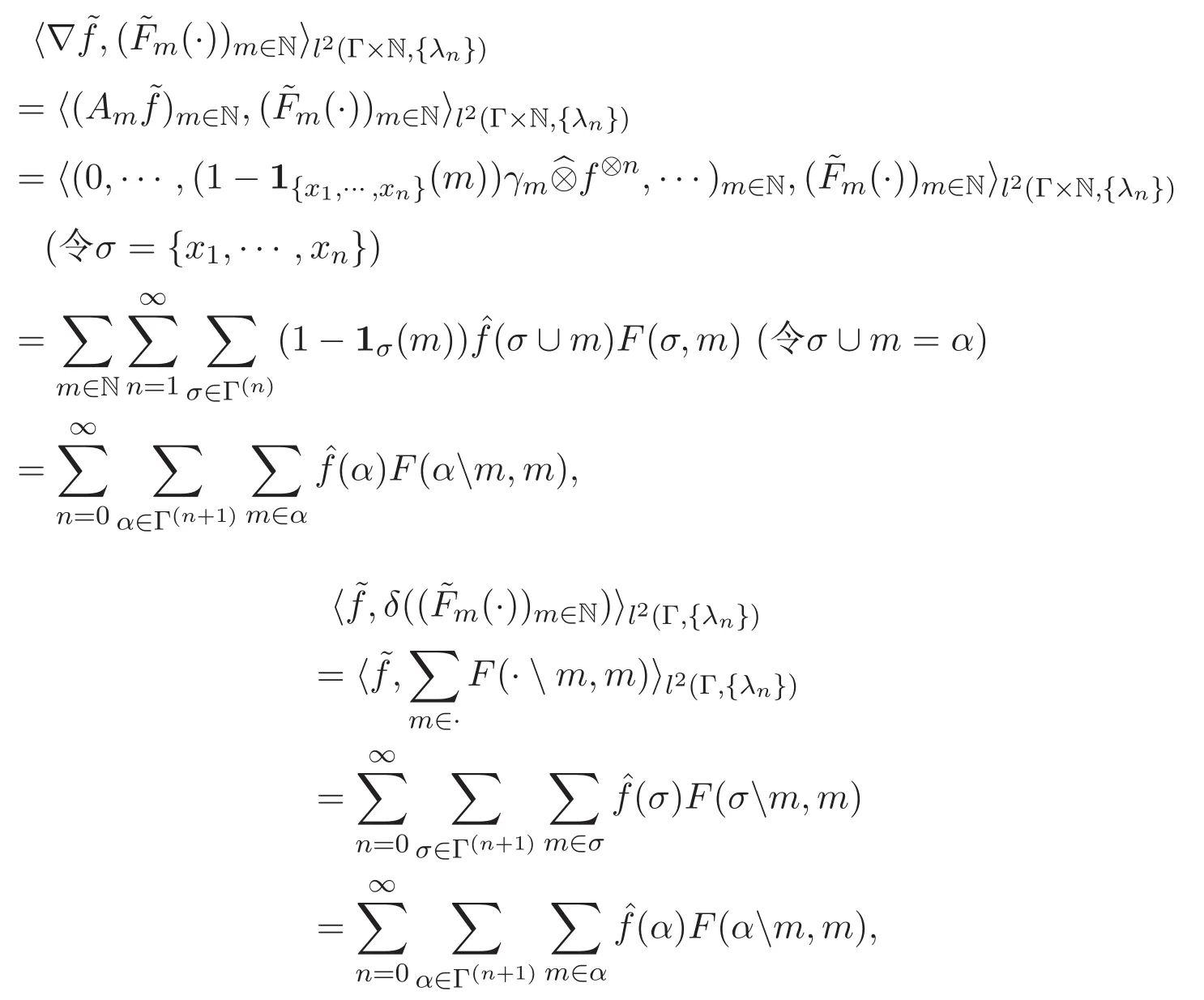
结合文献[9]和定理3.1和定理3.2,有

下面讨论梯度算子和散度算子与计数算子之间的关系.记δ◦∇为梯度算子∇和散度算子δ的复合.

定理 3.3 任取 f⊗n∈ l2(Γ(n),{λn}),则 δ◦∇(f⊗n)=N(f⊗n).

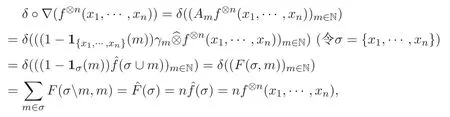
得到 δ◦∇(f⊗n)=n(f⊗n),结合定义 2.4,N(f⊗n)=nf⊗n,故 δ◦∇(f⊗n)=N(f⊗n).

从上述定理中可以看到,在交互作用Fock空间的n-粒子空间l2(Γ(n),{λn})中,梯度算子、散度算子所构成的复合算子δ◦∇与计数算子相等.将δ◦∇作用在l2(Γ,{λn}),有

注:δ◦∇是l2(Γ,{λn})上的稠定的线性闭算子.

最后,根据交互作用Fock空间中增生、湮灭、计数算子间的关系,讨论增生、湮灭算子族与δ◦∇的关系.

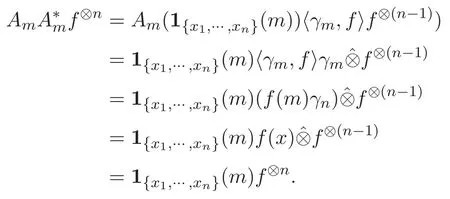
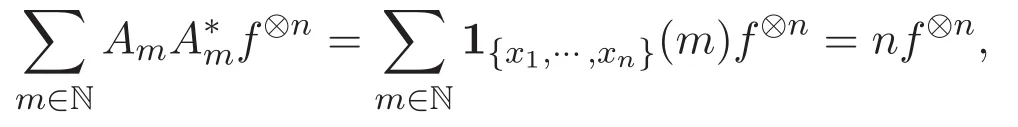
结合计数算子的定义,有

4 总结

l2()是实值平方可和函数构成的 Hilbert空间,文章基于 l2()的交互作用Fock空间l2(Γ,{λn}),定义离散条件下梯度、散度算子并研究其性质,得到