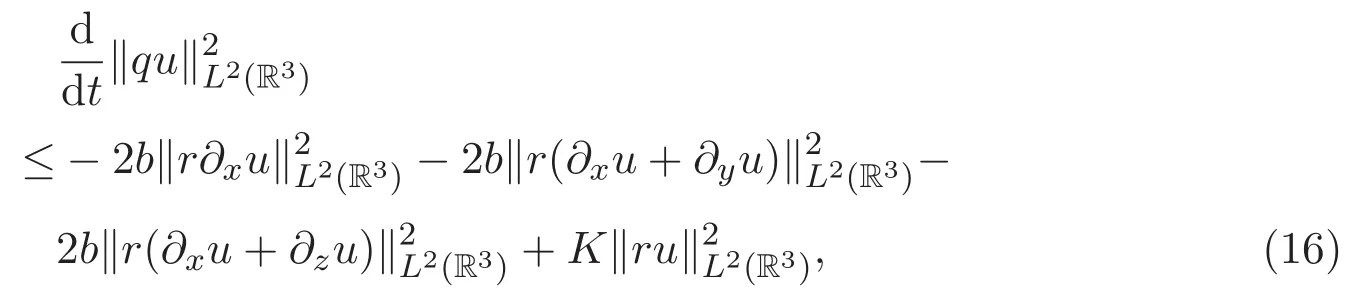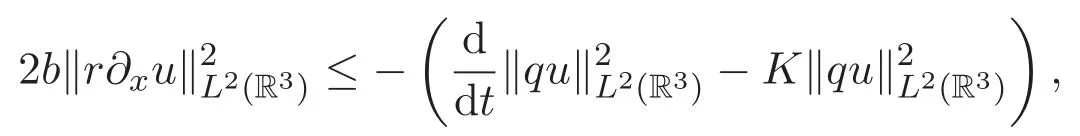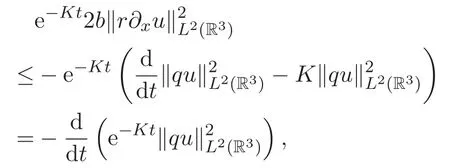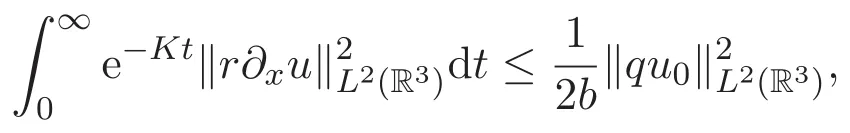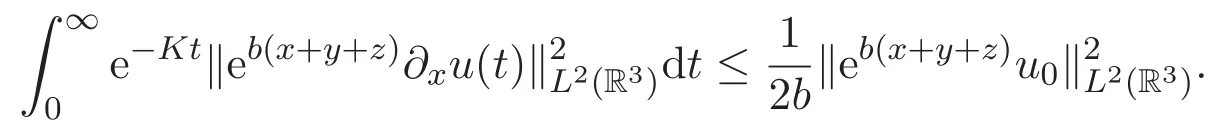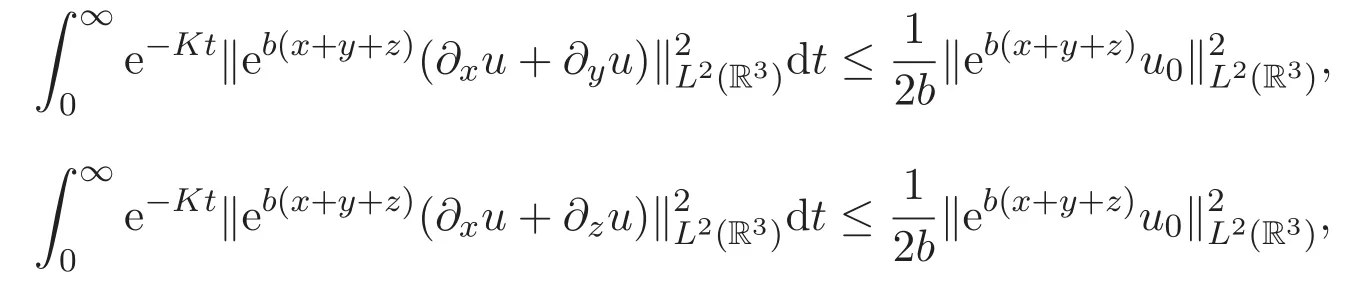三维Zakharov-Kuznetsov方程解的衰减性
2021-04-05种鸽子于浩洋王海权付英
纯粹数学与应用数学 2021年1期
种鸽子,于浩洋,王海权,付英
(西北大学数学学院,陕西 西安 710127)
1 引言
本文考虑三维Zakharov-Kuznetsov(ZK)方程的初值问题:
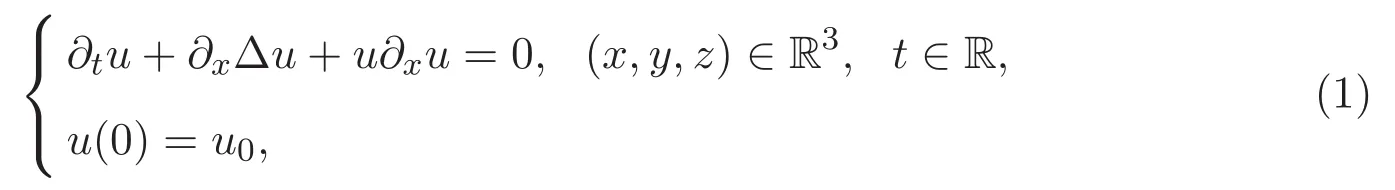

三维ZK方程是Korteweg-de Vries(KdV)方程的三维推广,该方程是由文献[1]从含有冷离子和热等温电子的磁化等离子体中推导出来的.文献[2]得出,该方程描述的是在磁化等离子体中离子声波的传播.
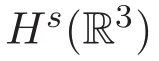
关于指数衰减解,文献[8]证明了:对于β>0,若初值
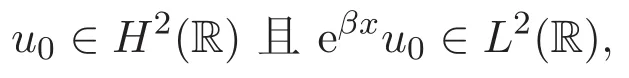
则对应的KdV方程初值问题的一个全局解u满足如下估计
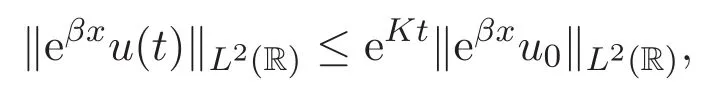
和
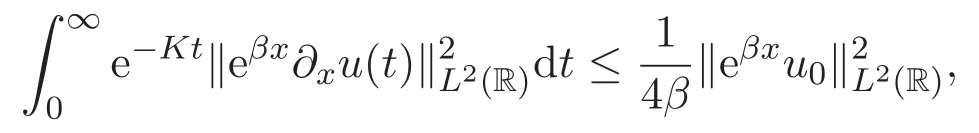
本文的主要目的是研究初值问题(1)解的指数型衰减性,类似于已在文献[8]中讨论的KdV方程解的指数衰减性,现将空间维数升高到三维,即对于三维ZK方程的解是否也有同样的衰减性呢?
2 衰减性
考虑一个一般的三维ZK方程:
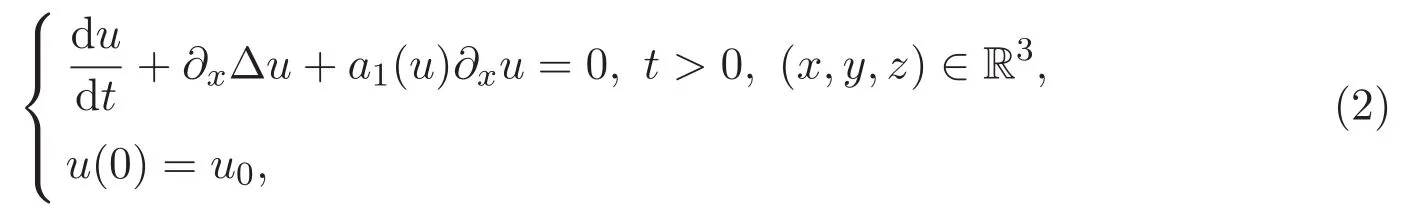

显然,初值问题(2)满足如下守恒律
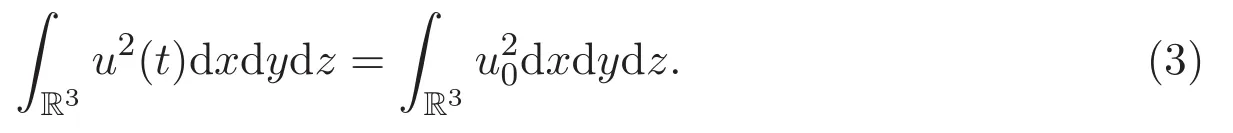
利用文献[8]中类似的方法,可得下面结果.
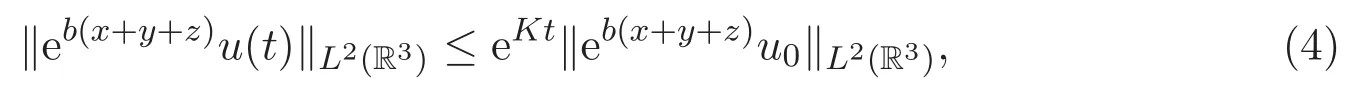
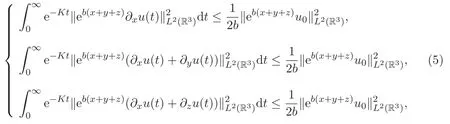
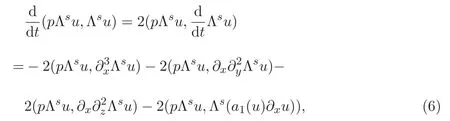
其中
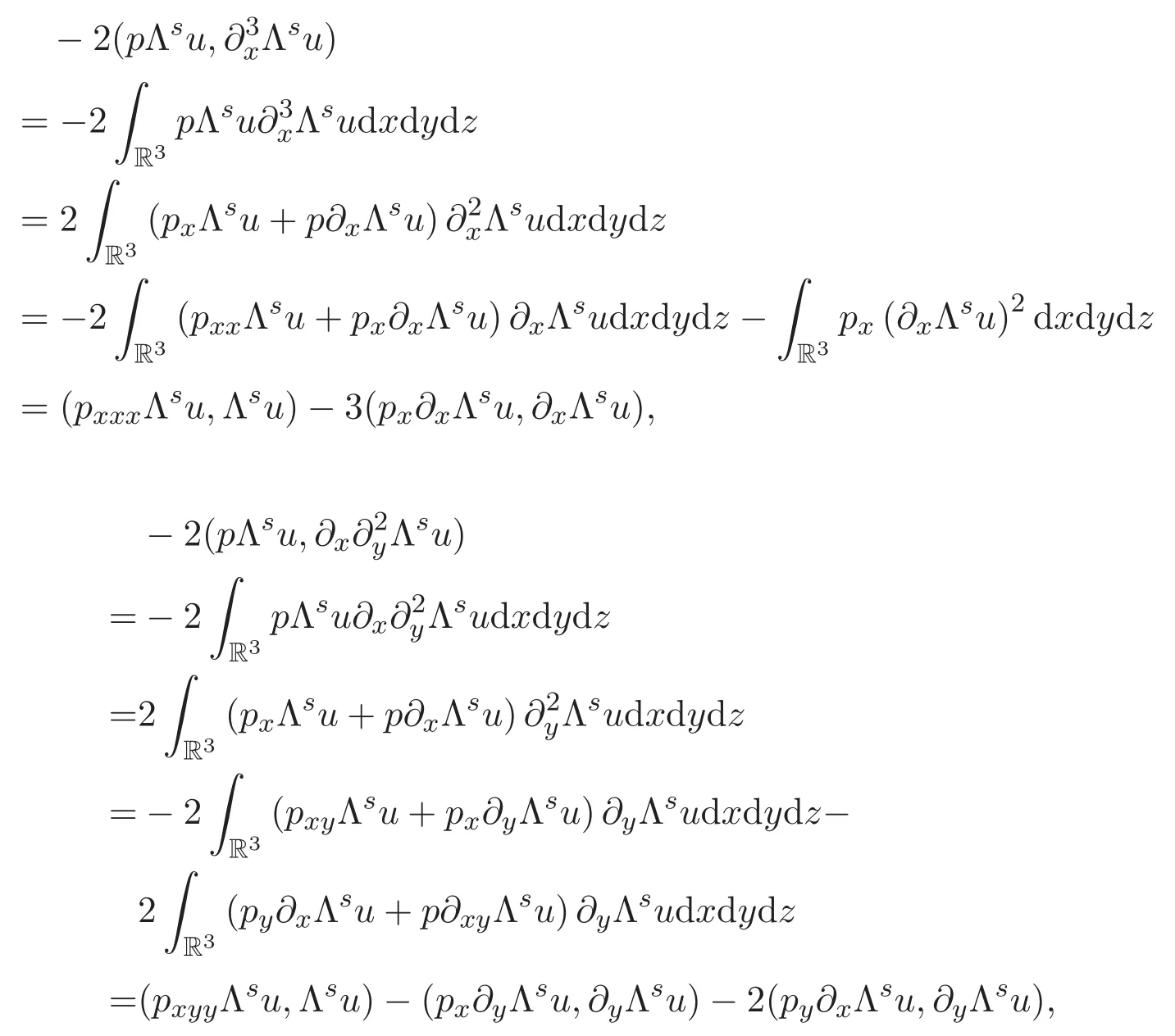
同理可得
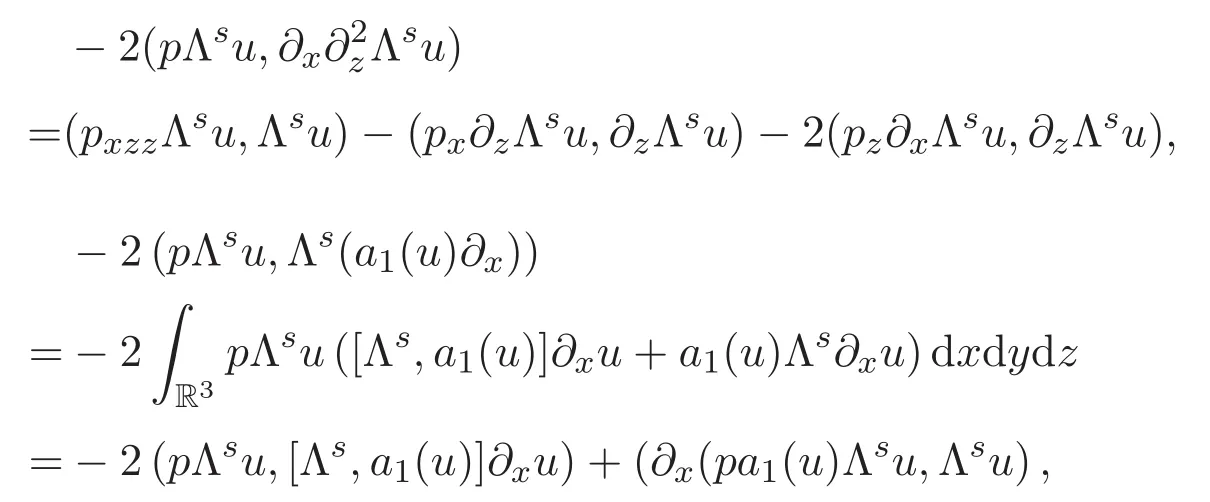
将上面所有结果代入(6)式可得
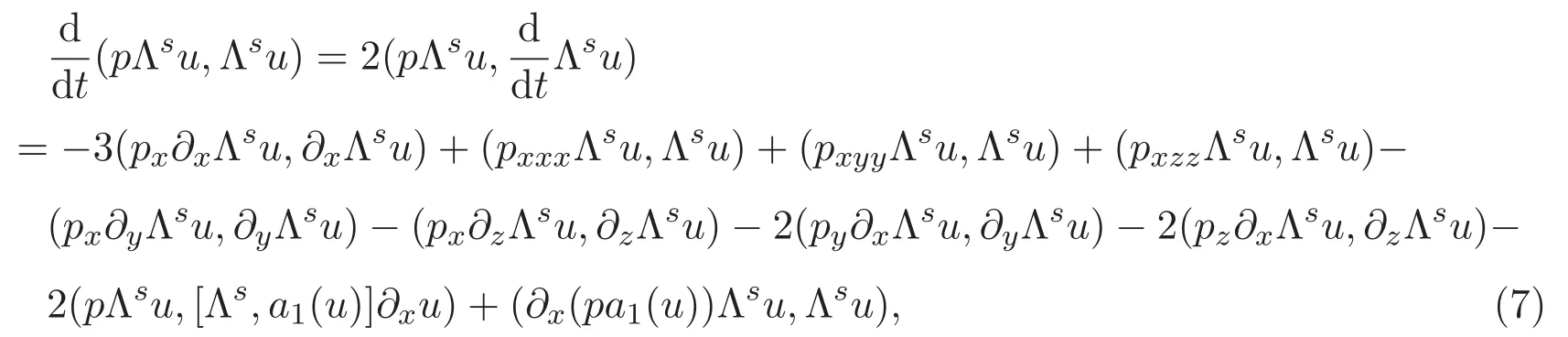
其中[,]为交换子.在(6)式中,令s=0可得
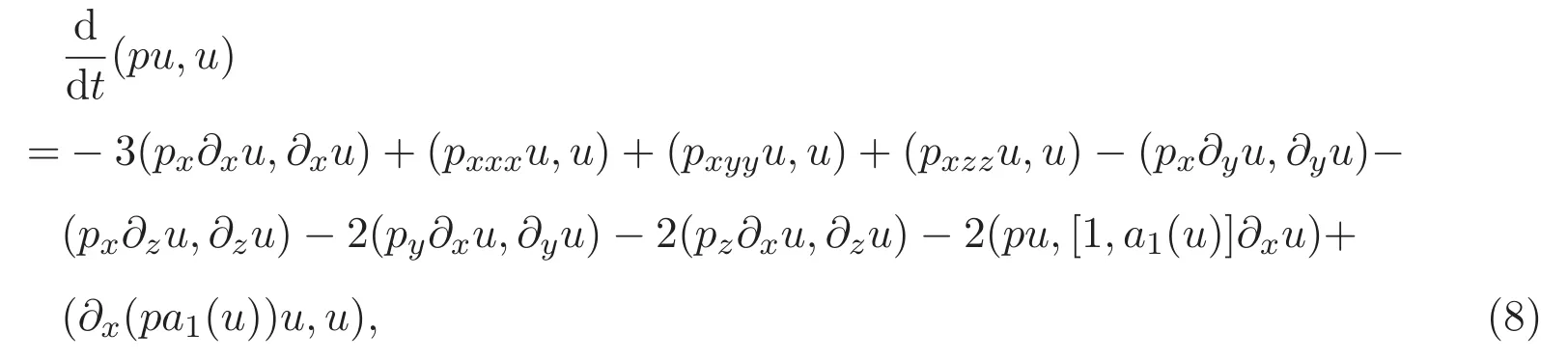
其中
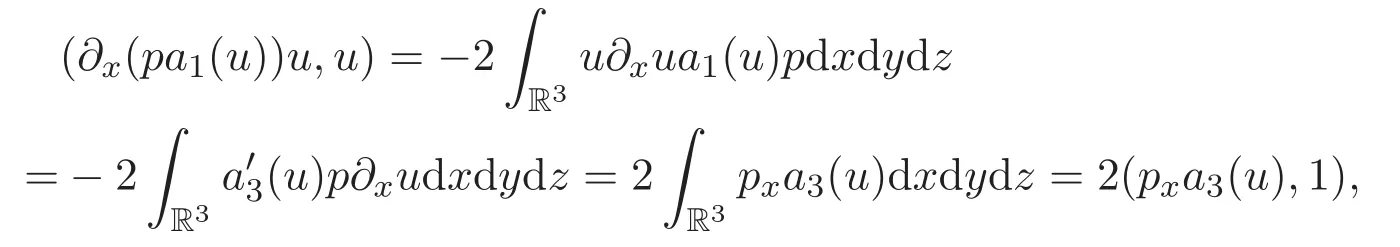
其中a3被定义为
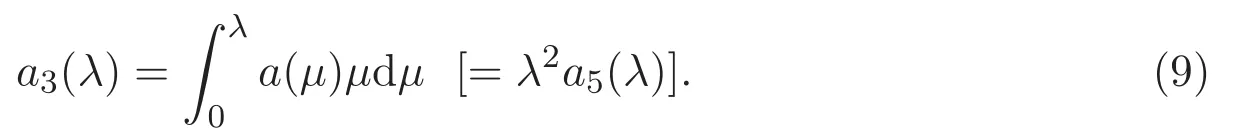
将上面的估计代入(8)式可得
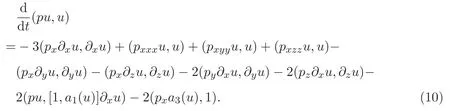
因为eb(x+y+z)是无界的权函数,直接证明相当困难,所以首先用有界的权函数来逼近eb(x+y+z).令
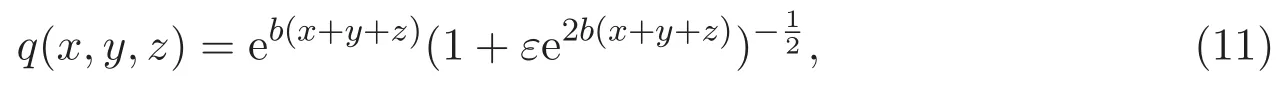
其依赖于参数ε>0.利用辅助函数
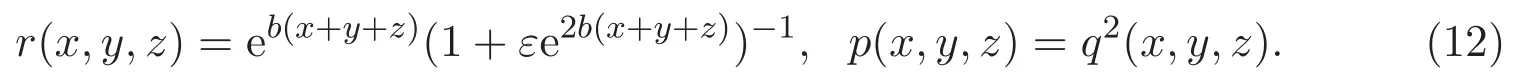
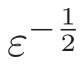
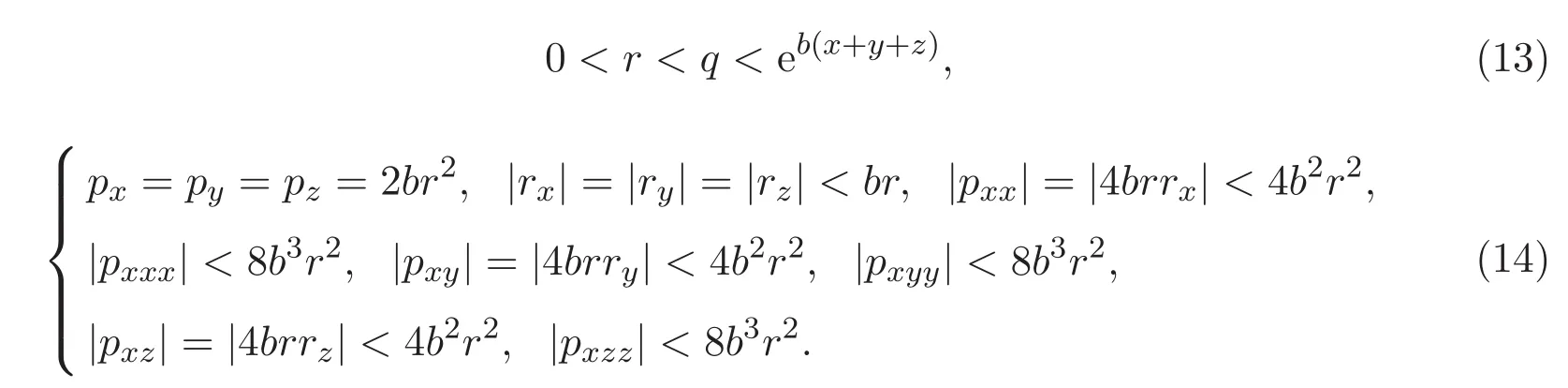
在 (8)式中,令p=q2,利用(14)式及px=py=pz,可得
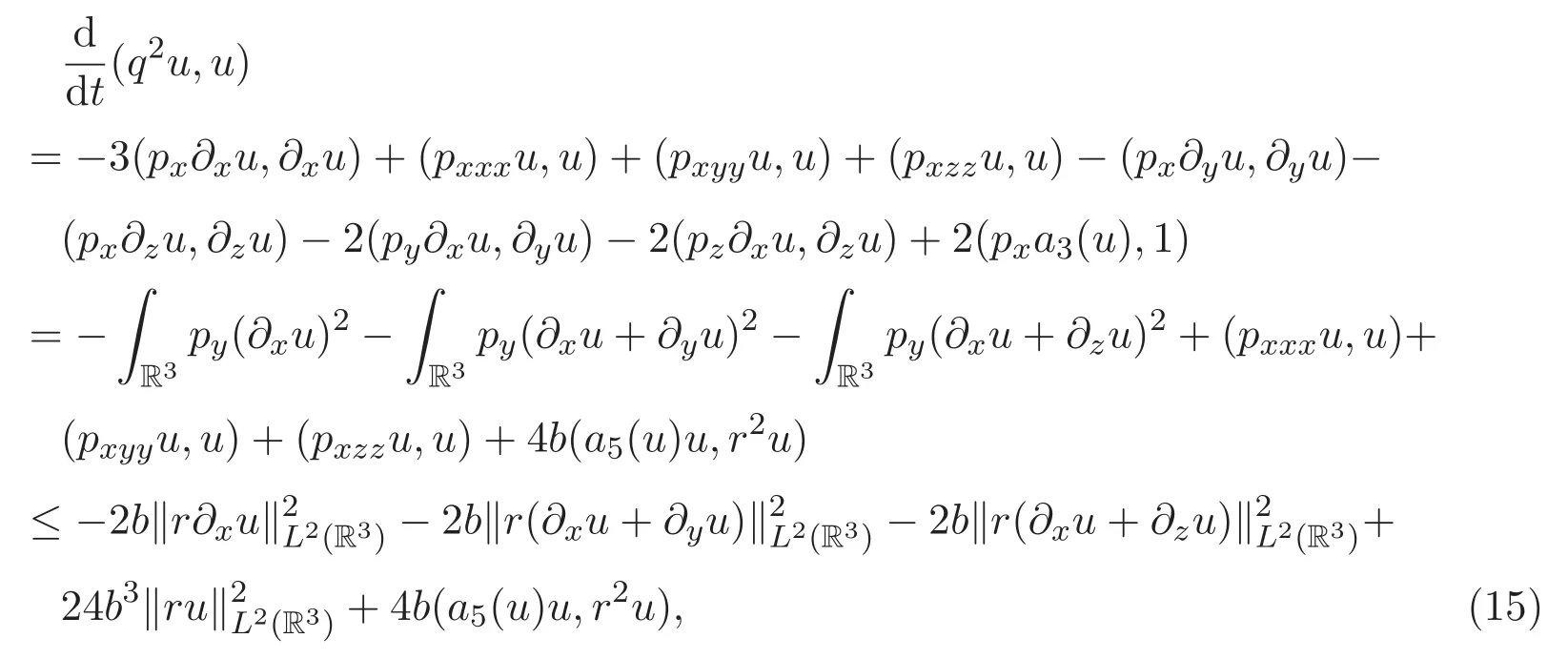
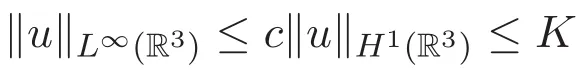
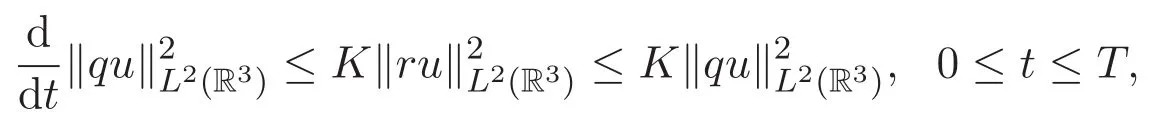
由Gronwall不等式可得
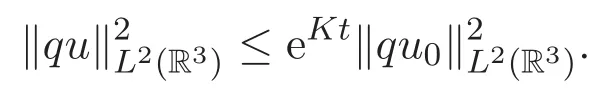
因为K 不依赖于ε,当ε↓0时对上式取极限,由单调收敛原理可得
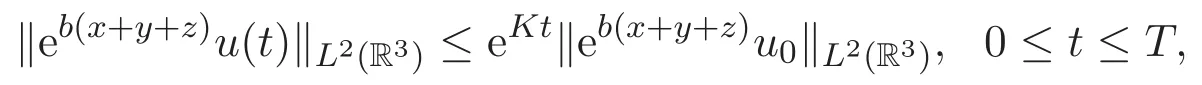
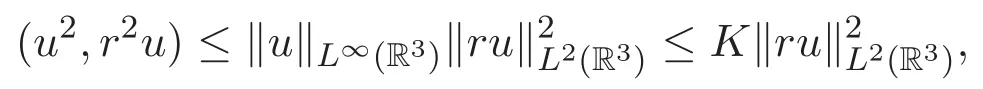
|rx|=|ry|=|rz| 又由(13)式知0 由(16)式可得 进而可得 对上式关于时间t积分可得 因为K 不依赖于ε,当ε↓0时,对上式取极限,由单调收敛原理可得 同理可证 于是,定理2.1得证.