土壤水-汽-热耦合运移的数值模拟研究与验证

乔星华，董晓华，孙 媛，刘旋旋

（1.三峡大学水利与环境学院，湖北宜昌443002；2.水资源安全保障湖北省协同创新中心，武汉430072；3.广东省水文局肇庆水文分局，广东肇庆526060；4.广东省水文局清远水文分局，广东清远511500）

0 引 言

非饱和土壤水分运动一直是水文学、土壤科学和农业领域关注的热点问题，土壤中的水-汽-热耦合运移理论已广泛应用于全球气候变化和生产实践当中[1]。土壤是一个非均质、多相、分散和多孔的系统，水、汽、热在土壤中存在并且以土壤为传导介质进行变化，其中非饱和土壤由固相、液相和气相组成[2，3]。作为土壤水资源补给的重要途径，土壤入渗过程近年来被广泛应用于土壤水资源评价、水文模型构建等相关领域中[4]。

国内外对于土壤水分运动的研究主要考虑的是温度的影响，一些学者对土壤水-汽-热耦合运移规律做出了研究，杨金忠[6]等利用参数的经验值对水、汽、热耦合作用的理论和数值计算进行了研究。水建高[7]等利用非等温的水-汽-热耦合模型模拟了松土条件下土壤水分及温度分布，得到地表处必须考虑温度对水汽流动的影响的结论。曾亦键[8]基于PdV 理论，考虑了土壤内部空气，建立了蒸发条件下土壤水-汽-热-空气耦合模型，分析了土壤水汽运移规律，从理论上完善了非饱和带土壤水-汽-热耦合模型研究。高万德[9]利用Hydrus 建立水-汽-热耦合运移模型，对农田灌溉条件下大埋深包气带的土壤水-汽-热运移规律进行研究。李吉祥等[10]认为包气带水运移涉及液态水和水汽，而土壤水分运动涉及的条件复杂，求解困难，数值方法则是求解包气带水分运移的主要方法。MALIK[11]提出非饱和冻土中水-汽-热耦合模型，得出水汽的迁移依赖于土体内温度梯度和初始含水量的结论。

基于以上研究可以发现，目前很少有针对砂壤土土壤水-汽-热耦合运移的研究。本文开展了室内一维土柱试验，分降雨和蒸发两个阶段，观测了土柱内不同深度处的含水率、温度、气压的变化过程，蒸发阶段的蒸发速率，以及包括空气温湿度、风速、大气压强等环境气象因子；应用土壤水-汽-热耦合模型，使用上述观测数据对模型参数进行率定，对降雨和蒸发两种情景下的土壤水-汽-热耦合运移进行模拟，利用试验得到的土壤温度和含水率对模拟值进行验证。本研究所得结论可为砂壤土土壤水-汽-热耦合运移提供理论基础，同时为农业灌溉领域提供理论参考依据。

1 材料与方法

1.1 试验材料

土样取自三峡大学校园，选取多个地形点进行采样，清除采样点处表面覆盖物并用环刀[12-17]取深度为5～15 cm 间的土样，将所有土样放在洁净的塑料板上均匀混合，经过风干、磨碎并过2 mm 标准筛网后密封保存[18]。本试验采用筛分法与密度计法相结合分析土壤颗粒，确认试验土样为砂壤土，采用环刀法测得土样的容重为1.409 g/cm3，由达西公式得到该土壤的饱和渗透系数为Ks=0.355 mm/min。供试土样的基本物理性质见表1。

表1 供试土样的基本物理性质Tab.1 Basic physical properties of the test soil sample

1.2 土柱试验方法

土柱实验于2019年6月在室内进行，将处理后的土样放到土柱筒中，土柱筒的高度为80 cm，直径为14 cm。采用了模拟人工降雨蒸发的方法。

试验分为降雨和蒸发两个阶段。第一阶段为降雨阶段，降雨强度为12 mm/h，采用马氏瓶恒定供水，首先进行2 h 降雨，在降雨之前对降雨装置进行率定，降雨强度是通过调整马氏瓶的高度来控制的[19]；第二阶段为蒸发阶段，蒸发阶段的光照辐射由距离土柱顶端5～10 cm 的远红外灯提供，为了测量土壤的蒸发速率，将土柱置于高精度电子天平之上，蒸发时间为4 h。分别在土柱距离顶端3、8、18、28、48 cm 处放置TDR 探头、温度探头和气压探头。降雨和蒸发阶段周期均为48 h，且降雨和蒸发均在距离开始监测各项指标的第10 h 进行。试验数据的测量由TDR 传感器（含水率、温度）、气压传感器（空气压强、土壤气压）、手持式气象站（空气温度、空气湿度、风速等）、高精度电子天平测得（蒸发速率）。

1.3 数值模拟方法

由室内土柱模型监测并记录得到降雨和蒸发阶段的环境气象因子、土壤含水率、土壤气压和土壤温度等。STEMMUS模型[8]是曾亦键提出的模拟不饱和土壤中液态水、水蒸气、干燥空气和传热耦合的程序，由数值模型控制方程（包括土壤水分运动方程、干空气平衡方程、能量平衡方程）构成，考虑温度影响的土壤水分特征曲线模型影响着模型的控制方程。土壤水分特征曲线考虑常温（20 ℃）影响，修改模型中的土壤的残余含水率θr、饱和含水率θs和经验拟合参数α和n的经验参数，利用试验结果对STEMMUS 的参数进行率定，得到精度较高的模拟结果。

1.3.1 数值模型控制方程

（1）土壤水分运动方程。STEMMUS 模型中对土壤水分运动公式的改进形式为：

式中：ρL、ρV分别为液态水、水汽密度，kg/m3；θL为体积含水率，m3/m3；θV为土壤空气体积，m3/m3；qL、qV分别为液态水、水汽的通量，kg/(m2·s)；t为时间，s；z为垂向坐标轴，m。

（2）干空气平衡方程。STEMMUS 模型中考虑了土壤中空气的传输及影响过程，在非饱和土壤中空气运移的驱动力为空气密度梯度和气压梯度[8]。其表达式为：

式中：ρda为干空气密度，kg/m3；Hc为Henry常数，对于空气，在标准大气压、25 ℃条件下，其值为0.02；qa为干空气通量，kg/(m2·s)；

（3）能量平衡方程。温度在土壤中的传输的形式主要包括传导、辐射和对流，非饱和土壤能量传输包括土壤固相、液相、干空气和水汽的热运移及湿润热[20]。非饱和土壤中的能量传输方程可表达为：

式中：λL、λs、λg为固、液和气的热传导系数，W/(m·℃)；θs为土壤固体体积分数；θa为土壤空气体积分数，θa=θV=ε-θL；cs、cL、ca、cV为固、液、水汽、气的比热，J/(kg·℃)；T为参考温度，℃；ρs为土壤固体密度，kg/m3；L0为参考温度T时的蒸发潜热，J/kg；W为局部湿润热，J/kg，λeff为包含固、液、气的有效热传导系数，W/(m·℃)。

1.3.2 温度影响下的土水特征曲线模型

本研究通过对VG 模型的经验拟合参数n和α、土壤的残余含水率θr、饱和含水率θs进行修改使模拟结果达到最优化。由于试验在室内进行，室内温度在20 ℃左右，因此当考虑温度为20 ℃（工程上的常温状态）时，对影响土壤水分特征曲线的土壤残余含水率θr、饱和含水率θs和经验拟合参数α和n进行修改。

美国学者Van Genuchten 在1980年提出了描述土壤水分特征曲线的VG模型[22]，其表达式为：

式中：θr为残余含水率；θs为饱和含水率；α、m和n为经验拟合参数。

考虑温度影响时，土壤残余含水率θr、饱和含水率θs和经验拟合参数α经验公式如公式(5)～(7)所示，其中温度T为20 ℃（模型中用开氏温度293.15 K计算）。

由公式(5)～(7)可以将VG模型改写成式(8)：

式中：αT为20 ℃下的经验拟合参数；θrT为20 ℃下的残余含水率；θsT为20 ℃下的饱和含水率。

1.3.3 初始条件和边界条件

(1)初始条件。土壤初始条件是在时间t=0 时，土壤在0 -L土柱总长度为L）时的土壤测得的各项参数，包括土壤含水率、土壤温度、土壤气压，大气温度、湿度、空气压强等。

(2)上边界条件。本文中土柱上表面为开放型表面，选择第二类边界条件，其表达形式为：

式中：E为时间为t时的蒸发速率，kg/(m2·sm2·s)；P为时间为t时的降水速率，m/s；t为时间，s。

土壤蒸发量由式(10)推求，主要是根据大气阻力和土壤对水汽的阻力计算：

式中：ρVS为土层表面的水汽密度，kg/m3；ρVa为大气中的水汽密度，kg/m3；ra为大气阻力，s/m；rs为土层表面对水汽的阻力，s/m；f是常数，值为0.41；U为风速，m/s，Zm为测量的风速所在高度，m；d为零平面位移，m，如果为裸地，其值为0；Zom为表面粗糙长度（动量通量），取值0.001 m；ψsm为大气稳定性修正系数（动量通量）；Zoh表示表面粗糙长度（热通量），取值0.001 m；ψsh为大气稳定性修正系数（热通量）；rsl为水分子由水层表面扩散到空气中所遇到的阻力，取值10 s/m；为拟合系数，取值35.63；θmin为土壤最小含水率，取值0.15 m3/m3；θsur为土壤表层含水率，m3/m3。

空气方程边界条件为第一类边界条件，表示为：

式中：Pg为时间为t时的空气压强，Pa；Γ为大气-土壤边界。

温度传导方程的边界条件为第一类边界条件，表示为：

式中：Ts为时间为t时的地表温度，℃。

(3)下边界条件。本次试验采用的土柱筒下设有排气阀，当土壤底部含水率达到饱和时，可以自由排出。对于土壤水分运动、土壤温度传导、空气传导的下边界条件可以写成公式(15)～(17)的形式：

1.3.4 时空离散

实验选用均质砂壤土，土壤深度为70 cm，将土柱离散为25 个节点，由上至下节点间距依次增大。土壤表层的分层厚度为0.25～0.5 cm，土壤中上层的分层厚度为1 cm，土壤中下层分层厚度为2 cm，土壤下层的分层厚度为5～10 cm，将时间步长设为1 s。

1.3.5 模型基本参数

模型的基本参数参考Rosetta 数据库的砂壤土水力特征参数[23]，修改后的经验参数，模型基本参数如表2所示。

表2 模型基本参数Tab.2 Basic parameters of the model

1.3.6 模型求解

1.3.7 模型精度验证

选用平均相对误差(AVRE)、相对均方根误差(RRMSE)作为误差指标对降雨和蒸发阶段含水率和温度的实测值和模拟值进行误差分析[24]。当RRMSE=0时，模拟值与实测值完全吻合，RRMSE＜10%时，模拟值与实测值的一致性很好，10%～20%为比较好，20%～30%表明模拟效果一般。AVRE值越接近于1，说明模拟效果越好[25]。

式中：Ci为模拟值；Mi为实测值；Nw为总的样本观测数。

2 结 果

图1为降雨和蒸发阶段空气温度的变化情况。

分别对降雨和蒸发阶段的土壤水分和土壤温度同时进行模拟，得到如下结果：

图2为降雨阶段土壤含水率和温度的模拟图，可以看出，降雨开始3～28 cm深度的土壤含水率明显增加，降雨结束后随着土壤水分向下层传播，各层的土壤含水率开始变小，减小到一定程度，各层土壤含水率接近于一个恒定值，而48 cm 处的含水率上升到一定值后保持恒定不变；降雨阶段大气温度高于土壤的温度，在这个时间段内各层土壤的温度呈上升趋势，这种土壤温度升高随着降雨入渗而向土柱深处传播。

降雨阶段各层土壤含水率和温度的总体模拟效果较好。其中土壤含水率随着深度的增加，模拟精度变高，土壤含水率的实测值在降雨的再分布阶段略高于实测值。土壤温度在3 cm 处、8 cm 处的模拟效果相对较好，其余各层的温度模拟值与实测值均有偏差，并且模拟精度随着深度的增加而减小。

自改革开放以来，中共中央1982年至1986年连续5年发布以“三农”(农业、农村、农民)为主题的中央“一号文件”，2004年至2018年又连续15年发布以“三农”为主题的中央“一号文件”，不断指导“三农”改革创新。“一号文件”某种意义上已成为中共中央重视“三农”工作的专有名词。

表3为降雨阶段土壤含水率和温度的模拟结果，可以看出，各层土壤含水率和温度的平均相对误差都接近于1。对于含水率的模拟，18 cm 以下深度的相对均方根误差都小于10%，模拟效果很好；8 cm 处的相对均方根误差在10%～20%之间，模拟效果比较好；而3 cm 处的相对均方根误差在20%～30%之间，模拟效果一般。对于温度的模拟，各层的相对均方根误差均小于10%，模拟效果很好。

图3为蒸发阶段土壤含水率和温度的模拟图，通过监测空气温度的变化，空气温度从第5 h 开始升高，导致土壤上层含水率开始减小。土壤其他层含水率变化规律类似，深度越大，土壤含水率变化幅度逐渐减小，中下层土壤含水率几乎无变化。加热开始时，土壤表层3 cm 处温度迅速升高并逐渐达到最大值。加热结束时，土壤表层3 cm 处温度迅速降低，最终温度与室温达到一致。土壤8 cm 处的温度在10.5 h 左右开始上升，在第14.5 h 处升至最大值；土壤18 cm 处的温度在第12 h开始上升，在第16 h处达到最大值，中上层各层温度最终都减小到室温，且温度减小的趋势逐渐变缓；28 cm 处的温度有较小的变化；而土壤48 cm处的温度几乎没有变化。

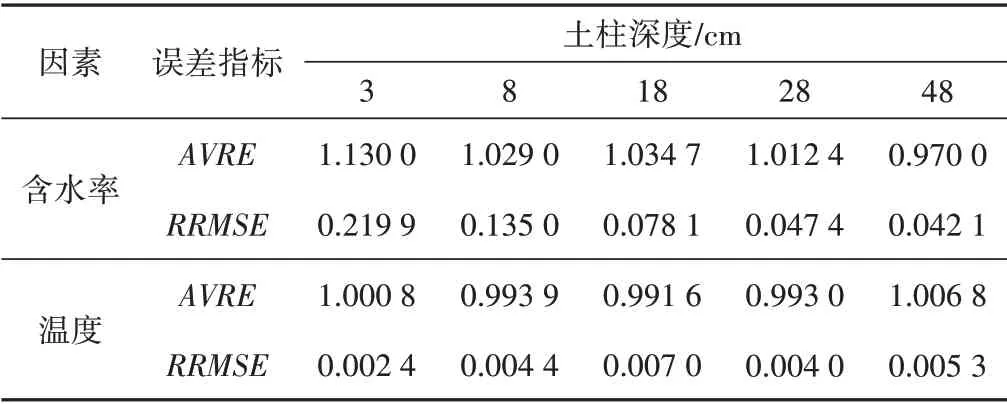
表3 降雨阶段含水率和温度模拟结果Tab.3 Moisture content and temperature simulation results duringrainfall

这一阶段土壤各层的含水率模拟效果较好，且下层土壤含水率的模拟精度高于上层的模拟精度。3 cm 和8 cm 处温度模拟值与实测值非常接近，模拟效果较好，但随深度的增加，温度的模拟值偏差也在增加，由图3（b）、图3（d）、图3（f）、图3（h）和图3（j）可以看出28 cm 和48 cm 处在蒸发开始后的拟合效果很差，在17 h后模拟值均大于实测值。

表4为蒸发阶段土壤含水率和温度的模拟结果，可以看出，土壤含水率的模拟值和上层土壤温度的平均相对误差都接近于1。对于含水率的模拟，各层相对均方根误差均小于10%，模拟值与实测值一致性很好。对于温度的模拟，中上层的相对均方根误差均小于10%，模拟效果很好；但28 cm 处和48 cm 处的相对均方根误差在20%～30%之间，模拟效果一般。

3 结 论

本文开展了室内一维土柱试验，分降雨和蒸发两个阶段，观测了土柱内不同深度处的含水率、温度、气压的变化过程，蒸发阶段的蒸发速率，以及包括空气温湿度、风速、大气压强等环境气象因子；然后应用STEMMUS 模型，使用上述观测数据对模型参数进行率定，获得了较好的模拟精度。主要结论如下：

（1）降雨阶段，土壤温度受大气温度的影响较大。本实验中，大气温度高于土壤温度，雨滴进入土壤后，导致土壤温度升高，这种土壤温度升高随着降雨入渗而向土柱深处传播。

（2）蒸发阶段，在光照辐射的作用下，土柱内各层土壤的含水率缓慢下降；土柱表层土壤温度迅速上升，热量向土柱深层传播，使深层土壤温度逐次上升。

（3）降雨阶段含水率和温度的模拟效果优于蒸发阶段。降雨阶段含水率、温度模拟精度都“比较好”或“很好”，只有3 cm 处的表层土壤含水率模拟精度为“一般”（RRMSE为21.99%），原因是表层土壤的质地不均匀所致；蒸发阶段含水率和温度大部分深度模拟精度“很好”，只有深层（28 及48 cm 处） 的温度模拟精度为“一般”（RRMSE为21.18%及22.92%），原因应该是土柱下部会受环境温度显著影响所致。

表4 蒸发阶段含水率和温度模拟结果Tab.4 Moisture content and temperature simulation results in the evaporation stage