基于二叉空间划分的异常数据检测算法
2021-04-02周万里王子谦谢婉利谭安祖余节约
周万里 ,王子谦 ,谢婉利 ,谭安祖 ,余节约
(1.温州医科大学附属眼视光医院 信息管理处,浙江 温州325000;2.浙江方圆检测集团股份有限公司 检测部,浙江 杭州310000;3.杭州电子科技大学 数字媒体学院,浙江 杭州310000)
0 引言
无线传感网络(Wireless Sensor Networks,WSNs)[1-2]是由多个具有感测能力的微型节点构成的。这些节点部署在不同位置,并且它们感知周围环境数据(如温度、压力、湿度),再以无线通信方式将数据传输至信宿[3]。
传感节点感知的数据通常存在空间相关性和时间相关性[4]。 由于所感测数据的不完整、不准确,甚至异常[5-7],通过时间分析所感测数据显得尤其重要。 产生异常的原因有两种:(1)传感节点的故障;(2)异常事件的发生,如森林发火、洪水。 节点故障产生的异常是独立的,属个体。而异常事件的产生的异常具有空间或时间相关性。因此,通过分析感测数据间的相关性,能够提高对事件检测的准确性。
所谓异常,是指不同于正常数据。 通过对异常数据和正常数据间的等级测量(Ranking Measures,RM),能够检测异常事件。 既可通过局部传感节点分布式识别异常,也可利用观察节点集中式识别异常。
空间分割常用于事件分类。而二叉空间划分(Binary Space Partition,BSP)就是对空间中的物体进行二叉递归划分的算法。 即用平面将空间分割,空间中各部分又被分为前面和后面两类,对分割后的空间继续使用相同的方法进行分割,直到不能分割为止,进而产生BSP 树[8]。
通过BSP 树和质量等级的测量可检测异常。 文献[9]最初利用MassAD 算法进行质量估计,它将数据实例划分为严重异常至完全正常。然而,相比于高质量数据,低质量数据属异常的概率更高。
为此,提出基于二叉空间划分的异常数据检测(Binary Space Partition-based Anomaly Detection,BSP-AD)算法。BSP-AD 算法利用二叉空间划分训练数据,构成正常数据的区间范围,再通过此区间范围检测异常数据。 仿真结果表明,提出的BSP-AD 算法能够准确地检测异常数据,并控制数据存储成本和计算成本。
1 系统模型
令τj表 示 第j 棵BSP 树。 t 棵 树 构 成 树 集γh,即|γh|=t,其中h 表示每棵树的高度。

树中每个节点代表一个子空间。 用md表示在子空间内正常数据实例的个数,而d 表示子空间的深度。 令pd表示深度为d 的子空间的分割点。
令xni表示在训练阶段中第i 个正常数据实例。 用φ项数据实例构成集η,即|η|=φ:

每个实例xk有t 分。 为此,令Sk表示分数集:

例如,S1(xk)表示在树τ1中实例xk的分数,S2(xk)表示在树τ2中实例xk的分数。
依式(4)将所有树上的分数进行融合,再传输至实例xk:

2 BSP-AD 算法
BSP-AD 算法由训练和测试两个阶段构成。 在训练阶段,利用正常数据实例建立参考树,并定义异常检测的主要参数。 而测试阶段,判断给定数据为正常或异常。
2.1 训练阶段
首先,计算每个给定实例xk的分数。 对于任意树τj∈γh,在每个层次,将实例xk与分割点pd-1进行比较。如果xk小于pd-1,就将数据移至左边的子树;否则,就移至右边的子树。 因此,可得外部节点的分数:

如图1 所示,假定实例x=2.50,首先与它的分割点值p=2.54 值进行比较,由于x=2.50<2.54,它遍历左边树,再与第二级的分割点值p=2.43 进行比较,由于x=2.50>2.43,它遍历右边树。
再计算实例xk的质量。 实例遍历了所有树,其在每棵具体树上具有分数。 因此,可利用式(6)计算实例xk遍历在所有树上的平均分。


图1 数据实例的遍历示意图
其中,j∈{0,…,t}。
最后,计算正常实例的范围。 一个实例的质量(Mass)决定了该实例是否为异常。 先给正常数据样本设置质量范围[Minb,Maxb]。 如果某实例质量越出此范围,则判定为异常。 图2 给出了计算正常范围的上限Minb和下限Maxb的过程。

图2 算法过程
令η 为正常数据样本、Ψ 为样本尺寸、t 为树的个数。 先依式(7)计算Mi和MΨ:
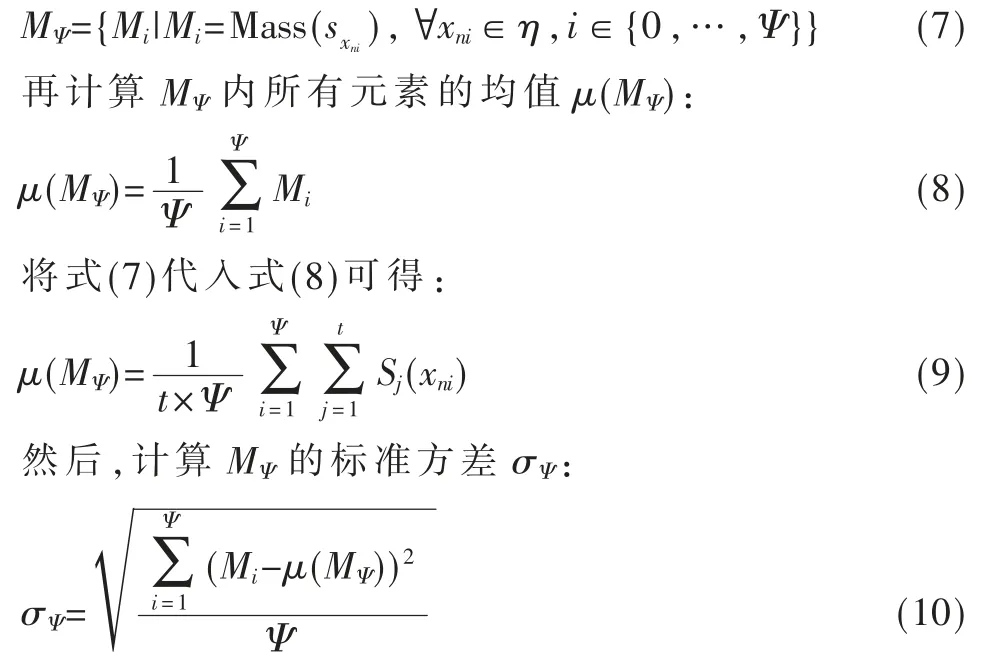
最后,依据μ(MΨ)和σΨ计算Minb、Maxb:

2.2 分割点的选择
令Hmin和Hmax表示空间H 的上下限。 令rand 表示在[Hmin,Hmax]区 间 的 随 机 数。 引 用 文 献[9]的 分 割 算 法。 将分割点p 作为[minp,maxp]区间的中点,其定义如式(12)所示:

其中,r=2×max{(rand-Hmin),(rand+Hmax)}。
2.3 测试阶段
测试阶段判断每个新数据实例xk是否为异常。每个新数据实例xk遍历γh内所有BSP 树。 再计算Sk集的质量,再依据式(13)计算标志位:

如果Anom(xk)=0,则认为实例xk是正常的;否则,如果Anom(xk)=1,则认为实例xk为异常的。 整个过程如图3 所示。
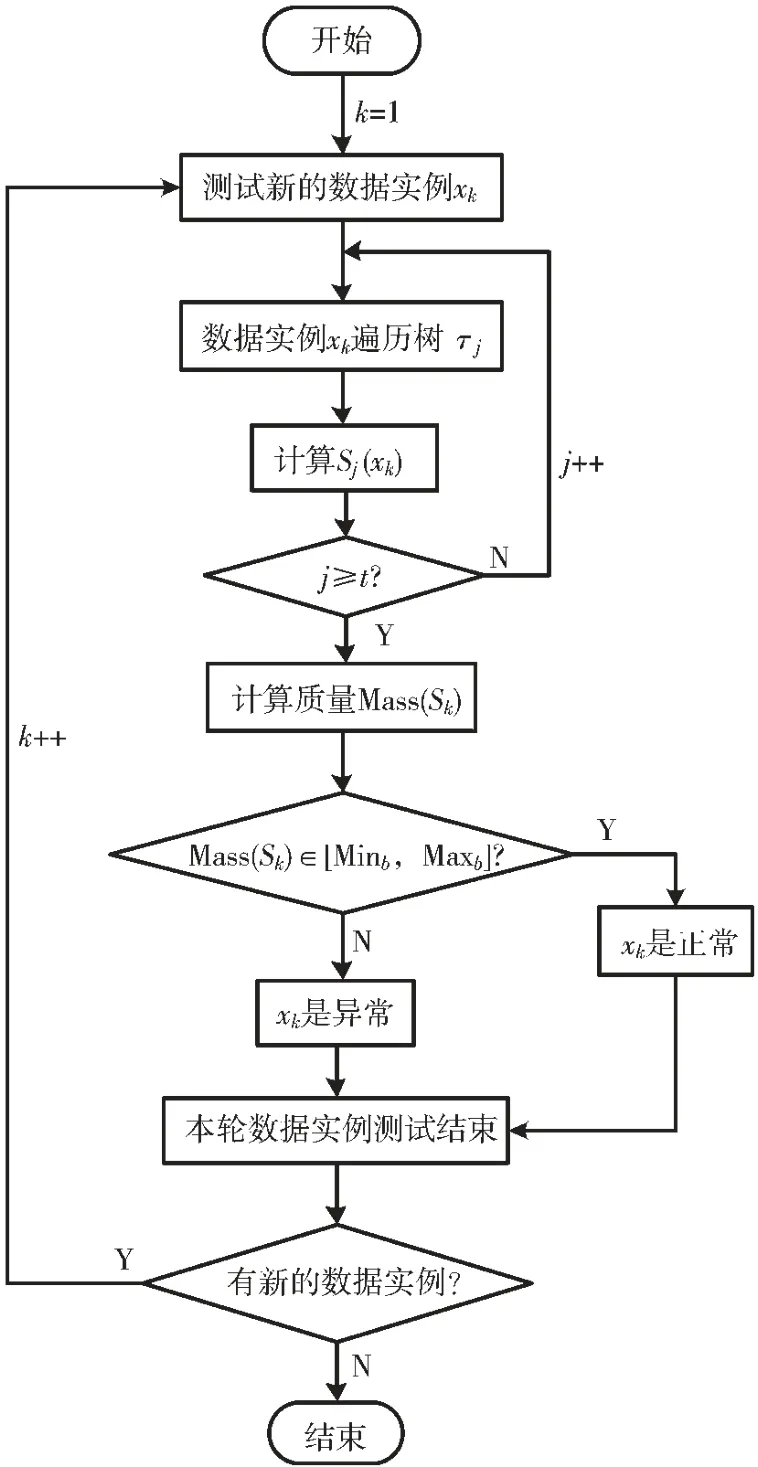
图3 测试阶段流程图
3 性能分析
3.1 仿真环境
利用MATLAB R2018a 软件建立仿真平台,引用文献[9]-[10]所设的BSP 树,其参数为:t=100,φ=256,h=2。同时选择文献[11]提出的基于局部滤波器的检测(Identifying Density-based Local Outliers,IDLO)和文献[9]提出的质量估计(Mass Estimation,MAES)算法作为参照,并对比分析它们的性能。
主要考查真阳性率(True Positive Rate,TPR)、假阳性率(False Positive Rate,FPR)、曲线下面积(Area Under Curve,AUC)和F1 分数(F1 Sorce,F1S)。
TPR 反映了将异常实例准确地检测为异常实例的准确性,其定义如式(14)所示:

其中,TP 表示假阳性率(False Positives,FP),其等于正常的数据实例被错误地判定为异常实例;而伪阴性(False Negatives,FN)等于将异常实例错误地判定为正常实例的概率。
FPR 反映了将正常实例错误地检测为异常实例的概率,其定义如式(15)所示:

其中,TN 为真阴性,其表示异常实例被错误地判定为正常实例。
而AUC 等于在不同点上的FPR 与FPR 之比。 此外,F1S 为准确率与召回率间的调和均值(Harmonic Mean)。F1S 的取值在0~1 之间。 F1S 值越高,算法性能越好,其定义如式(16)所示:

其中,pprecision等于正确检测的异常实例与总的异常实例数之比,precall等于正确检测的异常实例与总的数据实例之比。
此外,引用文献[12]的数据集,包括温度、湿度、电波和CO24 项样本数据。
3.2 TPR 和FPR 性 能 分 析

图4 TPR 性能
图4、 图5 分别显示了4 项数据的TPR 和FPR。 由图4 可知,提出的BSP-AD 算法对二氧化碳、电波、温度和湿度4 项数据具有较高的TPR,这4 项的数据的TPR率分别达到0.93、0.79、1.00、1.00, 优于IDLO 和MAES算法[13]。
其中IDLO 算法对TPR 较低,其对二氧化碳、电波、温度和湿度4 项数据的TPR 分别为0.01、0.01、1 和0.092。 且IDLO 算法对数据类型较敏感。
图5 显示了BSP-AD、IDLO 和MAES 对4 项数据的FPR 性能。 相比于IDLO 和MAES,提出的BSP-AD 算法的FPR 最低,低于0.1;而IDLO 和MAES 算法的FPR 相近,且较高,例如,IDLO 算法对湿度样本数据的FPR 达到0.51。这些数据表明,BSP-AD 算法能够有效地检测异常数据,相比于IDLO 和MAES 算法,更能控制FPR[14-15]。

图5 FPR 性能
3.3 F1S 性能
图6 显示了BSP-AD、IDLO 和MAES 算法对4 类数据的F1S 分数。 从图5 可知,BSP-AD 算法的F1S 最高,且远高于IDLO 和MAES 算法。 例如, 在温度数据时,BSP-AD 的F1S 达 到1,而IDLO 和MAES 算 法 的F1S 分别只有0.38 和0.58。

图6 F1S 的性能
3.4 计算成本和存储成本的性能
考虑到节点属于微型节点,计算和存储能力有限。因此,异常检测算法应具有低的复杂度和小的存储成本。而BSP 树能够处理大量的数据,甚至是动态的数据流。 而IDLO 算法仅能处理静态数据,并且计算成本高。
本文提出的BSP-AD 算法采用了BSP 树,它的计算成本和存储成本与MAES 算法相似。 BSP-AD 算法的计算成本为O(t×h(logn+Ψ))。 而IDLO 算法的计算成本约为O(r×n2),其中r 为邻居数,n 为数据实例的个数。
此外,BSP-AD 算法无需计算距离或者密度测量,并控制了训练树的个数,进而降低了存储成本。 因此,BSP-AD 算法的存储成本为O(t×h×Ψ),而IDLO 算法的存储成本为O(n)。
4 结论
本文针对无线传感网络中的异常数据检测问题,提出基于二叉空间划分的异常数据检测BSP-AD 算法。BSP-AD 算法依据质量测量,并利用BSP 树训练和测试数据。 仿真结果表明,提出的BSP-AD 算法以较低的计算成本和存储成本,获取高的检测精度。后期研究中,将利用不同节点间所感测的数据间的时空-相关性,进一步提高检测精度。
