基于EKF 算法的锂电池SOC 估算策略
2021-04-02崔耕韬江卫华
崔耕韬,江卫华,涂 炜
(武汉工程大学 电气信息学院,湖北 武汉443000)
0 引言
自20 世纪90 年代以来,锂离子电池以其高能量密度和优良的充放电性能而受到人们的关注,它也从铅酸电池和镍镉电池中脱颖而出, 成为大量应用于各种微型、小型电子产品和电动车中的储能装置。因此,对于锂电池的研究应该先建立其模型,进行混合动力脉冲能力特性(Hybrid PulsePower Characteristic,HPPC)测试,分析其充放电特性。
当前,有多种经典的电池模型:理想等效模型中各参数均为不变量, 因此精度较低;Thevenin 模型增加了电池极化的影响,但不能反映各参数与荷电状态(State of Charge,SOC)之 间 的 关 系[1-3];PNGV 模 型 对Thevenin 模 型进行了改进,但精度仍较低;RC 模型能反映电池内阻、电流对SOC 的影响,具有较好的动静态特性。
目前,SOC 的估算主要有开路电压测量法、 电量累积法、电化学积分法等[4-5],而卡尔曼滤波算法与其他方法相比具有更高的估算精度,且可以修正系统初始误差,有效抑制系统噪声,因此常用于估算电池的SOC。本文提出一种扩展卡尔曼滤波算法,并进行建模仿真,具有很高的精度。
1 锂离子电池模型
本次实验采用的是二阶RC 模型,如图1 所示,用RΩ表示欧姆内阻,用Rd和Cd分别表示电化学极化内阻、电容;用Rk和Ck分别表示浓差极化电阻、电容;Ud是Rd和Cd两端电压,Uk是Rk和Ck两端电压,Uoc是电池开路电压,U 为电池端电压[6-7]。 则由戴维南定理可以得到以下公式:

图1 二阶RC 电池模型

式中,I 代表了电池电流,f(soc,t)代表了开路电压与SOC之间的关系。 进一步可得到锂电池仿真的方程式:
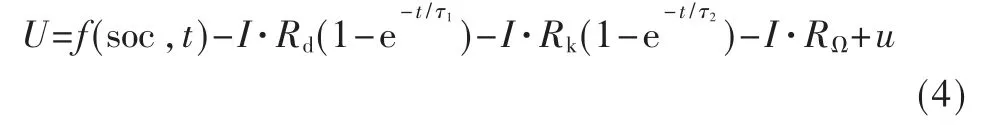
式 中, 时 间 常 数τ1=Rd·Cd,τ2=Rk·Ck,u 是 计 算 中 产 生 的测量噪声[8-9]。
2 锂离子电池充放电实验
2.1 电池的混合功率脉冲特性
HPPC 试验可以测试电池的脉冲能力以及充放电性能,一方面主要用来计算电池内阻,另一方面可以反映SOC 与电池放电能力、回馈脉冲能力之间的关系。如图2 所示,在限压5.2 V 时,用1 C 电流进行HPPC 充电和放电,从0%SOC 每次充电10%SOC~100%SOC,中间静置电池1 h,使端电压恢复至接近开路电压;后同样从100%SOC 每次放电10%SOC~0%SOC,以探索如何用电池SOC 表示开路电压和内阻。

图2 脉冲电流充放电曲线
图3 是电池充放电时的SOC-Uoc曲线,反映了SOC与开路电压之间的关系,曲线可以分成三部分。 总体上,SOC与电压呈非线性关系,且Uoc随SOC 的增大而增大;在0%SOC ~10%SOC 内,电池开路电压急剧增大,之后经历一段平稳缓慢上升的过程; 在最后90%SOC~100%SOC时,电压又较快上升。 可见在曲线的前段和末段电压对SOC 的敏感性高,曲线的中段SOC 对电压的敏感性高。
2.2 电池模型的参数辨识
在脉冲放电中,电压首先会急剧下降,这一点的电压差是由欧姆内阻引起的。 欧姆内阻可以描述为:

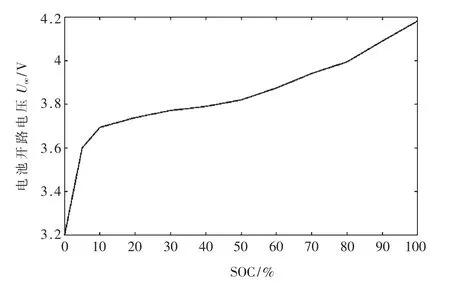
图3 电池充放电时SOC-Uoc 曲线
式中,ΔU1表示电池充电时急剧变化电压差,ΔU2表示电池放电时急剧变化电压差,I 表示脉冲电流。 由于电池的极化现象,欧姆内阻实际上也是变化的。
通过实验数据确定了RC 模型在充放电周期内的各项参数,并记录不同的SOC 点下的不同参数,然后用最小二乘法进行曲线拟合,最后用查表法将电池各个参数应用于模型。 根据图3,取长时间放置的电池的端电压作为Uoc,参考文献[10]、[11],利用1stOpt 软件,拟合得到了电池荷电状态与Uoc之间的关系。 需要指出的是SOC 的最高项次数越高,拟合精度就越高,本次拟合最高次数为8,SOC∈[0,1],用X 表示SOC,有:

图4 是锂电池在充放电中极化内阻随SOC 的变化过程图,电池的内阻会随着SOC 的减小而波动增加。 这是因为电池的内部发生着化学反应,导致电池中的材料变形,导体和电极的腐蚀,并使电解质减少,从而导致内阻的增加。
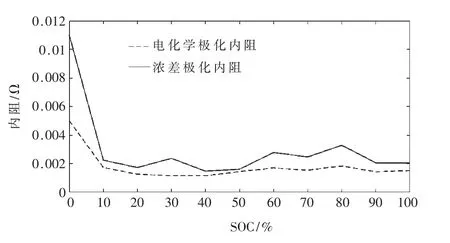
图4 充放电中极化内阻-Uoc 曲线
由图4,用SOC 表示Rd和Rk的函数关系式,SOC∈[0,1],有:

3 扩展卡尔曼滤波算法
3.1 扩展卡尔曼滤波原理
卡尔曼滤波的核心思想是利用系统观测到的输入数据和输出数据,对锂电池的真实状态作最小均方差的最优状态估计。它利用前一个值的估计值和实时测量值对下一个值进行估计,得到系统实时状态,并过滤掉观测数据中的噪声和干扰。而卡尔曼滤波仅适用于对线性系统的估计,对于锂离子电池的SOC 预测需要用到扩展卡尔曼滤波算法。 对于离散时间非线性系统,有:

式中,F(X,U)和H(X,U)为非线性函数,X 表示状态量,U 表示控制量,Z 表示观测量,W 和V 分别表示过程噪声和测量噪声[12]。 在EFK 中,通过一阶泰勒展开式对其线性化表示:


图5 扩展卡尔曼滤波结构图
3.2 扩展卡尔曼滤波与SOC
扩展卡尔曼滤波(Extended Kalman Filter,EKF)根据上一时刻的状态估计值和误差协方差对当前状态进行先验估计,得出先验估计值,再根据最新测量值对其校正,得出后验估计值[13-14]。 结合二阶RC 电池模型式(1)、式(2)、式(4),可得到离散化状态模型:

式 中,UΩ是欧姆内阻RΩ两端的电压,I 是电流,Uoc(SOC(k))是随k 时刻SOC 值变化的电池开路电压值,ΔT 是采样时间,Q 是电池容量,η 是库伦系数,k 和k-1 代表时刻。
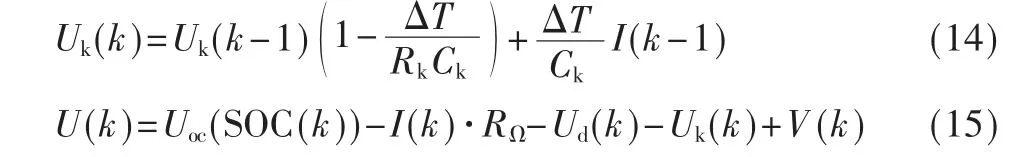
4 锂电池SOC 估算仿真与实验
本文根据EKF 原理和相关公式以及电池的参数,建立了SOC 估算模型。 输入数据后,将用库伦计数法算得的SOC 与用EKF 算得的SOC 相比较[15]。 为检验模型的精确度,在MATLAB 的Simulink 模块下进行了仿真,使用的是标称电压3.7 V、标称容量2.6 Ah 的锂电池,实验条件为25 ℃。
图6 所示是SOC 估算图,图6(a)是在脉冲电流下SOC 随放电、充电时间而改变的曲线,SOC 初始值为1;图6(b)是在恒流放电下的SOC 随时间而改变的曲线,SOC 初始值为0.9。 图7 验证了在恒流放电时估算模型与电池实际荷电状态之间的误差。
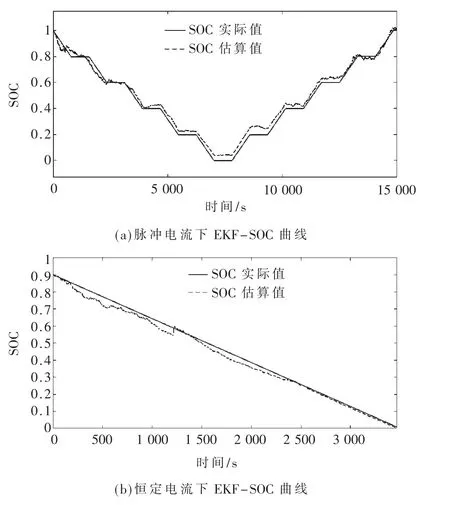
图6 EKF-SOC 估算曲线与实际SOC 曲线
图6 将不同电流下的SOC 估算值与SOC 实际值进行了对比,图6(a)放电780 s,静置780 s,每次放电量为20%SOC;图6(b)恒流放电3 500 s。图6(a)误差比图6(b)误差略大,但在合理范围之内,表明改变电流会对SOC估算产生影响。

图7 SOC 估算误差曲线
图7 所示表明此模型的估算误差大多趋于[-0.04,0.01],平均误差为2.1%,最大误差仅为5.7%,且在低于30%SOC 时,估算误差显著降低。 这验证了模型具有较高精度,且可以显著抑制噪声。 但此模型未考虑温度对电池SOC 估算的影响,同时改变电流大小对估算精度影响较大,因此模型可以继续优化改进。
5 结论
本文利用二阶RC 电路模型来捕获锂电池的电特性,通过混合动力脉冲能力测试对电池参数进行辨识,探索了电池SOC 与开路电压、内阻之间的关系。 在此基础上,提出了一种基于扩展卡尔曼滤波算法(EKF)的SOC 估算法。 建立仿真模型并进行实验后,验证表明模型的误差值在2.1%左右,与一般的SOC 估算法相比可明显提高精度。
