基于Matlab GUI“数字信号处理”实验平台设计

马月红， 孙晓云， 刘素艳

(石家庄铁道大学 电气与电子工程学院， 河北 石家庄 050001)

0 引言

随着通信科技方面的发展，以数字信号处理为基础的问题随处都在[1]。“数字信号处理”课程是通信工程专业的一门重要课程，其理论严谨抽象、系统性很强，难于理解。其基础性的知识包括：一些基本概念、离散数字信号处理的各个域的相关分析、系统函数和状态变量的分析等等。其中，卷积、傅里叶变换的计算以及一些公式定理的证明过程的工作量过于庞大且繁琐。这不仅仅增加了学生学习的难度，更是消磨了学生学习的热情。而且由于教学的部分局限性教师们很难将这些书本上的基础性知识让学生牢固掌握。

因此本文将Matlab仿真技术和GUI界面设计引入到该课程的教学实践过程中，开发了可视化的“数字信号处理”虚拟实验平台，通过一系列的仿真，实现了对信号生成模块(单位冲激序列、指数序列等六个序列)、模拟信号抽样模块、傅里叶变换模块(离散信号与周期信号)、卷积分模块以及FFT的实现与应用模块，可以让学生更加直观地看到原理展示从而进一步帮助他们理解和体会抽象难懂的内容，以此提高学生们的学习兴趣。

Matlab GUI凭借其独特的图形化编程优势，不仅能方便学生对理论知识的理解，还能增强学生的实验操作能力[2]。而本系统作为一个帮助教师教学的手段，它的主要作用就是通过将课件与Matlab的图形和动态演示在课堂上结合起来，使得教师的课堂教学更加生动、直观，让学生不再对该课程仅仅只有枯燥难懂的感觉，有利于学生们对数字信号处理以及通信的学习兴趣的提高，从而提高整个学习的教学效果。

1 系统整体设计

系统总体设计中，以自顶向下方式进行界面布局设计，以引导界面、主界面作为设计前提，在此基础上开展其他子界面设计。其中的子界面包括序列信号产生 (单位脉冲序列、指数序等) 、模拟信号抽样、卷积和、傅里叶变换 (离散信号与周期信号) 、FFT的实现以及滤波器设计。当用户完成对每个子系统的设计后，就可以开始着手创立一个主函数，通过回调函数来实现主系统与子系统之间的功能传递。系统的结构如图1所示。

图1 系统结构

系统具体主界面如图2所示。在新建窗口中拖入若干个静态文本框和若干个按钮，设置静态文本的String为“基于Matlab GUI的数字信号处理实验设计”，依次设置另外六个静态文本框String为“实验一基本信号的产生”、“实验二信号抽样理论”、“实验三傅里叶变换(DFT)”、“实验四卷积和”、“实验五快速傅里叶变换(FFT)及其应用”，点击每个实验后点击确认进入相应的的实验子界面。主界面设计完成后的内容实现如图所示。为了美化实验平台总界面作者加入了三个信号图样。

图2 主程序前面板

根据设计好的系统结构图，设置各数字信号处理实验模块，一共设计了5个实验模块，结合Matlab GUI的软件特点设计各个模块，完善前面板及程序框图，设计合理的参数。为了方便学生使用，尽量将本虚拟实验平台设计的像实验室中的实验箱一样，在一个界面上就能调用各个子实验模块，因此需要设计一个主界面，通过这个主界面实现模块之间的相互跳转，运行并显示各子模块的前面板、能够进行参数调整、并能停止实验返回主界面。

前面板是操作界面，为了方便用户使用，尽量把布局设计的像实验室中的实验箱一样，对模块进行分类，排版，并加入一些修饰元素，使其看上去简洁明了，更方便学生操作和使用。

2 系统关键模块设计与实现

2.1 基本信号生成设计与实现

利用Matlab GUI的软件特色，可以实现对波形信号的可视化操作，并能够改变信号的一些控制量来实现对波形信号的控制，在总界面其相应的位置编写总界面跳转到子界面的实现函数，如图3所示为实验一信号生产的子界面。

图3 基本信号生成程序框图

前面板分为输入和显示两大部分，输入部分可以选择信号的类型、对信号频率、相位等进行设置。显示部分是时域信号波形图。输出所设参数的对应输出时域波形。并添加了布尔停止控件，点击停止按钮便能停止实验。根据设置好序列参数，生成常用序列，以生成的单位阶跃序列和指数序列为例，如图4所示。

2.2 模拟信号抽样设计与实现

从以往的学习中可以得到：当一个时间连续信号f(t)的频带限制在(0，fn)内，当以时间间隔T≤2/(2fm)(fm为连续信号的最高频率)对这个连续信号f(t)进行抽样时，那么这个时间连续信号就可以根据那些抽样值被完全恢复出来。或者说存在一个，当它频谱中的最高频率小于等于fn的时候，这个连续信号f(t)从性质来看，肯定是一个周期信号。可以继续假设，当抽样频率fs≥2fh时，由抽样定理可以知道，原来的连续信号的全部信息就都会被抽样后的信号所包含进去，并且不可能出现混叠现象。当在后面需要原来的连续信号时，可以根据这些抽样信号的样本值来还原出原始信号。根据这一特性，可以完成信号的DA转换与AD转换。由上可以看出，程序中分别给出了参数的范围和彼此之间的关系，这样在用户在使用实验平台系统时便可手动调节Ts的大小，这时其余参数值都会随着Ts的值发生改变。从而在图像上给出直观的变现。抽样示意图和抽样后频谱，如图5所示。

图5 抽样理论图

通过对抽样周期大小的改变可以看到抽样定理的三种情况：临界抽样、不发生混叠、发生混叠。通过图像直观的观察可以清楚地看到抽样定理的内涵，并对抽样的过程、结果都有了更加深刻的理解。

2.3 离散傅里叶变换设计与实现

DFT就是对一个离散信号进行傅里叶变换，这样信号就从时域信号变换为频域信号，对频域信号可以进行幅度和相位分析。Matlab中有两种计算傅里叶变换的方法:①利用符号进行运算的方法:在Matlab的Symbolic Math Toolbox提供了傅里叶变换函数(fourier)，F=fourier(f)作为符号函数f通过此变换式，就可以得到其傅里叶变换；②利用数字进行计算的方法:要求傅里叶变换时所需信号必须是时限信号，也就是说，当时间∣t∣大于给定的某个时间时，其值将会衰减为零或近乎为零，计算机只能处理有限大小和有限数量的数。用户可以通过设置不同的序列来进行傅里叶变换。结果如图6所示。

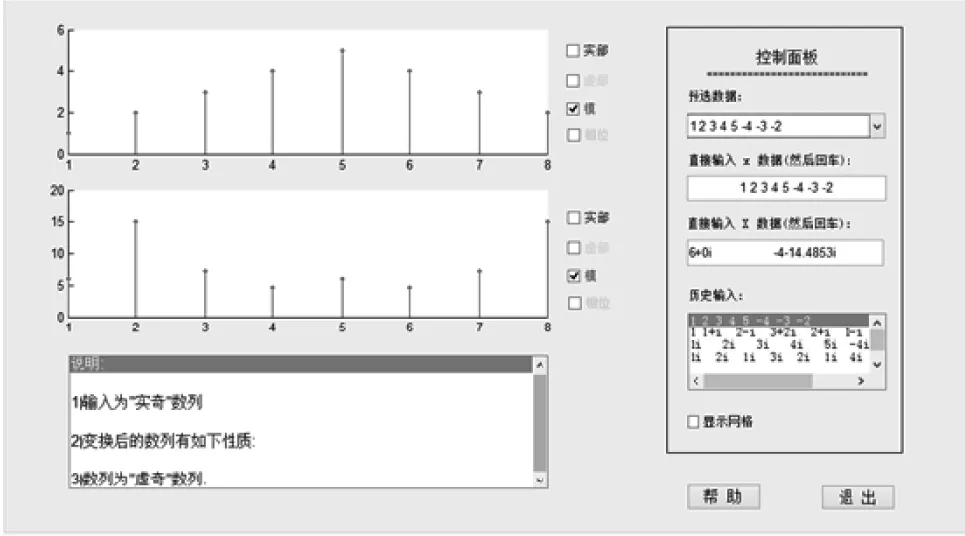
图6 离散傅里叶变换面板

2.4 卷积和设计与实现

在学习中为了计算LTI离散系统零状态响应以及离散信号的分解，一般采用的是卷积运算，并且它是解决上述问题的基本工具。

卷积模块，一般包括两个模块：离散卷积和连续卷积，在离散卷积部分，由于序列处于无限长状态，无法在Matlab直接应用下进行卷积计算，但Matlab中的内部函数conv，在计算卷积方面可发挥重要作用。对于连续卷积，也需借助该函数完成连续信号的计算。实验中设置的参数：

x=str2num(get(handles。edit_x，'String'));nx=0:1:length(x)-1;

h=str2num(get(handles。edit_h，'String'));nh=0:1:length(h)-1;

y=conv(x，h);ny=0:1:length(y)-1;

运行结果如图7所示：

图7 卷积积分面板

2.5 FFT变换及应用设计与实现

当遇到两个时域特性相同的信号，这两个信号不一定就完全相同，此时就需要对信号进行频域分析，通过傅里叶变换将时域信号变换为频域信号，进而分析信号的频率和相位特性。传统的离散傅里叶变换的算法过程过于繁琐，计算量庞大，因此引进了一种快速算法，即FFT变换，在本质上与傅里叶变换并无差异，只是通过一些方法巧妙地减少了运算量。

FFT算法一般分为两类，一类就是按偶奇来区分并对频域信号序列进行排序的按频率抽取。另一类就是按奇偶来区别并对时域信号序列进行排列的按时间抽取。它们的计算中都借助了 的周期性和对称性这两个特点。这样就可以把FFT计算分成若干步进行，计算效率大为提高。

假设输入信号具有N个抽样点，则输入信号就会有N个原始数 ，可以由以前的学习中得知在经过一级的计算后就会产生新的N个数据 。根据归纳演绎法，最后会得到x(k)= =X(k)，可以发现在一级级的计算的过程中，作为每个蝶形运算的输出数据的存放位置就是原来的输入数据的存放位置，这就是平时运算中所说的“即位计算”，这样可以节省大量存放中间数据的寄存器。

而每一级的蝶形运算中加权系数是不同的，它是随迭代级数成倍增加。如图8是一个蝴蝶运算的基本运算单元，可以看出每一级运算中输入数据与输出数据之间加权系数的关系。并且每一个输入数据其实就是上一级的输出数据，而每一级的输出数据就是下一级的输入数据。由此我们可以得到蝴蝶运算的加权系数的关系：每级迭代的不同加权系数的数目比前一级迭代增加一倍；跨度间隔也增大一倍。

N=8的蝶形运算示意图如图9所示，使用者在使用系统时可以通过修改序列值来进行不同序列的FFT运算。与用户在传统的教学方法有很大的不同并且十分的快捷。这大大的节省了教育工作者的教学时长，给学生减少繁琐枯燥的运算过程，增加了学生的学习兴趣。

3 结语

本课题设计是针对国内“数字信号处理”课程的教学现状进行的课题设计。(马月红等文)

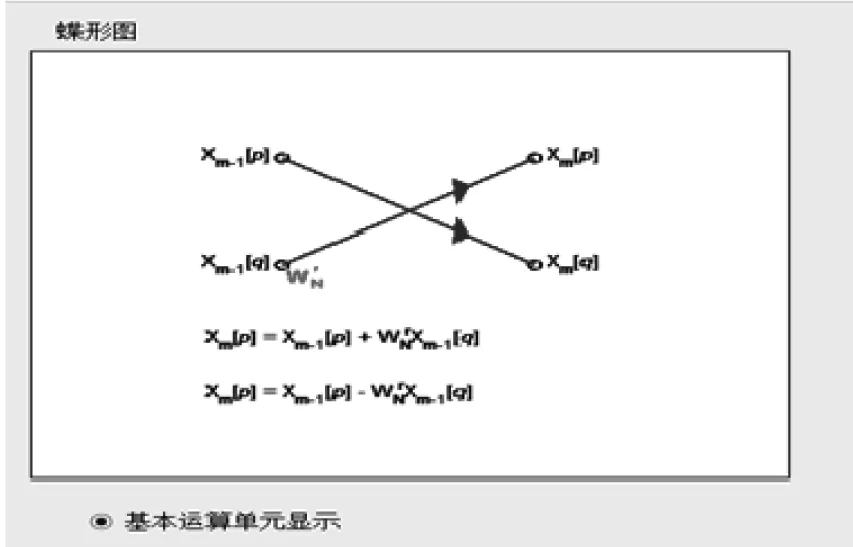
图8 FFT基本运算单元

图9 蝶形运算示意图

Matlab GUI软件强大的功能使得该虚拟实验平台不仅能够降低教师的教学难度，丰富教学内容，对学生的学习过程也有很大的帮助，通过流程图的形式，帮助学生理解相关理论，并达到实验操作的基本要求。