用耦合模原理分析RLC串联电路
2021-04-02陈希有李冠林董维杰
陈希有, 齐 琛, 李冠林, 董维杰
(大连理工大学 电气工程学院, 辽宁 大连,116023)
0 引言
在电网络或其他系统中,广泛存在着能量的往返传递现象。例如,电场能量与磁场能量、动能与势能、一个系统的能量与另一个系统的能量等,它们可以振荡性地相互传递和转换。这种传递和转换物理上叫做模式耦合。着眼于这种模式耦合的分析方法是一种叫做耦合模原理的方法。
早在1963年以前就有专门介绍耦合模原理的著作[1]。耦合模已在行波管、回波振荡器、参量放大器、均匀传输线中得到不同程度的应用。耦合模原理为认识这类具有模式耦合的系统提供了有效的统一方法。
近些年,由于无线电能传输技术的研究热潮,以及MIT学者在他们的研究文献中使用了耦合模原理,使得耦合模又重新被人们所关注[2,3]。所谓无线电能传输,就是不通过物理接触或电气接触,借助某种物理场或波,在一定距离内实现电能从发射系统到接收系统的传递。由于电磁现象的固有规律,在系统工作过程中,能量是往返传递的。因此无线电能传输系统刚好符合耦合模的研究对象。
本文结合笔者在无线电能传输技术中的研究,以及“电路理论”课程教学,以简单的RLC串联电路为例,介绍了用耦合模原理分析电路的方法和特点。如能将耦合模原理应用到更多的电路分析内容,定会给电路理论带来一股别样气息。
1 耦合模的电路定义
在含有电容与电感的电路中,如图1所示,由电容电压和电感电流按下式组成的复数形式的状态变量称为耦合模,即
(1)

图1 含有电容和电感的电路
由耦合模的上述定义,不难总结出耦合模的下列性质:
(1)耦合模是随时间变化的复数。
(3)耦合模绝对值的平方等于它所联系的电场能量与磁场能量的总和,即
(2)
(4)由耦合模按照下式可以分别求得电容电压和电感电流,即
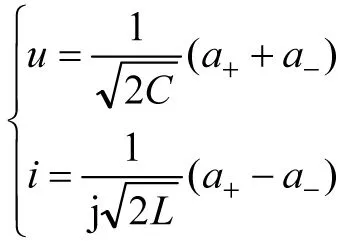
(3)
(5)由耦合模可以分别求得电场能量和磁场能量,即

(4)
(6)以下各式也可作为耦合模的定义:
(5)
(6)
(7)
当使用不同的定义时,由耦合模计算电容电压、电感电流,以及元件和电路储能时,计算公式是不同的,但都不难从耦合模的定义推导出相应的计算公式。
所谓耦合模分析,就是以耦合模为状态变量,依据电路定律列写状态方程并求解。下面用具体电路说明用耦合模概念分析电路的方法和特点。
2 理想LC回路的零输入响应
电路如图2所示。以耦合模为状态变量,列写电路方程的一般步骤如下:
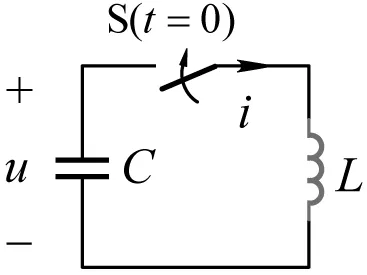
图2 理想LC回路
(1)依据基尔霍夫定律,对电路列写状态方程得
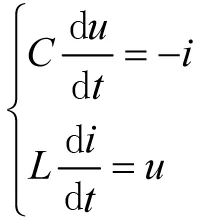
(8)
(2)将式(3)代入式(8),消去电容电压和电感电流得
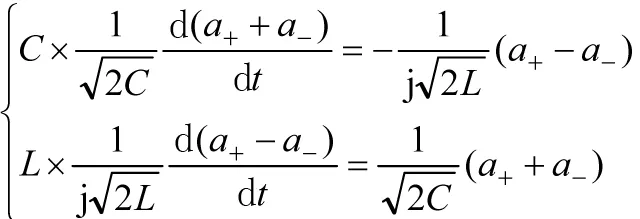
(9)
(3)整理后得到以耦合模为状态变量的状态方程
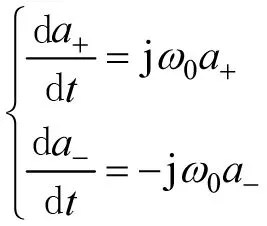
(10)
其中 表示电路的固有角频率,即
(11)
方程(10)就是图2电路的耦合模方程。式中的两个方程不是联立关系,可以很容易地单独求解,得到

(12)
式中A+、A-由初始条件确定,即
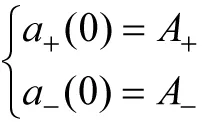
(13)
而a+(0)、a-(0)又由电容电压和电感电流的初值,并通过耦合模的定义来计算。例如,设u(0)=U,i(0)=0,则由耦合模定义即式(1)得
(14)
代入式(12)得耦合模的零输入响应:

(15)
可见a±分别代表了两个旋转方向相反的矢量,如图3所示。矢量长度相等且为常量,即
(16)
因为耦合模绝对值的平方就是总能量,所以长度为常量意味着在时间进程中,电路的总能量保持不变,这与理想LC回路的无损性质是一致的。
从电路课程可知,对于图2所示的理想LC回路,开关接通后,电路立即按正弦规律变化,并且表达式为

(17)
由式(17)及耦合模的定义式(1),也可得到式(15)的耦合模响应,即

(18)
由此验证了式(15)的耦合模响应。
如果按式(2)计算电路的总能量,结果是
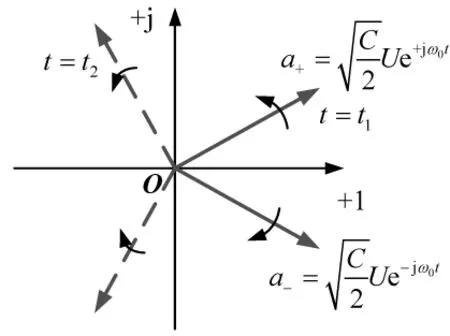
图3 理想LC回路中耦合模的几何意义

(19)
3 RLC串联电路的零输入响应
电路如图4所示,将固有角频率和阻尼因子分别记作:
(20)
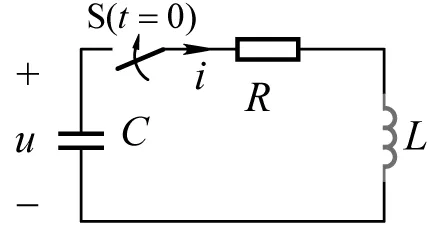
图4 RLC串联电路
按照与图2相似的分析步骤,先依据基尔霍夫定律列写状态方程:
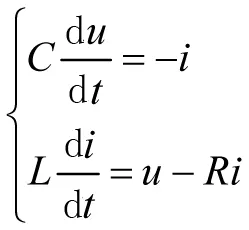
(21)
将式(3)代入式(21),整理后得到关于耦合模的齐次状态方程,即

(22)
利用耦合模可以分析电阻消耗的功率,对此有多种途径。
(1)利用耦合模求出电流,然后代入电阻功率公式,即
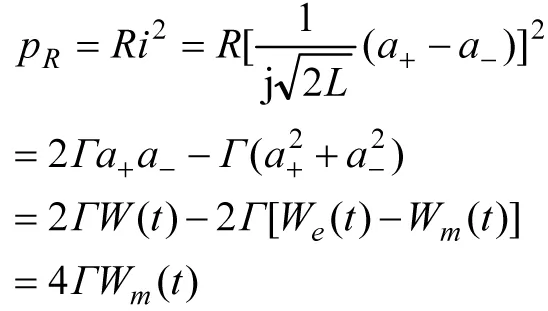
(23)
(2)利用电阻消耗的功率必然等于系统总能量随时间减少的速率,得
(24)

pR=Ri2=R[(2/L)Wm(t)]=4ΓWm(t)
可见电阻消耗能量的速率与磁场能量成正比,这是因为二者都正比于电流的平方。
为求解耦合模方程(22),可以利用拉普拉斯变换。在“自动控制原理”等课程中已经给出了求解齐次状态方程的公式,即

(25)
下面按照公式(25)给出主要计算结果。
系数矩阵行列式为

(26)
特征根为
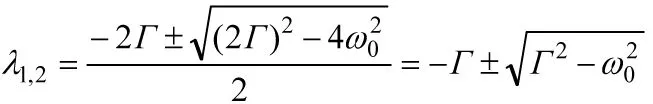
(27)
逆矩阵为

(28)
其中各部分分式的系数为
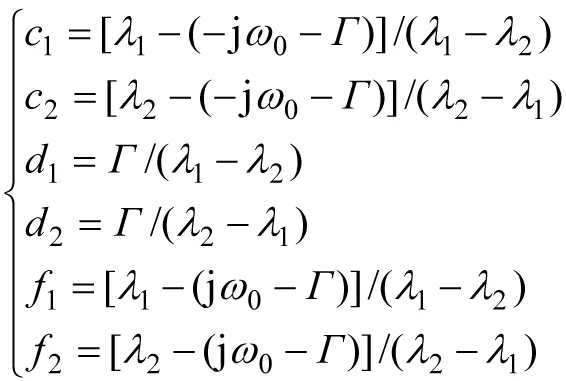
(29)
拉普拉斯反变换为

(30)
根据公式(25)得耦合模方程即式(22)的解为

(31)
根据耦合模的解答,进一步可以求得电场能量We(t)与磁场能量Wm(t),及电路总能量W(t)随时间的变化规律。图5是根据式(31)和式(4),并通过数值计算获得的响应波形,它们与用传统的电路分析方法获得的波形完全一致。

图5 用耦合模计算的电路储能
由于方程组(22)的两个方程中存在耦合项,即第一个方程中的Γα-和第二个方程中Γα+,因此需要联立求解,求解过程略显复杂。然而,对某些问题,这些耦合项的作用相对其他项很小,因此可以忽略它们。这样就得到相对简单的状态方程,即

(32)
振荡频率足够高,且R很小时可以这样忽略。对无耦合项的齐次方程(32),很容易求得解答为

(33)

由耦合模的解答即式(33),可以求得系统总能量的近似变化规律,
W(t)=a+a-=A+A-e-2Γt=W(0)e-2Γt
(34)
总能量近似按指数规律减少,指数规律的时间常数为1/(2Γ)=L/R。用式(34)表示的能量随时间的近似变化规律如图6所示。虽然它与精确计算结果存在误差,但由于忽略了耦合项,使得耦合模方程的求解变得极其容易。
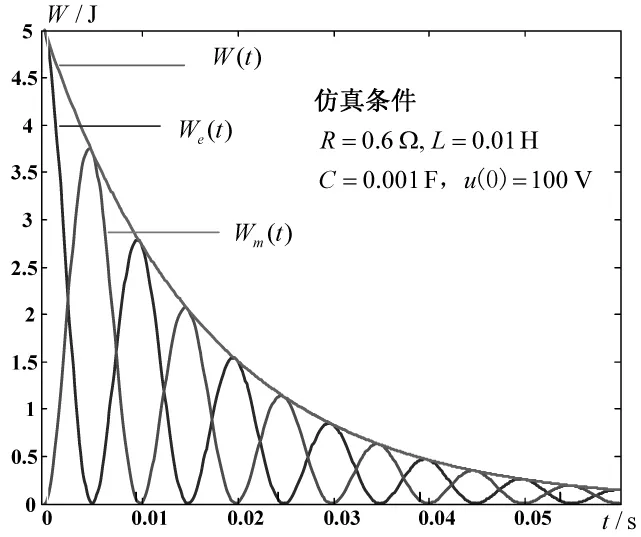
图6 用简化耦合模方程计算的电路储能
4 RLC串联电路的正弦稳态响应
图7是正弦激励下的RLC串联电路。根据基尔霍夫定律列出状态方程,即
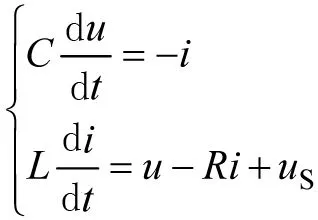
(35)
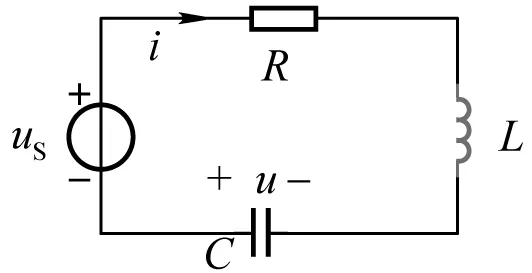
图7 正弦电压激励下的RLC串联电路
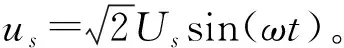
(36)
将耦合模的性质即式(2)及式(36),代入方程(35),并利用与式(20)相同的定义,得到正弦激励下RLC串联电路的耦合模方程,写成矩阵形式就是

(37)
这是关于耦合模的非齐次状态方程。为求其正弦稳态解,即微分方程的一个特解,可使用叠加定理按如下步骤进行。
(1)ejωt对应项单独作用
此时耦合模方程是
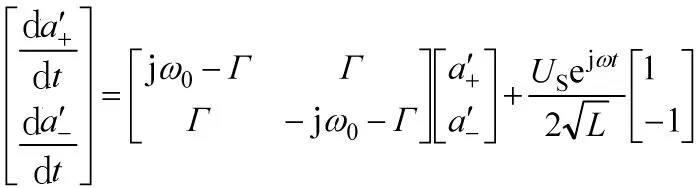
(38)
由于激励是ejωt形式的函数,根据微分方程性质,它的特解也具有相同的形式,因此令
(39)
其中B'和D'是需要待定的系数。待定方法是,将式(39)代入方程(38),约掉等号两边的ejωt项后再简单整理得到
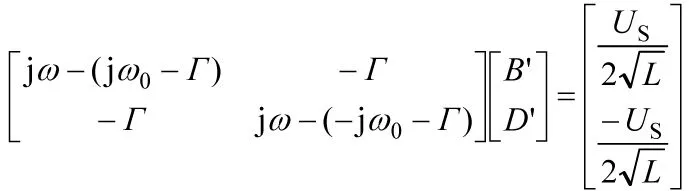
(40)
下面给出求解方程(40)的主要结果。系数行列式:
(41)
代数余子式:
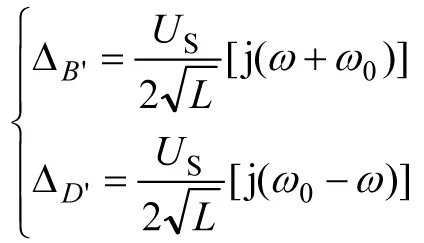
(42)
因此,待定系数为
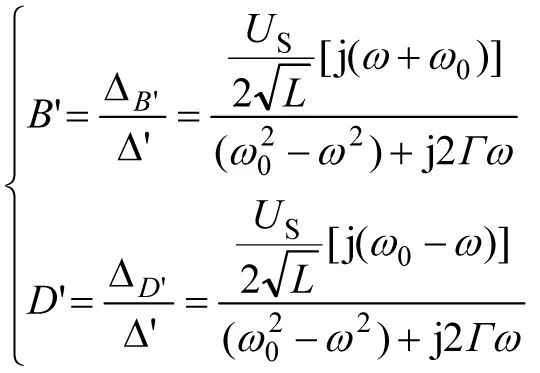
(43)
(2)e-jωt对应项单独作用
此时耦合模方程是
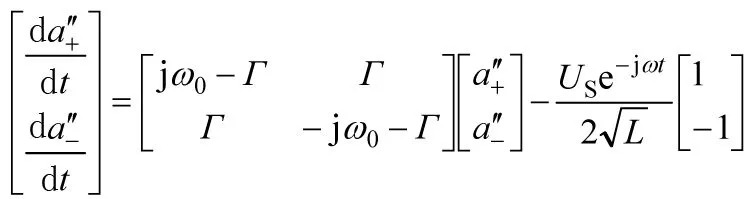
(44)
此时须令耦合模的特解
(45)
其中待定系数B"和D",可以仿照B'和D'的求解过程来得到。但由于
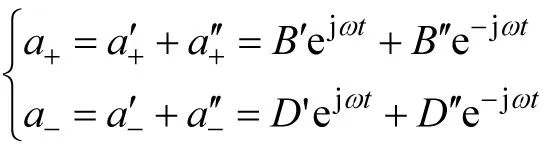
(46)
B"=D'*,D"=B'*
(47)
根据耦合模计算出电路储能的变化规律,如图8所示。计算条件是R=2Ω,L=0.01H,C=0.1mF,ω=0.8ω0。
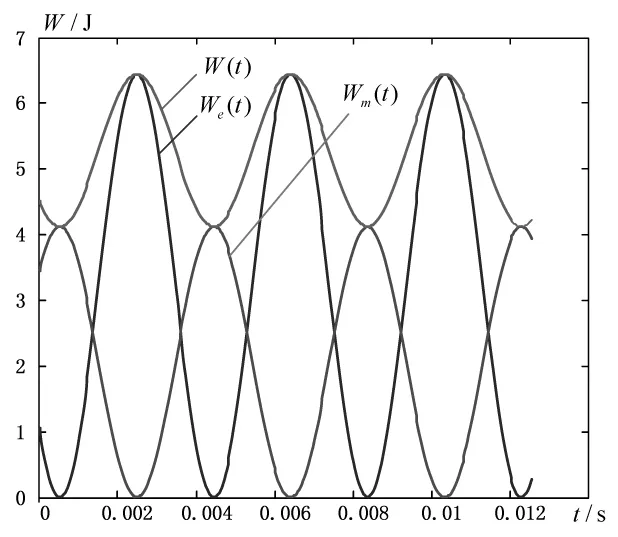
图8 RLC串联电路正弦稳态下储能变化情况
当ω=ω0,即满足谐振条件时,由电路理论早已知道,此时电场能量与磁场能量实现完全互补交换,电路总能量保持不变。这一结论也可由耦合模方程的解答得到验证。当ω=ω0时,根据式(43)和(47)可知
B"=D'*=0
(48)
此时耦合模解答中只有一个指数项,即
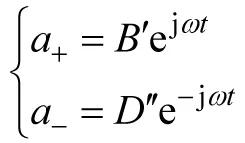
(49)
上述耦合模的绝对值平方为常量,正好符合谐振时电路总储能不随时间变化的性质。
根据耦合模计算出谐振时电路储能的变化规律,波形如图9所示。
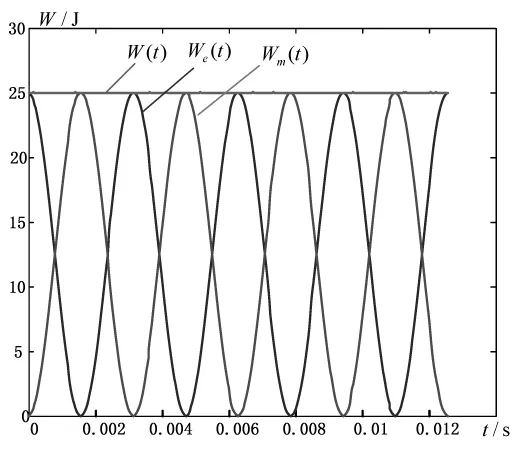
图9 谐振条件下的电路储能变化情况
在耦合模方程(37)中,由于存在耦合项,使得待定系数的求解变得比较复杂,需要求解二元联立方程。如果忽略耦合项(R很小时可以这样忽略),则可简化待定系数的计算。忽略后的耦合模方程为
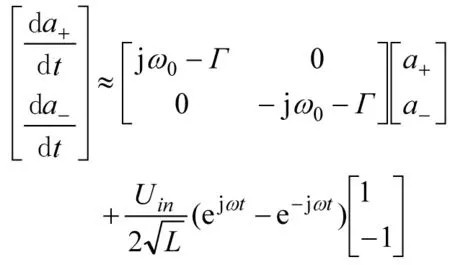
(50)
其稳态解可以令为

(51)
仍然按照叠加定理的思路确定待定系数,但无需求解联立方程,得到的待定系数分别是
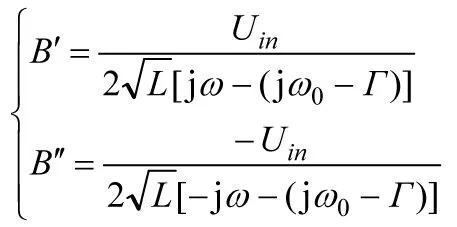
(52)
并且D'=B"*,D"=B'*
(53)
根据简化后的耦合模方程及其解答,近似计算谐振条件下电路储能的变化规律,波形如图10所示。总能量不再是常量。
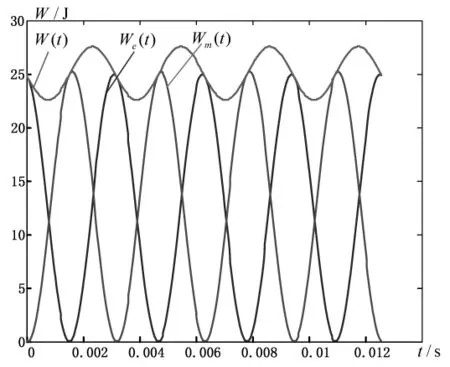
图10 谐振时电路储能的近似计算
5 结语
本文介绍了用耦合模原理分析电路的方法和特点,结论如下:
(1)本文介绍的耦合模在电路中的基本概念,以及在RLC串联电路分析中的应用。从分析RLC串联电路这个简单例子看,用耦合模分析暂态响应或正弦稳态响应,并没有表现出明显的优势。但它以复数形式的状态变量为待求量的认识问题的角度是独特的,是对电路理论的一种丰富。
(2)在分析更多储能元件的电路、含有耦合回路的电路、机电耦合系统、电热耦合系统等,还有待深入研究。
