基于工程实例的DFT教学实践与探索
2021-04-02杨玲君刘开培
王 静, 杨玲君, 刘开培
(武汉大学 电气与自动化工程学院,湖北 武汉430072)
0 引言
离散傅立叶变换DFT(Discrete Fourier Transform)是“信号与系统”课程的一个教学重点和难点,其物理意义抽象,公式表达复杂,学生掌握和应用难度大[3~4]。中国国家标准GB/T17626.7-2008和国际标准IEC61000-4-7: 2002中推荐使用DFT进行谐波检测[2]。作为电气与自动化学院学生,掌握DFT的基础基本理论,利用DFT解决实际工程问题,是学习信号与系统课程的一项基本要求,也是培养大学生创新科研能力的需要。
DFT直接在时域离散有限长序列与频域离散有限长序列之间建立一种变换关系,可以用计算机进行信号的频谱分析[1]。为了让学生更好理解DFT 的基本概念,本文首先梳理了DFT与离散傅里叶级数DFS(Discrete Fourier series)、离散时间傅里叶变换DTFT(Discrete Time Fourier Transform)之间的关系;然后引入电力系统典型的谐波分析案例,设计实践教学环节,从而加深对DFT的理解和应用。
1 DFT 理论教学环节设计
在对离散时间信号x(n)进行频谱分析时,如果x(n)是周期的,周期为N,用DFS计算频谱,其频谱是周期为N的离散频谱,如式(1)所示。
(1)
如果x(n)是非周期的,可以用DTFT计算频谱,其频谱是连续的,如式(2)所示。
(2)
DFT的定义如式(3)所示
(3)
式(3)中,x(n)是时域的离散时间信号,X(k)是x(n)的频谱,两者都是长度为N的序列。
比较式(1)和式(3),可以将DFT看作是将DFS的主值(0~N-1)抽取出来人为定义的一种变换,其目的就是为了能够对有限长序列的频谱进行计算机分析[1]。从物理概念上讲,DFS是经过严格数学推证得到的,符合实际信号特性的,因此它反映了一种客观的物理现象;而DFT却不然,因为实际物理信号中不可能存在一个时域有限、频域也有限的信号。比较式(2)和式(3),DFT可以看作是将DTFT在一个周期的等间隔取样,取样间隔为2π/N。
2 工程案例设计
随着智能电网的建设和大规模的新能源并网,越来越多的电力电子设备接入电网,在减少环境污染和增强电网功能同时也给电网带来了大量谐波。
2.1 谐波信号数学建模
(4)
式中f0=50 Hz,m表示谐波的次数。
在对谐波进行频谱分析时,首先要对谐波信号进行采样,即令t=nTs,Ts为采样间隔。采样后的信号表达式如式(5)所示。
(5)
令2πf0Ts=Ω,Ω0为数字基波频率,单位为rad。则式(5)可表示为:
(6)
本文为了说明如何用DFT计算谐波信号的频谱,并便于验证该算法的正确性,将谐波信号进行简化,假设谐波信号如图1所示,数学表达式如式(7)所示。从式(7)中可以看出,该信号包含了基波,3次谐波,5次谐波和7次谐波。
(7)

图1 谐波信号
2.2 谐波信号的离散化处理
利用DFT对谐波信号进行频谱分析,首先对谐波信号进行采样,变成离散时间信号。采样关键参数是采样频率fs和采样时长T0(采样点数N)。根据采样定理,对于带限信号,要求采样频率fs大于或等于信号最高频率的两倍[1]。在本算例中,要测量的最高次谐波为7次谐波,所以采样频率fs至少选取700Hz。如果采样频率为700Hz,采样后的谐波信号如式(8)所示,这里数字基波频率Ω0=π/7rad,采样后得到的离散信号如图2所示。
(8)
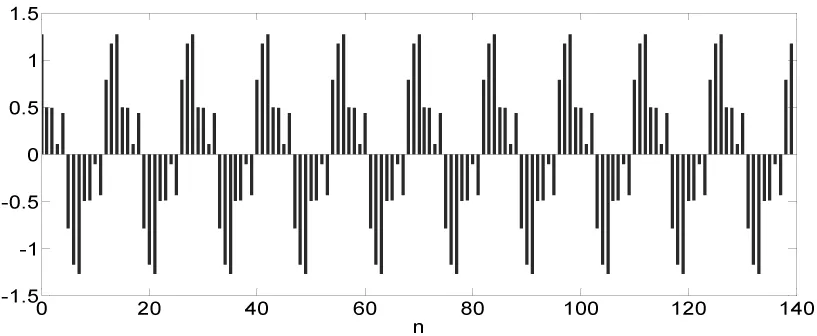
图2 采样后的谐波信号
采样时长T0(采样点数N)与离散域频率分辨率F0有关。频率分辨率F0表示应用离散傅立叶变换进行频谱分析时在频率轴上所能得到的最小频率间隔。根据文献[1]可知,采样时长T0与频率分辨率的关系如式(9)所示:
试剂及耗材:美国MO Bio公司生产的Power-Soil DNA Isolation Kit、百迈克微生物高通量测序建库试剂盒、美国BioLabs公司Phusion HF MM高保真PCR酶、德国Qiagen公司MinElute®PCR Purification Kit、美国Illumina公司Sample Preparation Kit、全式金Taq DNA Polymerase、北京华大公司的合成引物、西班牙琼脂糖Agarose、全式金Marker DL5000、Goldview Nucleic Acid Gel Stain等。
(9)
电力系统谐波是工频(50Hz)的整数倍,因此要求频率分辨率为F0≤50Hz,则采样时长T0≥0.2秒,即至少采样一个工频周波,如果采样频率为700Hz,则采样点数至少为N=T0/Ts=14。
3 基于DFT的工程案例分析
为了治理电网中的谐波污染,确保电网安全运行,快速、准确的谐波参数检测是必不可少的。基于DFT的谐波测量方法是目前最普遍的电力谐波测量方法,也是许多新的谐波测量方法的基础[5]。
3.1 DFT程序设计
DFT是为了利用计算机来实现信号的频谱计算而定义的傅立叶变换,因此程序设计是实现DFT工程应用的前提。本课程建议学生掌握公式(3)基础上用Matlab编程实现DFT的计算,程序如下。
function [Xk]=dft(x)
N=length(x);
n=0:N-1;
k=0:N-1;
Xk=0;
for n=0:N-1
Xk=Xk+(1/N)*x(n+1)*exp(-i*2*pi*k*n/N);
end
3.2 采样频率的选择
当采样频率为700Hz,采样点数为14时,计算出的频谱如图3所示。
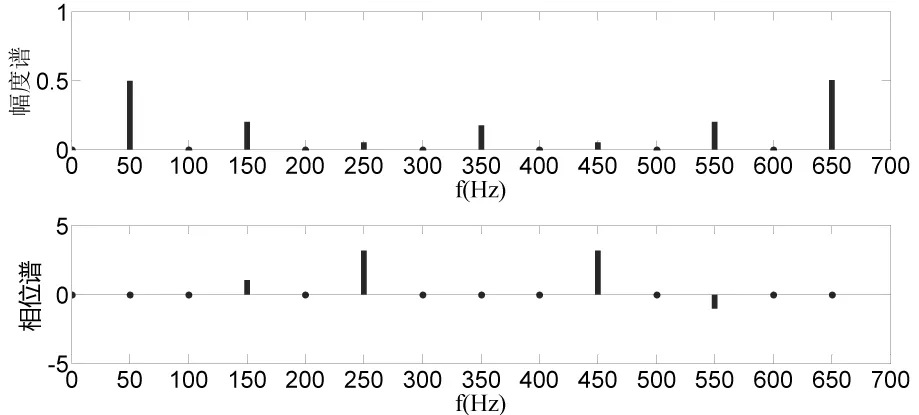
图3 采样频率为700 Hz时信号的频谱
由DFT的对称性可知,X(k)的幅值|X(k)|关于k=N/2偶对称,幅值为原信号幅值的1/2,相角关于k=N/2奇对称的,因此只需考察k=0~2/N,即频率为0~350Hz范围内的频谱分布。由图3可知,基波、3次谐波和5次谐波的计算值与理论值相同,但是7次谐波的幅值和相位有误差,产生了频谱混叠。因为谐波信号是正弦信号的叠加,正弦信号的频谱是冲激函数,因此不能将谐波信号看作是带限信号。根据文献[6],对正弦信号采样时,建议一个周期至少抽样3个点,即采样频率为正弦信号频率的3倍。因此,对于上述谐波信号,采样频率可设为1200Hz,仍然采样一个工频周期,采样24个点。由于DFT的对称性,计算所得的频谱关于600 Hz对称,只考察0~600 Hz范围内的频谱分布,频谱如图4所示。
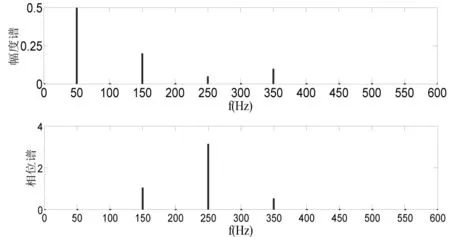
图4 采样频率为1200Hz时信号的频谱
由图4可以看出,当采样频率为1200 Hz时,用DFT计算出的频谱与理论之完全一致,没有发生频谱混叠。
本案例通过采样频率的选择,让学生对正弦信号的频谱特点、采样定理的应用范围和频谱混叠现象有了更加直观的理解。
3.3 采样时长的选择
如果采样频率仍取1200,但是采样点数取30,即采样1.25个工频周期,得到的频谱如图5所示。
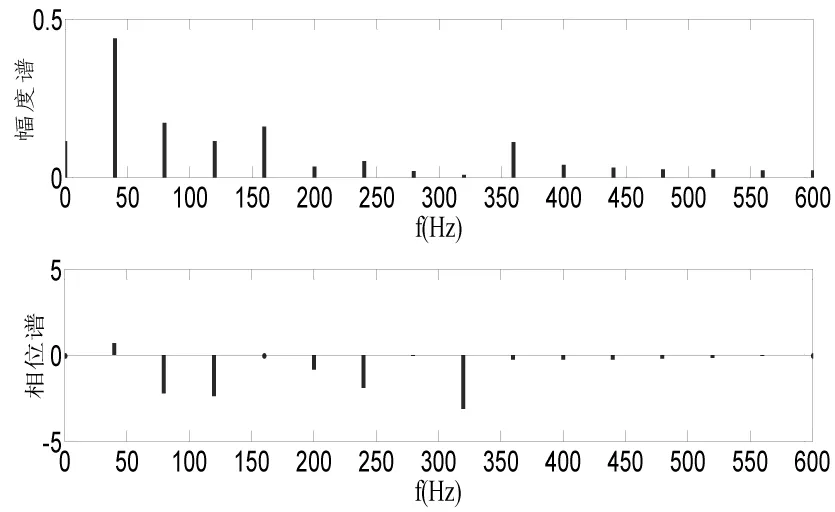
图5 非整周期采样时信号的频谱
从图5可以看出,由于对谐波信号进行非整周期采样,发生了频谱泄露。在用DFT计算频谱时,DFT具有隐含周期性[1],在本例中,采样30个点,DFT计算时认为这30点是一个周期,进行频谱计算。因此在对正弦信号采样时,一定要满足采样点数是整个周期[6]。国标GB/T17626.7-2008《电磁兼容试验和测量技术供电系统及所连设备谐波、谐间波的测量和测量仪器导则》推荐采样时长为10个周期,即0.2s,采样频率为3200Hz[2]。
本案例通过采样时长的选择,让学生对DFT隐含周期性、频谱泄露和周期信号的采样时长问题有具体的认识,起到了开阔思路的良好作用。
4 结语
本文通过在课堂理论教学中引入实际工程实例,引导学生理解和掌握DFT的基本概念,并通过应用DFT计算电力系统谐波信号的频谱,分析DFT计算过程中的参数选择问题,使学生更直观认识频谱混叠和频谱泄露现象。教学实践表明,将理论知识与工程实例相结合的授课方式,加深了学生对理论知识的理解和应用,提高了学生的学习兴趣和解决实际工程问题的能力,收到了良好的教学效果。
