列车开行方案优化中的机车交路影响研究
2021-04-02林柏梁王振宇倪少权赵伊楠
林柏梁,王振宇,倪少权,赵伊楠
(1.北京交通大学 交通运输学院, 北京 100044;2.西南交通大学 交通运输与物流学院,四川 成都 610031)
目前的货物列车开行方案优化隐含着这样一种假设:列车到达一个技术站时,若不进行解体改编作业则必有更换机车等无调作业,即默认直达列车途经技术站时必有无调作业。这种假设在蒸汽机车时代是合理的,因为蒸汽机车一般采用肩回式机车交路运行,通常每运行200~300 km就需要加煤加水换挂机车,这一距离与实际路网中相邻技术站间距比较接近,因此默认直达列车途经技术站时必有无调作业是合理的。但是在牵引动力已经取得重大进步的今天,电力机车和内燃机车已经完全取代了蒸汽机车,它们两者普遍采用循环制和半循环制机车长交路。除此之外,随着铁路网的不断完善,部分技术站间的间距较短,甚至小于机车交路的距离,这也使得列车在途经技术站时并不一定需要换挂机车。实际中,在技术站的货物列车作业类型主要有:到达解体或自编始发、无改编中转、部分改编中转和直接通过。其中到达解体和编组出发对应的是车辆的有调作业,无改编中转对应的是无调作业,部分改编中转列车主要是换挂车组作业,一般纳入分组列车的组织范围,本文暂不考虑部分改编中转列车。这里的直接通过列车是指既不进行有调作业也不进行无调作业的列车。综上分析,列车在技术站的作业模式可以归纳为:有调作业、无调作业、既不进行有调作业也不进行无调作业3种模式,而不是传统的前两类。需要说明的是,列车的无调作业通常在到发场或出发场(或直通场)上办理,包括列检、货检、换挂机车等作业。其中机车换挂作业占据了无改编中转作业的主要时间。因此,本文将列车的无改编中转作业等价为机车换挂作业,作业车站由机车交路确定,从而间接关联机车交路与无改编中转列车的内在联系。本文在研究机车交路对列车开行方案的影响时,将机车交路作为输入条件,综合考虑无调作业和有调作业对货物列车开行方案的影响。
在有关货物列车开行方案优化的研究中,文献[1]引入多商品流思想,将货物列车开行方案问题看做多商品流网络设计问题,并设计一种大规模领域搜索算法来求解。文献[2-4]将该问题看做铁路网节点能力有限的规划问题,充分考虑了路网的通过能力和运输能力,并根据所建模型的特性分别设计相应的启发式算法进行求解。文献[5]构建货物列车开行方案双层规划优化模型,上层模型是列车服务网络设计模型,下层模型在上层模型提供的网络中进行配流,并设计模拟退火算法求解。文献[6-7]构建铁路车流径路与列车编组计划整体优化的非线性模型,并设计模拟退火启发式算法进行求解。文献[8]最早发现直达列车途经技术站均存在无调作业假设缺陷,考虑机车长交路因素,提出机车长交路条件下车流组织优化模式的重构模型。文献[9-11]分别研究了分组列车和快运班列的开行方案优化问题。
综上所述,既有的关于货物列车开行方案优化的研究几乎均未考虑机车交路的影响,仅文献[8]发现直达列车途经支点站均存在无调作业假设缺陷,并提出机车长交路条件下车流组织优化模式的重构模型,由于文中模型没有对直达列车服务网络和车流有调中转地点选择进行上下层规划分离,导致模型求解的困难,故仅仅给出了模型及其分析。本文在此基础上,分离直达列车服务网络优化与改编配流,分别构造直达去向优化的上层规划模型,和针对每个备选直达方案的下层中转配流模型,通过模拟退火随机产生上层的直达去向进行迭代优化。
1 问题描述
传统的货物列车开行方案优化模型的目标函数是基于“min(集结车小时+有调作业停留车小时)”的框架,如文献[5-6]中模型的目标函数为
(1)

式(1)中第一项为货物列车的总集结费用,第二项为车流的额外改编总费用。由式(1)可知,传统模型仅考虑了直达货物列车的集结费用成本并未考虑其无调作业费用成本。目前国内直通、直达列车机车交路为400~600 km较为普遍化,而铁路网中相邻技术站间的间距一般在100~300 km,这意味着在现有背景下,若直达列车采用机车长交路,则在途经技术站时并不一定进行换挂机车等无调作业。以图1为例说明传统模型假设的局限性,假设开行F到H的直达列车,其中B站、F站、G站为机务折返段所在站,C站、E站、H站为机务段所在站,下图中绿色线段代表肩回式机车交路,蓝色线段代表循环式机车交路。
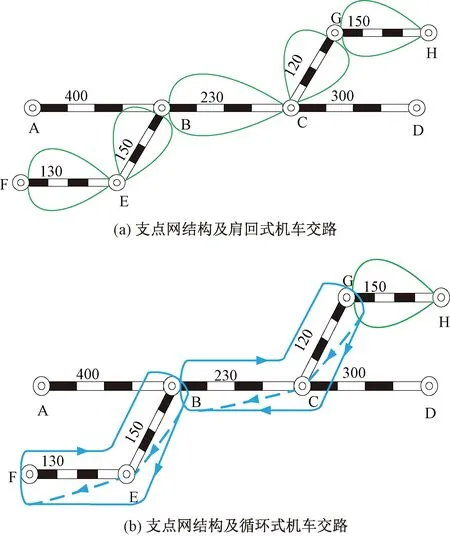
图1 传统模型(单位:km)
图1(a)中,该直达列车在各个区段均采用肩回式机车交路,即列车途经各个技术站时必会进行换挂机车等无调作业。这种情况适用于传统的基于蒸汽机车的假设,因此在货物列车开行方案优化研究时,默认直达列车在技术站必有换挂机车的无改编作业是合理的。
图1(b)中,该直达列车在F—B和B—G区间采用循环运转制机车交路,在G—H区间采用肩回式机车交路。结合图中实际情况,列车从F站出发,由于在F—B区间采用的是循环式机车交路,那么列车在途经E站时并不会停站换挂机车,而是到达B站后进行机车换挂,其原因是机车运行受到所属区段的限制。同理,列车在途经C站时也不需要换挂机车,只需要在G站进行换挂机车等无调作业,最后到达H站。综上分析,在现有背景下,直达列车在途经技术站时并不一定进行无调作业,具体作业情况受到机车交路的影响。
2 双层规划建模
2.1 模型参数及决策变量
参数符号及定义见表1。

表1 模型符号及定义
2.2 上层规划模型的构建
如果计划提供一组从i站到j站的直达列车,假设其途经的技术站有n个,则其中要办理无调作业的车站数量一般小于n,这在不同的铁路线路上有不同的方案。在数学上,这样的在途无调作业总费用为
(2)
式中:λij为编组去向i→j的日均开行列数,其值为该编组去向的日均流量与列车编成辆数之比,即
λij=Dij/mij
(3)
(4)
式中:fij为i到j的实际车流量,包括i的后方站在该站中转(在i站进行改编)形成的去往j站的车流,是一个中间变量,即
(5)
上层规划模型确定铁路网络上哪些点对之间要提供直达列车服务,可构造为
(6)

(7)
(8)
Fk≤θkCRk∀k∈S
(9)
(10)
(11)
(12)
式中:φ(Dij)为调车线数需求函数;Fk为k支点站的改编负荷量。按照文献[12],一般是200车占用一条股道。
目标函数式(6)由3部分构成,第一项为直达列车的集结车小时和途经技术站无改编通过的列车小时总成本,第二项为直达列车在途的无调作业总费用,第三项为所有支点站的车流改编费用。式(7)确保每支车流仅选择一种输送方案,即车流输送方案的唯一性。式(8)是逻辑约束,如果i站到j站的车流在k站进行改编,那么i站到k站一定开行直达列车。式(9)是关于车站解编能力的约束,即车站的解编负荷要小于车站的解编能力。式(10)是车场调车线约束,考虑到编组股道运用具有一定的灵活性,本文采用φ(Dij)=Dij/200的形式确定每个编组去向对股道的需求。即需要占用的调车线数要小于车场可用的调车线数。式(11)表明决策变量为0-1变量。
2.3 下层规划模型的构建
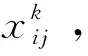
(13)
s.t.
(14)
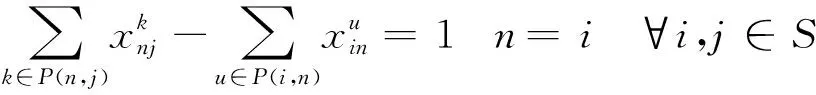
(15)
(16)
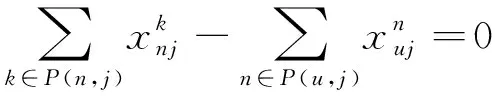
∀n≠in≠jn,j,u∈S
(17)
(18)
式中:M为一个正无穷大数。
式(13)为下层模型的目标函数,旨在实现车流的总相对延误最小化。式(14)表示若不开行i到k的直达列车,那么i到j的车流不能在k站改编。式(15)~式(17)为模型的约束条件,采用流量平衡的思想,确保每支车流被送达至目的地。式(18)表明决策变量为0-1变量。
3 求解模型的模拟退火算法
结合本文模型在求解过程中需要不断循环迭代的特性,选用模拟退火算法(Simulated Annealing,SA)对模型进行求解。
3.1 能量函数
为降低模型求解复杂度,将模型中的复杂约束条件作为惩罚项加入到目标函数中。复杂约束主要是式(9)、式(10),将其作为惩罚项加入到上层规划模型的目标函数中作为能量函数。
H(X)=β1max{0,Fk-θkCRk}+β2max{0,
(19)
式中:β1、β2为正惩罚参数,根据实际经验,分为取值为400、200。
能量函数为
(20)
3.2 初始温度的确定
在确定初始温度时,根据文献[13]先随机产生m个解,则有
(21)
(22)
式中:m+、m-分别为能量函数Z(Xn)值增加、减少的解数;ρ0为给定的初始接受率,一般取0.9~0.99,本文对取值为0.98;Δavg为m+个能量函数增加值的平均值。
3.3 初始解的生成
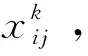
3.4 邻域解的生成
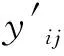
3.5 模拟退火算法步骤
Step1确定初始温度T0。记当前的降温次数k=0,转Step2。
Step2记迭代次数为n=0。初始温度下,按照3.3节中的方法产生初始解并计算能量函数值,转Step3。
Step3当经过k次降温后,在温度Tk下,记第n-1次迭代后的解为Xn-1,为了得到邻域解Xn,随机增加1个或减少1个直达去向,计算出对应的函数值能量Z(Xn),转Step4。
Step4利用Metroplis抽样准则对当前解进行检验,若Z(Xn)-Z(Xn-1)<0,则无条件接受Xn代替Xn-1;若Z(Xn)-Z(Xn-1)>0,则以概率γn(Tk)接受邻域解。γn(Tk)为
(23)
转Step5。

Step6算法收敛终止判定。本文设置了两个终止准则:一种是接受率小于给定的阈值时,另一种是能量函数在多次迭代过程中保持不变,两个准则满足一个即结束该算法。否则,转Step7。
Step7按如下公式进行降温:
(24)
式中:参数δ一般取0.4,α一般取0.95;kd为高低温迭代次数的分界点,一般为70;φ(Tk)为Tk温度下能量函数期望值的标准差。
Tk温度下经过降温后,温度更新,此时记降温次数k=k+1,置迭代步数n=0,返回Step3,在新的温度下进行循环迭代。
4 算例分析
4.1 算例背景
以京沪铁路为背景进行案例研究。该线路的主要支点站有:丰台西、南仓、德州、济南西、兖州、徐州北、蚌埠东、南京东、南翔等,分别对其编号为Y1~Y9。其中,德州、兖州、蚌埠东为一般技术站,丰台西、南仓、济南西、徐州北、南京东、南翔为路网性编组站,具体网络结构见图2。
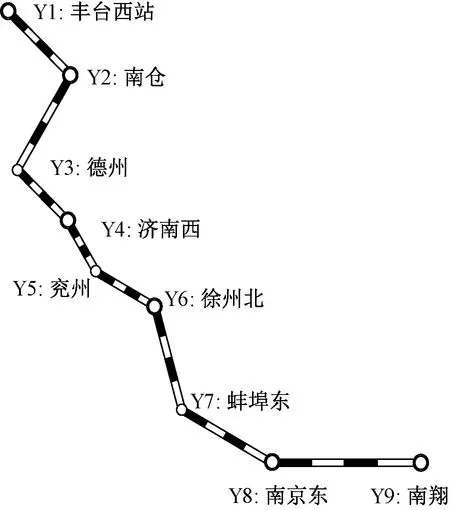
图2 京沪线结构图
4.2 潜在的列车编组去向及无调作业车站
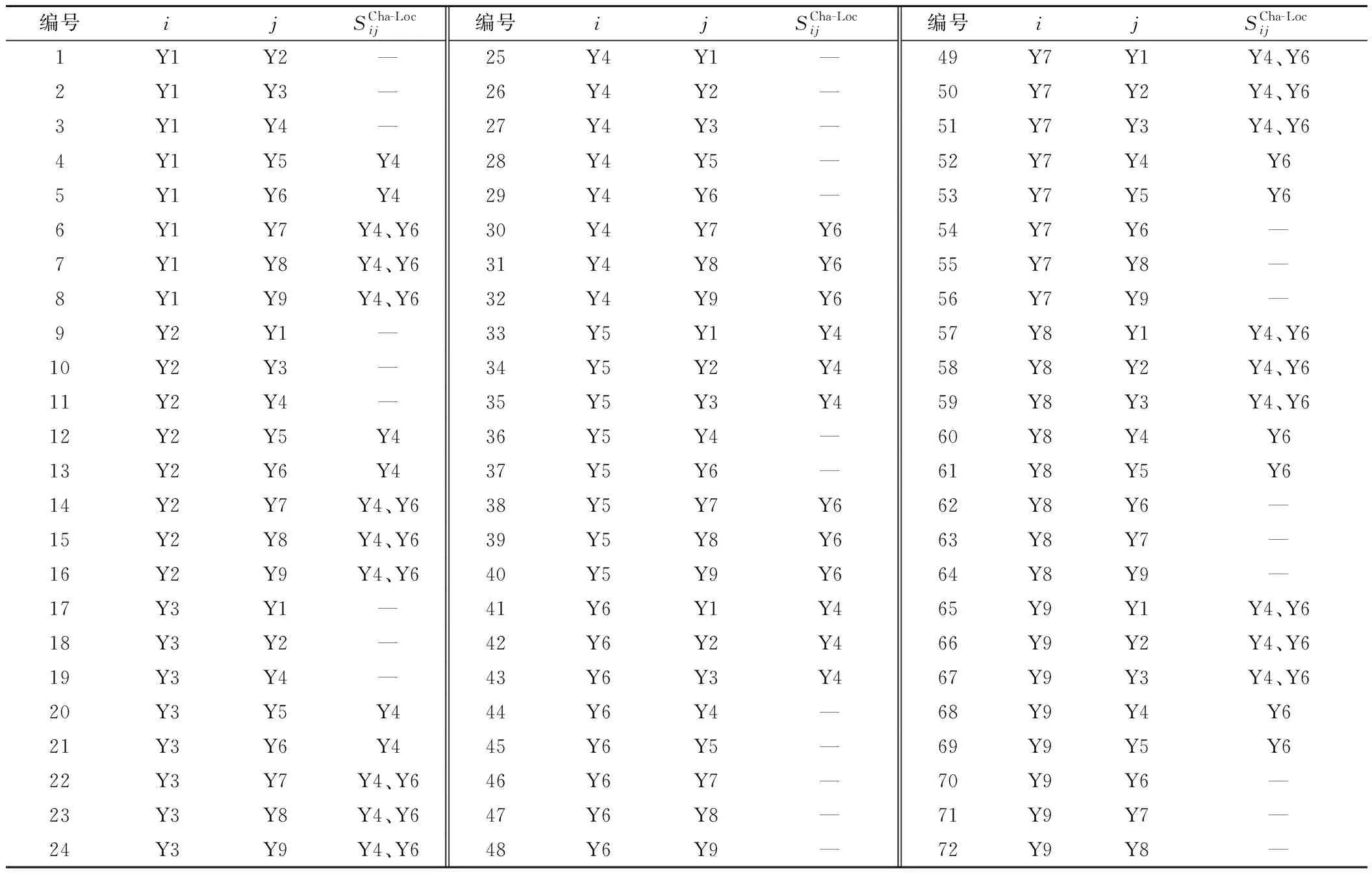
表2 各编组去向换挂机车车站集合
4.3 技术站参数及OD矩阵
目前京沪线各区段的牵引定数普遍在5 000 t,考虑到区段列车编成辆数一般小于远程直达列车的编成辆数,为了不失一般性,本文选取相邻技术站间的区段(直通)列车编成辆数为50车,不相邻技术站间的列车编成辆数为63车。9个支点站间的OD矩阵见表3。
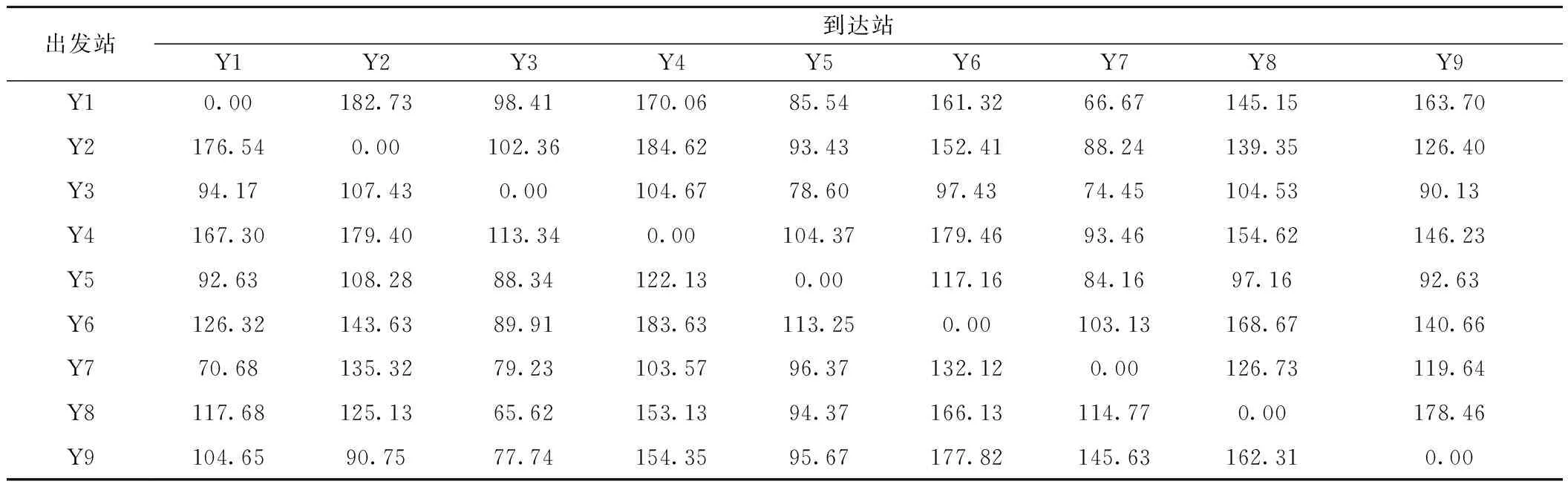
表3 车流OD 车
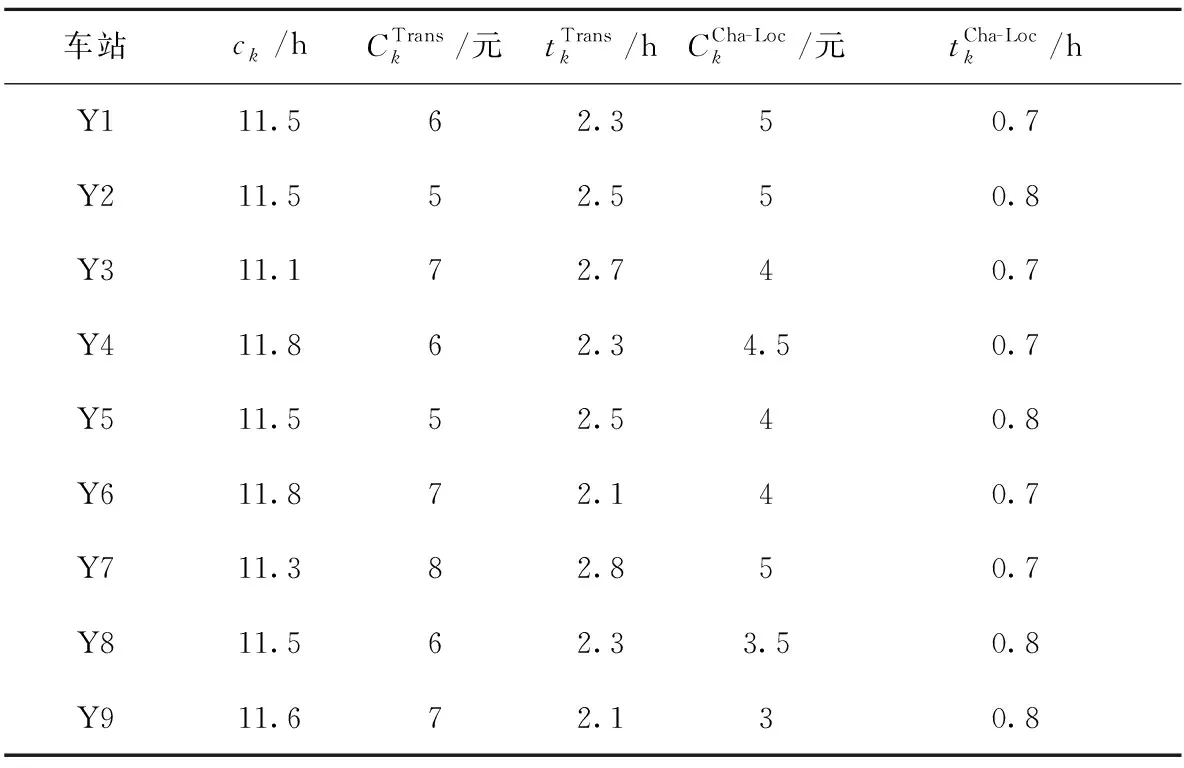
表4 支点站技术参数
各支点站的能力参数见表5。考虑本文的研究算例仅是整个铁路网中的一条通道,未考虑跨线流量,故这里的能力参数是经过理论分析后的剩余能力。例如,以丰台西编组站为例,它是一个双向系统的路网性编组站,其上下行系统的合计解体能力达万车以上,两个调车场的股道数量达百条之多,如果在该算例中仍采用其实际的能力参数,那么相当于在一定程度上松弛掉了某些约束。因此,本文在对能力参数取值时进行了人工处理。比如,在对可用调车线数CTk取值时适当缩小了相应的数值,如果仍采用实际中的CTk,那么相当于在一定程度上松弛掉了上层规划模型中的约束式(10),因此,为了体现其约束性,对技术参数CTk进行了适当的缩减。同理,对CRk也进行了适当地缩减。

表5 支点站能力参数
4.4 结果分析
为了体现本文所建模型的创新性和有效性,基于该算例分别使用文献[5]中的传统模型和本文构建的新模型进行计算,两个模型的不同之处在于文献[5]是传统的货物列车开行方案优化模型,由于默认直达列车在途经技术站时必有无调作业,因而模型中并未考虑无调作业对列车开行方案的影响;而本文的新模型则充分考虑了列车的无调作业产生的影响。
4.4.1 传统模型计算结果
这里需要说明的是,在利用传统模型进行计算时,采用表4中的无改编作业参数,默认列车在途经技术站时必会进行换挂机车等无调作业,并采用式(6)的形式将其无调作业费用作为定值分别计算到对应的直达列车去向yij中(以往认为其为定值,模型中仅有cimijyij而没有将其计算在内),这样做的目的是为了便于与新模型的计算结果进行对比分析,以便突出其优越性。本文同样采用模拟退火算法对传统模型进行求解。最终结果表明,经过46次降温迭代之后完成了优化计算,求解结果确定了12个理论优化编组去向,最终得到上层规划目标函数的最优解为60 965车·h,计算结果见图3。
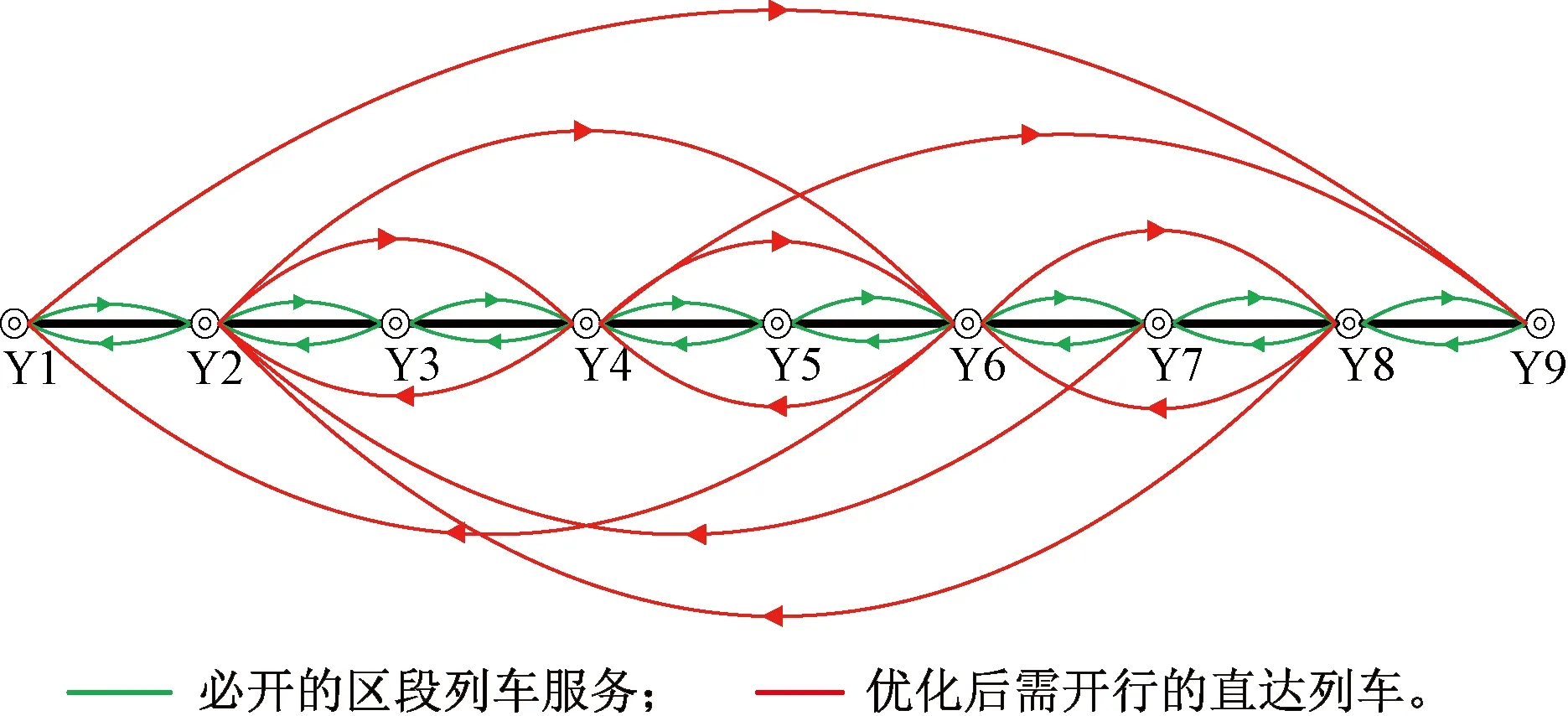
图3 传统模型计算结果
以编组去向Y1→Y8为例进行说明,根据计算结果,Y1→Y8编组去向的车流需要在Y2和Y6进行改编,体现在图中其改编链是(Y1→Y2)∪(Y2→Y6)∪(Y6→Y8)。计算结果中统计见表6,其中中最后一列表示车流改编链,比如(Y1→Y2)∪(Y2→Y3)表示 Y1→Y3去向的车流运输任务由(Y1→Y2)和(Y2→Y3)的列车服务担当。技术站的改编能力和调车线占用情况见表7。

表6 传统模型计算结果统计
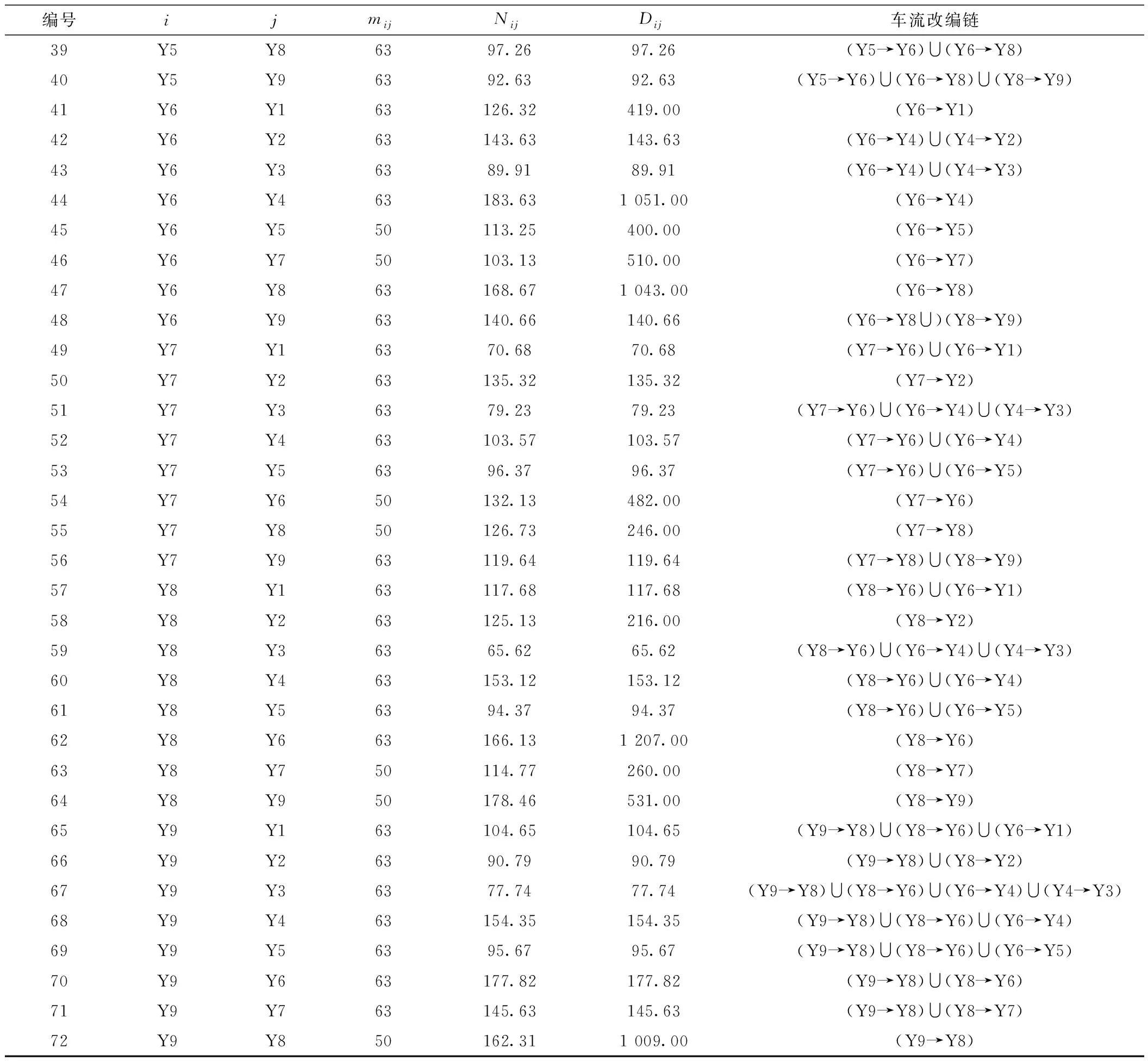
表6(续)
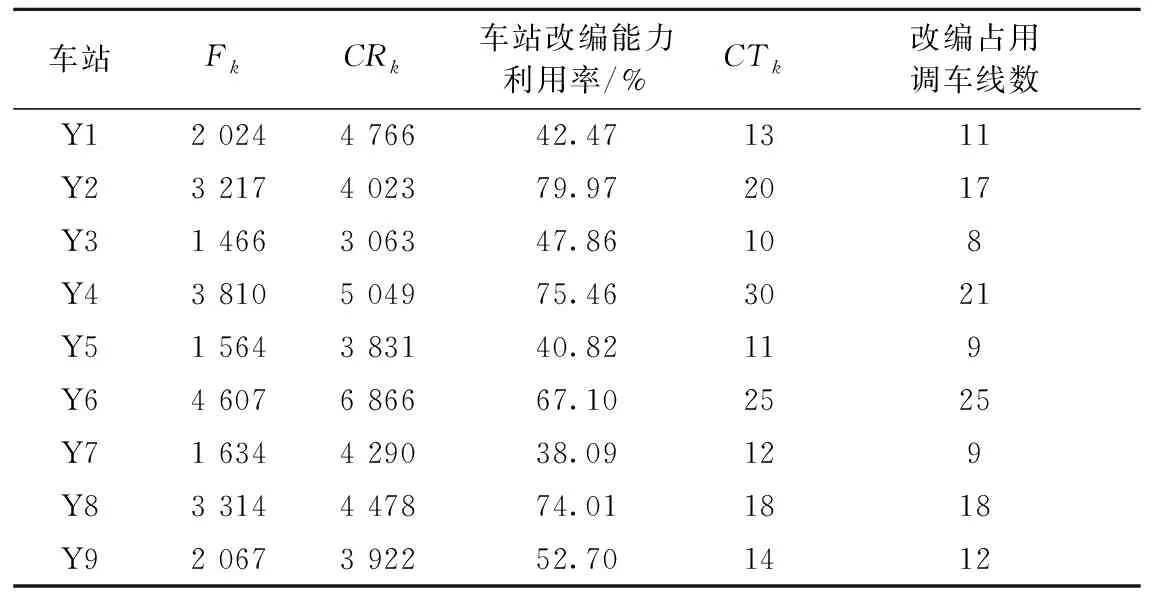
表7 传统模型车站改编负荷及调车线占用情况
4.4.2 新模型计算结果
本文模型的计算结果见图4,根据本文设计的求解步骤,采用VC++程序设计实现,在Core 2.4 GHz的PC机上运行,经过129次降温迭代之后完成了优化计算。求解结果确定了17个理论优化编组去向,最终所得上层规划目标函数的最优值41 390车·h。结果见图4和表8,图中弧段意义和表8中的参数,均与传统模型计算结果中的参数一致。新模型技术站的改编能力和调车线占用情况见表9。
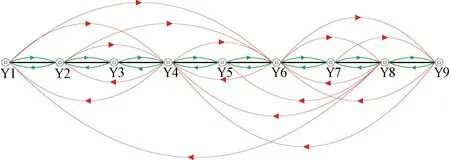
图4 新模型计算结果
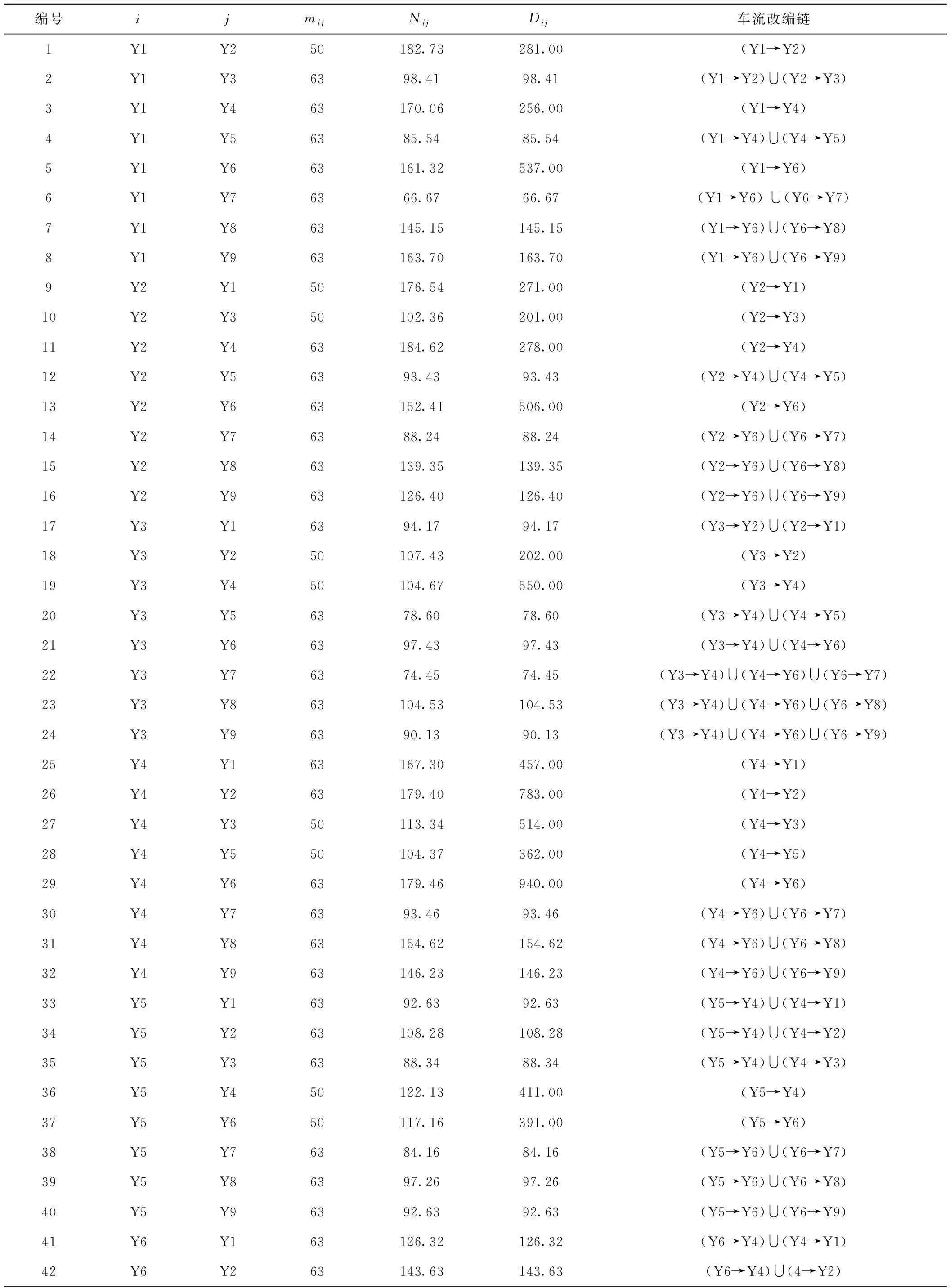
表8 新模型计算结果统计
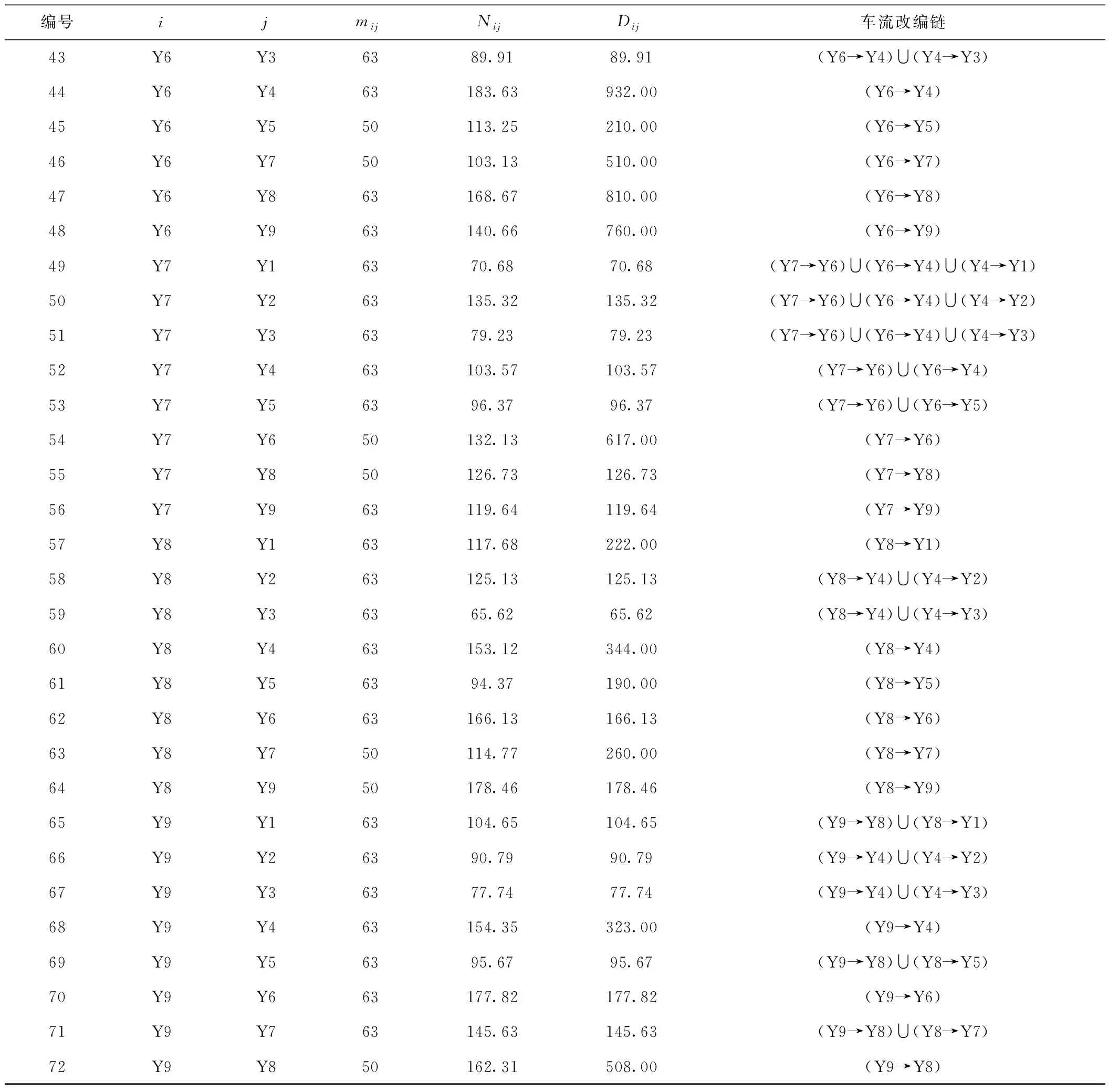
表8(续)
通过对比结果可以看到,本文所建模型的优越性较为明显,传统模型得到的最优开行方案车流开行总成本为60 965车·h,本文所建模型得到的最优开行方案车流开行总成本为41 390车·h,车流开行总成本减少了32%。除此之外,所有车站的总体改编负荷有所下降,由之前的23 703车减少为22 181车。同时,新模型得到的结果也更加符合实际,比如Y7(蚌埠东)到Y2(南仓)的车流,在传统模型的结果中,该编组去向需要开行直达列车。新模型得到的结果中,该编组去向的列车需要在Y6(徐州北)、Y4(济南西)进行改编,这正是考虑了机车交路对列车编组计划的影响。结合实际运行情况,上述两种结果中后者更加符合实际,这是因为蚌埠东是一般技术站,而徐州北和济南西为路网性编组站,在实际车流组织中,蚌埠东的车流一般要先到徐州北进行解体改编,然后进入济南局管辖范围,在到达济南西后进行解体改编,最后进入北京局管辖范围到达目的地。综上分析,新模型得到的结果明显优于传统模型得到的结果,主要体现在车流开行总成本的减少,改编次数的减少和所得结果更加符合实际。
5 结论
本文为适应机车长交路普遍化发展,考虑了机车交路对直达列车无调作业的影响,构建了考虑无调和有调作业的列车开行方案优化双层规划模型。上层规划模型在传统模型的基础上引进了列车的无改编作业费用,旨在实现列车开行总成本最小化。下层规划模型以车流的总相对延误最小化为目标,以流量平衡为约束条件。结合模型求解时需要不断循环迭代的特性,采用模拟退火算法对模型进行求解。所得结果表明,新模型得到的最优开行方案明显优于传统模型得到的开行方案,主要体现在车流开行总成本的减少,所得结果更加符合实际。
