京津冀及其周边地区“2+26”城市PM2.5的蒙特卡罗集合预报试验

曹凯 唐晓 孔磊 王威 吴倩 黄树元 ,4 张佩文 ,4韩丽娜 ,4 吴其重 王自发

1 中国科学院大气物理研究所大气边界层物理与大气化学国家重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 中国环境监测总站，北京 100012

4 成都信息工程大学，成都 610225

5 北京师范大学全球变化与地球系统科学学院，北京 100875

1 引言

京津冀及其周边地区“2+26”城市是当前中国大气污染最严重的地区之一（王恰和郑世林,2019），近年来空气质量虽有所改善，但大气污染整体形势仍十分严峻（程钰等,2019），给社会经济造成巨大损失的同时也对居民健康产生巨大影响（谢杨等,2016）。对空气质量变化进行高精度预报和预测是防控大气污染的关键环节，以多模式集合预报系统为核心的空气质量预报方法已成为我国空气质量业务预报的重要工具之一（王自发等,2009; 王茜等,2010; 陈焕盛等,2013）。

多模式集合预报是基于不同团队研发的模型构建（王自发等,2009; Marécal et al.,2015），通过采用统一的输入数据得到预报集合。在多模式集合预报中，采用合适的集成方法将集合预报系统中不同模式成员集成起来能显著提升空气质量预报效果（Pagowski et al.,2005; 王自发等,2008）。Monteiro et al.（2013）利用多模式集合和中位数法、静态线性回归法、动态线性回归法、贝叶斯模型平均法等集成方法，显著提升了PM10和臭氧的预报效果。黄思等（2015）及潘锦秀等（2019）将多模式集合预报与线性回归集成方法结合起来提升了城市空气质量预报效果。吴剑斌等（2017）评估了多模式空气质量数值预报业务系统对城市臭氧的预报效果，发现采用最优化集成方法的预报效果明显优于单个模式。张天航等（2019）采用了均值集成、权重集成、多元线性回归集成、BP神经网络集成和最优集成等方法提升了多模式PM2.5浓度的预报准确率。谢磊等（2019）基于多个空气质量预测模式，利用最优定权组合法显著提升了SO2预测精度。

多模式集合预报的优点在于考虑各模式物理参数化方案的不确定性，但集合样本数量相对较少，且通常无法充分考虑模式输入场的不确定性，而模式输入场不确定性往往是模式不确定的重要来源（唐晓等,2010）。因此 Hanna et al.（1998）利用蒙特卡罗方法（Mullen and Baumhefner,1994; Du et al.,1997）分析了输入参数不确定性对UAM-IV模型预测结果不确定性的影响。此外，唐晓等（2010）针对模式输入数据不确定性概率分布特征，利用蒙特卡罗方法对模式输入场进行集合扰动，构建了包含50个集合样本的蒙特卡罗集合预报系统，并开展臭氧概率预报的尝试。

相较于单个空气污染数值模式，蒙特卡罗集合预报系统的集合样本数量较多，且能考虑模式输入场的不确定性，为结果提供更为丰富和全面的预报信息。因此本文首先利用蒙特卡罗模拟方法搭建了空气质量的多扰动集合预报系统，并评估此系统对“2+26”城市PM2.5质量浓度的预报效果，然后根据统计参数对集合样本进行筛选，最后利用“集合样本优选”均值集成法对“2+26”城市PM2.5质量浓度进行确定性预报并评估其预报效果。

2 集合预报系统及数据来源简介

2.1 集合预报系统介绍与模拟设置

2.1.1 集合预报系统介绍

嵌套网格空气质量预报模式系统NAQPMS（王自发等,2006）是中国科学院大气物理研究所自主研发的三维欧拉化学传输模式，能模拟大气中污染物的平流、扩散、气相化学、液相化学、干湿沉降等物理化学过程，在大气污染的科研和业务预报上得到了广泛应用。NAQPMS气相化学机制采用 CBM-Z（Carbon Bond Mechanism Z）碳键反应机制，考虑了71种化学物质以及133个核心化学反应；湿沉降和液相化学过程基于RADM中的机制，包含了22种气体和气溶胶；干沉降采用Wesely 方案（Wesely,1989）；气溶胶热力学模块基于 ISORROPIA（Li et al.,2012）。本研究基于NAQPMS搭建了PM2.5的蒙特卡罗集合预报系统。蒙特卡罗集合预报系统框架如图1所示。由于受排放因子、水平活动数据的不确定性以及排放清单更新缓慢的影响，排放清单存在较大不确定性（Cao et al.,2011），因此本次试验仅将排放源中的污染物排放按照其不确定性特征进行随机扰动，产生一组代表排放源不同可能状态的随机集合样本，然后将集合扰动的排放源样本输入至NAQPMS中进行模式积分，最后得到不同输入样本状态下的PM2.5质量浓度集合预报样本。同时考虑到计算资源有限，本次试验仅随机抽取50组扰动样本，从而得到50组扰动状态下PM2.5浓度预报样本。对排放源的扰动方法如下所示：

其中，X0表示扰动前不同物种的排放初值，Xi表示排放物种i扰动后的排放大小，Pi表示排放物种i的扰动系数，其遵循均值为1、标准差为 σ的对数正态分布， σ则通过表1中不同排放物种不确定度大小确定，具体数值来自 Zhang et al.（2009）。

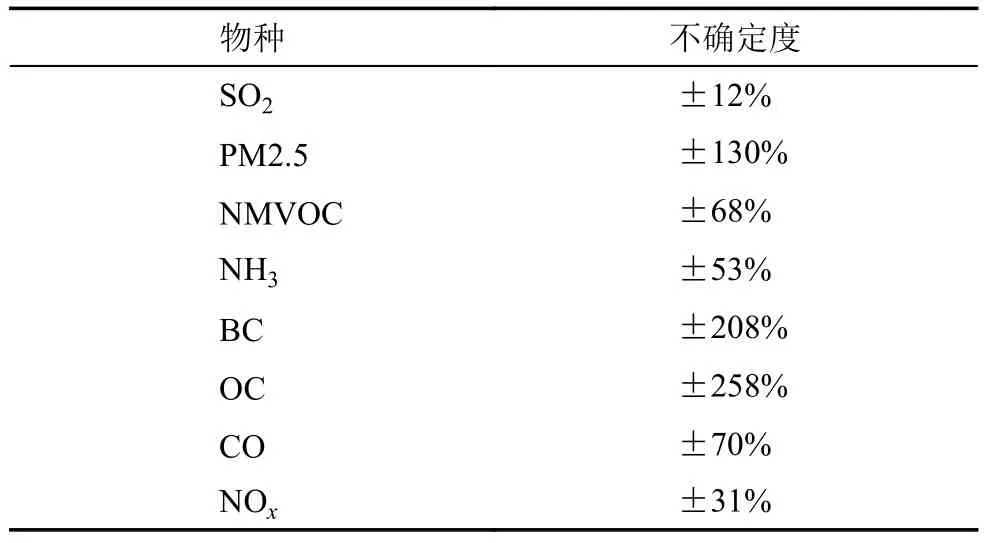
表1 不同排放物种不确定度Table 1 Uncertainties of emissions for different species

2.1.2 气象场模拟设置

本次试验利用中尺度气象模式WRF模拟得出的气象场作为NAQPMS的动力驱动。在设置WRF参数化方案时，分别选用RRTM和Dudhia方案作为长波辐射方案和短波辐射方案，陆面过程选择Noah方案，边界层方案采用YSU方案，微物理方案采用WSM3方案。运行WRF所需的初始和边界条件来自美国国家环境预报中心的FNL再分析数据集，空间分辨率为1°（纬度）×1°（经度），时间分辨率为6 h。另外在每天的气象场模拟中，WRF自由运行36 h，其中前12 h作为模式启动时间，后24 h为NAQPMS提供气象场数据。

2.1.3 NAQPMS 模拟设置

NAQPMS模拟区域及“2+26”城市地理位置如图2所示。采用一层嵌套，以（34°N，105°E）为中心覆盖东亚大部分地区，网格分辨率为15 km，网格个数为432（经向） ×339（纬向）。垂直方向上采用α−z地形追踪坐标系，不等距分为20层，其中2 km以下设置9层，模式层顶海拔高度为20 km。由全球大气化学模式MOZART提供初始场和边界条件。排放源数据中，人为源选用HTAP_v2清单（Janssens-Maenhout et al.,2015）、生物质燃烧源来自 GFED_v4 清单（Randerson et al.,2017）、生 物 源 来 自 MEGAN-MACC（ Sindelarova et al.,2014）、海洋 VOCs来自 POET（http://www.aero.jussieu.fr/projet/ACCENT/POET.php[2019-06-11]）、土壤及闪电 NOx数据分别采用 Yan et al.（2005）和 Price et al.（1997）。试验时段为 2017 年 9～12月，在对污染物进行逐日循环模拟时，集合预报系统都会在初时时刻生成一组排放源的扰动集合，随后将排放源的扰动集合输入至NAQPMS中进行积分，从而得到PM2.5的预报集合。

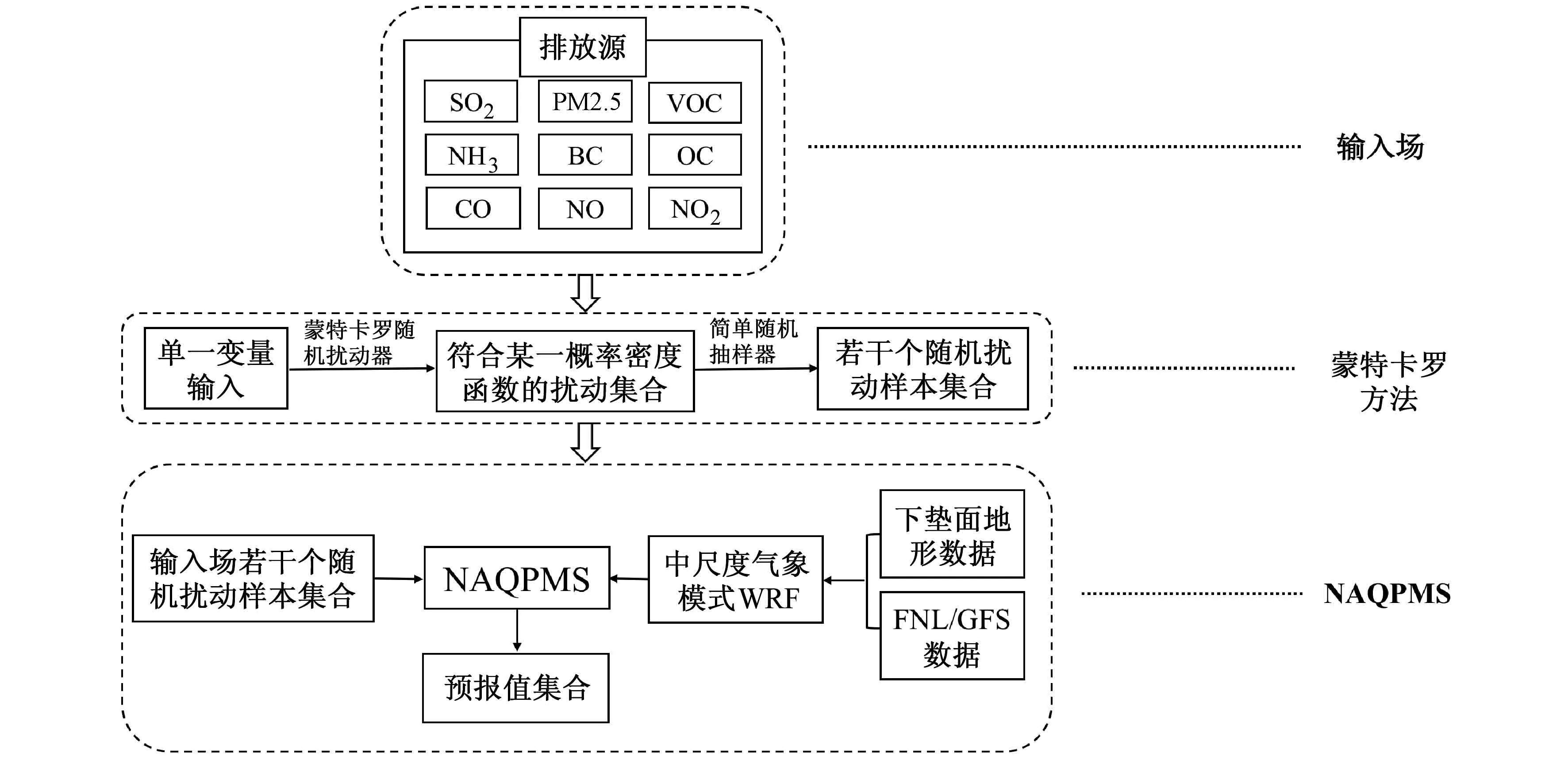
图1 蒙特卡罗集合预报系统框架Fig.1 Framework of the Monte Carlo ensemble forecast system

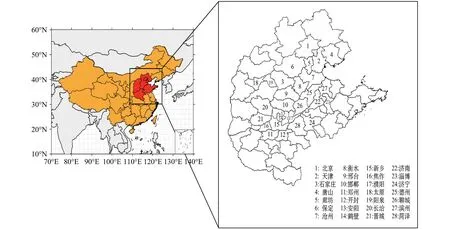
图2 模拟区域范围及“2+26”城市地理位置Fig.2 Simulated domain and locations of "2+26" cities

2.2 数据来源简介

PM2.5质量浓度观测数据来自中国环境监测总站，其中包括“2+26”城市共计161个监测站点2017年9～12月逐时观测浓度，并以该市PM2.5浓度观测值的站点平均代表该市PM2.5质量浓度观测值；PM2.5质量浓度预报值数据来自蒙特卡罗集合预报系统50个集合样本的预报结果。为方便与观测值比较，根据161个监测站点的地理位置，从集合系统预报结果中提取对应网格的PM2.5质量浓度预报值，同样以该市PM2.5质量浓度预报值的站点平均代表该市PM2.5质量浓度预报值。

3 统计集成方法及评估指标简介

3.1 统计集成方法简介

3.1.1 均值集成法

均值集成法是一种简单且常用的集成方法，其预报值可表示为各集合样本预报值的算数平均，公式如下：

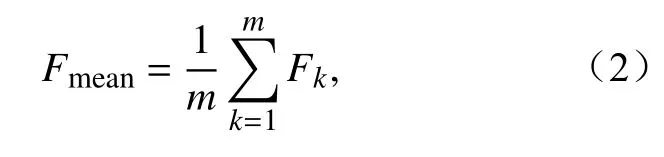
其中，Fmean、m、Fk分别表示均值集成法的预报值、集合样本个数以及第k个集合样本的预报值。

3.1.2 “集合样本优选”均值集成法

Boylan and Russell（2006）曾指出平均分数偏差（Mean Fractional Bias，MFB）和平均分数误差（Mean Fractional Error，MFE）可作为模式对颗粒物质量浓度模拟准确性的衡量指标，具体计算公式如下：

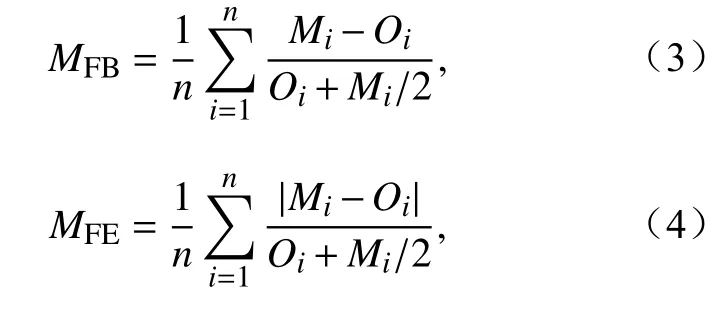
其中，MFB和MFE分别表示MFB和MFE，Mi、Oi、n分别表示第i个时刻模拟值、第i个时刻观测值、有效样本对数，并认为最优模式能够达到的准确性标准为−30%≤MFB≤30%、MFE≤50%。当存在多个集合样本时，利用MFB和MFE可剔除不确定性较大的样本以提高集合样本的整体可靠性。在此基础上，对优选出的集合样本采用均值集成法作为集合预报系统的确定性预报结果。为方便描述，对集合样本优选后采用均值集成的统计方法称为“集合样本优选”均值集成法。

3.2 评估指标简介

均方根误差（RMSE）和相关系数（r）分别表示预报值与观测值之间平均偏离程度和变化趋势相似程度的统计量，具体计算公式如下：

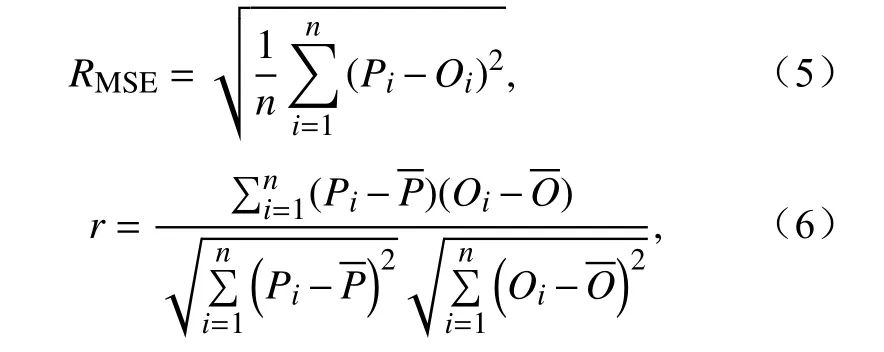
其中，RMSE表示RMSE，Pi、Oi、n、、分别表示第i时刻的预报值、第i时刻的观测值、有效样本对数、预报均值以及观测均值。

4 试验结果

4.1 集合均值预报

为评估蒙特卡罗集合预报系统的预报能力和特点，结合观测资料首先分析各集合样本的PM2.5预报时间序列特征，然后利用RMSE和r等统计参数定量评估均值集成法的预报效果。

图3是保定、沧州、邢台、邯郸、郑州、太原、阳泉、德州等城市利用蒙特卡罗集合预报系统得出的各集合样本PM2.5质量浓度预报值与观测值时间序列对比。由于蒙特卡罗集合预报系统是对排放源进行扰动，并将扰动后的结果入至同一模式中，因此各集合样本间PM2.5质量浓度变化趋势比较一致。此外，各集合样本所构成的预报值集合虽在绝大部分时间段能包含观测值，但大部分样本存在较大的先验模拟偏差，这使得均值集成法的预报值偏高，其余城市也有类似现象。

图3 2017年9～12月“2+26”城市中部分城市蒙特卡罗集合预报系统PM2.5质量浓度预报值与观测值时间序列对比：（a）保定；（b）沧州；（c）邢台；（d）邯郸；（e）郑州；（f）太原；（g）阳泉；（h）德州Fig.3 Comparison of time series of PM2.5 concentration observations and forecast values of the Monte Carlo ensemble forecast system from September to December 2017 in some cities of "2+26" cities: (a) Baoding; (b) Cangzhou; (c) Xingtai; (d) Handan; (e) Zhengzhou; (f) Taiyuan; (g)Yangquan; (h) Dezhou

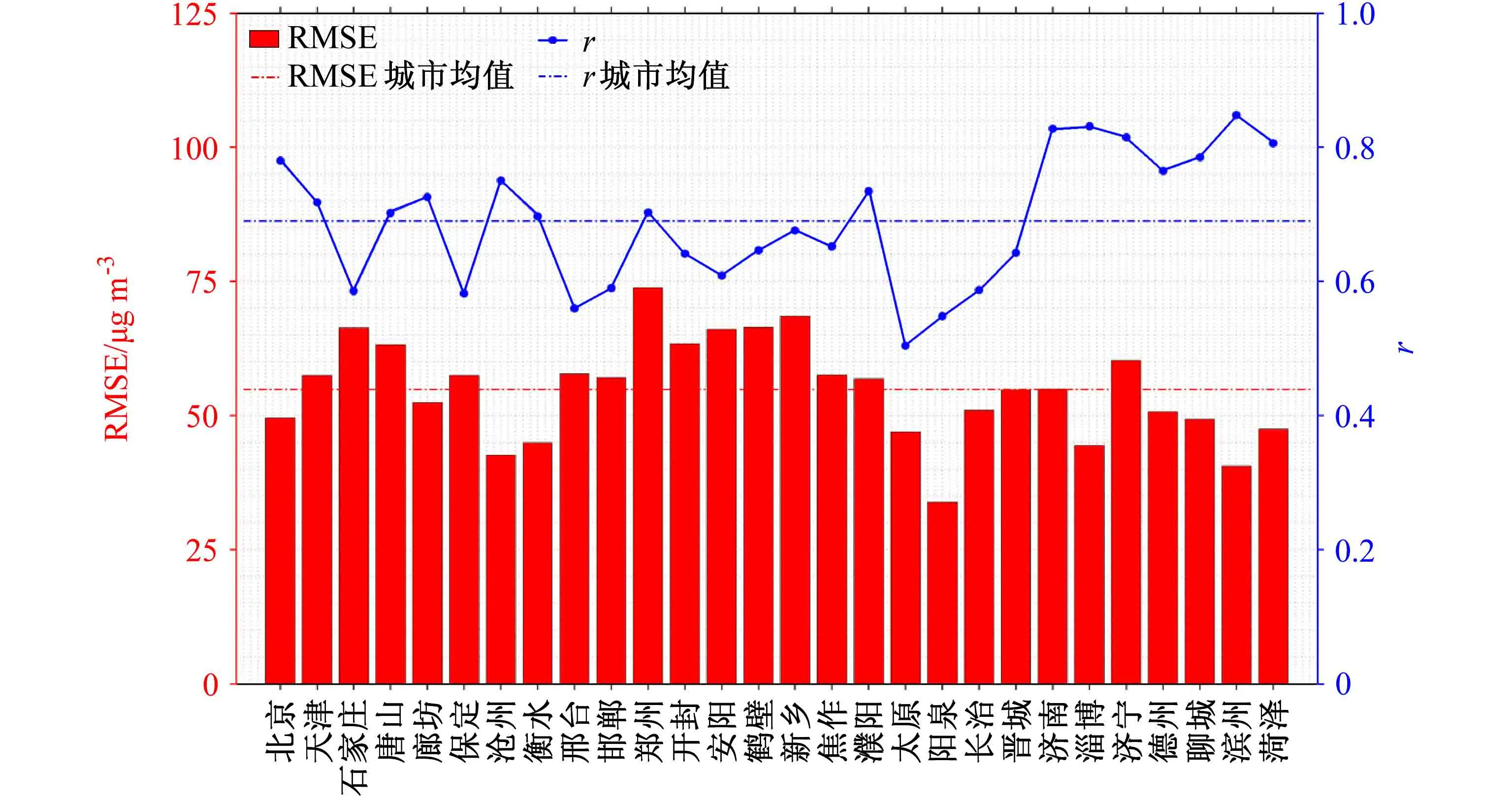
图4 2017年9～12月“2+26”城市均值集成法PM2.5浓度均方根误差（RMSE）、预报值与观测值之间相关系数（r）Fig.4 The RMSE (Root Mean Squared Error) of PM2.5 concentration and correlation between observations and forecast values of PM2.5 concentration with the ensemble mean method in "2+26" cities from September to December 2017

RMSE与r能较好表征出预报值与观测值之间平均偏离程度和变化趋势相似程度，因此利用其定量分析均值集成法对PM2.5质量浓度的预报效果，结果如图4所示。对所有集合样本采用均值集成后，各城市PM2.5浓度预报值与观测值之间相关系数r均大于0.5，r城市均值接近0.7。从平均偏离程度来看，各城市 RMSE 主要集中在 45～65 µgm-3，均值集成法的 RMSE 城市均值接近 55 µgm-3。可以看出，均值集成法虽在PM2.5质量浓度变化趋势上有着较好的把控能力，但由于大部分集合样本存在较明显的先验模拟偏差，使得均值集成法的预报结果高估。

4.2 “集合样本优选”均值预报

考虑到排放清单不确定性对模式结果影响较大（Kong et al.,2019），使得均值集成法预报存在较显著的先验模拟偏差，我们尝试了另外一种方法来集成集合样本。该方法采用滚动预报的方式，首先结合MFB、MFE等统计参数从前30天集合预报样本中优选出符合最优模式准确性标准的样本，然后针对优选出的集合样本，计算其第31天的集合平均值，作为未来1天PM2.5的确定性预报结果。

为了评估两种方法的差异，首先对比分析均值集成法和“集合样本优选”均值集成法的总体预报效果，预报时段均为2017年10～12月，再分析其对各污染等级的预报能力。图5给出了北京、天津、唐山、郑州、鹤壁、新乡、济南、济宁等城市采用两种统计集成方法后的PM2.5质量浓度预报值与观测值的时间序列对比。可以看出，与所有集合样本均值预报相比，“集合样本优选”均值集成法能有效降低预报偏差，使得预报值更加贴近实际观测值。

为进一步分析两种方法的预报技巧，利用RMSE、r和观测—模拟两倍因子百分比（FAC2）等统计参数来评估两种集成统计方法的预报效果。由图6a可见，采用“集合样本优选”均值集成法后，各城市PM2.5预报的RMSE均显著减小，RMSE 城市均值由 58.0 µg m−3降低至 34.7 µg m−3，r城市均值由0.69提升至0.70。FAC2表示预报值落于0.5～2倍观测值范围内的比例（Chang and Hanna,2004），若FAC2越大则表明预报精度越高。从图6b、6c看出，均值集成法的FAC2为67%，有相当一部分预报值大于2倍观测值，高估较为严重。而采用“集合样本优选”均值集成法后，高估现象明显改善，将PM2.5预报的FAC2指标提升至87%。

相对作用特征（ROC）是基于双态分类联列表对双态事件进行检验。对于一次事件的发生与否，预报可分为预报正确、漏报、空报和正确否定四种情况。命中率（hit rate）=预报正确数/（预报正确数+漏报数），假警报率（false alarm rate）=空报数/（空报数+正确否定数）。以假警报率为横坐标，命中率为纵坐标即可构成ROC散点图。若散点落在随机猜测线（即对角线）上或右侧，则表明不具备任何预报技巧；若落在随机猜测线左侧且离随机猜测线垂直距离越远，则表明对该事件预报技巧越高。

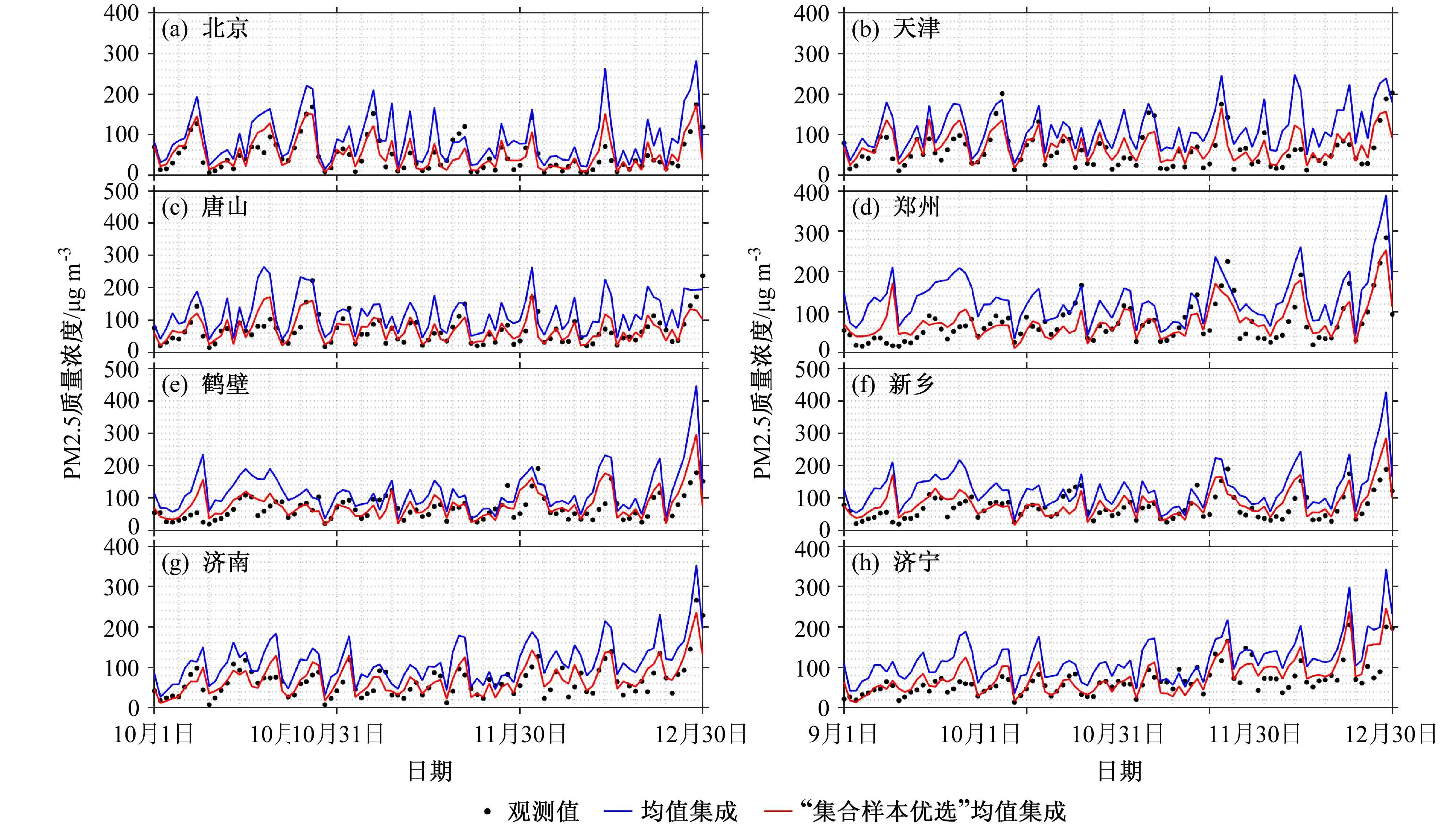
图5 2017年10～12月“2+26”城市中部分城市不同集成统计方法预报值与观测值时间序列对比：（a）北京；（b）天津；（c）唐山；（d）郑州；（e）鹤壁；（f）新乡；（g）济南；（h）济宁Fig.5 Comparison of time series of forecast values and observations by different ensemble statistical methods from October to December 2017 in some cities of "2+26" cities: (a) Beijing; (b) Tianjin; (c) Tangshan; (d) Zhengzhou; (e) Hebi; (f) Xinxiang; (g) Jinan; (h) Jining

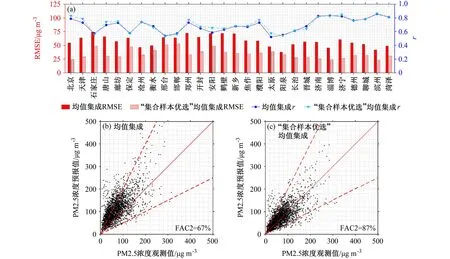
图6 2017年10～12月“2+26”城市不同集成方法的（a）PM2.5浓度均方根误差（RMSE）、PM2.5浓度预报值与观测值之间相关系数（r）；2017年10～12月“2+26”城市（b）均值集成法、（c）“集体样板优选”均值集成法PM2.5浓度预报值与观测值对比Fig.6 (a) RMSE of PM2.5 concentration of different ensemble methods from October to December 2017 in "2+26" cities.Comparison of observations and forecast values of PM2.5 concentration with (b) the ensemble mean method and (c) "collective sample selection" ensemble mean method from October to December 2017 in "2+26" cities

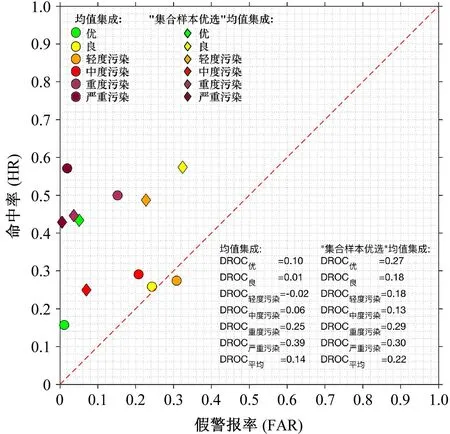
图7 不同集成方法各污染等级的ROC单点分布（DROC表示散点到对角线的垂直距离，负值表示散点位于对角线右侧）Fig.7 Single point distribution of ROC (Receiver Operating Characteristic) for each pollution level with different ensemble methods(DROC is the vertical distance from scatter to the diagonal,and a negative value indicates that the scatter is located to the right of the diagonal)

结合《环境空气质量指数（AQI）技术规定（试行）》（中华人民共和国生态环境部，2016），利用ROC散点图对比分析两种集成统计方法对空气污染等级分别“优”、“良”、“轻度污染”、“中度污染”、“重度污染”、“严重污染”等事件的预报技巧，结果如图7所示。采用所有集合样本的均值集成法时，空气污染等级为“良”、“轻度污染”和“中度污染”的DROC值分别为0.01、－0.02和0.06，说明均值集成法对上述事件的预报技巧非常低。而采用“集合样本优选”均值集成法后，“优”、“良”、“轻度污染”、“中度污染”、“重度污染”等事件的DROC值明显增大，预报技巧显著提升，说明“集合样本优选”均值集成法对各污染等级的整体预报技巧要高于均值集成法。值得注意的是，“集合样本优选”均值集成法对“严重污染”事件的预报技巧略低于均值集成法，这种现象可能与所有集合样本的均值集成法存在较大模拟偏差有关，这种显著高估导致其对“严重污染”事件预报正确的概率较高。

5 结论

本文在嵌套网格空气质量预报模式系统NAQPMS的基础上，结合蒙特卡罗模拟方法搭建多扰动空气质量集合预报系统。从该系统对京津冀及其周边地区“2+26”城市PM2.5质量浓度预报结果可以看出，在所有集合样本均值集成法的预报值存在较大先验模拟偏差的情况下，采用“集合样本优选”均值集成法能显著改善各城市PM2.5预报效果，减小PM2.5预报偏差。

此外，多扰动空气质量集合预报系统具有一定局限性，PM2.5预报效果存在较大提升空间。首先，本次试验主要考虑排放源的不确定性，对模式自身物理、化学过程不确定性以及气象场不确定性考虑较少，根据 Li et al.（2019）研究表明，气象场不确定性对京津冀地区重霾期间的PM2.5模拟效果产生较大影响，因此未来可在多模式集合预报系统基础上，结合蒙特卡罗模拟方法对排放源和气象场进行扰动，构建多模式多扰动的超级集合预报系统，从而更好考虑输入场和模型动力框架不确定性对PM2.5预报效果的影响；其次，对集合样本采用合适方法进行集成之前可利用偏差订正等技术降低集合系统所存在的先验模拟偏差；最后，本研究仅针对符合最优模式准确性标准的集合样本采用均值集成法来提升PM2.5质量浓度预报效果，即赋予每个优选集合成员相同的权重系数，未来可考虑进一步利用多元线性回归、神经网络模型等方法对优选出的集合样本进行集成以此来提升PM2.5预报精度。