两矩形高层建筑的风致干扰效应
2021-04-02刘慕广何勇谢壮宁
刘慕广,何勇,谢壮宁
(华南理工大学亚热带建筑科学国家重点实验室,广东广州 510641)
高层建筑群间存在复杂的干扰效应[1],产生风致干扰的因素众多,建筑的横断面形状是其中一个关键的影响因素.作为高层建筑中最为常见的方形和矩形断面,当前研究工作多以此类截面为对象开展.谢壮宁、顾明等[2-5]对方形高层建筑间的干扰效应进行了系统性的研究,分别探讨了2栋、3栋高层建筑间复杂的干扰效应,指出相较于2栋建筑,3栋建筑间的干扰效应在某些工况下约有80%的增幅.马文勇等[6]采用测压风洞试验,分析了两方形断面高层建筑间的风致干扰机理,认为建筑间平均、脉动的干扰机理可归结为窄道加速效应、遮挡效应及尾流涡旋叠加增强效应,并认为提高湍流度会减弱干扰效应.Kim等[7]通过测压风洞试验,研究了不同高度比下施扰、受扰方形建筑间的干扰效应,认为高度比分别为1.0和1.5时,相近施扰建筑会对受扰建筑的基底弯矩产生极为显著的增大作用.Lo等[8]结合刚性气弹模型和高频天平测力风洞试验,分析了施扰建筑分别处于上、下游时两方形建筑间的干扰效应,认为处于下游的施扰建筑同样会对结构的风荷载产生放大效应.Hui等[9]通过测压风洞试验,研究了方形和矩形(长宽比为3)两类常见高层建筑扭矩间的干扰效应,结果显示干扰导致的平均和脉动扭矩可分别达到单体状态的3倍和1.6倍.Yu等[10-11]基于风洞试验,系统分析了不同宽度比下两栋方形超高层建筑的风致加速度特性,认为宽度比为0.4时,顺风向和横风向加速度的干扰系数可分别达到2.3和3.0,且湍流度对加速度的干扰效应存在抑制作用.Sy等[12]通过风洞试验,研究了方形高层建筑顶部绕流对受扰建筑的影响,结果显示顶部绕流会导致受扰建筑迎风面的平均压力系数增幅46%,且在小间距时会使受扰建筑出现小幅的涡激共振响应.
近数十年间,针对方形高层建筑间的干扰效应,很多学者做了大量开创性的研究工作,并在荷载与响应干扰效应方面取得了一些共识,部分研究成果已编入荷载规范中[13].与之相对,矩形高层建筑间的干扰效应报道较少,而工程实际中,矩形或类矩形断面的高层建筑在城市建设中比比皆是.对于矩形断面,尤其是长宽比较大的矩形断面,气流的分离再附及其与尾流中旋涡脱落的相互作用与方形断面是不同的[14-17],并进一步导致相互间的气动干扰效应存在一定差异.基于此,本文以某实际工程为研究背景,采用高频天平测力试验并结合风振响应计算分析了群体建筑间的干扰效应,明确了矩形受扰高层建筑的施扰源是其邻近的、正交布置的另一矩形高层,而非其侧前方的其他高层建筑;在此基础上,分别沿受扰建筑的侧方和后方两正交方向调整施扰、受扰建筑间的距离,分析了风致干扰效应的变化规律.本文研究结果对正交布置的两矩形高层建筑设计与施工具有一定的工程参考价值.
1 建筑概况及其风效应干扰特征
1.1 建筑概况
实际建筑工程由4栋塔楼组成,塔楼分别命名为T1~T4,其中T1为下文要探讨的对象.4栋建筑围成半封闭的U形布局,建筑平面如图1所示.T1塔楼结构标高221.9 m,左半侧出屋面幕墙标高241.9 m,右半侧出屋面幕墙标高232.9 m;建筑139.4 m以下为矩形断面,长、宽分别为62.335 m和31.045 m,长宽比为2.008;建筑139.4 m以上横截面长仍为62.335 m,但左下侧整体突出1.5 m,导致左侧宽度变为32.545 m;以建筑最高点计算的塔楼高宽比为7.79.总体上看,T1塔楼的气动外形仍接近矩形断面.T2塔楼标高197.1 m,横断面为矩形断面,长、宽分别为71 m和25.375 m,长宽比为2.798,高宽比约为7.77.T3和T4塔楼顶部标高均为190 m.
1.2 试验模型与参数
T1塔试验模型采用高强轻质泡沫核心、轻质桐木外形模拟.试验模型缩尺比为1 ∶300,模型底部与高频测力天平连接.整个模型测试系统x轴向的第一阶固有频率为46.5 Hz,y轴向第一阶固有频率为38.5 Hz.
风洞试验在华南理工大学风洞实验室进行,图2为试验模型.试验模拟了工程周边600 m半径内的建筑,在T3、T4北侧150 m范围内有3栋高度在190~350 m的超高层建筑,T2东南500 m处有1栋高度260 m的超高层建筑.试验中采用尖塔和粗糙元模拟出《建筑结构荷载规范》[13]中的C类风场,其平均风速、湍流度剖面模拟结果见图3,图中Vz为300 m高度处的平均风速.

图2 试验模型Fig.2 Test model
试验中高频天平系统的采样频率为400 Hz,样本采样长度为40 960点.试验中以10°为间隔,获取了0°~360°风向下T1塔楼的气动力,试验风向如图1所示,正东向定义为0°方向角.
1.3 风致响应计算方法
假定高层建筑的一阶振型随高度线性变化,按照阵风因子法,线弹性结构考虑动力放大作用的峰值基底弯矩M^可表示为[18],
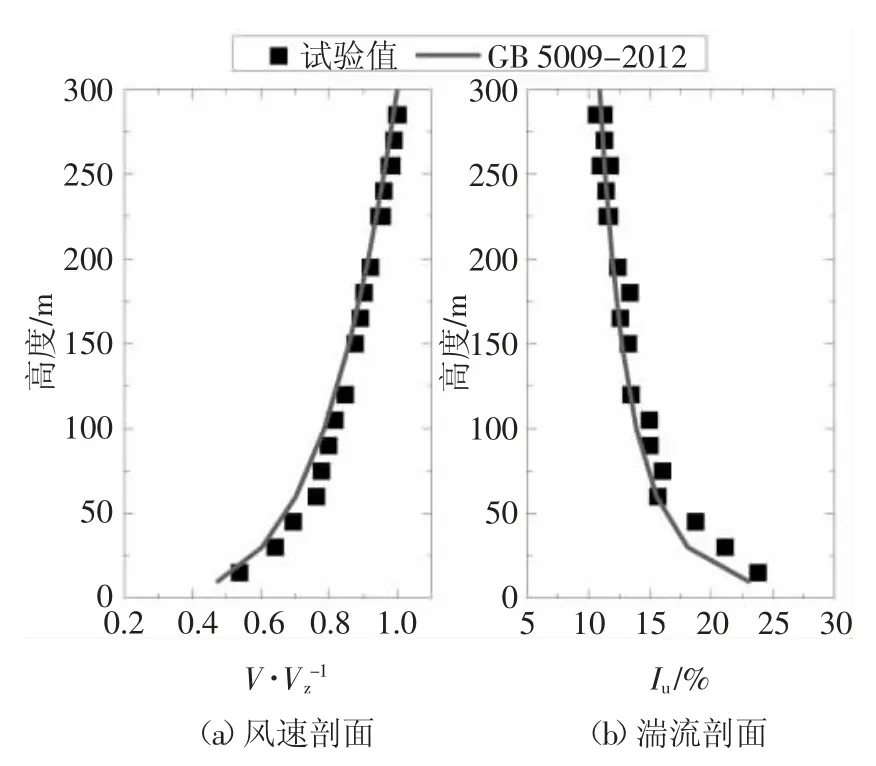
图3 C类风场模拟结果Fig.3 Simulated wind parameters in terrain C
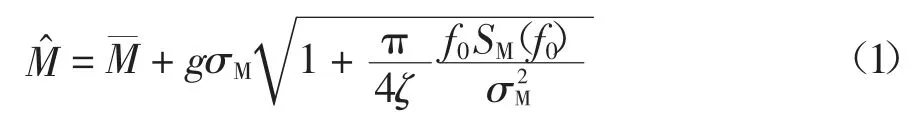
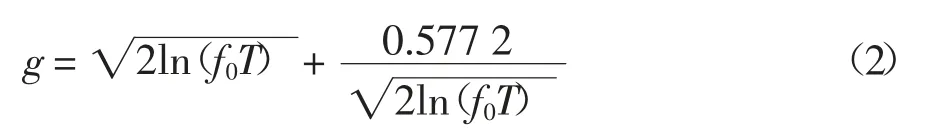
式中:T取600 s.
考虑到加速度响应以共振分量为主,相应的结构顶部的峰值加速度a^可采用式(3)计算[18],
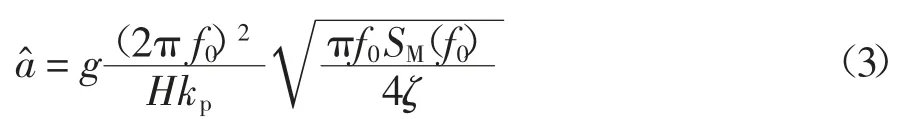
式中:H为结构高度,kp为模态刚度.
1.4 气动干扰特征
对T1塔分别进行了单体和群体状态的风洞试验,风振响应分析中结构x轴向和y轴向的模态频率分别为0.19 Hz和0.158 Hz,计算采用的结构阻尼比为5%.图4为单体和群体状态下T1塔基底弯矩响应的极大值、平均值和极小值随风向角变化情况.
由图4可见:
1)单体状态下,在来流正吹的0°和180°风向角,平均基底弯矩Mx接近0,90°和270°风向角气动力达到最大值;平均基底弯矩My虽然未在正吹的风向角接近0值或最大值,但也在临近正吹的风向角出现.气流作用下矩形断面会产生规律性的漩涡脱落,但从图4中可见,T1结构横风向的峰值基底弯矩并未成为控制荷载,Mx和My最大值分别出现在90°和160°风向角,为顺风向控制.这主要是由于结构频率未落在规律性涡脱频率的峰值附近,致使横风向共振效应并不突出,如图5所示(图中横坐标为模型状态频率,频率比λf=68.1).
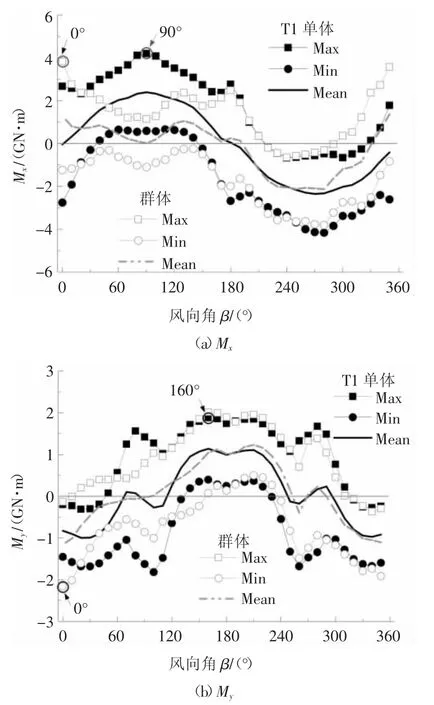
图4 T1风效应随风向角变化Fig.4 T1 wind effects at different wind direction
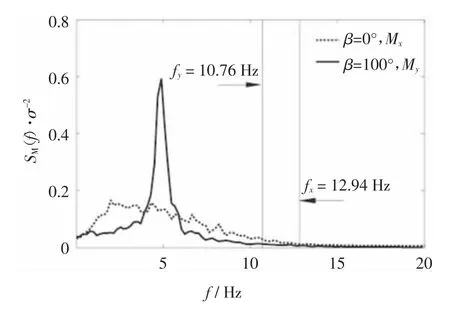
图5 典型风向基底气动弯矩功率谱密度Fig.5 Power spectral density(PSD)of based bending moment at typical wind direction
2)群体状态下,受周边建筑的干扰,T1塔楼基底弯矩Mx与单体状态的差异主要表现在两个风向区间,分别为40°~170°和300°~20°风向区间.其中40°~170°风向产生的干扰效应可以明确主要来自T1上游的几栋超高层建筑,导致其基底弯矩Mx的平均值和峰值减小,并大幅减弱了该区间峰值基底弯矩My的共振响应;在300°~20°风向区间,群体下平均基底弯矩Mx整体在单体的上侧,且随风向角增大相互间的差异逐渐增加,在0°风向角时,群体和单体间的平均基底弯矩差异达到最大,并进一步导致0°风向角下的峰值弯矩明显高于单体状态(约为1.39倍),且成为全风向的设计控制弯矩.同时,0°风向基底弯矩My的平均值也高于单体状态,峰值弯矩约为单体状体的1.49倍,且同样成为全风向的最大弯矩.
对于群体状态T1在0°风向基底弯矩异常增大并成为控制弯矩的原因,由图1和图2可见,其上游并未有其他干扰建筑,最可能的干扰来源有两组,其一为侧后方的T2塔,其二为侧前方的T3和T4塔.为了探明T1塔0°风向气动力增大的主导因素,有针对性的进行了两组验证性试验,分别为群体状态下去掉T2塔和仅保留T2塔的试验,风向角为±30°区间.另外,对于仅保留T2的工况,同时进行了150°~210°风向试验,以分析T2处于T1上游时对T1的干扰效应,图6为计算分析后的结果.
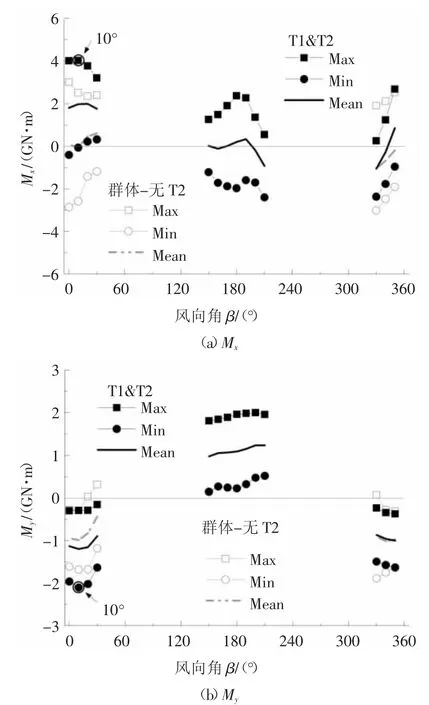
图6 典型风向区间T1塔楼风效应特性Fig.6 T1 wind effects at typical wind direction
由图6可见,去掉T2的群体工况,0°风向下基底平均和峰值弯矩Mx和My均与单体状态接近,峰值弯矩Mx和My分别为单体工况的1.09和1.11倍;而仅保留T2的试验工况,0°风向下的基底弯矩Mx平均值和峰值与上文群体状态类似,峰值弯矩Mx约为单体工况的1.45倍.另外,仅保留T2塔工况下My的平均和峰值也接近群体下的数值,峰值弯矩My约为单体工况的1.35倍.也就是说,上文群体状态中T1塔0°风向气动力增大并成为控制荷载的主要原因为T1侧后方的T2导致,T3和T4虽有影响,但不是主要因素.对于T2处于T1上游的情况,由图6中150°~210°风向结果可见,其Mx和My随风向的变化规律均与群体状态类似,150°~210°风向区间的最大值甚至要略低于群体状态.需要进一步指出的是,仅保留T2的14个试验风向角,0°风向基底弯矩Mx和My已不是最大荷载,其最大值出现在10°风向.以上分析可见,对于本文正交布置的两矩形高层建筑,T2处于T1侧后方较位于侧前方对T1的气动干扰效应更为显著.
《建筑结构荷载规范》[13]对两方形高层建筑在T1、T2这一间距下的顺风向和横风向干扰系数建议值均为1.0~1.1,由上文分析看,本文两矩形高层间0°风向时的顺风向干扰系数为1.49,横风向干扰系数为1.39,均高于规范建议值.考虑到现有矩形高层建筑间气动干扰的研究比较有限,也缺乏相应的工程设计建议,因此,下文中基于T1和T2塔楼的建筑布置,适当进行了拓展研究,分析了间距变化下正交布置两矩形高层的干扰效应.
2 间距变化影响分析
2.1 工况布置与数据处理
考虑到T2处于T1下游的气动干扰更显著,所以基于当前建筑布局,仅研究了T2处于T1后方和侧方不同间距时T1风效应的变化,即T2分别沿-x和+y两个正交方向改变间距比.拓展试验仅针对图1中的0°风向角进行,当T2沿-x移动时,y轴向的形心距y/B=2.13保持不变;当T2沿+y方向移动时,x轴向的形心距x/B=1.51保持不变.
T2对T1风振响应的影响采用干扰因子进行评估,其定义为:

式中,R和Rs分别为干扰状态和单体状体建筑的风效应.一般来说,结构的风致响应与结构的固有频率及所处场地的基本风压有关.为了不失一般性,结构风效应分析中仍采用T1的固有频率,即fx=0.19 Hz和fy=0.158 Hz,但考虑了基本风压w0在0.1~1.1 kN/m2(间隔0.1 kN/m2,基本涵盖了中国大部分地区的基本风压)变化时结构的风效应特性,最后取各基本风压下IF的包络值作为干扰系数的代表值,即:

2.2 干扰规律
基于高频天平得到的平均风荷载及建筑迎风面面积,可得到建筑的等效体型系数,其干扰系数如图7所示.图7中纵坐标为干扰因子,横坐标为T1和T2间的无量纲距离,定义为x或y轴向的两建筑形心距与T1宽度(B=31.045 m)的比值,下文同.试验中T1单体状态的等效体型系数分别为μsx=1.15和μsy=0.03.由于单体状态横风向体型系数接近于0,在进行横风向干扰系数计算时,统一采用单体顺风向的体型系数归一化.
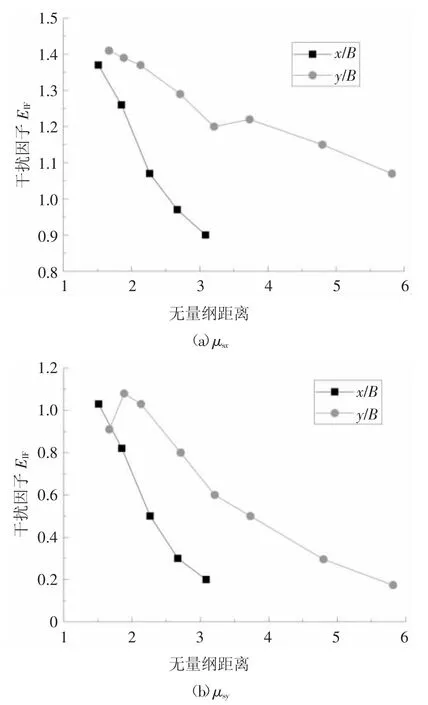
图7 体型系数干扰因子随间距比变化Fig.7 EIFof shape factor varies with space ratio
由图7(a)中顺风向体型系数干扰因子随间距比变化可见,随x/B增大,干扰因子由1.37迅速减小至0.9;随y/B增大,干扰因子整体上也呈现递减的趋势,其最大值为1.41,间距比接近6时为1.07,仍呈放大效应.虽然T2沿T1侧向(y/B)和后方移动(x/B)均会降低对T1的气动干扰,但向后方移动时干扰因子衰减更为迅速,出现这一现象的原因极有可能与T1、T2的正交布局,即T1窄边迎风、T2宽边迎风相关.
由图7(b)中横风向体型系数干扰因子随间距比变化可见,小间距比下的干扰因子甚至会超过1.0,也就是高于T1单体状态顺风向的体型系数,也明显强于两方形高层间横风向平均风荷载的干扰效应[6].即使x/B和y/B分别达到3.08和5.82,其干扰系数仍接近0.2.与顺风向干扰系数随间距比的变化规律类似,T2沿T1后方移动时干扰效应迅速减弱;T2沿T1侧向移动时,其干扰系数先在间距比y/B=1.88时达到最大值1.08,然后逐渐减小,其衰减趋势同样略缓于-x向移动的结果.
图8为峰值基底弯矩Mx和My干扰因子随间距比变化的结果.由图8(a)可见,考虑共振分量影响后,横风向峰值风荷载干扰系数较图8(b)中平均风荷载干扰系数进一步增大.x/B=1.51和y/B=1.88时,干扰因子分别达到最大值2.21和2.28;x/B=3.08和y/B=5.82时,干扰因子仍高于1.0,呈放大效应.与图7(b)体型系数干扰因子随间距比的变化趋势类似,峰值弯矩Mx对应的干扰因子随x/B增大迅速单调减小,随y/B增大先增大而后缓慢减小.
对于顺风向基底弯矩My的干扰效应,由图8(b)中可见,其数值整体小于同间距比横风向的结果,且与图7(a)中体型系数干扰因子的结果基本相当,也就是说,建筑的顺风向响应主要是由背景分量控制,共振分量占比很小.随x/B增大,最大干扰因子出现在x/B=1.51,数值为1.39;x/B=3.08时,干扰因子为0.95.随y/B增大,其干扰因子先少许增加,在间距比y/B=1.88时达到最大值1.49,而后逐渐减小;y/B=5.82时,其干扰因子为1.07.
对于高层建筑,顶部的峰值加速度过大会影响人居的舒适度,也是结构设计一个主要的控制指标.T1和T2两建筑正交布置下峰值加速度的干扰因子如图9所示,采用式(3)计算时结构阻尼比取2%.由图9中可见,随x/B增大,干扰因子先增大而后减小.x/B=2.27时,达到最大值1.15;x/B=3.08时,干扰因子为0.96,此时可不考虑T2对T1的不利影响.随y/B增大,干扰因子呈现出阶梯状增大的现象.y/B<2时,干扰因子小于1,随间距比增大,干扰因子仅略有提高;随间距比增大至2.13,干扰因子小幅增大至1.06,而后在y/B ≤3.21时,干扰因子基本保持恒定;当y/B=3.73时,干扰因子出现较大幅度跳跃,达到最大值1.23,而后随间距比增加逐渐减小;y/B=5.81时,干扰因子为1.12.
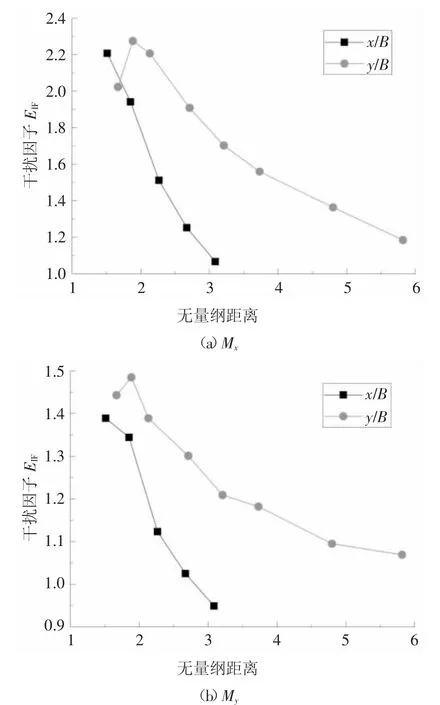
图8 基底弯矩干扰因子随间距比变化Fig.8 EIFof base bending moment varies with space ratio
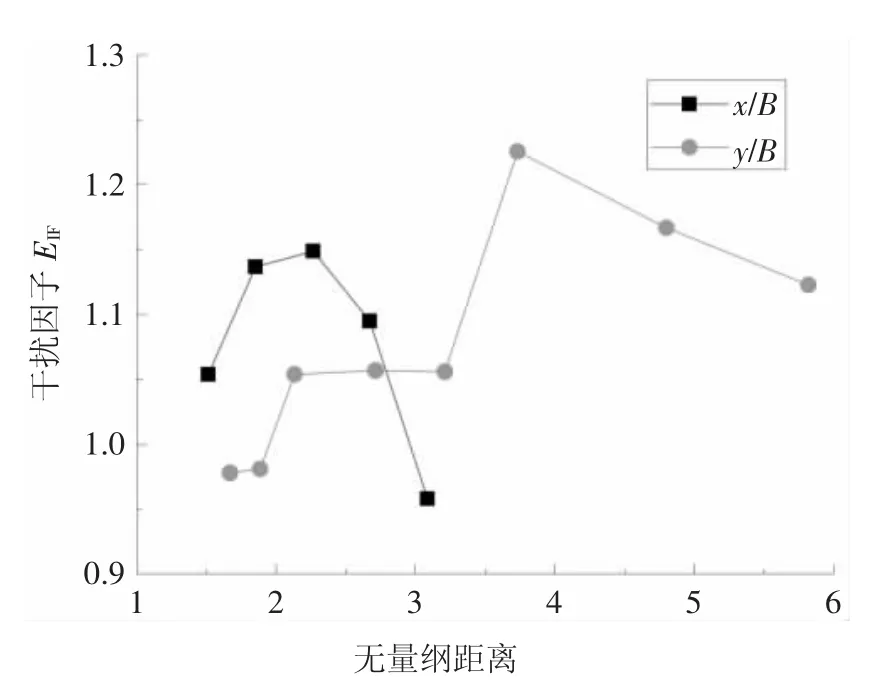
图9 加速度干扰因子随间距比变化Fig.9 EIFof acceleration varies with space ratio
2.3 功率谱分析
图10为典型工况基底弯矩Mx和My的功率谱密度图.由图10可见,施扰建筑对受扰建筑顺风向基底弯矩谱的影响较小,4个典型干扰工况下其能量分布和能量值均与单体状态相近.与之相对,横风向基底弯矩谱则在施扰建筑的影响下,功率谱密度与单体状态存在较为显著的差异.虽然干扰状态能量分布仍呈现“宽带”特征,但干扰工况的能量较单体状态更为集中在低频段,且能量值明显强于单体状态的能量值.这一现象表明,虽然来流湍流风场对建筑的规律性漩涡脱落存在一定的抑制作用,但在施扰建筑影响下,受扰建筑仍出现了较单体时更为规律性的漩涡脱落现象.以上分析可见,施扰建筑的存在对受扰建筑的漩涡脱落形态、涡脱频率及能量构成均产生一定的影响.
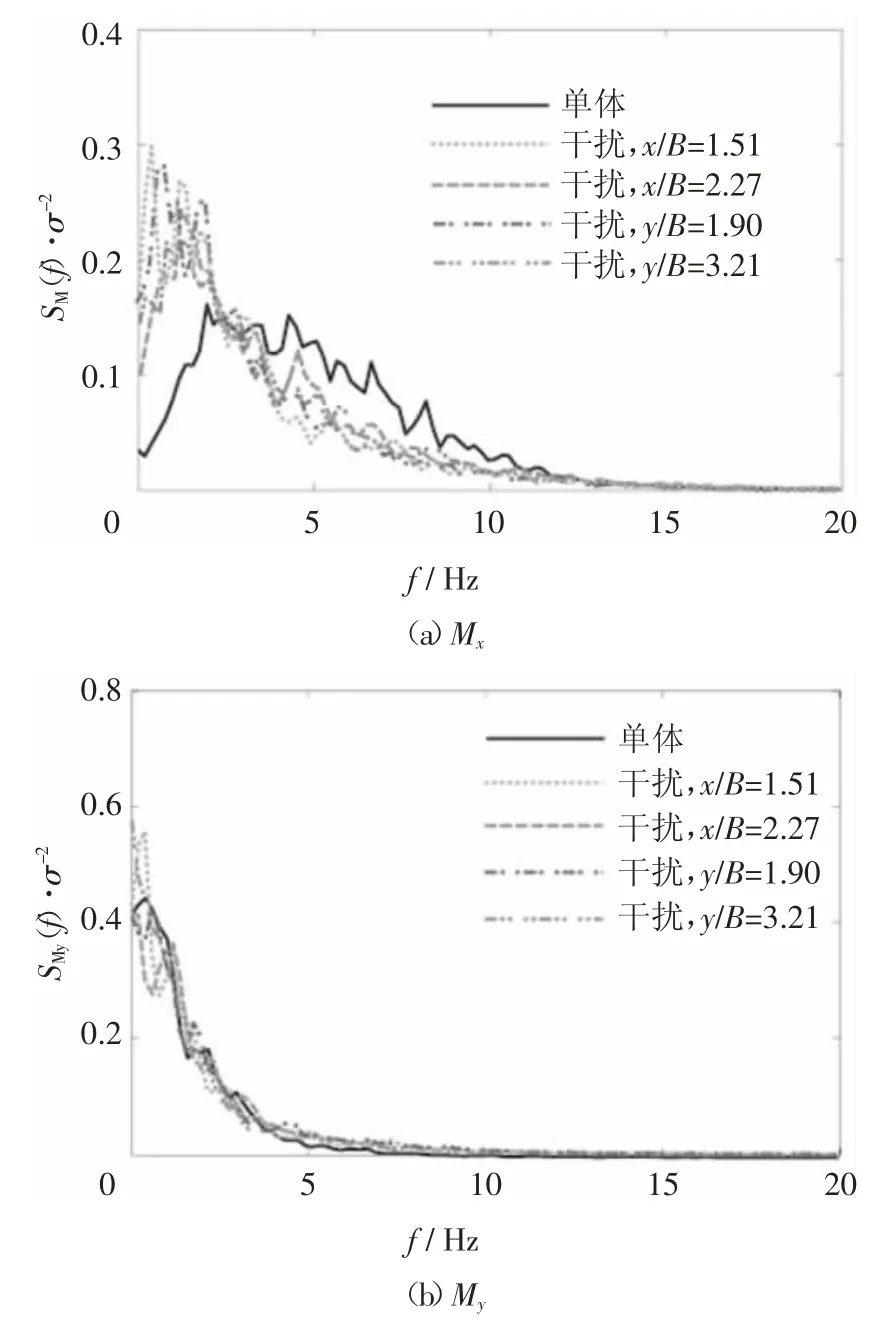
图10 典型工况基底弯矩功率谱密度Fig.10 PSD of based bending moment at typical case
3 结论
1)正交布置的两临近矩形高层建筑应注意相互间的干扰效应,由本文所研究对象看,施扰建筑处于受扰建筑侧后方产生的干扰要强于处于侧前方的情形.
2)风荷载的干扰效应整体上随间距比增大呈递减规律,施扰建筑沿受扰建筑侧方移动时干扰范围和强度明显强于沿受扰建筑后方移动的情形.
3)正交布置的矩形施扰建筑会显著增大受扰建筑的横风向平均风荷载,干扰状态下横风向最大体型系数约为单体状体顺风向体型系数的1.08倍;顺风向体型系数的最大干扰因子为1.41.
4)考虑结构动力放大效应后的顺风向和横风向峰值基底弯矩最大干扰因子分别为1.49和2.28.
5)建筑顶部加速度干扰因子随间距比增加整体上呈先增大后减小的趋势,最大干扰因子为1.23.
本文以实际两矩形高层建筑为研究对象,仅分析了施扰建筑沿-x和+y两方向移动时干扰因子的变化规律,对于评估正交布置矩形高层间的气动干扰稍欠全面,后续将有针对性的开展系统性研究.
