基于郑州地铁下穿南水北调干渠的Peck公式反演分析
2021-04-02田均举肖亚冲郑培信
田均举,朱 坤,蔡 松,肖亚冲,郑培信
(1.河南璟信工程监理有限公司,河南 洛阳 471000;2.河南省交通规划设计研究院股份有限公司,河南 郑州 450046;3.华北水利水电大学地球科学与工程学院,河南 郑州 450046;4.河南省尧栾西高速公路建设有限公司,河南 洛阳 471000)
南水北调工程作为国家重大战略性基础设施,在蓄水运行后,对缓解中国北方水资源严重短缺和南北水资源优化配置上,起到了不可替代的作用[1-2]。然而,随着城市化进程的推进,南水北调干渠与沿线新建工程的空间矛盾愈发明显,与此同时也会产生许多交叉工程。目前出现的交叉工程主要为结构断面小的工程,而且数量较少,如河北磁县污水管道(直径720 mm)穿越通水运行中的干渠[3],石家庄热力管线[4](断面尺寸为4.8 m×3.0 m)、郑州地铁2号线(直径6 m)先于干渠下穿施工[5]等。
关于运用Peck公式预测隧道开挖引起地表沉降的研究成果有很多,如段绍伟等[6]运用修正的Peck公式对长沙地铁隧道施工引起的地表沉降进行了预测研究;郭二新[7]将Peck公式运用于常州地铁隧道施工地表沉降的预测研究中。本文基于上述研究,依据郑州地铁城郊线站场四街站—会展站土压平衡盾构区间穿越南水北调中线干渠的潮河段工程实测数据,将Peck公式法运用于隧道下穿南水北调工程引起的地表沉降预测研究中,并利用反演分析法,通过引入最大沉降量修正系数j和沉降槽宽修正系数k,结合实测数据对Peck公式进行改进[8],得出适用于郑州地区相似工程的Peck公式,以为后期地铁下穿工程引起地表沉降的研究提供经验。
1 工程概况
郑州市南四环至郑州南站城郊铁路工程下穿区间位于站场四街站—会展站区间,隧道设计轴线与南水北调干渠近似直交,交角为91°43′,见图1。左线隧道中心线对应设计桩号为SH(3)156+646.55,右线为SH(3)156+632.55。隧道外径为6 m,内径为5.4 m,管片厚度为0.3 m。

图1 隧道与南水北调干渠空间关系图Fig.1 Spatial relationship between trunk channels and tunnels
隧道下穿处挖深约7.5 m,填高约1.2 m,南水北调干渠的型式为半挖半填渠段。该隧道通过粉质黏土层,地层厚度约为10.2 m,土层中可见少量姜石及小的钙质结核,隧道下穿处地层见图2。
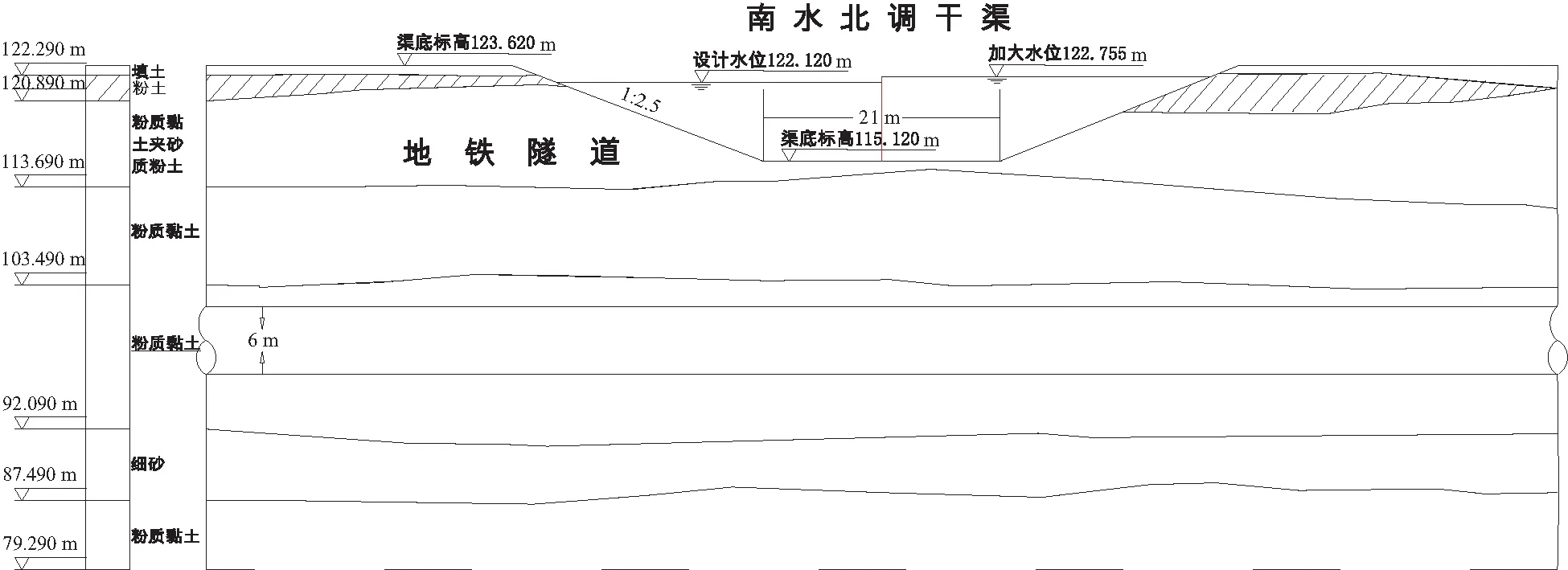
图2 隧道下穿处地层示意图Fig.2 Stratum diagram of the ground underneath the tunnel
2 Peck公式反演分析
Peck[9]根据大量实测数据,提出了隧道开挖引起的地表沉降的地层损失定义,并总结得出Peck公式。在此之后,Peck以及其他学者以Peck公式为基础,对隧道施工引起的地表沉降进行了大量研究,同时也使Peck公式广泛应用于该方面的研究[10]。Peck公式假定:在与隧道轴线平行的方向上,地层损失是均匀的;在与隧道轴线垂直的方向上,其分布情况可由正态分布曲线近似表示[11-14],见图3。

图3 盾构隧道上方地面横向沉降槽Fig.3 Ground lateral settlement tank above shield tunnel
Peck公式可表示如下:
(1)
(2)
式中:x为计算点到沉降曲线中心线的水平距离(m);i为反弯点到沉降曲线中线的水平距离(m),即沉降槽宽度;Vl为地层损失率(%),即单位长度地层损失的体积占单位长度盾构体积的百分比;Smax为地表沉降量的最大值(mm),位于沉降曲线的对称中心;Sx为距隧道轴线水平距离为x处的地表沉降量(mm)。
根据公式(1)和(2),参数i2和x2的关系可表示为
(3)
简化后得出:
(4)

q=g+fp
(5)
将地表沉降数据,运用最小二乘法进行拟合分析[15-16],其回归参数如下:
(6)
(7)
(8)
(9)
(10)
运用上述方法,可得出Smax和i的最佳拟合参数如下:
Smax=eg
(11)
(12)
从而可得到地表沉降量拟合后的回归曲线。
根据统计学方法,利用线性相关系数R来检验回归函数的线性相关关系,有:
(13)
当R>r0.01(n-2)时,则认为回归函数的线性相关性显著。
3 地表沉降数据回归分析
本文以郑州市南四环至郑州南站城郊线盾构隧道下穿区间某一断面为例,按照上述回归分析方法对其地表沉降数据进行回归分析,其回归分析结果见表1。
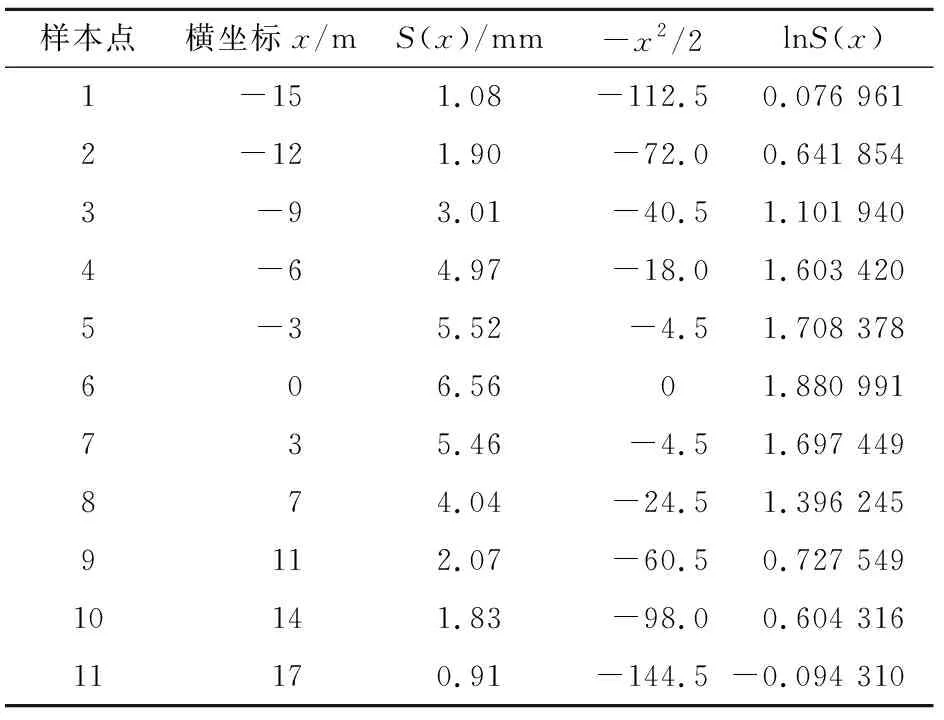
表1 某一断面地表沉降数据回归分析表
将表1中数据代入公式(6)至(12),可计算得出Sxx=24 060.64 mm,Sxy=330.16 mm,Syy=5.69 mm,g=1.754,f=0.014,Smax=5.78 m,i=8.54 m。
将g、f值代入公式(5),可得出回归后的线性函数为
q=1.754+0.014p
(14)
将Sxx、Sxy、Syy代入公式(13),可得出回归函数的线性相关系数R=0.892>r0.01(9)=0.735,认为回归函数的线性相关性显著。
将g、f值代入公式(11)、(12),可得到回归后的Smax、i值,将其代入公式(1)得出拟合后的曲线。实测数据与拟合回归曲线以及Peck公式预测曲线的对比,见图4。
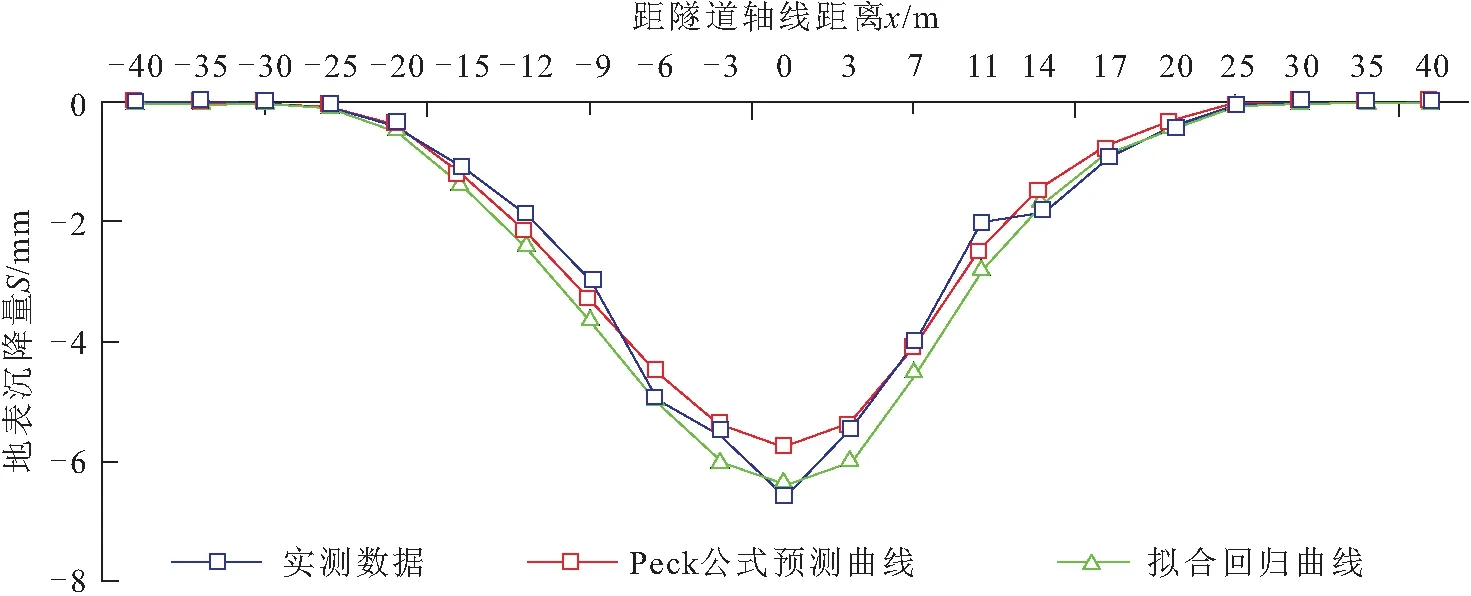
图4 地表沉降量拟合回归曲线分析图Fig.4 Fitted regression curves of surface subsidence data
由图4可见,实测数据曲线与拟合回归曲线吻合度较高,但与Peck公式预测曲线有较大的差异,主要表现在Smax预测方面。其原因可能是由地层条件和工艺法等的差异所产生的[17-18]。因此,需对Peck公式进行改进。
4 Peck公式的改进
针对Peck公式的改进,综合考虑各种影响因素,对沉降槽宽度及最大沉降量进行了修正[19],引入最大沉降量修正系数j和沉降槽宽度修正系数k,改进后的Peck公式如下:
(15)
转化为线性函数如下:
(16)
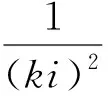
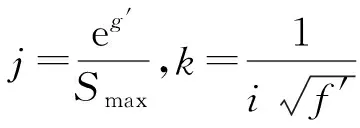
可以得到:j=0.88,k=0.79。
根据上面的方法,选取不同的断面进行分析,得到相对应的修正系数,并对其进行分析。
隧道施工期间,为了保证南水北调干渠的安全以及正常使用,必须加强对地表沉降量的监控测量,监测范围为隧道下穿南水北调干渠对应区间里程前后100 m左右的范围。本文选取29组数据进行分析研究,修正系数的分布情况见表2、表3。

表2 地表最大沉降量修正系数j的分布结果

表3 沉降槽宽度修正系数k的分布结果
对表2和表3中29个断面所得的地表最大沉降量修正系数j和沉降槽宽度修正系数k的分布进行分析可知,当地表最大沉降量修正系数j主要分布于0.7~1.0之间时,其分布比率占到79.31%;当沉降槽宽度修正系数k介于0.5~0.8之间时,其分布比率占到79.31%。由此可以认为,修正系数j、k在上述区间取值时,可以较好地修正由Peck公式预测得到的地表最大沉降量和沉降槽宽度,从而证明了Peck公式法在该隧道下穿南水北调工程引起的地表沉降预测研究中的适用性。
5 不同埋深条件下地表沉降规律分析
郑州市南四环至郑州南站城郊铁路工程站场四街站—会展站土压平衡盾构区间,左线长约2 343 m,右线长约2 466 m,掘进距离长,覆土厚度在7.80~21.80 m之间,埋深多有变化,下穿处隧道顶部距离南水北调干渠底部约12.9 m。由于地层损失率受地层条件和施工方法的影响较大[20-21],且工程所在区域的地质环境稳定、地质条件变化不大、工法一致,因此对于该工程来说,地层损失率变化不大。
假设地层损失率相同对7.8 m(<2D)、12 m(=2D)、12.9 m(3D>H>2D)、18 m(=3D)、21.8 m(>3D)5种不同埋深条件下的地表沉降量进行计算分析[22]。5种不同埋深工况下,隧道施工引起的地表沉降量的理论计算结果见图5。

图5 不同埋深工况下隧道施工引起的地表沉降量的理论计算结果Fig.5 Theoretical calculation values of ground settlement under different buried depths
由图5可见,在其他条件都相同的情况下,随着隧道埋深的增加,地表沉降量曲线逐渐“矮胖”,即地表最大沉降量逐渐减小,沉降槽宽度逐渐增大。
6 结 论
(1) 当引入的地表最大沉降量修正系数j、沉降槽宽度修正系数k分别在区间0.7~1.0和0.5~0.8取值时,可以较好地修正由Peck公式预测的最大沉降量和沉降槽宽度。
(2) 将Peck公式法运用于隧道下穿南水北调干渠引起的地表沉降预测研究中,证明了其在该领域中的适用性。
(3) 通过选取下穿处隧道顶部距南水北调干渠底部分别为7.8 m(<2D)、12m(=2D)、12.9m(3D>H>2D)、18m(=3D)、21.8m(>3D)5种不同埋深工况对地表沉降量进行理论计算,结果表明:在其他条件都相同的情况下,随着隧道埋深的增加,地表最大沉降量逐渐减小,沉降槽宽度逐渐增大。
