直驱容积控制系统响应特性仿真分析
2021-04-01王德文李翠芬
王德文, 衣 超, 李翠芬
(中国北方车辆研究所车辆传动重点实验室,北京100072)
直驱式容积控制系统是新型的泵控电液系统,有着集成度高、闭式无污染、传动效率高等优点[1-2].通过控制电机转速来改变泵的转速,从而驱动液压缸的伸缩运动,最终达到车辆制动的目的.
直驱式容积控制系统是结合电机、机械和液压的复杂耦合系统,电机转矩系数、液压泵死区、液压缸库伦摩擦力和系统泄漏都会对系统产生影响[3-4].系统由电机驱动,存在起步迟滞性[5];液压泵为双向泵,系统死区体积会影响系统响应特性[6];液压缸为差动缸,液压缸的库伦摩擦会产生波动[7];系统为闭式系统,泄漏对其影响较大.
为进一步分析以上因素对系统的影响,搭建了以模糊PID为控制策略的直驱式容积控制系统的AMEsim和Simulink联合仿真模型.
1 直驱式容积控制系统建模
直驱式容积控制系统结构如图1所示,由电机、双向液压泵、液压缸、蓄能器、液压单向阀、溢流阀组成.
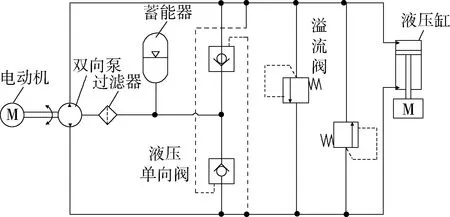
图1 直驱式容积控制系统结构图
电机与液压泵直接连接,工作时电机旋转驱动液压泵,液压泵输出高压油,驱动液压缸运动.液压泵采用双向泵,液压泵的不同旋转方向可实现进油口与出油口的转换.通过电机的正转与反转,带动液压泵正转与反转,实现液压油的不同流动方向,进而实现液压缸的双向供油控制,驱动液压缸的伸出与收回.
1.1 AMEsim仿真模型搭建
直驱式容积系统AMEsim模型搭建根据系统结构图搭建,同时以压力反馈形成闭环.
主要搭建了电机模块(直流电机、温度源、接地、电压输入和转动惯量),液压模块(双向液压泵、蓄能器、过滤器、液压单向阀、溢流阀和液压缸),传感器模块(压力传感器、位移传感器、压强传感器和转速传感器),机械模块(等效弹簧阻尼)以及联合仿真模块.整个系统以电机转速、电流、液压缸压力、液压缸压强、液压缸活塞位移为输入,输入到联合仿真模块,再从联合仿真模块中输出电机电压,进入电机模块形成系统闭环,如图2所示.
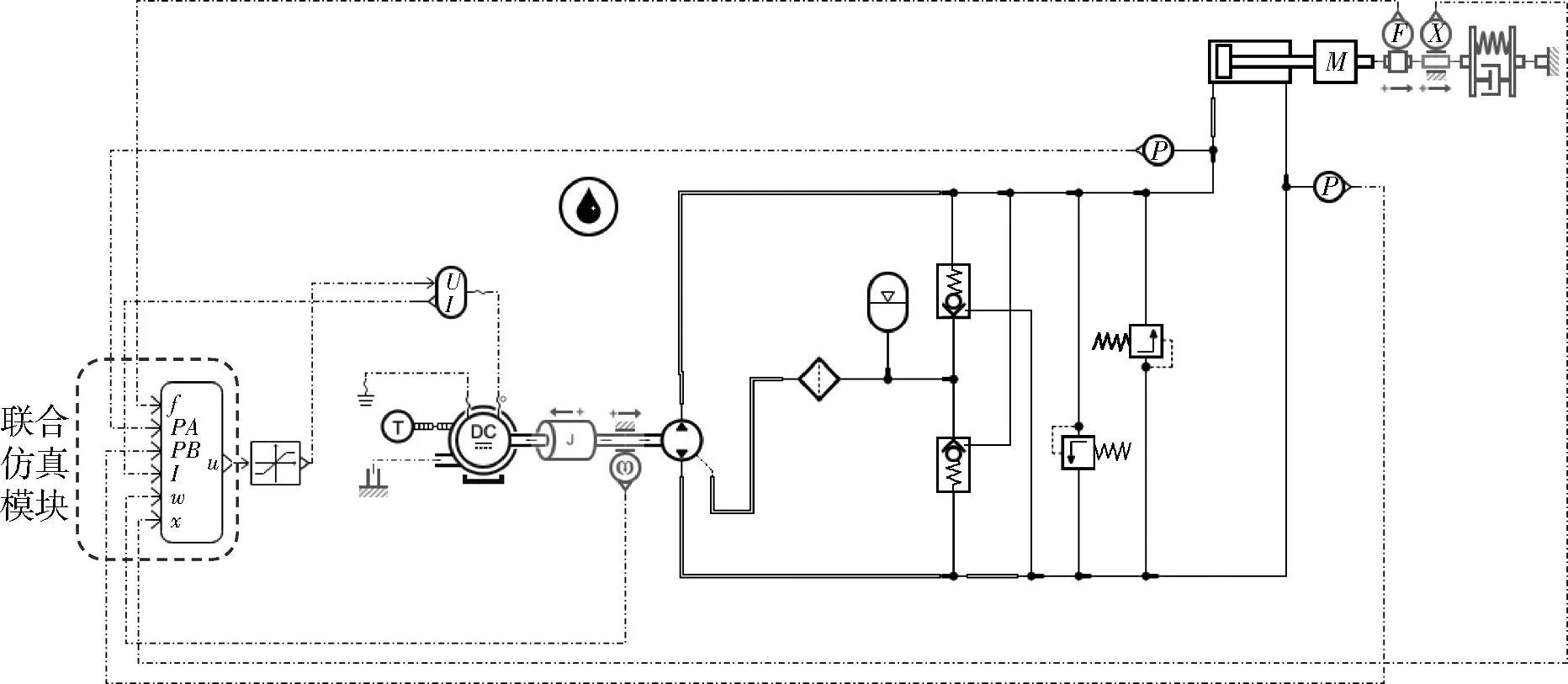
图2 直驱式容积控制系统AMEsim模型图
系统构建的参数如表1所示.
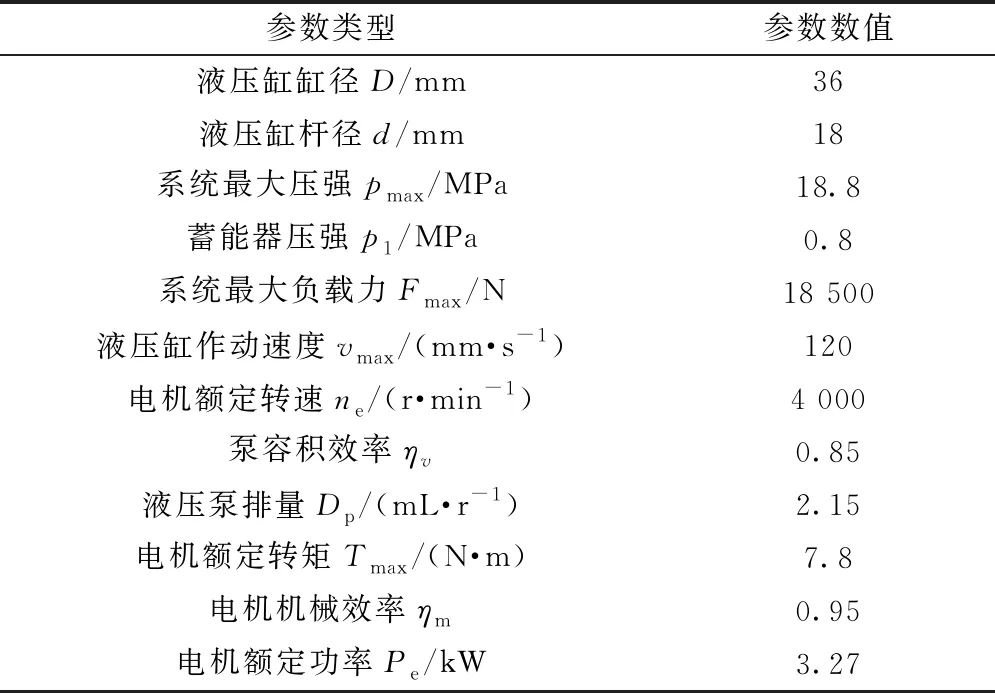
表1 系统构建参数
系统的公式在AMEsim部件的定义中都能找到[8-10],如:液压缸活塞力平衡方程式(1),无杆腔流量方程式(2),电机转矩方程式(3)和液压泵流体体积方程式(4).
F=M·d2y/dt2+bp·dx/dt+k·y+Fl.
(1)
式中:F为活塞压力;bp为系统等效阻尼;k为系统等效刚度;Fl为外负载力.
Q1=V1/σ·dp1/dt+A1·dy/dt+λp1+f.
(2)
式中:Q1为无杆腔流量;V1为无杆腔容积;σ为油液有效体积弹性模量;p1为无杆腔压力;λ为系统泄漏系数;f为液压缸库伦摩擦力.
T=Kt·Ia.
(3)
式中:T为电机转矩;Kt为电机转矩系数;Ia为电机电流.
Va=Vfact+Vd.
(4)
式中:Va为总泵流体体积;Vfact为实际泵流体体积;Vd为泵死区体积.
1.2 Simulink仿真模型
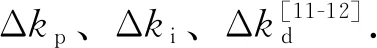
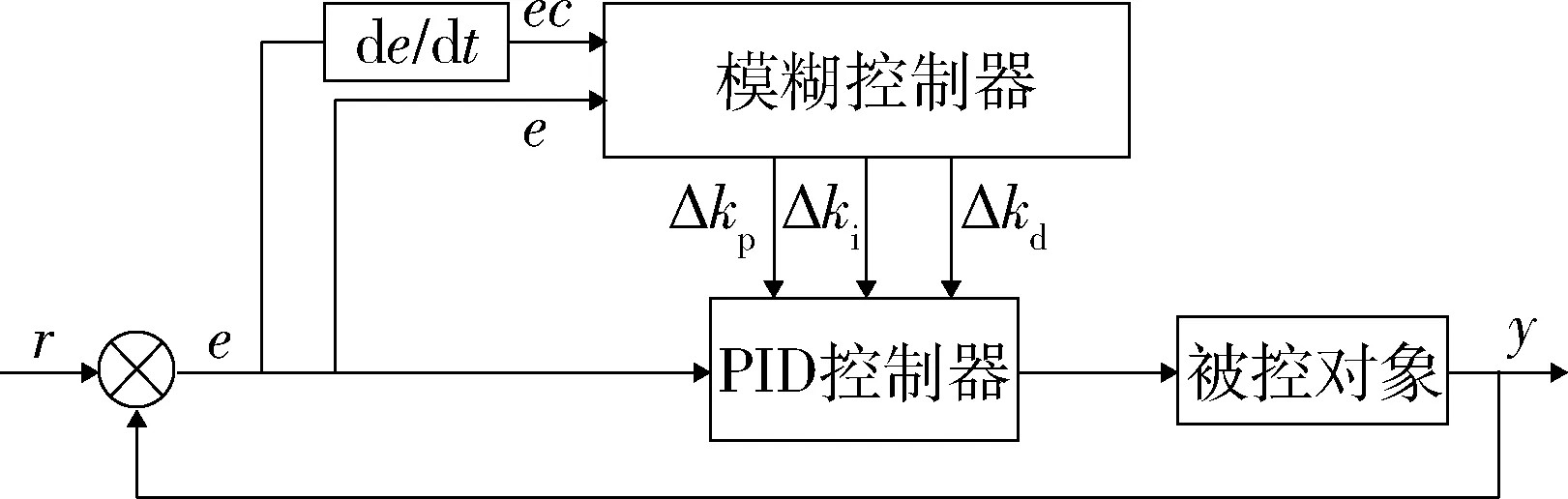
图3 模糊PID控制原理图
Δkp、Δki、Δkd是PID控制的修正量.模糊PID控制的参数按照式(5)计算.
(5)
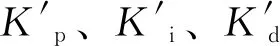
如图4所示,模型主要包括目标信号模块、模糊PID控制策略模块、联合仿真模块和文件储存模块.
图4的联合仿真模块的输出参数为图3联合仿真模块的输入参数.系统将输入到AMEsim的液压缸压力与目标信号模块中的目标压力进行比较,再输入到模糊PID控制策略模块输出电机电压,继而输入到联合仿真模块形成闭环.所有仿真输出信号结果储存到文件储存模块.
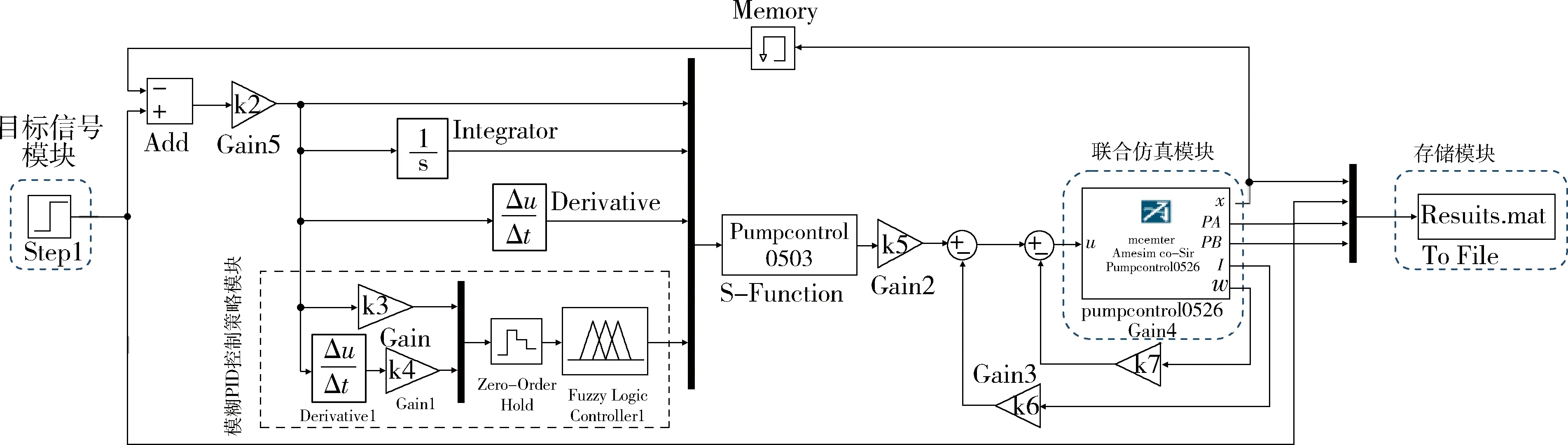
图4 SIMULINK仿真模型图
2 直驱式容积控制系统评估
2.1 系统响应品质因素
直驱式容积控制系统响应品质因素主要包括系统超调量Mp、系统上升时间tr、系统稳定时间ts和系统稳态误差|e|,如图5所示.
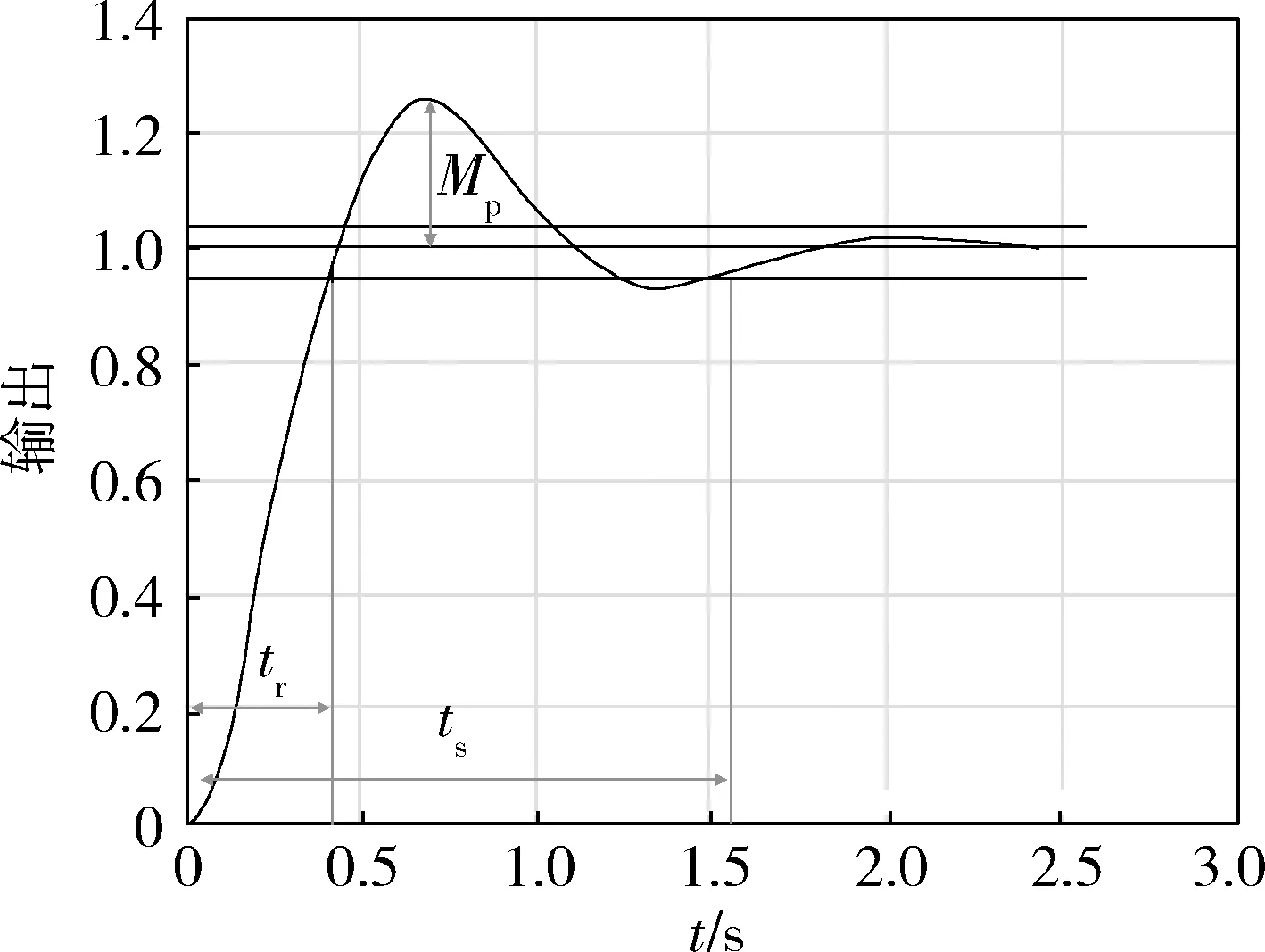
图5 系统品质示意图
系统超调量Mp越大,系统上升时间tr和系统稳定时间ts越小,则表示制动距离越短,制动时间越短.一般情况下,系统上升时间tr越小,系统超调Mp越大,但是超调量过大制动时冲击也越大,容易给驾驶员产生误判.所以需要平衡上升时间和系统超调之间的取值.另外系统稳态误差|e|越小,表明系统越精准,越有助于驾驶员刹车判断.
结合制动系统需求,提出了系统响应品质因素Qm.对系统超调Mp、系统上升时间tr、系统稳定时间ts、系统稳态误差|e|按式(6)进行加权处理.
Qm=α·Mp/Mp′+β·(m·tr/tr′+n·ts/ts′)+γ·|e|/|e|′,
(6)
Mp=(c(tp)-c(t∞))/c(t∞),
(7)
α+β+γ=1,
(8)
m+n=1.
(9)
式中:c(tp)为最大超调值;c(t∞)为稳定时系统值;α、β、γ,m,n为加权系数;Mp′为参考超调量;tr′为参考系统上升时间;ts′为参考系统稳定时间,|e|′为系统参考稳态误差.
当系统都处于参考值时,可发现系统响应品质因子Qm=α+β(m+n)+γ=1.当系统改变参数时,若Qm<1,则表明4个指标参数至少有一个数值下降,且可能权重较高,说明系统响应品质好于参考值;相反若Qm>1,说明系统响应品质下降.
根据制动系统需求,需要尽量缩短制动距离和制动时间,保证系统的安全性,提高系统精度.所以对系统超调量Mp、系统上升时间tr、系统稳定时间ts的权重取值较大,对系统稳态误差权重|e|取值较小,同时在系统上升时间tr和系统稳定时间ts里,制动系统更加关注即时性,所以对系统上升时间tr的权重取值更大.
令α=0.3,β=0.5,γ=0.2,m=0.6,n=0.4,则将权重系数代入式(6)可得式(10).
Qm=0.3Mp/Mp′+0.5(0.6tr/tr′+0.4ts/ts′)+0.2|e|/|e|′.
(10)
2.2 系统敏感因子
有了系统响应品质因子Qm之后,若改变电机转矩系数、液压泵死区体积、液压缸库伦摩擦力和系统泄漏量等系统参数,便可知道参数对系统响应的影响.Qm越大则系统响应品质越差,Qm越小说明系统越优.但是单一Qm,无法观察系统对不同参数改变的敏感程度,所以提出新的观察变量系统敏感因子μ.
(11)
式中:Qm′为参考系统响应品质因子,即Qm′=1;x为待改变的参数值;x′为待改变的参考值.
所以,
(12)
μ越大则说明系统对该参数变化越敏感,在系统变化中属于主要因素.μ越小则说明该参数变化在系统中属于次要因素,只要参数变化不大对系统影响就会较小.
3 直驱式容积控制系统响应特性仿真
3.1 系统参考值

系统参考值仿真结果如图6所示,Mp=334 N,tr=0.34 s,ts=0.75 s,|e|=183 N.
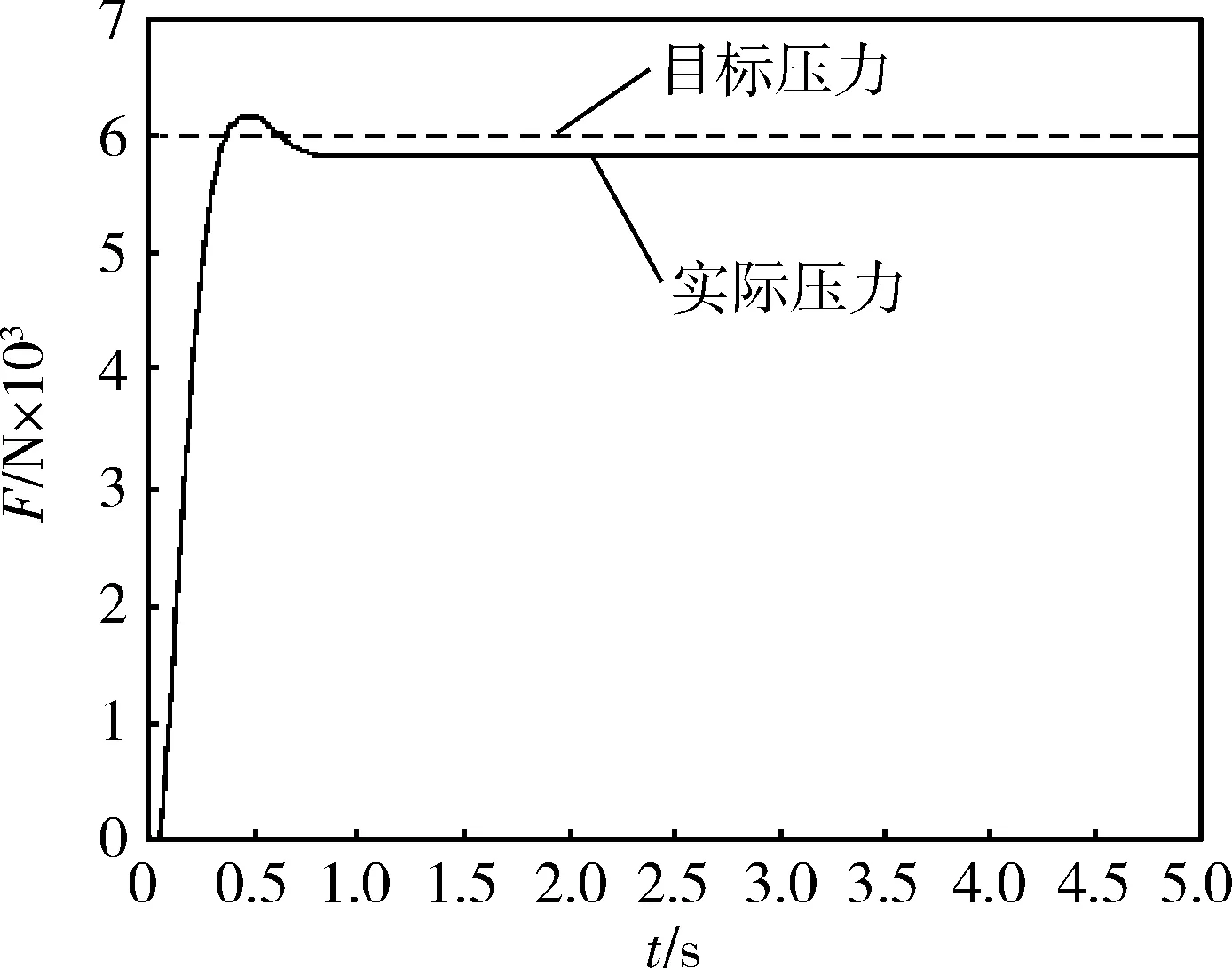
图6 系统初始化参考指标仿真图
3.2 电机转矩系数
系统的电机转矩系数kt分别为1、1.5、2.4、3 V·s/rad时,仿真结果如图7所示.

图7 电机转矩系数kt改变时的系统压力仿真图
当电机转矩系数kt=2.4 V·s/rad时,系统的Mp=0 N,tr=0.63 s,ts=0.63 s,|e|=177 N,此时可根据式(10)和式(12)计算得出:响应品质因素Qm=0.917,敏感因子μ=0.415.
同理,当电机转矩系数为3.0 V·s/rad时,Mp=0 N,tr=0.9 s,ts=0.9 s,|e|=214 N,此时Qm=1.268,μ=0.536.
由图7可知:电机转矩系数的变化,对系统的影响很明显.从响应品质因素来分析,适当地增大电机转矩系数能改善系统的响应,提高制动性能;过度增大电机转矩系数反而会使系统响应变差,制动时间变长,降低了制动性能.而降低了电机转矩系数之后,系统的波动大大增加,超调量变大且系统稳定时间增长,对系统来说响应品质变差.从敏感因子来分析,两次的敏感因子分别为0.415、0.536,均值为0.476,几乎每单位电机转矩系数变化能带动半个单位品质因素变化,体现了系统对电机转矩系数非常敏感.由此可以得到,电机转矩系数改变对系统响应特性影响很大,只要电机转矩系数取2.0~2.4 V·s/rad范围内的任何值,都能够使系统响应品质变得更好.
3.3 液压泵死区体积
液压泵死区体积Vd分别为10、25、100、200 cm3时,仿真结果如图8所示.
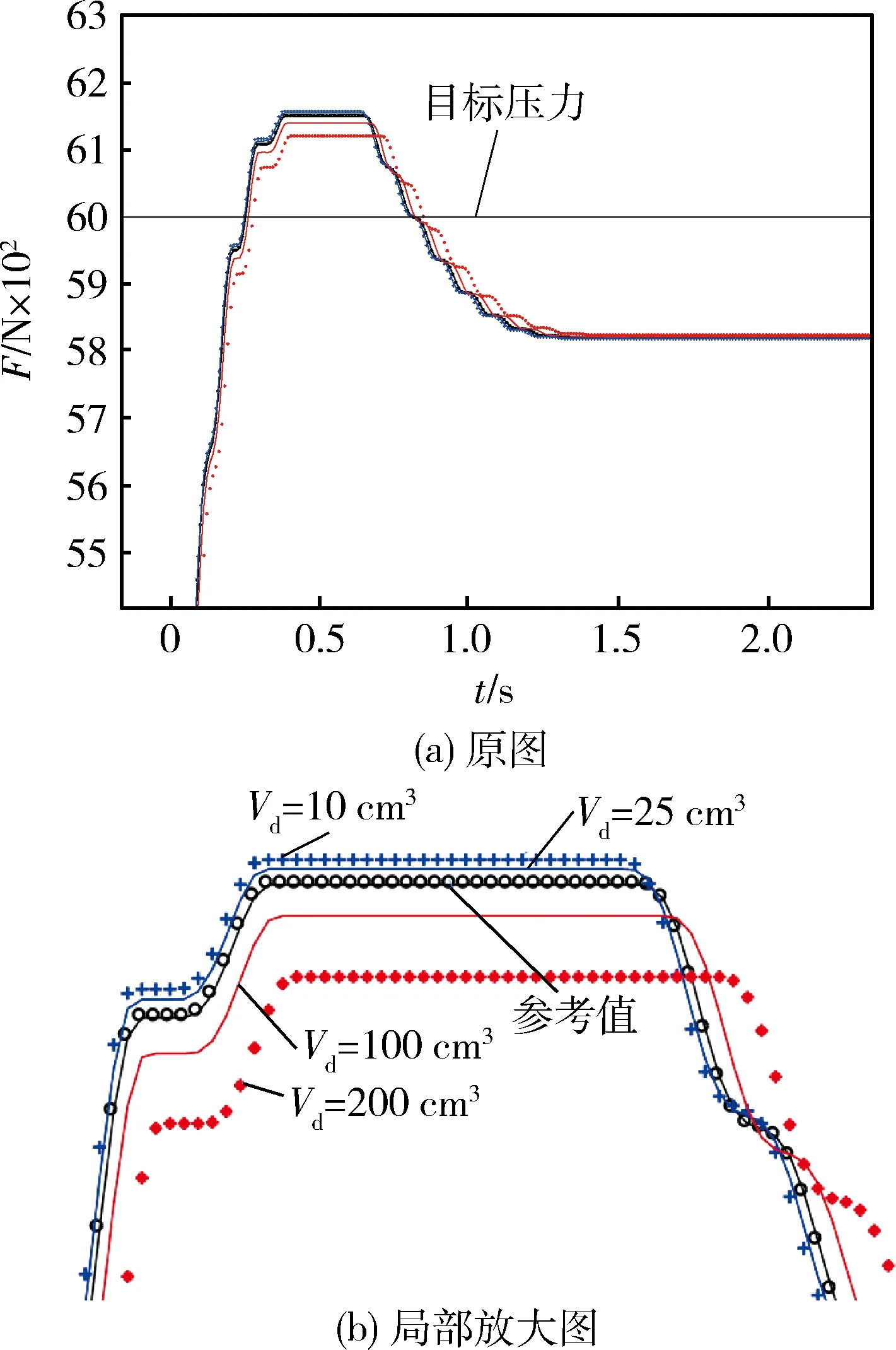
图8 液压泵死区体积Vd改变时的系统压力仿真图
将仿真结果数据代入式(10)和式(12),计算出系统响应品质因素Qm和系统敏感因子μ.如表2所示.
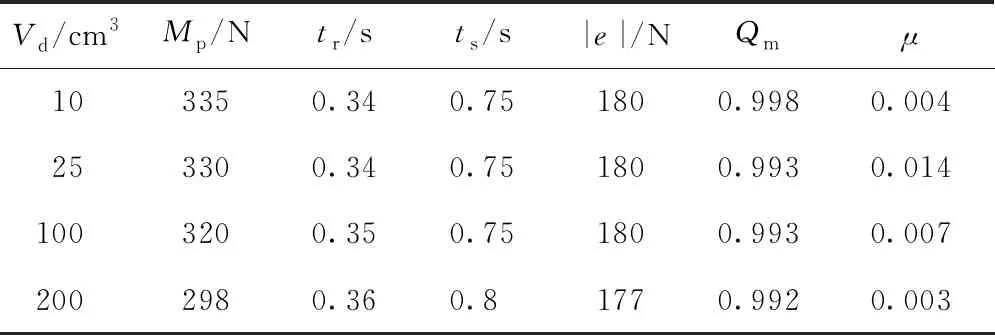
表2 液压泵死区体积改变结果表
由图8和表2可知:改变液压泵死区体积对系统影响不大,无论是超调量、响应时间或者是稳态误差变化都不大.从响应品质因素Qm来看,增大系统液压泵死区体积能稍微提高系统的品质,提高制动稳定性;从敏感因子μ分别为0.004、0.014、0.007和0.003、均值为0.007也可知,液压泵死区体积改变对系统的响应影响较小,与图8仿真结果一致,表明敏感因子设计的合理性.
3.4 液压缸库伦摩擦力
液压缸库伦摩擦力f分别为50、100、400、800 N时,仿真结果如图9所示.

图9 液压缸库伦摩擦力f改变时的系统压力仿真图
将仿真结果数据代入式(10)和式(12),计算出系统响应品质因素Qm和系统敏感因子μ.如表3所示.
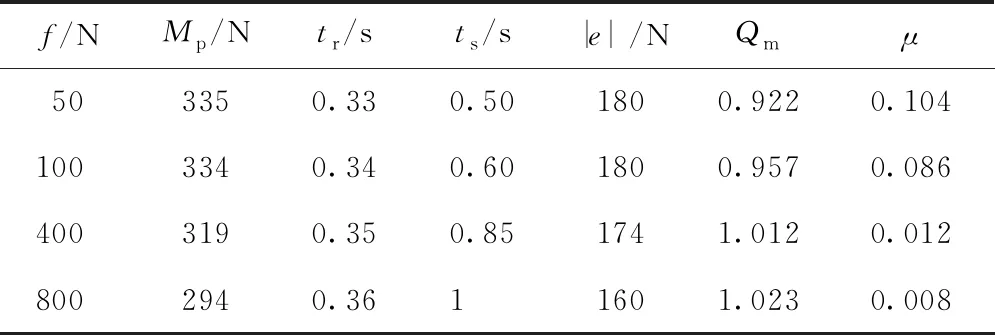
表3 液压缸库伦摩擦力改变结果表
由图9和表3可知:增大液压缸的库伦摩擦力,会略微降低系统超调量和稳态误差;提高系统响应时间,会造成制动时间增加.从响应品质因素Qm分别为0.922、0.957、1.012和1.023可看出,增大库伦摩擦力会稍微降低系统的品质,也会造成制动性能下降.从敏感因子μ均值为0.0525可知,系统响应对液压缸库伦摩擦力的改变敏感性较低.
3.5 系统泄漏量
系统泄漏量λ分别为0.002、0.005、0.02、0.04 L/min/Mpa时,仿真结果如图10所示.

图10 系统泄漏量λ改变时的系统压力仿真图
将仿真结果数据代入式(10)和式(12),计算出系统响应品质因素Qm和系统敏感因子μ.如表4所示.

表4 系统泄漏量改变结果表
由图10和表4可知,系统泄漏量对系统最大的影响是系统稳态误差.系统泄漏量增加稳态误差也大大增加,另外系统泄漏量增大会略微降低系统超调,对响应时间的影响非常小.系统响应品质因素Qm在系统泄漏量增加时增大,说明系统泄漏量越大系统响应越差,即制动性能下降.从敏感因子μ均值为0.144来看,系统对系统泄漏量的变化较为敏感,所以需严格控制系统的泄漏情况.系统泄漏量增大,制动距离增加.当系统泄漏量小于0.005 L/min/MPa时,能使系统响应特性变好.
4 结 论
为研究直驱式容积控制系统应用于车辆制动的情况,搭建了基于AMEsim和Simulink联合仿真的直驱式容积模糊PID控制压力模型.
仿真结果表明,适当增大电机转矩系数能有效提高系统响应品质,降低制动超调,方便驾驶员判断制动反馈情况;增大液压泵死区体积也能稍微提升系统响应品质,降低了系统超调和稳态误差,使制动更加稳定;增大液压缸库伦摩擦会降低系统响应品质,使系统稳定时间增加,制动时间增加;增大泄漏量,会大大降低系统响应品质,系统稳态误差过大,会导致实际制动力达不到目标需求制动力,制动距离会增加.通过系统品质因素,优化了系统参数选择,系统电机转矩系数在2.0~2.4 V·s/rad范围内、泄漏量小于0.005 L/min/MPa时会有较好的系统响应.
通过敏感因子发现,电机转矩系数和系统泄漏量改变对系统的影响程度更大,液压缸死区体积和液压缸库伦摩擦改变对系统影响较低.通过仿真结果也能够印证系统响应品质因素和敏感因子设计的合理性,能够帮助判断不同系统影响参数改变时对制动系统的作动影响.
