基于离网型逆变器的输出阻抗重塑方法研究

周书颖，洪冬颖，陈翔，韩鹏，云阳，王凯，耿乙文

(1. 中国矿业大学 a.信息与控制工程学院；b.电气与动力工程学院，江苏 徐州 221008；2. 国电南瑞科技股份有限公司南瑞研究院，江苏 南京 211106)

近年来，能源需求量不断增加，环境问题日益严重[1-4]，基于可再生能源的分布式发电系统(如光伏发电、风力发电、燃料电池等)正在快速发展。当主电网发生故障时，分布式发电单元必须马上退出运行，这就限制了分布式发电充分发挥其性能[5]。微电网技术可以更好地促进大规模分布式发电的整合和应用，因此得到广泛关注[6-8]。微电网可以运行在并网模式和离网模式下，一般采用电压源型逆变器作为电网与本地负载的接口。

微电网工作在离网模式时，由于大量非线性负载的接入，负载电流会对逆变器输出电压产生影响[8-10]，使系统不满足运行要求[11-13]。负载电流中的谐波会导致逆变器输出电压中谐波含量增大，谐波抑制技术在并网逆变器系统中已相当成熟[14-15]，而在离网逆变器系统中还处于初始阶段[16-17]；除此之外，随着负载电流的增加，逆变器输出电压跌落越来越严重。因此，研究如何抑制谐波负载导致的逆变器输出电压畸变以及负载电流较大引起的逆变器输出电压跌落势在必行。文献[18]采用负载电流比例前馈来抑制负载电流对电压的干扰，该方法在电流中只含有5次以下谐波时有一定的效果，而在含有较高次谐波时误差较大。文献[16]采用多比例谐振(multi-proportion-resonant，MPR)控制器，分别对各次谐波进行抑制，达到了较好的效果；但是MPR控制器算法复杂，计算量大，在高开关频率场合无法实现。文献[19]在文献[16]的基础上加入了虚拟负序阻抗环，抑制不平衡产生的负序电流。对于逆变器输出电压的跌落问题，文献[10]通过框图化简，将负载电流移到电压调节器后面，分析输出与输入的关系，并采用前馈来抑制负载电流扰动；但是前馈项中含有比例项、一阶微分项、二阶微分项，而高阶微分会引入高频干扰。文献[20]根据文献[13]的分析，对比了比例前馈、比例加一阶微分前馈与全前馈的区别，通过忽略二阶微分项来抑制电压跌落，并采用向后差分代替一阶微分；但是当开关频率较低时，该方法存在较大误差。

鉴于以上分析，本文建立了离网型逆变器的阻抗模型，从输出阻抗的角度出发，分析负载电流对逆变器输出电压的影响。比例谐振(proportion-resonant，PR)控制器可以对正弦量无静差控制，采用多谐振控制器可以补偿各次谐波，但是设计复杂，计算量大，产生很大的计算延时。文献[21]提出旋转坐标系下的降阶谐振控制器，但并未分析其机理，而且需要进行坐标变换。本文通过模型降阶，得到静止坐标系下的比例降阶多谐振(proportion and reduced-order multi-resonant，PROMR)控制器，不需要进行坐标变换，实现简单，计算量小，可以对各次谐波进行抑制，并采用负载电流低通正交前馈(load current low-pass quadrature feedforward，LCLPQF)控制策略进一步抑制输出电压的跌落。最后通过仿真和实验，对本文所提出的静止坐标系下“PROMR控制器+LCLPQF策略”的阻抗重塑方法的有效性进行验证。

1 离网型逆变器阻抗模型

三相离网型逆变器的主电路拓扑如图1所示，其中，C为直流侧滤波电容，Z为负载，ij和ioj(j=a,b,c，代表A、B、C三相)分别为变换器侧电流和负载电流，L、R、Cf分别为LC滤波器的滤波电感、滤波电感等效电阻和滤波电容，Idc、Udc分别为直流侧电流和电压。两相静止坐标系下的LC滤波器数学模型如图2所示，其中，I1(s)为电感电流，Io(s)为输出电流，Ic(s)为电容电流，Uc(s)为电容电压，U(s)为电压源电压。

图1 LC滤波的三相离网型逆变器主电路拓扑Fig.1 The main circuit topology of LC-typed three phase off-grid inverter

图2 两相静止坐标系下的LC滤波器数学模型Fig.2 Mathematical model of LC filter in the two-phase stationary frame

根据两相静止坐标系下LC滤波器的数学模型，由基尔霍夫电压电流定律，可得其数学表达式为：

(1)

式中：ZL(s)为滤波电感的阻抗，ZL(s)=sL+R，s为拉普拉斯变换的复变量；YCf(s)为滤波电容的导纳，YCf(s)=sCf。

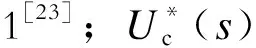
图3 离网型逆变器的控制框图Fig.3 Control diagram of off-grid inverter

TD(s)为等效延时环节，将1个采样周期的时间延迟进行帕德近似，得到的等效延迟传递函数为[25]

(2)

式中Ts为逆变器中开关管的开关周期。

由图3可得：

(3)

式中Fm(s)为时延函数。

结合式(3)和式(1)，可得离网型逆变器输出电压复传递函数表达式为

(4)

式中：Gv(s)为电压闭环增益；Zo(s)为闭环输出阻抗。

(5)

(6)

其中，

A(s)=GPR(s)kFm(s)+1-Fm(s)，

(7)

B(s)=(ZL(s)+kFm(s))YCf(s).

(8)

从式(4)可以看出，逆变器输出电压由2个部分组成：第1项等效为受控电压源，为输出电压的主要分量；第2项为扰动分量，输出电流经闭环输出阻抗Zo(s)产生。根据戴维南定理，可得离网型逆变器的阻抗模型如图4所示。

图4 离网型逆变器的阻抗模型Fig.4 Impedance model of off-grid inverter

由式(4)和图4可知，由于逆变器输出阻抗的存在，负载电流必然会在阻抗上产生压降，如果阻抗较大，该影响不可忽略，一方面使输出电压畸变，另一方面导致输出电压跌落。当采用PR控制器时，逆变器输出阻抗伯德图如图5所示。从逆变器输出阻抗频率特性可以发现：采用PR控制时，逆变器输出阻抗在低频段和中频段较大，当负载电流中含有5、7、11、13次谐波时，输出电压中无疑会产生5、7、11、13次谐波，使逆变器输出电压畸变；当输出电流较大时，还会在逆变器等效输出阻抗上产生很大的压降，使公共连接点处电压跌落，系统不满足运行要求。因此，必须进行优化控制。

图5 基于PR控制器的逆变器输出阻抗伯德图Fig.5 Bode plot of inverter output impedance based on PR controller

2 阻抗重塑策略

2.1 基于MPR的阻抗重塑

根据以上分析可知，逆变器输出阻抗的存在，会引入负载电流干扰。MPR控制器可以实现对各次谐波的抑制，其数学表达式为

GMPR(s)=kP+G1(s)++G5(s)+G7(s)+

G11(s)+G13(s).

(9)

各次谐振控制器表达式为：

(10)

式(9)、(10)中：kP为电压环比例系数；krq(q=1，5，7，11，13表示各次谐波)为电压环谐振增益；ωq为各次谐波的角频率；ωb为带宽，实际系统中频率会有波动，加入一定的带宽可以使系统在较宽频带内获得较高增益[26]。根据式(9)得到MPR控制器频率特性如图6所示。可以看出，在各次谐波处MPR控制器增益很大，从而实现对各次谐波的抑制。采用MPR控制器后，三相离网型逆变器控制框图如图7所示。

图6 MPR控制器伯德图Fig.6 Bode plot of MPR controller

图7 基于MPR控制器的离网型逆变器控制框图Fig.7 Control diagram of off-grid inverter based on MPR controller

MPR控制器之所以可以实现对非线性负载电流扰动的抑制，除了高开环增益外，另一方面是因为采用MPR控制器后，逆变器输出阻抗得到重塑。将式(9)代入式(6)，得到采用MPR控制器的阻抗频率特性如图8所示。

图8 基于MPR控制器的逆变器输出阻抗伯德图Fig.8 Bode plot of inverter output impedance based on MPR controller

对比图5和图8可以看出，采用MPR控制器后，5、7、11、13次谐波频率处阻抗得到极大衰减，当负载电流中含有5、7、11、13次谐波电流时，经过逆变器输出阻抗产生的谐波电压很小，可以忽略，因此MPR控制器可以对谐波电压进行抑制。然而MPR控制器传递函数为二阶，数字控制器处理时需要大量的计算时间，当含有较多谐振控制器时，不利于数字控制器的实现。

根据以上分析可知，MPR控制器可以对输出阻抗进行重塑，很好地抑制谐波电流对输出电压的影响，但是计算量较大，不适合在高开关频率和离网型逆变器中使用。如果能对MPR控制器进行降阶，简化计算，使数字控制器能够快速实现，那么MPR控制器就具有更宽的应用领域。

2.2 PROMR控制器设计

针对MPR控制器存在计算时间长的问题，本节主要研究MPR控制器的降阶，减少数字控制器的计算时间。由PR控制器机理可知，静止坐标系下的PR控制器与旋转坐标系下PI控制器本质上一致[27]，将旋转坐标系下的PI控制器转换到静止坐标系下可得[28]：

(11)

(12)

为适应频率波动，式(12)中加入一定的带宽，表达式变为

(13)

将式(13)代入式(11)展开，暂不考虑比例项，化简可得正序分量

(14)

其中，

(15)

同理可得负序分量

(16)

从式(14)、(16)可以看出，式中只含有s的一次项，实现了谐振控制器的降阶，其控制框图如图9所示。

图9 降阶谐振控制器的控制框图Fig.9 Control diagram of reduced-order resonant controller

从图9可以看出，要实现其他次谐波的阻抗重塑，只需更改ω即可，大大简化了多谐振控制器的实现方式，减少了计算时间，并且控制参数与MPR控制器一致，避免了重新进行参数设计。

综上，可得PROMR控制器数学表达式为:

(17)

2.3 LCLPQF策略

采用多谐振控制器，逆变器输出阻抗得到重塑。由图8可知，5、7、11、13次谐波频率处阻抗极大地衰减，谐波阻抗很小，因此负载电流中谐波电流的干扰得到抑制。但是当功率较大时，基波电流含量较高，为了使PR控制器在较宽频率带内获得高增益，50 Hz处逆变器输出阻抗并非无穷小，因此基波电流扰动无法完全抑制，会使逆变器输出电压跌落，并且基波电流扰动会随着功率的增加而增大。结合图2和图3，可以得到离网型逆变器的系统控制框图如图10所示，其中GQ(s)为前馈函数，IQ(s)为前馈电流。

图10 离网型逆变器的系统控制框图Fig.10 System control diagram of off-grid inverter

由图10可知，为了抑制负载电流的扰动，可以在电流调节器输出端加入电流前馈。当前馈项

(18)

时，通过框图化简可以得到闭环传递函数

(19)

由式(19)可知，采用全前馈后，逆变器输出电压只与闭环增益有关，扰动项被消除，可以完全抵消负载电流扰动，这样输出电压不再受负载电流的影响。然而，式(18)中含有微分环节和超前环节，该前馈项可能无法实现。由以上分析可知，采用多谐振控制器后，只需对基波阻抗进行重塑，就可以抑制电压跌落。TD(s)频率特性如图11所示，在低频处幅值为1。

图11 TD(s)伯德图Fig.11 Bode plot of TD(s)

因此，可以采用低通滤波器进行滤波，再采用正交前馈即可实现低频全前馈，重塑基波阻抗，前馈电流的α轴、β轴分量分别为：

(20)

(21)

式(20)、(21)中：Iα1(s)、Iβ1(s)分别为一次谐波对应的α轴、β轴电流；l(s)为低通滤波器传递函数；ωc为低通滤波器的截止频率。

采用LCLPQF策略后闭环输出阻抗复传递函数

(22)

根据式(22)，得到采用LCLPQF策略的逆变器输出阻抗伯德图如图12所示。可以看出，加入LCLPQF策略后基波频率附近阻抗非常低，50 Hz以下阻抗也得到降低，还可以抑制负载电流中低频分量引起的低频振荡。

图12 基于“PROMR控制器+LCLPQF策略”的逆变器输出阻抗伯德图Fig.12 Bode plot of inverter output impedance based on PROMR+LCLPQF

3 实验验证

为了验证“PROMR控制器+LCLPQF策略”的阻抗重塑方法的有效性，在三相10 kW离网型逆变器平台上进行实验研究，实验参数见表1。

表1 系统参数Tab.1 System parameters

控制板采用TI公司的TMS320F28335型数字信号处理器(digital signal process，DSP)作为控制器，Xilinx公司的XC3S400型现场可编程门阵列(field programmable gate array，FPGA)作为外围辅助控制器，完成脉冲输出、AD/DA采样及故障保护功能。

为了验证负载对输出电压的影响，图13分别给出了空载和带载时三相输出电压波形及A相电压频谱分析。

图13 采用PR控制器时的空载及带载输出电压Fig.13 Waveform of no-load and load based on PR controller

由图13(a)、(b)可以看出，因为不受负载影响，空载时三相输出电压波形电能质量较高。由图13(c)、(d)可以看出，当接入谐波负载后，输出电压畸变严重，其中5、7、11、13次谐波含量较高；因此，本文只加入5、7、11、13次谐振控制器，对5、7、11、13次谐波进行抑制。图14中(a)、(b)分别为采用MPR控制器时三相输出电压波形及A相电压频谱分析，图15中(a)、(b)分别为采用PROMR控制器时三相输出电压波形及A相电压频谱分析。对比PR与MPR控制时的三相电压及其频谱分析可以发现，加入5、7、11、13次谐振调节器后，总谐波畸变率由6%降到1.2%，谐波抑制效果明显。对比MPR与PROMR控制时的三相电压及其频谱分析可以看出，采用PROMR控制时效果与MPR控制时效果一样，验证了PROMR控制器的有效性。

图14 采用MPR控制器时的输出电压Fig.14 Output voltage waveforms using MPR controller

为了验证LCLPQF策略的有效性，图16、图17分别给出了无LCLPQF策略和有LCLPQF策略时的逆变器三相输出电压动态波形，t1时刻突加负载，t2时刻稳定运行。其中，ua为A相输出电压，ia为A相输出电流，Δua为A相输出电压的差值。

图15 采用PROMR控制器时的输出电压Fig.15 Output voltage waveforms using PROMR controller

图16 无LCLPQF策略的实验波形Fig.16 Experimental waveforms without LCLPQF

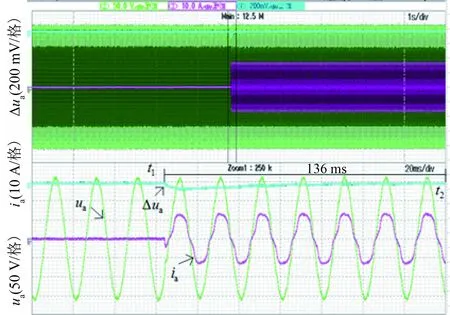
图17 采用LCLPQF策略的实验波形Fig.17 Experimental waveforms with LCLPQF

对比图16和图17可以发现：无LCLPQF策略时，负载突变瞬间电压跌落较为严重；采用LCLPQF策略后，负载突变瞬间电压跌落减小50%，并且恢复时间缩短了2.5个工频周期。加入负载，稳态运行时，无LCLPQF策略时输出电压跌落了5 V，采用LCLPQF策略后输出电压保持不变，验证了LCLPQF策略的有效性。

4 结束语

本文针对离网型逆变器接入非线性负载时，谐波电流对逆变器输出电压造成干扰的问题进行研究。建立离网型逆变器阻抗模型，从输出阻抗的角度分析，发现输出电压由2个部分组成：一部分由电压指令值经闭环增益得到；另一部分为扰动分量，由负载电流经闭环输出阻抗产生。由于扰动分量的存在：①谐波电流经过闭环输出阻抗引入谐波电压，使输出电压畸变；②功率增大时，基波电流经闭环输出阻抗产生较大压降，使输出电压跌落。实验结果表明，本文提出的基于静止坐标系下“PROMR控制器+LCLPQF策略”的阻抗重塑方法，改善了输出电压波形，抑制了输出电压跌落，该结果也体现了算法的有效性与优越性。这一阻抗重塑方法能否推广到并网逆变器还需要进行进一步的研究。